| 光电延迟反馈系统几种混沌路径的仿真分析 |
19世纪末20世纪初提出的庞加莱映射方法对非线性动力学理论的发展有重大贡献,直至1963年洛伦兹提出的蝴蝶效应对非线性动力学理论复兴起着重要作用.20世纪七十年代这种非线性动力学领域才被广泛的推广认知,并命名为“混沌理论”.在这新兴科学领域里人们从现实世界中找到各种混沌现象.特别在光学领域,上世纪70年代末,在Ikeda环腔的开创性研究,相关非线性光学系统的动力特性的分析成为研究热点之一[1, 2].
当额外的激光注入到半导体激光器会出现不稳定现象.光反馈或注入外部光源到激光器可以产生不稳定或混沌脉冲.与这些激光器相比,光电震荡系统更可靠和灵活,且由于反馈回路使其是无限维系统.由于光电震荡系统的复杂动力特性,在混沌保密通信、混沌雷达、储备池计算等领域有重 要的应用前景[5, 6, 7, 15].
产生混沌激光的光电时滞反馈震荡系统框图如图 1所示.系统中激光二极管(LD)稳定工作在连续光输出模式,输出光功率为P,经过偏振控制器(PC)输入到马赫-增德尔调制器(MZM),其直流输入半波电压和射频输入半波电压分别为vπDC和vπRF.马赫-增德尔调制器的非线性调制输出光强经过一定长度光纤,延迟τ时间后,输入到宽带光电探测器(PD),将光信号转化成电信号.电信号再通过带通滤波器(BPF)后经射频放大器放大后输入到MZM的射频调制端,实现延迟反馈.系统中,MZM的直流偏置电压为vB,射频调制端的输入电压为v(t);BPF的高频和低频截止频率分别为wh和wl;反馈环中的总的衰减和增益分别表示为α和G.
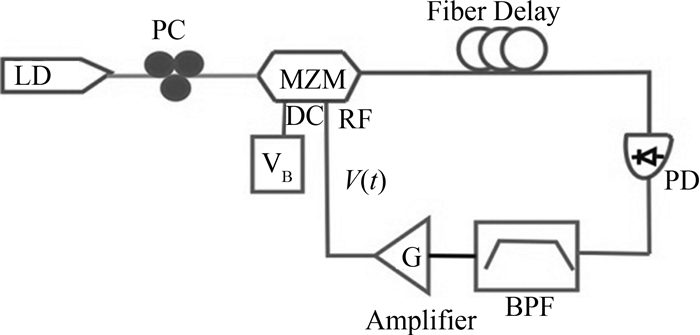 |
| 图1 光电延迟反馈系统结构示意图 Fig. 1 Structure of an optoelectronic delay feedback system |
本文通过数值分析的方法研究光电延迟反馈震荡系统产生混沌信号的过程,详细分析模型中直流偏置电压和反馈增益对系统动力特性的影响.
1 数学模型和计算方法为了探究光电反馈震荡系统的动力特性,建立其数学模型.
系统中的带通滤波器对系统产生丰富的动力特性起着重要作用.频域内二阶带通滤波器的传输函数H(w)可表示为
| $ H\left( w \right) = \frac{{j{w_{\rm{h}}}w}}{{\left( {{w_{\rm{h}}} + jw} \right)\left( {{w_1} + jw} \right)}} = \frac{{U\left( {jw} \right)}}{{P\left( {jw} \right)}}, $ | (1) |
式中,U(jw)=V(jw)/G和P(jw)分别是带通滤波器的输出信号u(t)和输入信号p(t)的傅里叶变换.MZM是光电震荡器中实现光功率的非线性(cos2)传递,是核心器件.带通滤波器的输入信号p(t)是马赫-增德尔调制器输出端的光强通过光纤延迟τ时间后进行光电转换,
| $ p\left( t \right) = \alpha P{\cos ^2}\left[{\frac{{\pi v\left( {t - \tau } \right)}}{{2{v_{\pi {\rm{RF}}}}}} + \phi } \right],$ | (2) |
式中,Φ由MZM直流偏置电压vB调节.电压v(t)=FT-1[V(jw)]是MZM的射频输入电压,等于带通滤波器输出电压u(t)的G倍放大,即Gu(t).假设系统中的光电探测器和射频放大器的频带都超出带通滤波器,即带通滤波器的输出信号u(t)再没有被其它器件滤波.
用傅里叶反变换规则[jw→d/(dt),(jw)-1→∫dt],将式(1)从频域转换成时域方程式,可得
| $ \begin{array}{l} {w_1}\int_{{t_0}}^t {v\left( s \right){\rm{d}}s + v\left( t \right)\left( {1 + \frac{{{w_1}}}{{{w_{\rm{h}}}}}} \right) + \frac{1}{{{w_{\rm{h}}}}}v'\left( t \right)} = \\ G\alpha P{\cos ^2}\left[{\frac{{\pi v\left( {t - \tau } \right)}}{{2{v_{\pi {\rm{RF}}}}}} + \phi } \right]. \end{array}$ | (3) |
系统带通滤波器wh和wl分别在GHz和kHz数量级上,因此式(3)中wl/wh可忽略不计.设x(t)=πv(t)/2vπRF,代入式(3)得式(4),x(t)作为输出信号来研究光电延迟反馈系统输出的动态特性.
| $ \begin{array}{l} {w_1}\int_{{t_0}}^t {v\left( s \right){\rm{d}}s + x\left( t \right) + \frac{1}{{{w_{\rm{h}}}}}v'\left( t \right)} = \\ \beta {\cos ^2}\left[{x\left( {t - \tau } \right) + \phi } \right], \end{array}$ | (4) |
式中归一化参数β=παPG/2VπRF为系统延迟反馈增益,可通过输入激光光强P来调节.相位偏置Φ=πvB/2vπDC,由直流偏置电压控制,周期为π的参数.延迟反馈增益和相位偏置是决定系统的动力特性的两个关键参数[3].
为便于求解分析,设y=∫x(s)ds,可将光电延迟反馈震荡系统的非线性二阶延迟微分方程式(4)写成
| $ y'\left( t \right) = x\left( t \right),w_{\rm{h}}^{ - 1}x'\left( t \right) = \beta {\cos ^2}\left[{x\left( {t - \tau } \right) + \phi } \right] - x\left( t \right) - {w_1}y\left( t \right). $ | (5) |
系统中固定参数取值和含义见表 1.
| 表1 光电延迟反馈系统模型参数 Table 1 Parameters of optoelectronic delay feedback system |
 |
| 点击放大 |
光电延迟反馈系统的数学模型为延迟微分方程,即某一时刻t系统的数值解与系统在t时刻及t-τ时刻的数值解都有关.本文采用工程上广泛应用的高精度算法龙格-库塔(Runge-Kutta)方法,数值求解延迟微分方程.龙格-库塔法是一种微分方程近似求解的数值方法.通过计算不同点上的函数值,并对这些函数值作线性组合,构成近似公式,并使近似公式的局部截断误差阶数尽可能高.四阶龙格-库塔法即其截断误差为O(h5),每步要计算4次函数的值,
| $ \begin{array}{l} {x_i}\left( {t + h} \right) = {x_i}\left( t \right) + h\left( {\frac{1}{6}{k_{1,i}} + \frac{1}{3}{k_{2,i}} + \frac{1}{3}{k_{3,i}} + \frac{1}{6}{k_{4,i}}} \right),i = 1,2,\\ {k_{1,i}} = {f_i}\left( {t,{x_i}\left( t \right),{x_i}\left( {t - \tau } \right)} \right),\\ {k_{2,i}} = {f_i}\left( {t + \frac{h}{2},{x_i}\left( t \right) + h\frac{{{k_{1,i}}}}{2},{x_i}\left( {t + \frac{{h{k_{1,i}}}}{2} - \tau } \right)} \right),\\ {k_{3,i}} = {f_i}\left( {t + \frac{h}{2},{x_i}\left( t \right) + h\frac{{{k_{2,i}}}}{2},{x_i}\left( {t + \frac{{h{k_{2,i}}}}{2} - \tau } \right)} \right),\\ {k_{4,i}} = {f_i}\left( {t + h,{x_i}\left( t \right) + h{k_{3,i}},{x_i}\left( {t + \frac{{h{k_{3,i}}}}{2} - \tau } \right)} \right), \end{array} $ | (6) |
系统中带通滤波器在频域覆盖六个数量级的频谱宽度,其低频截止频率在kHz数量级上,高频截止频率在GHz数量级上.从而假设1/wh→0,动力方程(5)可写成x(t)=βcos2[x(t-τ)+Φ],其特性曲线如图 2所示,可看出在不同的工作点处曲线的切线斜率和非线性程度差异较大,导致系统输出动态也存在较大差异.系统固定点xF在特性曲线x(t)=fNL[x(t-τ)]和直线x(t)=x(t-τ)的交叉点上.随着β的增加,其交叉点的个数也增加.这些固定点的稳定性由固定点在非线性方程上的斜率决定,即βsin[2(xF+Φ0)]:其值小于1时,是稳定的固定点;相反则是不稳定的固定点.从图 2中可看出,稳定的固定点一般在非线性曲线的极值附近.稳定的固定点会随着反馈增益β的增大而变得不稳定.偏置Φ的取值则会取在-π/2,π/2范围内[11].
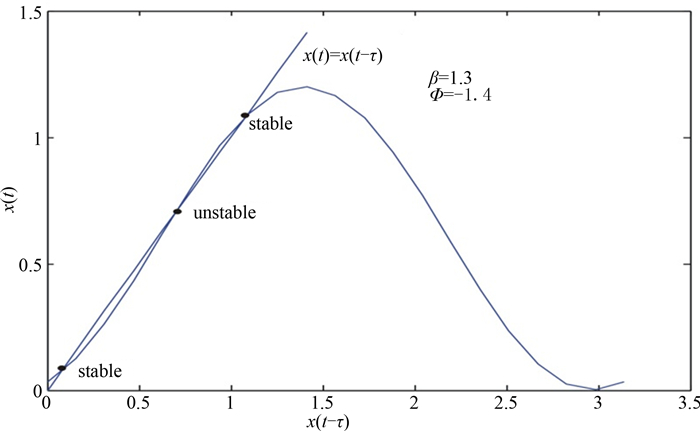 |
| 图2 MZM传输特性曲线 Fig. 2 Transmission curve of MZM |
光电延迟反馈系统以MZM非线性器件为核心,通过调节直流偏置电压选定工作点的情况下,增加反馈增益可以使反馈电压覆盖更大的相位调节范围,导致MZM非线性工作区域增加,使光电延迟反馈系统的输出信号渐入混沌状态.根据图 2曲线中斜率符号的不同,有两种渐入混沌状态的路径[12, 13, 14].
当Φ=-0.78时,系统工作在MZM特性曲线的正斜率区间内,此时光电延迟反馈系统的输出动态时间序列波形如图 3所示.图 3中显示Φ=-0.78时光电延迟反馈系统输出随反馈增益增加进入混沌状态.当β小于1时系统稳定输出;增加反馈增益到大于1时,光电延迟反馈系统的输出为一倍周期状态,见图 3(a)为β=1.5时的波形.从时间序列波形看,图 3(a)中表现出固定周期的震荡,由于周期较长,称为慢速周期震荡[10].β=1.8时,由图 3(b)可发现,光电延迟反馈系统输出在慢速周期震荡的分岔状态上,慢速周期震荡时间序列的上下极值处出现密集的震荡行为,出现文献[9]中发现的“breather”现象.β增加到2.5时,慢速震荡周期依然存在,但在慢速震荡极值处的震荡经过倍周期分岔后已变为混沌状态,显现混沌“breather”现象,时间序列波形图见图 3(c)所示.继续增加反馈增益到3.5时,光电延迟反馈震荡系统的输出为完全混沌状态,如图 3(d)所示.时间序列上已经没有慢速周期震荡了,表现出不规则的复杂震荡.系统在正斜率工作时,随着反馈增益的增加,系统输出会从一倍周期到“breather”现象,再到混沌状态.
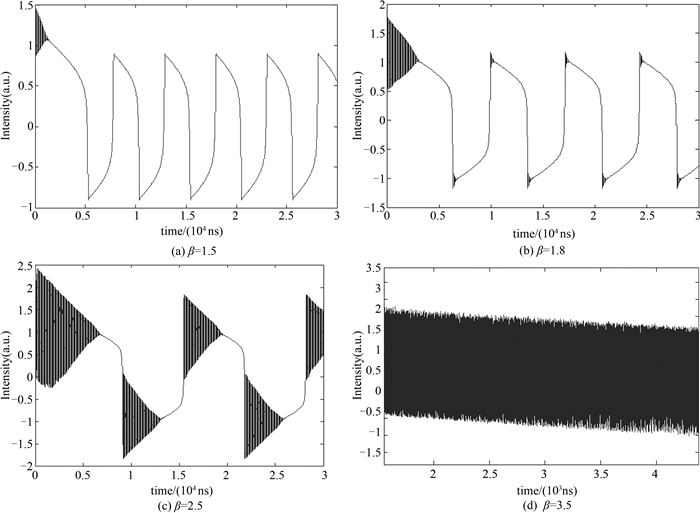 |
| 图3 工作点在正斜率时不同反馈强度下的输出波形 Fig. 3 Output waveform under different feedback gain in positive slope |
Φ=0.78时,MZM的工作点在传输特性曲线的负斜率区间内,其不同状态的时间序列图如图 4所示,表现出随着反馈增益的增加其系统输出进入混沌状态的动态过程.同样β <1时,系统稳定输出.β=1.5时,系统输出为一周期方波,其周期为系统延迟时间τ的两倍,见图 4(a).β增加到2.1时,一周期方波震荡幅度在两个值附近波动,周期不变,如图 4(b)所示.β再增加到2.2时,在方波的基础上出现快速震荡成分,类似于高次谐波分岔,时间序列的快速震荡非常密集,且震荡幅度在两个值附近波动,如图 4(c)所示.继续增加至β=3.5时,系统输出时间序列出现不可预测的振荡幅度,变得更加复杂,进入混沌状态,如图 4(d)所示.
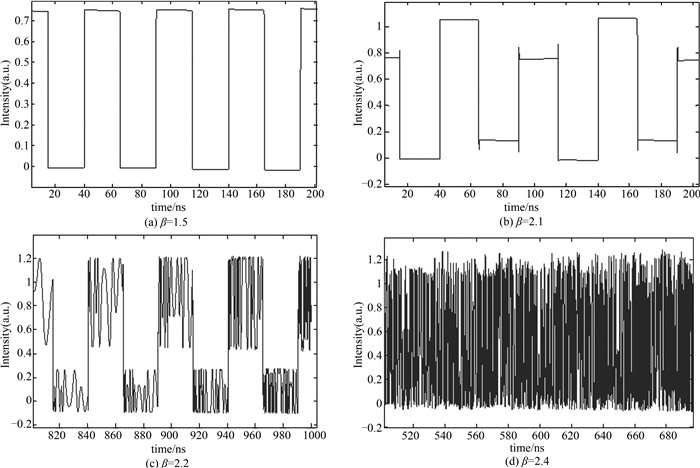 |
| 图4 工作点在负斜率时不同反馈强度下的输出波形 Fig. 4 Output waveform under different feedback gain in negative slope |
研究了非线性光电延迟反馈系统的动力特性,仿真分析出系统输出信号渐入混沌状态的两种不同路径.系统的动态响应可由非线性二阶时滞微分方程表示.通过调节系统中两个重要参数,即反馈增益β和非线性工作点偏置Φ,数值仿真出多种动态时序波形,如:慢速周期震荡、快速方波震荡、规则“breather”、混沌“breather”、不规则复杂震荡、完全混沌等.其中很多新特性的时间序列波形在只有低频截止频率的经典一阶非线性时滞微分方程中是没有的.这种超宽带非线性光电延迟反馈系统的多种动态输出特性满足了众多需要多种光脉冲源的应用[8].
| [1] | WIGGINS, STEPHEN. Introduction to applied nonlinear dynamical systems and chaos[M]. Springer Science & Business Media, 2003. |
| [2] | STEWART H B, THOMPSON J M T. Nonlinear dynamics and chaos[M]. John Wiley & Sons, 2002. |
| [3] | GREGHOTH. The dynamics of delay coupled optoelectronic devices[D]. The Division of Mathematics and Natural Sciences Reed College, 2010:3-12. |
| [4] | ERNEUX, THOMAS. Applied delay differential equations[M]. Springer Science & Business Media, 2009. |
| [5] | SORIANO M C, GARCíA-OJALVO J, MIRASSO C R. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers[J]. Reviews of Modern Physics, 2013, 85(1): 421-470. |
| [6] | CALLAN K E, ILLING L, GAO Zheng. Broadband chaos generated by an optoelectronic oscillator[J]. Physical Review Letters, 2010, 104(11): 113901. |
| [7] | ZHUANG J P, CHAN S C. Tunable photonic microwave generation using optically injected semiconductor laser dynamics with optical feedback stabilization[J]. Optics Letters, 2013, 38(3): 344-346. |
| [8] | YAN S L. Period-one characteristic in an optoelectronic delayed feedback semiconductor laser and its application in sensing[J]. Chinese Optics Letters, 2015, 13(4): 040401-040401. |
| [9] | KOUOMOU Y C, COLET P, LARGER L, et al. Chaotic breathers in delayed electro-optical systems[J]. Physical Review Letters, 2005, 95(20): 203903. |
| [10] | CHENGUI GRG,TALLA AF, MB JHT, COILLET A. Theoretical and experimental study of slow-scale Hopf limit-cycles in laser-based wideband optoelectronic oscillators[J]. JOSA B, 2014, 31(10): 2310-2316. |
| [11] | LARGER L. Complexity in electro-optic delay dynamics: modelling, design and applications[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2013, 371(1999): 20120464. |
| [12] | LARGER L, LACOURT P A. From flow to map in an experimental high-dimensional electro-optic nonlinear delay oscillator[J]. Physical Review Letters, 2005, 95(4): 043903. |
| [13] | PEIL M, M JACQUOT, CHEMBO Y K. Routes to chaos and multiple time scale dynamics in broadband bandpass nonlinear delay electro-optic oscillators[J]. Physical Review E, 2009, 79(2): 026208. |
| [14] | WCICKER L, ERNEUX T, D'HUYS O. Slow-fast dynamics of a time-delayed electro-optic oscillator[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2013, 371(1999): 20120459. |
| [15] | LARGER L, SORIANO MC, BRUNNER D. Photonic information processing beyond Turing: an optoelectronic implementation of reservoir computing[J]. Optics Express, 2012, 20(3): 3241-3249. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
