| 过渡金属掺杂GaN的电子结构和光学性质理论研究 |
2. 河北工业大学材料学院, 天津 300130
2. School of Material Science and Engineering, Hebei University of Technology, Tianjin 300130, China
GaN是一种重要的宽带隙半导体材料,具有电子漂移饱和速度高、介电常数小、热导率大、导电性能好、击穿电压高等优点,在高亮度蓝光发光二极管、蓝光激光器和紫外探测器以及抗辐射、高频和高压等电子器件领域有着广阔的应用前景,多年来备受人们的关注[1, 2, 3, 4, 5, 6].为了进一步改善GaN的光电性能,近年来人们对过渡金属掺杂GaN的实验和理论研究产生了浓厚的兴趣[7, 8, 9, 10, 11, 12, 13, 14, 15].Dietl等[7]预言Mn掺杂GaN的居里温度可达400K.Katayama-Yoshida 等[8]采用基于密度泛函理论(DFT)研究了Mn掺杂GaN,发现Ga1-xMnxN(x=0.25)具有稳定的铁磁基态.Nakayama等[9]用muffin-tin 轨道线性组合方法计算了GaN∶Mn的电子结构及掺杂性质.结果表明GaN∶Mn铁磁态的能级比顺磁态和反铁磁态要低,费米能级处电子是自旋极化的,杂质能级位于基本带隙内,而且是强局域化的.Sato等[10]采用Korringa-Kohn-Rostoker方法的相干近似理论研究了Mn掺杂GaN,发现低浓度掺杂时具有稳定的自旋玻璃态,高浓度掺杂时具有稳定的铁磁态.邢海英等[11]研究了Mn掺杂GaN电子结构和光学性质,发现Mn掺杂GaN非常适于自旋注入.实验方面,Sasaki等[12]用MBE法生长了Mn掺杂GaN,研究了Mn掺杂GaN的磁性和输运性质,从实验上得到居里温度超过940 K的Mn掺杂GaN薄膜.Suparna等[13]用光电化学腐蚀法制备了Mg掺杂GaN,发现发光强度增大了3个数量级,低温下发光峰随温度的升高发生蓝移.Polyakov等[14]从实验上研究了Fe掺杂 GaN的光学和电学特性,发现了室温下峰值位于3.37 eV的带边发射和位于2.85 eV的蓝光发射;Feng等[15]用MOCVD法制备了Fe掺杂GaN,研究发现掺杂后GaN电阻率大大提高;Frietas[16]报道了具有半绝缘性质的Fe掺杂GaN;Dashdorj等[17]研究了Fe掺杂 GaN的电荷转移过程.Mei等[18, 19]利用RF-MBE制备了半绝缘Cr∶GaN外延层,发射光谱中出现了与Cr有关的黄色发光带.Jinn-Kong等[20]研究了GaN基太阳能电池的转换效率,发现有Mn掺杂吸收层时转换效率提高了4倍.作为一种半导体光电材料GaN中的缺陷和杂质对材料的电子输运性质和光学性质有很大的影响.虽然人们在理论和实验上对过渡金属掺杂的GaN材料进行了大量的研究,但是理论研究主要集中在磁学性质方面,而对于过渡金属掺杂GaN的光学性质研究较少.
本文从基于密度泛函的第一性原理出发计算过渡族金属(V,Cr,Mn,Fe,Co,Ni)掺杂GaN的能带结构、态密度、介电函数和折射率等性质,分析过渡金属掺杂对GaN的电子结构和光学性质的影响.
1 计算模型和方法理想GaN是六方纤锌矿结构,所属空间群为 P63mc,如图 1(a)所示.GaN的晶格常数实验值是a=b=0.318 9 nm,c=0.518 5 nm,α=β=90°,γ=120°,其中c/a为1.626,比理想六角密堆积结构的1.633稍小,c轴方向Ga—N的键长为0.196 9 nm,其它方向为0.196 5 nm.由于过渡金属离子在GaN体系中至少78%~90%的概率都是占据在Ga位[21, 22, 23],所以研究中掺杂的过渡金属离子仅考虑占据Ga位的情形.采用2×2×1超晶胞体系,每个超晶胞中有8个Ga原子和8个N原子,用一个过渡金属原子取代其中一个Ga原子的位置,掺杂浓度为12.5%.掺杂后的超晶胞结构如图 1(b)所示(以GaN∶Mn为例).
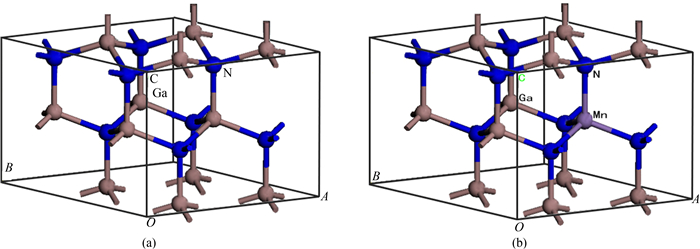 |
| 图1 (a) GaN超晶胞结构和(b) GaN∶Mn超晶胞结构 Fig. 1 (a) Supercells of GaN and (b) GaN∶Mn |
本文采用Materials Studio软件中的CASTEP程序包进行计算.计算中采用平面波赝势法,交换-关联能采用广义梯度近似的PBE近似法[24].截断能选取为450 eV,k网格点设置为4×4×4,单原子能量的收敛标准为1.0×10-5 eV·atom-1,原子间相互作用力收敛标准为0.3 eV·nm-1,晶体内应力收敛标准为0.05 GPa,原子的最大位移收敛标准为0.000 1 nm.晶体中Ga的电子组态为3d104s24p1,N的电子组态为2s22p3,过渡金属的电子组态为3p63dx4s2.计算时先对包含16个原子的超晶胞进行晶体结构优化,再进行内坐标优化,以此为基础来计算未掺杂和掺杂后的GaN的电子结构和光学性质.
2 结果与讨论 2.1 能带结构为了与其它理论研究进行比较,我们首先计算了理想纤锌矿GaN 的能带结构,如图 2所示.可以看出 GaN 是直接带隙半导体,导带底和价带顶都位于布里渊区的G点上,禁带宽度为 1.98 eV,均小于实验值3.39 eV,与邢海英等[25]及Pugh[26]的计算结果一致.能隙的计算结果偏低是由于在计算中采用的密度泛函理论是基态理论[27],而能隙属于激发态,但这并不影响对GaN电子结构的理论分析.
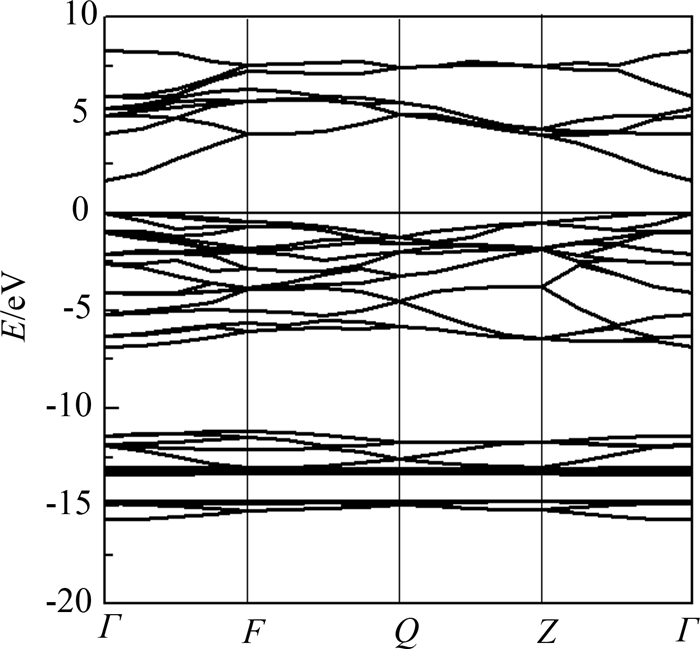 |
| 图2 GaN能带结构 Fig. 2 Energy band structures of GaN |
图 3给出了GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的自旋极化能带结构图.与图 2相比,可以发现掺杂后的GaN仍然为直接带隙半导体,但是由于过渡金属中3d电子的作用,掺杂体系的能量普遍向低能方向移动.另外,掺杂过渡金属后,在一个自旋通道的禁带中出现了杂质能级,这有利于光学跃迁从而改善GaN的光学性能.过渡金属的掺杂也给体系引入了一定量的磁矩.
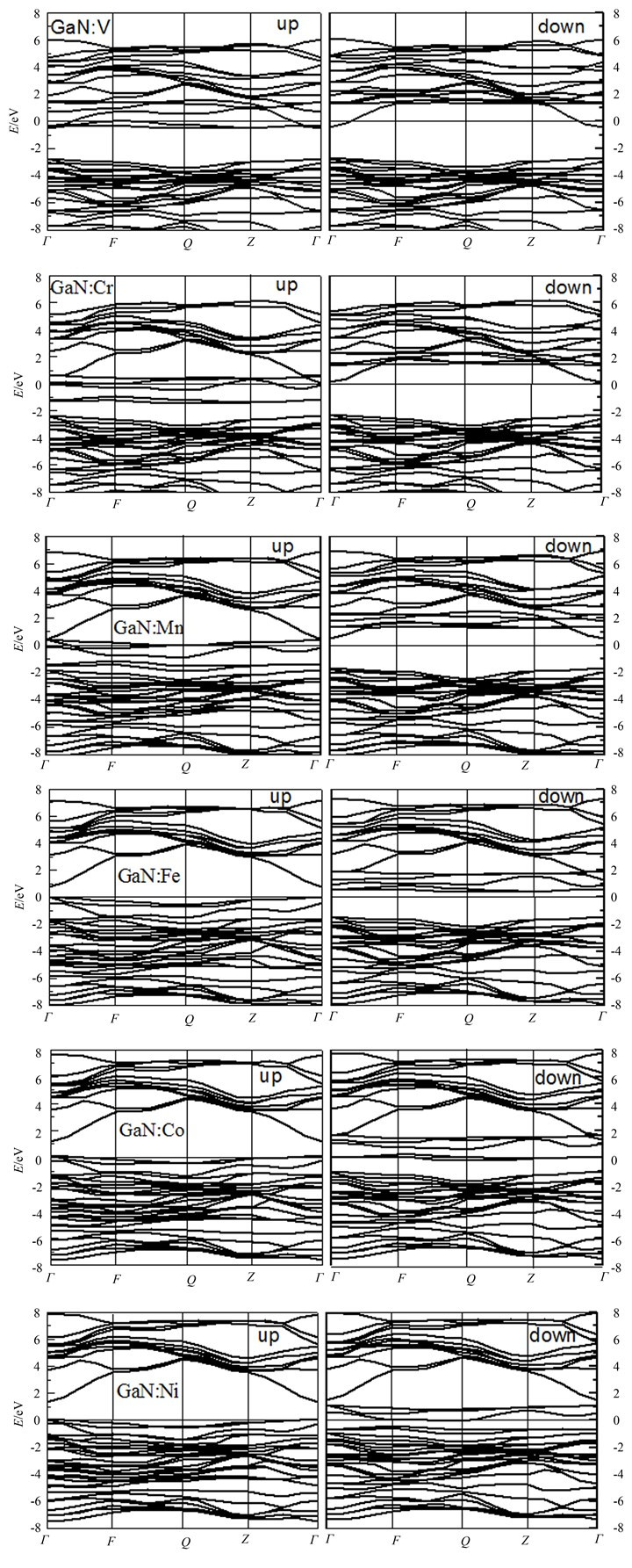 |
| 图3 GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)能带结构 Fig. 3 Energy band structures of GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) |
图 4为GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的总态密度和各个原子的分波态密度图.为了更清楚地了解电子杂化行为,我们也给出了TM掺杂原子的d电子和N原子的s和p电子的态密度图.从态密度图也可以看出,过渡金属的掺杂使GaN的能带向低能方向移动,价带顶不再位于费米能处.对于GaN∶V,在-9.6 eV~-2.7 eV之间的价带主要来自N-2p电子、V-3d电子以及Ga-4s和Ga-4p电子的贡献,能隙中的杂质能带来源于V-3d电子的贡献,而导带部分主要来源于Ga-4s和Ga-4p电子以及少量的N-2p电子和V-3d电子的贡献.对于GaN∶Cr,在-9.3 eV~-2.3 eV之间的价带主要来自N-2p电子、Cr-d电子以及Ga-4s和Ga-4p电子的贡献,能隙中的杂质能带来源于Cr-3d电子的贡献,而导带部分主要来源于Ga-4s和Ga-4p电子以及少量的N-2p电子和Cr-3d电子的贡献.其余的掺杂体系分析类似,就不再一一赘述了.
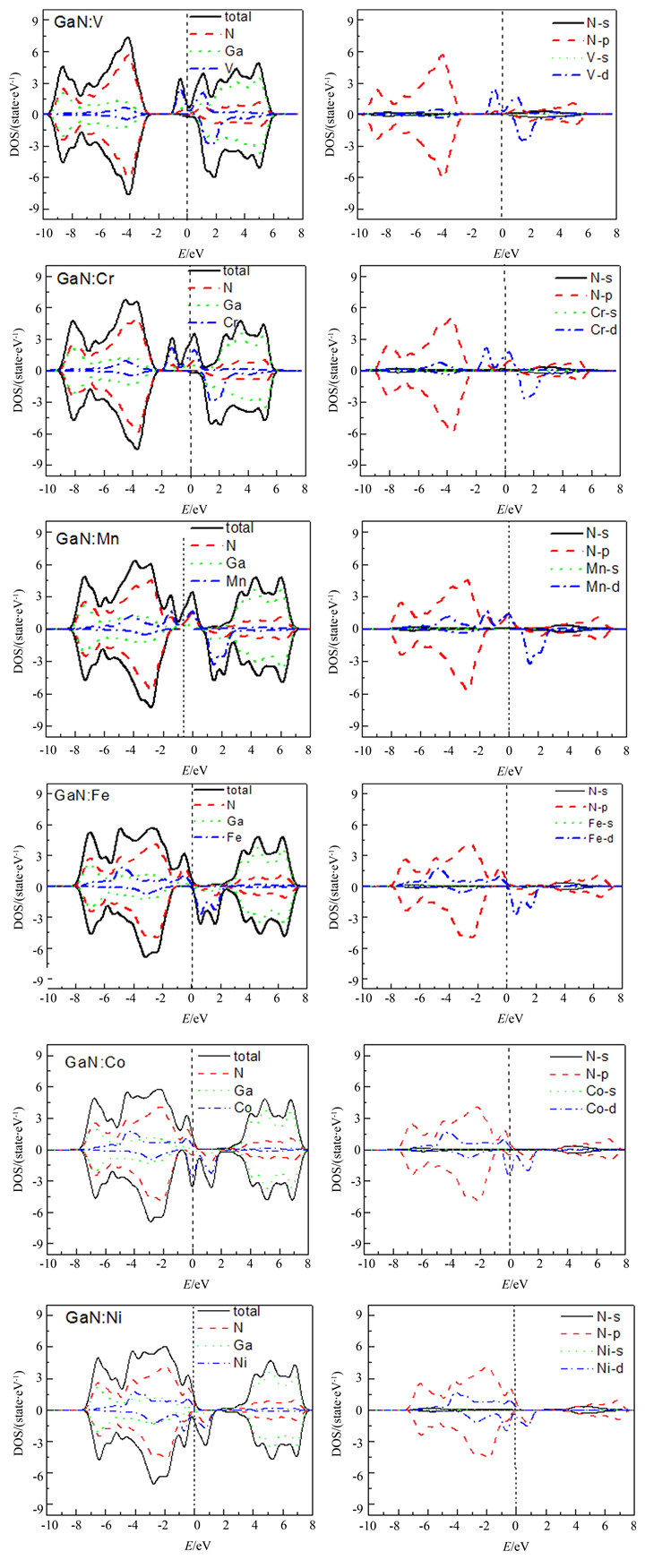 |
| 图4 GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的总态密度和分态密度 Fig. 4 Partial and total densities of state (DOS) for GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) |
另外,由图 4还可以看出,在掺杂体系GaN∶V中,V的3d轨道与N的2p轨道发生了很小的杂化,与过渡金属离子最近的N离子的2p轨道上下自旋劈裂较小;GaN∶Cr 和GaN∶Mn体系中Cr和Mn的3d轨道与N的2p轨道发生了杂化,使得Cr和Mn自旋向上部分3d态往能量较低方向移动,而自旋向下部分3d态被推到费米面以上,3d电子轨道在费米面处产生自旋劈裂,使GaN∶V、GaN∶Cr以及GaN∶Mn体系具有了半金属性;在GaN∶Fe体系中,同样由于Fe的3d电子和N的2p电子的杂化作用使得Fe的3d轨道产生自旋劈裂,在费米面处自旋向上和自旋向下轨道分开,但是在费米面处没有自旋电子,GaN∶Fe仍具有半导体性质;在GaN∶Co和GaN∶Ni体系中Co和Ni的3d轨道电子也产生自旋劈裂,电子首先填充自旋向下的轨道,GaN∶Co和GaN∶Ni体系也具有了半金属性.从态密度图可以看出,不同金属元素掺杂对体系的半金属能隙影响不同,这主要是由于过渡金属离子3d轨道与N的2p轨道杂化程度决定的,pd杂化越强,自旋交换劈裂就越大,决定半金属能隙的自旋带就被推到能量更高的位置.
2.3 光学性质介电函数能够反映固体的能带结构和光学图谱之间的信息,能够表征材料的物理特性. 根据半导体光学性质,在线性响应范围内,其宏观光学性质可以由复介电函数ε(ω)=ε1(ω)+iε2(ω)来描述.根据直接跃迁概率定义和Kramers-Kronig色散关系可以推导出介电函数的虚部和实部分别为[28]
| $ {\varepsilon _2}\left( \omega \right) = \frac{C}{{{\omega ^2}}}\sum\limits_{C,V} {\int_{{\rm{BZ}}} {\frac{2}{{{{\left( {2\pi } \right)}^3}}}} } {\left| {\boldsymbol{e} \cdot {\boldsymbol{M}_{{\rm{CV}}}}\left( \boldsymbol{K} \right)} \right|^2}\delta \left( {E_{\rm{C}}^K - E_{\rm{V}}^K - h\omega } \right){d^3}\boldsymbol{K}, $ | (1) |
| $ {\varepsilon _2}\left( \omega \right) = 1 + \frac{2}{\pi }{\rho _0}\int_0^\infty {\frac{{\omega '{\varepsilon _2}\left( \omega \right)}}{{\omega {'^2} - {\omega ^2}}}{\rm{d}}\omega }. $ | (2) |
其它光学性质与介电函数的关系为:
反射率
| $ R\left( \omega \right) = {\left| {\frac{{{{\left[{{\varepsilon _1}\left( \omega \right) + {\rm{i}}{\varepsilon _2}\left( \omega \right)} \right]}^{1/2}} - 1}}{{{{\left[{{\varepsilon _1}\left( \omega \right) + {\rm{i}}{\varepsilon _2}\left( \omega \right)} \right]}^{1/2}} + 1}}} \right|^2}, $ | (3) |
折射率
| $ n\left( \omega \right) = {\left[{\sqrt {\varepsilon _1^2\left( \omega \right) + \varepsilon _2^2\left( \omega \right)} + {\varepsilon _1}\left( \omega \right)} \right]^{1/2}}/\sqrt 2 , $ | (4) |
消光系数
| $ k\left( \omega \right) = \frac{{{\varepsilon _2}}}{{\sqrt 2 {{\left[{\sqrt {\varepsilon _1^2\left( \omega \right) + \varepsilon _2^2\left( \omega \right)} + {\varepsilon _1}\left( \omega \right)} \right]}^{1/2}}}}. $ | (5) |
如果介电函数虚部起源于光吸收过程,则吸收系数α(ω)可写为
| $ \alpha \left( \omega \right) = \frac{{2\omega l\left( \omega \right)}}{c} = \frac{{\omega {\varepsilon _2}\left( \omega \right)}}{{nc}},$ | (6) |
其中式(1)中下标C,V分别表示导带和价带,BZ表示第一布里渊区,K为倒格矢,|e·MCV(K)|2为动量跃迁矩阵元,C为常数,ω为角频率,ECK和EVK分别表示导带和价带的本征能级.以上公式是分析晶体能带结构和光学性质的主要理论基础,它反映了能级间电子跃迁所产生光谱的发光机理.
由于晶格的对称性,介电函数和折射率为张量,本文中只给出了入射光沿[100]方向的光学物理量.图 5和图 6分别给出了GaN和GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) 的介电函数虚部和反射谱.由图 5可以看出,未掺杂的GaN在0~2.0 eV低能区域介电函数虚部为0,在2.79 eV附近出现介电峰.掺杂后的GaN在低能区均出现介电峰.其中,GaN∶V在低能区1.11 eV处出现介电峰,但是较弱,相应的反射谱图形中在0.99 eV处出现反射肩峰,说明此处有光吸收,主要来自劈裂的自旋向上的杂质带之间的跃迁;GaN∶Cr、GaN∶Mn和GaN∶Co介电函数虚部在低能区出现强介电峰,说明电子跃迁能力很强,对应的能量分别为0.38 eV、0.24 eV和0.13 eV,相应的反射谱图形中在低能区出现反射肩峰,其中GaN∶Cr和GaN∶Mn主要是由劈裂的自旋向上的杂质能级内部跃迁引起的,GaN∶Co主要是由劈裂的自旋向下的杂质能级内部跃迁引起的;GaN∶Fe与未掺杂的GaN相似,在低能区没有介电峰,仅在能隙处有上升边,反射谱中没有出现明显的反射峰,可能在能隙处有较小的光吸收;GaN∶Ni在低能区没有介电峰,但是有逐渐增大的介电函数值,在能隙处可能有较小的光吸收.掺杂后介电峰值所对应的光子能量有略微偏差.在反射谱图形中,反射最强的峰值所对应的光子能量偏差较小.
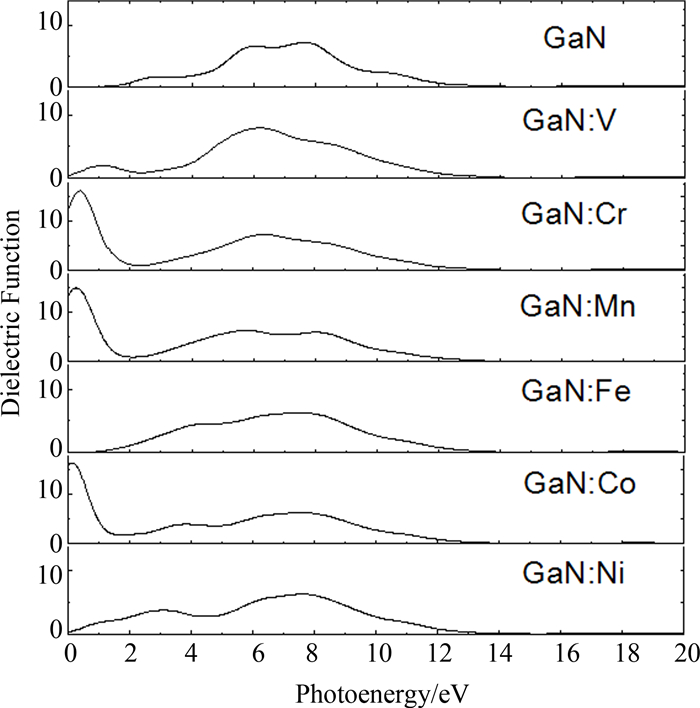 |
| 图5 GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的介电函数虚部 Fig. 5 Imaginary parts of dielectric functions for GaN and GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) |
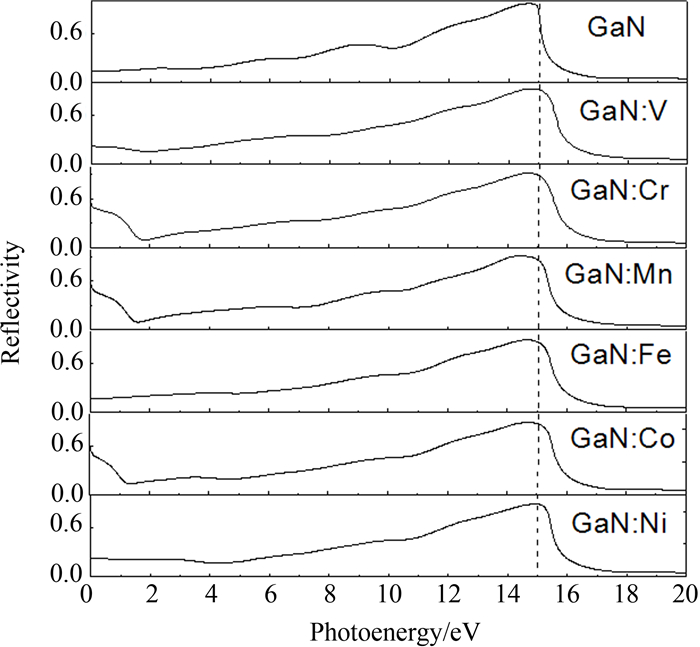 |
| 图6 GaN和GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的反射谱 Fig. 6 Reflectivity for GaN and GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) |
图 7给出了GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) 的复折射率函数.由图 5和图 7可以看出,折射率n和介电函数的虚部变化趋势相同,这和公式(6)理论结果一致.图 7显示未掺杂的GaN 在低能区(小于2 eV)实部为常数,而虚部几乎为0;在高能区(大于15 eV)虚部接近为0,而实部的值变化较小.掺杂后,GaN∶V、GaN∶Cr、GaN∶Mn以及GaN∶Co体系在低能区虚部出现很强的峰值,实部随能量增大而减小,主要是由于掺入过渡金属离子后,在费米面处引入杂质带,电磁波通过的介质不同而引起的变化;GaN∶Fe在低能区与未掺杂的GaN相似,虚部为0,实部接近常数;GaN∶Ni在低能区虚部不为0,也没有出现很强的峰值.由图 7还可以看出,在高能区掺杂体系的复折射率与未掺杂时相似,当光子能量大于15 eV时,折射率几乎为常数,说明掺杂前后材料对高频的电磁波吸收都较弱.
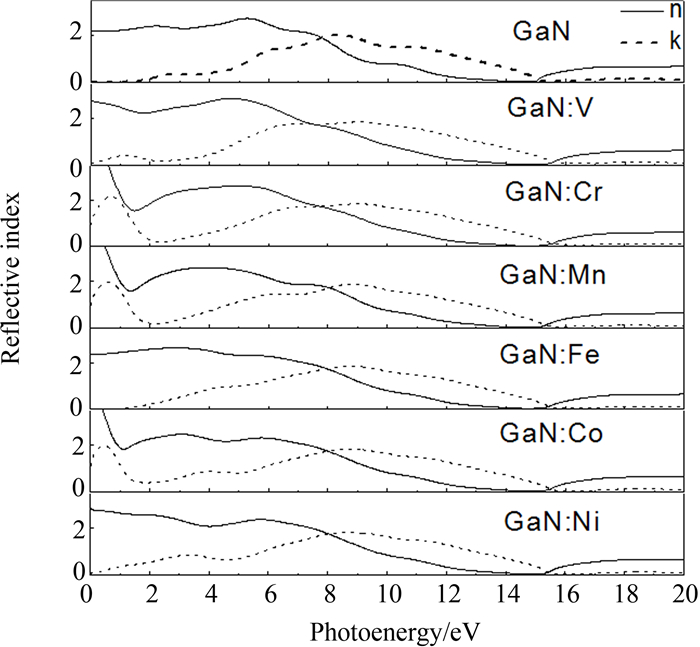 |
| 图7 GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni)的复折射率函数 Fig. 7 Complex refractive index functions for GaN and GaN∶TM(TM=V,Cr,Mn,Fe,Co,Ni) |
采用基于密度泛函理论的第一性原理方法研究不同过渡金属TM(TM=V,Cr,Mn,Fe,Co,Ni)掺杂GaN的能带结构、态密度、介电函数、反射谱及复折射率等性质.计算和分析结果表明,掺杂后没有改变GaN直接带隙半导体的性质,TM(V,Cr,Mn,Fe,Co,Ni) 3d与N的2p由于轨道杂化产生自旋极化杂质带,掺Fe体系仍旧是半导体性质,其它掺杂体系都表现为半金属性.电子结构的变化引起光学性质的变化,掺杂后在费米面处引入了杂质带,除掺Fe和Ni在低能区没有出现光吸收外,其它掺杂体系杂质带内都有电子跃迁,在杂质能级处出现光吸收.本研究为过渡金属掺杂的GaN材料的光电性质实验研究和应用提供理论依据.
| [1] | LI Q Q, HAO Q Y, LI Y, et al. First principle study of Ce doping and related complexes in GaN [J]. Comput Mat Sci, 2013, 72: 32-37. |
| [2] | WANG H G, QIAN Y S, DU Y J, et al. Influence of surface barrier on electron escape probability of gradient-doping GaN photocathode [J]. Chinese J Comput Phys, 2013, 30(5):739-744. |
| [3] | LI Q Q, HAO Q Y, LI Y, et al. Theory study of rare earth (Ce, Pr) doped GaN in electronic structrue and optical property[J]. Acta Phys Sin, 2013, 62(1): 017103-017110. |
| [4] | LI E L, XI M, CUI Z, et al. Electronic structures of unsaturated and H saturated GaN nanowires [J]. Chinese J Comput Phys, 2013, 30(2):277-284. |
| [5] | ZHANG L C, LI Q S, DONG Y F, et al. Electroluminescence from ZnO nanorod/unetched GaN LED wafers under forward and reverse biases [J]. J Opt, 2012, 14: 125601-125606. |
| [6] | MAJID A, DAR A, ZHU J J. Cerium induced ferromagnetic exchange interactions in GaN[J]. J Mag Mag Mat, 2015, 374: 676-679. |
| [7] | DIETL T, OHNO H, MATSUKARA F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors [J]. Phys Rev B, 2001, 63: 195205-195224. |
| [8] | KATAYAMA-YOSHIDA H, KATO R, YAMAMOTO T. New valence control and spin control method in GaN and AlN by codoping and transition atom doping [J]. J Cryst Growth,2001, 231:428-436. |
| [9] | NAKAYAMA H, MARIETTE H,OHTA H, et al. Electronic structure, magnetic ordering, and optical properties of GaN and GaAs doped with Mn [J]. Phys Rev B, 2002, 20(4):045203-045209. |
| [10] | SATO K,KATAYAMA-YOAHIDA H. First principles materials design for semiconductor spintronics [J]. Semicond Sci Technol, 2002, 17:367-376. |
| [11] | XING H Y, FAN G H, ZHAO D G, et al. Electronic structure and optical properties of GaN with Mn-doping[J]. Acta Phys Sin, 2008, 57(10): 6513-6519. |
| [12] | TAKAHIKO S, SAKI S, YOSHIYUKI Y. Magnetic and transport characteristics on high Curie temperature ferromagnet of Mn-doped GaN [J]. J Appl Phys, 2002, 91(10): 7911-7913. |
| [13] | PAL S, INGALE A, DIXIT V K, et al. A comparative study on nanotextured high density Mg-doped and undoped GaN [J]. J Appl Phys, 2007, 101(4): 044311-044317. |
| [14] | POLYAKOV A Y, SMIRNOV N B, GOVORKOV A V. Electrical and optical properties of Fe-doped semi-insulating GaN templates [J]. Appl Phys Lett, 2003, 83(16): 3314-3316. |
| [15] | FENG Z H, LIU B, YUAN F P, et al. Influence of Fe-doping on GaN grown on sapphire substrates by MOCVD [J]. J Crys Grow, 2007, 309(1): 8-11. |
| [16] | FRIETAS J, GOWDA M, TISCHLER J G. Semi-insulating GaN substrates for high-frequency device[J]. J Crys Grow, 2008, 310: 3968-3972. |
| [17] | DASHODORJ J, ZVANUT M E, HARRISON J G, et al. Charge transfer in semi-insulating Fe-doped GaN [J]. J Appl Phys, 2012, 112(1): 013712-013715. |
| [18] | MEI F, WU K M, PAN Y, et al. Structural and optical properties of Cr-doped semi-insulating GaN epilayers [J]. Appl Phys Lett, 2008, 93(11): 113507-11309. |
| [19] | MEI F, YANG Z J, XU J X, et al. Growth and characterization of Cr-doped semi-insulating GaN templates prepared by radio-frequency plasma-assisted molecular beam epitaxy [J]. J Crys Grow, 2012, 353(1): 162-167. |
| [20] | SHEU J K, HUANG F W. Improved conversion efficiency of GaN-based solar cells with Mn-doped absorption layer [J]. Appl Phys Lett, 2013, 103(6): 063906-063908. |
| [21] | TAKEUCHI T, TAGUCHI M, HARADA Y, et al. Electronic structure characteristics of MBE-grown diluted magnetic semiconductor Ga1-xCrxN films [J]. Jpn J Appl Phys, 2005, 44: 153-155. |
| [22] | KEAVNEY D J, CHEUNG S H, KING S T, et al. Role of defect sites and Ga polarization in the magnetism of Mn doped GaN [J]. Phys Rev Lett, 2005, 95: 257201-257203. |
| [23] | WANG J Q, CHEN P P, GUO X G, et al. Magnetic and optical properties of Cr implanted GaN [J]. J Crys Grow, 2005, 275(3-4): 393-397. |
| [24] | PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18): 3865-3868. |
| [25] | XING H Y, FAN G H, ZHANG Y, et al. First principle study of Mg,Si and Mn co-doped GaN [J]. Acta Phys Sin, 2009, 58(1): 450-455. |
| [26] | PUGH S K, DUGDALE D J, BRAND S, et al. Electronic structure calculations on nitride semiconductors [J]. Semicond Sci Technol, 1999, 14(1): 23-31. |
| [27] | PICKETT W E. Pseudopotential methods in condensed matter applications [J]. Comput Phys Rep, 1989, 9(3): 115-119. |
| [28] | SHENG X C. The spectrum and optical property of semiconductor[M]. Beijing: Science Press, 2003,76. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
