| 缺陷TiO2中铁磁性的第一性原理计算 |
2. 浙江省海洋大数据挖掘与应用重点实验室, 浙江 舟山 316022
2. Key Laboratory of Oceanographic Big Data Mining & Application of Zhejiang Province, Zhoushan, Zhejiang 316022, China
2006年,Hong等人[1]在未掺杂TiO2薄膜中发现了室温铁磁性,并且发现在氧气中烧结样品会大大减弱磁性.接下来室温铁磁性于2009年在未掺杂TiO2薄膜[2]和单晶[3],2011年在TiO2体粉末[4]和2013年在TiO2纳米带[5]中被相继发现.在这些实验中类似的现象被发现:在TiO2单晶[3]和体粉末[4]中局域磁矩被归因于Ti3+-VO缺陷复合物,在TiO2薄膜[2]和纳米带[5]中室温铁磁性被归因于VO.同时,Santara等人[5]注意到前驱物TiO2粉末没有显示出任何铁磁性的迹象,尽管其中有大量浓度的VO存在.基于第一性原理计算的一些结果表明在金红石[6]和锐钛矿[6, 7]TiO2中VO都不产生净磁矩,VTi和钛双空位可能是产生铁磁性的原因;但也有结果显示VO可以在金红石[2, 8]和锐钛矿[2, 9]TiO2中引起磁性.这些结果进一步加剧了是VO还是VTi贡献室温铁磁性的争论.同时这也启示我们设定这样一种假设:一种缺陷产生局域磁矩,而另一种缺陷调制长程铁磁有序,室温铁磁性可能是由多缺陷引起的.问题集中在VO和VTi在具有室温铁磁性的未掺杂TiO2中分别起到什么样的作用.第一性原理计算是研究物质电子结构和磁性质的强有力的方法[10, 11].本文采用第一性原理计算方法计算含有VO、VTi,特别是VO和VTi共存的TiO2的电子结构和磁性质,研究未掺杂TiO2中铁磁性的来源.
1 计算细节TiO2存在两个被广泛研究的相:金红石和锐钛矿相.实验[5]发现金红石相TiO2的磁矩比锐钛矿相TiO2的磁矩大,本文计算金红石结构的TiO2.金红石TiO2单胞为的六原子组成的四面体,空间群是P42/mnm,每个Ti原子位于四个基面氧(O1)和两个顶角氧(O2)组成的赝八面体的中心位置.对正分比TiO2和带有单个缺陷的情况,我们采用的2×2×2的超晶胞,对于带有两个缺陷的情况,我们采用了2×2×3的超晶胞.纯密度泛函理论在描述局域态时有着广为人知的局限,这是由于对自相互作用能的不完全抵消而导致了对带隙的低估.额外项U考虑了在相同3d轨道的两个电子之间的排斥作用,可以合理的修正带隙.因此本文对所有的情况都采用了基于全电子全势编码的程序包WIEN2k进行了第一性原理GGA+U的计算.对Ti 3d电子采用的有效相互作用参数是采用限制密度泛函方法计算的Ueff=U-J=5.8 eV [12, 13],Ti和O的最小mufn-tin半径分别为0.9 Å和0.8 Å.Kmax=7.0/Rmt为间隙去的平面波断点,在原子球内部的波函数展开的最大量子数l限定为lmax=10.对2×2×2和2×2×3的超晶胞采用的布里渊区的k网格为2×2×3和2×2×2.在所有的计算中,TiO2的晶格参数被固定为未掺杂TiO2的实验值[14],弛豫内部坐标直至所有原子受力小于0.05 eV·Å-1.
2 计算结果和讨论我们首先计算在金红石TiO2中存在一个VO的情况,VO被很多实验报道认为是引起铁磁性的最重要的缺陷.去掉一个氧后,VO周围的三个Ti原子分别向外移动了0.19Å、0.19 Å和0.21 Å.VO周围的三个Ti原子的3d轨道的电子比正分比情况下的3d轨道的电子分别多了大约0.13,0.13和0.08个电子,这意味着VO点失去了电子带正电荷.而Ti也是正电性的,正是VO和Ti离子之间的相互排斥作用使得VO周围的Ti向外移动.VO在整个超晶胞中引起的总磁矩为2.0 μB,与参考文献[8]的计算结果相同.磁性态比非磁性态更稳定,总能量低96.9 meV.总的态密度图 1(a)显示杂质态刚位于导带底下方,表明VO是浅n型掺杂,这与参考文献[15]的计算结果相符.VO引起的杂质态主要是由Ti-3d组成的,Ti-3d也是磁矩的主要贡献者.这主要是源于VO产生的电子部分占据了其邻近的Ti-3d轨道.图 2(a)显示带有一个VO的TiO2的($ {\rm{\bar 110}} $)面的自旋密度图,如图所示,磁矩主要是由VO周围的三个近邻的Ti原子贡献的.并且VO周围间隙区的电子也被极化了,产生了0.75 μB的磁矩.
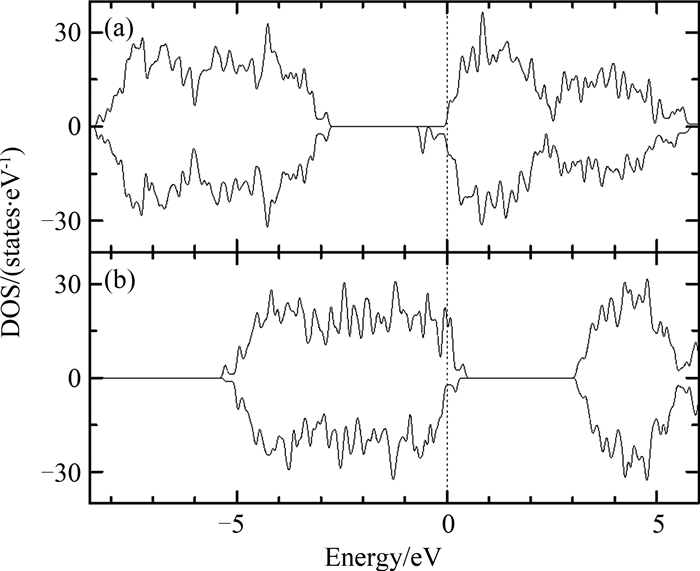 |
| 图1 (a)单个VO的TiO2和(b)单个Ti空位的TiO2的总态密度(费米面用竖直点线标注.) Fig. 1 Total DOSs of TiO2 (a) with one VO and (b) with one VTi (The Fermi level (EF) is denoted by vertical dotted lines.) |
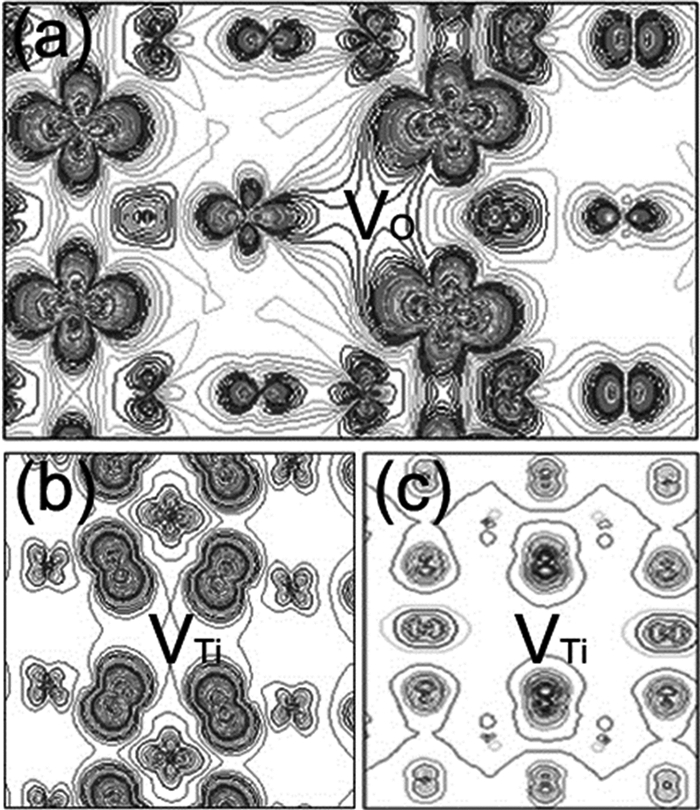 |
| 图2 金红石TiO2(a)($ {\rm{\bar 110}} $)晶面VO附近的自旋密度分布;(b)($ {\rm{\bar 110}} $)晶面VTi附近的自旋密度分布(包括VTi和四个O1);(c)(110)晶面VTi附近的自旋密度分布(包括VTi和两个O2) Fig. 2 Spin density distributions (a) near VO in ($ {\rm{\bar 110}} $) plane; (b) near VTi in ($ {\rm{\bar 110}} $) (consisting of one VTi and four O1) plane; (c) near VTi in (110) (consisting of one VTi and two O2) plane |
接着我们计算了在金红石TiO2中存在一个Ti空位的情况,Ti空位在报道中被认为是有可能在TiO2中产生局域磁矩的缺陷.结构优化之后,VTi周围的O原子向外移动,VTi-O键长从1.95Å和1.98Å变成了2.12Å和2.05Å,这可能是VTi周围的氧的磁矩减小的原因.VTi周围的六个O的2p轨道上的电子比正分比情况下分别少了大约0.1和0.07个电子,说明VTi点带负电并与周围的O离子相互排斥,所以VTi周围的O向外移动.结构优化之后,超晶胞的总磁矩从优化之前的4 μB变成了2.34 μB.图 1(b)为一个VO情况总的态密度图,它显示浅的杂质态出现在价带上方,意味着VTi为浅p型掺杂.图 2(b)和(c)是带有一个VTi的超晶胞的(1-10)面(包括VTi和四个基面O)和($ {\rm{\bar 110}} $)面(包括VTi和两个顶角O)的自旋密度图.它显示VTi周围的间隙区没有被很大地极化,间隙区的总磁矩为0.29 μB.与VO相比,VTi引起的自旋极化更加的巡游,这可能有利于调制长程铁磁交换作用.
为了研究两个VO和两个Ti空位局域磁矩之间的磁耦合作用,我们分别计算在2×2×3超晶胞中能允许的两个VO(VTi)距离最近和最远的情况,如图 3所示,第一个VO(VTi)被固定在a(1)点处,而第二个VO(VTi)分别位于b(2)和c(3)点处.VO-VO距离分别为2.53Å和7.12Å,VTi-VTi距离分别为2.95Å和7.12Å.计算的总能量显示无论是两个VO还是两个VTi的情况,都是远距离的位置更稳定,比近邻的构型能量分别稳定95.3 meV和104.8 meV.对两个VO和VTi稳定的远距离的构型,我们分别进行了铁磁和反铁磁计算.对Ti24O46(Far),与单个VO的情况相比,磁矩还是主要集中在VO点和周围的Ti原子上,但是总磁矩的大小减小了一半,为2 μB.对两个Ti空位的情况Ti22O48 (Far),总磁矩为6 μB,比单个VTi磁矩2.34 μB的二倍要大,这可能是因为VTi之间的较强的铁磁相互作用加剧了VTi周围原子的自旋极化.根据最近邻海森堡模型,反铁磁态和铁磁态的能量差可表示为EAFM-EFM=8J0S2,J0是最近邻磁交换作用,S是缺陷的净自旋.计算结果列于表 1中.从表中可以看出,两个VTi的铁磁态比两个VO的铁磁态更稳定,这跟我们之前的假定是一致的:自旋极化的巡游有利于调制长程铁磁交换作用.
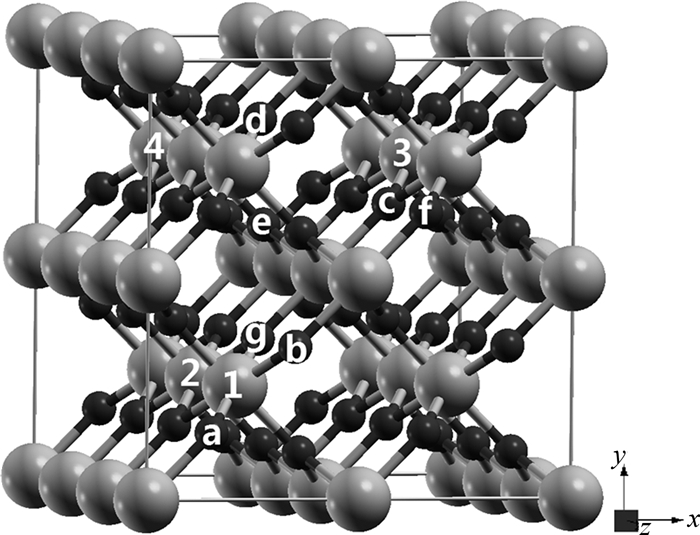 |
| 图3 TiO2单胞的2×2×3超晶胞(Ti:大球,O:小球) Fig. 3 Supercell of 2×2×3 TiO2 unitcells (Ti: big balls, O: small balls) |
| 表1 反铁磁态和铁磁态之间的能量差ΔE=EAFM-EFM, J0(i,j),铁磁 (MMFM) 和反铁磁态(MMAFM)的总磁矩 Table 1 Energy differences between AFM and FM states, and total magnetic moments of FM (MMFM) and AFM (MMAFM) states |
 |
| 点击放大 |
为了研究VO缺陷对两个VTi自旋之间磁耦合的影响,我们计算了在两个Ti空位基础上再加入一个VO的四种情况的铁磁和反铁磁态.两个VTi之间还是处于远距离的位置,1和3的位置,如图 3所示,O原子分别被从d,e,f和g点移走,分别命名为2VTiVO1,2VTiVO2,2VTiVO3 and 2VTiVO4构型.两个VTi加一个VO共引入6个净空穴,使TiO2呈p型,这与我们计算得到的图 4的态密度相符.对于这四种构型,我们计算得到的磁矩都为4.0 μB,这与态密度图 4中显示的1个空穴自旋向上而其它5个空穴自旋向下的结果相一致.对四个构型分别进行了铁磁和反铁磁计算,反铁磁和铁磁态的能量差、J0和磁矩都被列于表 1中.如表 1中所示,2VTiVO2 和 2VTiVO4,两个构型都是铁磁态更加稳定.更为重要的是,与没有VO时两个VTi之间的耦合情况相比,加入VO之后两个VTi之间的铁磁耦合加强了.对于2VTiVO1 和 2VTiVO3,铁磁和反铁磁态几乎是兼并的,在我们的计算精度1.36 meV范围之内.图 5为Ti22O48 (Far) 和2VTiVO4的自旋密度分布,可以看出VO的存在使得自旋密度在空间上更加的连通.这可以总结为:VO引入的电子调制了两个分离的VTi之间的长程铁磁耦合,这跟实验观点是相符的[5].有趣的是,构型2VTiVO2和2VTiVO4出现了亚稳态,净磁矩皆为2.0 μB,比反铁磁态能量上分别更稳定124.6和22.2 meV.
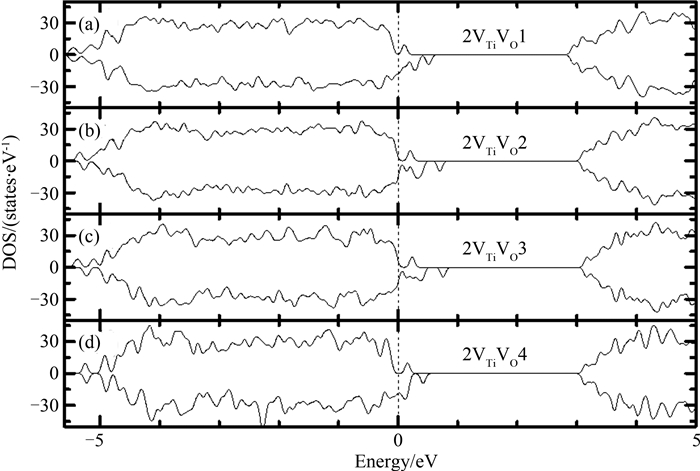 |
| 图4 (a) 2VTiVO1,(b) 2VTiVO2, (c) 2VTiVO3和(d) 2VTiVO4的总态密度(费米面用竖直点线标注.) Fig. 4 Total DOSs of (a) 2VTiVO1, (b) 2VTiVO2, (c) 2VTiVO3 and (d) 2VTiVO4 (The Fermi level (EF) is denoted by vertical dotted lines.) |
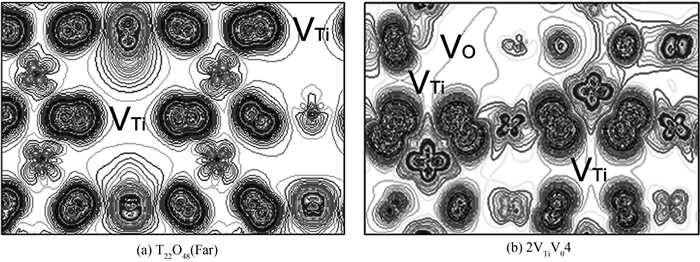 |
| 图5 2×2×3超晶胞($ {\rm{\bar 110}} $)的自旋密度分布 Fig. 5 Spin density distributions in ($ {\rm{\bar 110}} $) plane of 2×2×3 supercell |
同样,通过计算在两个O空位的基础上再加入一个Ti空位的情况,我们研究了Ti空位缺陷对两个VO自旋之间磁耦合的影响.两个VO之间还是处于远距离的位置,a和c的位置,如图 3所示,Ti分别被从1和4点移走,分别命名为2VOVTi1和2VOVTi2构型.计算结果显示这两种构型都没有净磁矩.这是合理的,因为两个VO加一个VTi共引入0个净电荷.为了验证,我们计算了一个VTi加3个VO的情况(有两个净电荷),计算结果显示这种情况产生的磁矩为2.0μB.因此,只要当VO的数量多于VTi的数量二倍时,VO就会对磁矩有贡献,样品的磁矩就会随着VO数量的增多而增加,这跟大部分实验结果相符[1, 2, 3, 4, 5].
3 结论计算了在未掺杂TiO2中单个VO、单个VTi、特别是VTi和VO共存时的电子结构和磁性质.计算表明VTi和VO都可以在TiO2中产生局域磁矩.VTi之间的铁磁耦合比VO之间的铁磁耦合强,更重要地是加入VO之后,VTi之间的铁磁耦合得到了进一步加强.结合得到的态密度和自旋密度分布,结果表明VO引入的电子调制了两个分离的VTi之间的长程铁磁耦合.加入VTi之后,两个VO的的磁矩猝灭,只有当VO的数量多于VTi的数量二倍时,VO才会对磁矩有贡献.此结果验证了VO可以提高铁磁有序,并且当VO的数量多于VTi的数量二倍后,总磁矩随着VO数量的增多而增加,这跟实验结果相符.
| [1] | HONG N H, SAKAI J, POIROT N, et al. Room-temperature ferromagnetism observed in undoped semiconducting and insulating oxide thin films [J]. Phys Rev B, 2006, 73:132404. |
| [2] | KIM D, HONG J, PARK Y R, et al. The origin of oxygen vacancy induced ferromagnetism in undoped TiO2 [J]. J Phys: Condens Matter, 2009, 21:195405. |
| [3] | ZHOU S, CI_ZM_AR E, POTZGER K, et al. Origin of magnetic moments in defective TiO2 single crystals [J]. Phys Rev B, 2009, 79:113201. |
| [4] | SINGHAL R K, KUMAR S, KUMARI P,et al. Evidence of defect-induced ferromagnetism and its “switch” action in pristine bulk TiO2[J]. Appl Phys Lett, 2011, 98:092510. |
| [5] | SANTARA B, GIRI P K, IMAKITA K, et al. Evidence of oxygen vacancy induced room temperature ferromagnetism in solvothermally synthesized undoped TiO2 nanoribbons [J].Nanoscale, 2013, 5: 5476-5488. |
| [6] | YANG K, DAI Y, HUANG B, et al. Density-functional characterization of antiferromagnetism in oxygen-deficient anatase and rutile TiO2 [J]. Phys Rev B, 2010, 81:033202. |
| [7] | PENG H W, LI J B, LI S S, et al. Possible origin of ferromagnetism in undoped anatase TiO 2 [J]. Phys Rev B, 2009, 79:092411. |
| [8] | HAN G B, HU S J, YAN S S, et al. Magnetic properties of rutile TiO2-1/6 from first-principles calculations [J]. Phys Status Solidi-Rapid Res Lett, 2009, 4:236-238. |
| [9] | ZUO X, YOON S D, YANG A, et al. Ab initio calculation on ferromagnetic reduced anatase TiO2-δ [J]. J Appl Phys, 2008, 103: 07B911. |
| [10] | WANG G T, ZHANG L, ZHANG H P, et al. Electronic structure and magnetism of BaTi2Bi2O [J]. Chinese J Comput Phys, 2015, 32: 107-114. |
| [11] | SONG D, NIU Y, XIAO L, et al. First-principles study of structural, electronic, and magnetic properties of Mn-doped ZnS (111) surfaces [J]. Chinese J Comput Phys, 2013, 30:783-790. |
| [12] | ANISIMOV V I, ZAANEN J, ANDERSEN O K. Band theory and Mott insulators: Hubbard U instead of Stoner [J]. Phys Rev B, 1991, 44: 943. |
| [13] | DUDAREV S L, BOTTON G A, SAVRASOV S Y, et al. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study [J]. Phys Rev B, 1998, 57: 1505. |
| [14] | SABINE T M, HOWARD C J. Determination of the oxygen x parameter in rutile by neutron powder methods [J]. Acta Crystallogr B, 1982, 38: 701-702. |
| [15] | CHO E, HAN S, AHN H S, et al. First-principles study of point defects in rutile TiO2-x [J]. Phys Rev B, 2006, 73: 193202. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
