| 合金渗碳体稳定性研究 |
2. 冶金工业过程系统科学湖北省重点实验室, 武汉 430065
2. Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan 430065, China
渗碳体是钢铁材料的重要组成相,合金钢中常常形成合金渗碳体,其稳定性决定钢的组织状态,继而对性能产生影响,如冷加工导致的渗碳体不稳定[1, 2, 3],因此有必要研究合金渗碳体的稳定性.
目前渗碳体的研究已至原子[4, 5]甚至电子水平[6, 7, 8].渗碳体晶体的价电子结构已有许多报道.起初余瑞璜利用固体与分子经验电子理论(EET)[9]计算后指出:渗碳体沿b轴强键络不连续,键络在三维方向的不连续分布导致渗碳体晶体出现脆性[10].随后叶[11]也认为渗碳体在晶轴b方向上可分为强键和弱键层,渗碳体的凝固生长决定于强键层与弱键层间键络的结合力.在徐[12]提出过渡金属复杂化合物的键能计算方法后,黄[13]认为EET计算的最强键键能可以作为相稳定性的判据,但没有考虑不同方向上的键能.刘[14]用EET计算了掺V、Mn、Mo的渗碳体价电子结构,指出:合金元素取代全部4c位置的Fe1原子后,合金渗碳体的强度高于θ-Fe3C.同样刘的计算没有考虑渗碳体不同方向上的键能差异,也没有考虑Fe原子类型对渗碳体性能的影响.而Min[15]在计算了Al2Ca键能不同方向上的差异后发现:键能高且不同方向上的键能差异小,就会使Al2Ca稳定性提高.以上说明,渗碳体的稳定性不仅要考虑价电结构的特点、最强键能,还要考虑键能差异程度.
除EET外,国内外学者也用第一性原理对合金渗碳体的结构特征与稳定性做了许多研究,将合金元素取代Fe的类型细化到Fe1和Fe2.Lv[16]用第一性原理计算Cr和Mn分别取代渗碳体晶胞中4个Fe1和8个Fe2后的稳定性,认为:掺Cr和Mn使渗碳体稳定性增强.Gao[17]则指出,Cr取代4c位置比8d位置更稳定.此外,也有人用第一性原理计算了掺Co和Ni[18, 19],Ti和V[20]渗碳体的稳定性,但都没有计算具体的Fe的数目和位置.
Cr、Mn、Mo、W、V是钢中常用的合金元素,掺入后主要分布在渗碳体中[21, 22, 23]并使之稳定[24].由于渗碳体(θ-Fe3C)晶胞中有4个4c位置的Fe1和8个8d位置的Fe2,所以在合金渗碳体中,要考虑合金元素置换渗碳体晶胞中Fe的类型、数量及位置.上述文献,无论是基于EET还是第一性原理,都没有给出合金元素取代不同位置和数量Fe原子之后的渗碳体(θ-Fe3C)价电子结构及稳定性变化,而这对合金元素及其加入量的选择是重要的.
本文基于EET理论,建立“实际晶胞模型”,参考合金价电子结构参数统计值[25],采用“统计法”计算不同类型(Fe1、Fe2)、数量(1~4个或1~8个)和位置(4c,8d)的Fe被合金元素M(M=Cr、V、Mo、W、Mn)取代后,渗碳体价电子结构的变化.“实际晶胞模型”较“平均晶胞模型”[9, 26, 27]能更好地分析Fe原子被取代时,各原子间关系对价电子结构的影响.通过合金渗碳体晶体结构分析、键能计算,提出稳定性判定因子P;分析了合金渗碳体的稳定性变化规律,从价电子的角度对合金渗碳体的稳定性给予解释.
1 计算方法及依据根据EET理论的BLD[9]方法,用Matlab软件编程计算每种杂阶组合下的每一个不可忽略共价键的理论键距Dnα、共价电子数nα、键距差ΔDα=$\left| \tilde{D}{{n}_{a}}-D{{n}_{\alpha }} \right|$和键能Eα. ΔDα < 0.005 nm时,理论键距与实验键距在一级近似范围,所选原子状态即为实际状态.计算合金渗碳体((M,Fe)3C,M=Cr、V、W、Mo、Mn)价电子结构时,以渗碳体θ-Fe3C晶体结构为计算模型,M原子掺入引起的晶胞参数变化由原子杂化状态变化来体现.
用“统计法”确定BLD多重解,即
| $\bar{n}=\sum\limits_{i}^{{{\sigma }_{N}}}{{{n}_{i}}{{C}_{i}}},{{C}_{i}}=1/{{\sigma }_{N}}$ | (1) |
σN为满足BLD < 0.005 nm的所有原子状态数,ni为共价电子对数.在所有可能原子状态中找出与该组共价电子对数最接近的原子状态组合作为晶胞中原子的实际状态,从而确定原子杂阶,计算出该状态下的键能、晶格电子密度等.
θ-Fe3C为正交晶系,晶格常数a=0.451 44 nm,b=0.507 87 nm,c=0.672 97 nm,属于 Pnma (No.62) 空间群[14],每个晶胞中有4个Fe3C,Fe原子占据两种等效位置,4c位置记为Fe1,8d位置记为Fe2,C原子处在4c等效位置.刘[28]根据第一性原理计算固溶体时采用优化后的Bulk模型为4×4×4的超胞,EET计算考虑中心晶胞及其周围共27个晶胞,即选择3×3×3超胞,对27个晶胞中原子编号.表 1给出了中心晶胞各原子的编号.
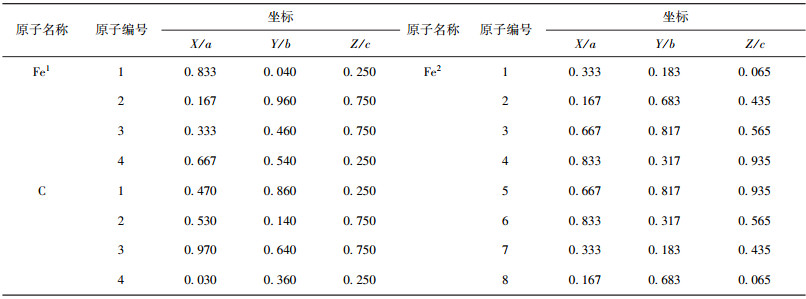
| 表1 θ-Fe3C中心晶胞原子坐标及编号 Table 1 Coordinates and number of atoms in a center unit cell of θ-Fe3C |
 |
| 点击放大 |
根据编号,每个成键原子位置可由数字表示,数字1~8表示中心晶胞内原子,大于8的数字表示处在中心晶胞外原子.例如,原子位置2~3与6~7表示该键两端原子都处在中心晶胞内;1~52表示成键原子一个为中心晶胞内的1号Fe2,一个为周围晶胞中的原子编号为52的Fe2. θ-Fe3C晶胞中按键长排序的前12个键的成键原子位置见表 2.
| 表2 θ-Fe3C晶胞的原子位置 Table 2 Sites of atoms in unit cell of θ-Fe3C |
 |
| 点击放大 |
根据共价电子对数,选取较强的前7个键,画出θ-Fe3C的主要键络结构如图 1所示.图 1显示沿θ-Fe3C的c轴方向,存在明显的分层:C-Fe强键层的共价电子对数n(c-Fe1)=0.967 131,Fe2-Fe2弱键层的共价电子对数n(Fe2-Fe2)=0.202 053.
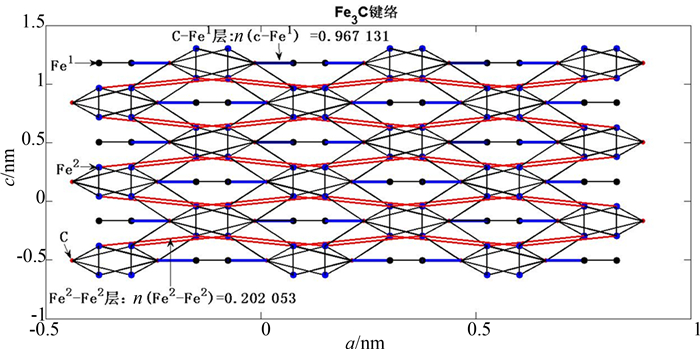 |
| 图1 θ-Fe3C在ac面上的主要键络 Fig. 1 Main bonds of θ-Fe3C on ac plane |
| ${{E}_{\alpha }}=bf{{n}_{a}}/D{{n}_{a}}$ | (2) |
式中, b为元素核电屏蔽作用系数[9, 25]. α为键序,nα为该键上共价电子对数,f为α键上共价电子的成键能力,Dnα表示α键的理论键距.
成键两端原子不同时,键能为
| ${{E}_{\alpha }}={{\bar{B}}_{\alpha }}{{\bar{F}}_{\alpha }}{{n}_{\alpha }}/D{{n}_{\alpha }}$ | (3) |
其中${{\bar{B}}_{\alpha }}$表示共价键两端的异类原子的屏蔽、交换、库伦相互作用系数,${{\bar{F}}_{\alpha }}$表示两原子对α键成键能力的贡献[9].
EET处理固溶体问题大多采用“平均晶胞模型”,认为掺入合金原子后,晶体中的原子是由基体原子和合金原子线性组合而成的混合原子.但“平均晶胞模型”对原子相对位置的影响无法给予清晰描述.实际合金渗碳体晶胞中,M取代Fe原子的相对位置不同,结构性质可能不同.如M取代2个Fe2时,若不考虑原子对称性,由于晶胞中有8个Fe2原子,按照排列组合可能存在的合金渗碳体有28种之多.“平均晶胞模型”认为:M掺入后所有的Fe2都变为Fe2和M组成的混合原子,这28种结构是相同的,即“平均晶胞模型”忽略了取代位置对合金渗碳体的影响.为更接近实际,我们建立“实际晶胞模型”,即考虑取代原子周围环境变化,分别计算M取代不同位置和数目Fe原子的合金θ-Fe3C价电子结构.
2 计算结果计算发现, M取代θ-Fe3C晶胞一个不同位置的Fe1(或Fe2)时,价电子结构差异不明显;但M取代多个不同位置的Fe1(或Fe2)时则差异明显.例如,取代2个Fe2,键长为0.251 465 nm 的Fe2-Fe2,成键两端原子编号见表 2,当2个M原子同时取代中心晶胞内的2、3或者6、7号Fe2原子时,形成的M-M键能显著变大,且键能M-M>Fe2-M>Fe2-Fe2.对于Mn元素,由于元素核电屏蔽作用系数较小,键能:Fe2-Mn>Mn-Mn>Fe2-Fe2.若不成对取代2、3或者6、7号Fe2时,则形成Fe2-M键.因此M取代必须考虑原子的相对位置.
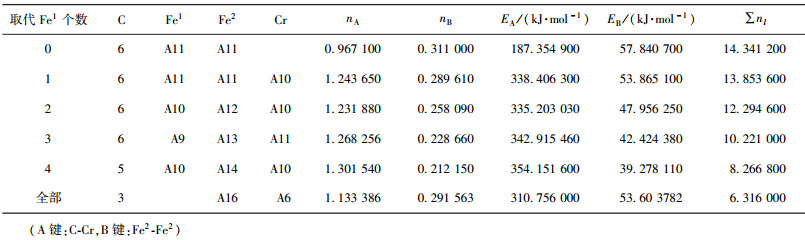
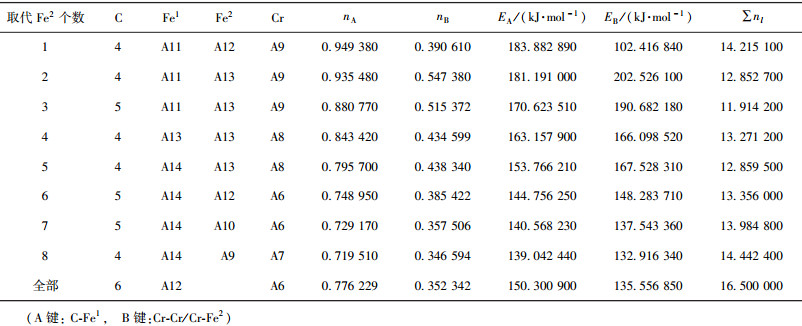
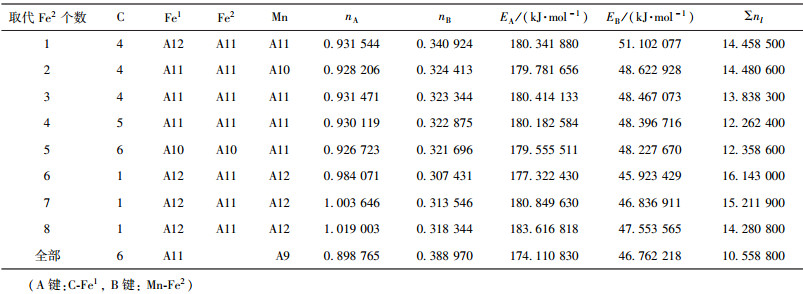
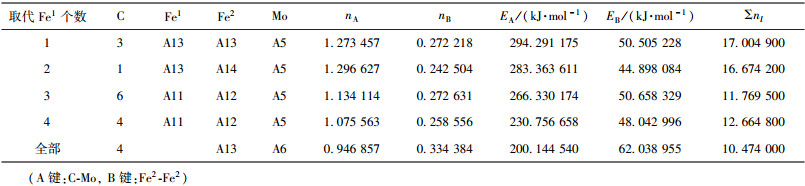
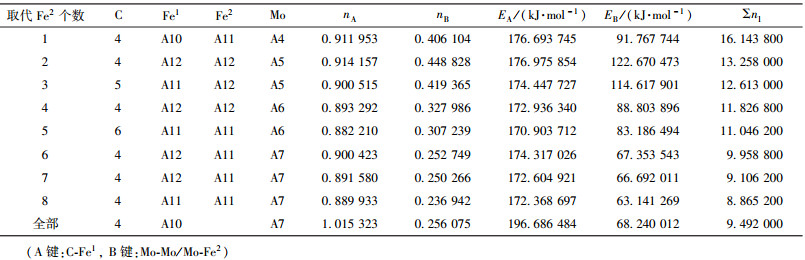
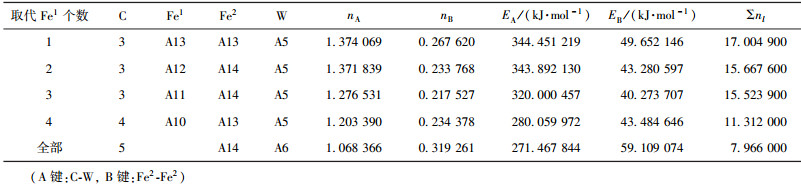
当M成对取代2、3或6、7号Fe2原子时,合金渗碳体的强弱键层差异最小.表 3~表 12给出了M取代不同数量Fe原子时,有强弱键层差异的合金θ-Fe3C价电子结构简表.表中的“全部”表示27个晶胞中的Fe1或Fe2全部被M取代;A代表强健层上最强键,B代表弱键层上最强键.Cr、Mn、Mo、W取代Fe2时,B键在取代个数为1时为Fe2-M,其它为M-M;Mn取代Fe2时,B键为Fe2-Mn.
| 表3 Cr取代Fe1价电子结构 Table 3 VES of cementite with Fe1 substituted by Cr |
 |
| 点击放大 |
| 表4 Cr取代Fe2价电子结构 Table 4 VES of cementite with Fe2 substituted by Cr |
 |
| 点击放大 |
| 表5 Mn取代Fe1价电子结构 Table 5 VES of cementite with Fe1 substituted by Mn |
 |
| 点击放大 |
| 表6 Mn取代Fe2价电子结构 Table 6 VES of cementite with Fe2 substituted by Mn |
 |
| 点击放大 |
| 表7 Mo取代Fe1价电子结构 Table 7 VES of cementite with Fe1 substituted by Mo |
 |
| 点击放大 |
| 表8 Mo取代Fe2价电子结构 Table 8 VES of cementite with Fe2 substituted by Mo |
 |
| 点击放大 |
| 表9 W取代Fe1价电子结构 Table 9 VES of cementite with Fe1 substituted by W |
 |
| 点击放大 |
| 表10 W取代Fe2价电子结构 Table 10 VES of cementite with Fe2 substituted by W |
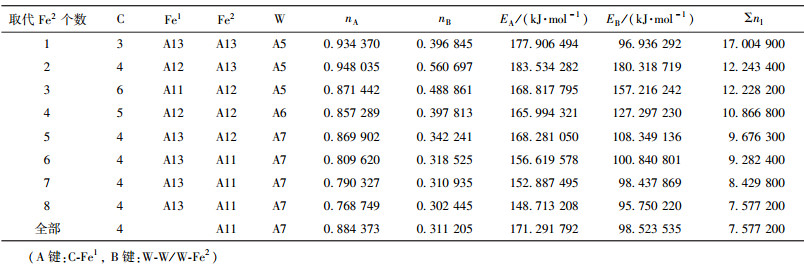 |
| 点击放大 |
| 表11 V取代Fe1价电子结构 Table 11 VES of cementite with Fe1 substituted by V |
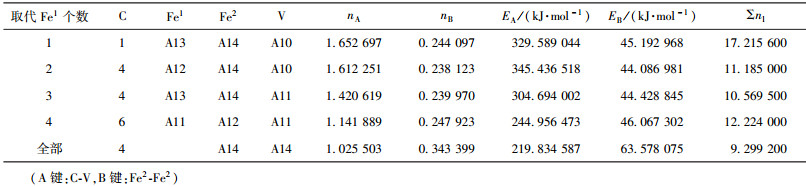 |
| 点击放大 |
| 表12 V取代Fe2价电子结构 Table 12 VES of cementite with Fe2 substituted by V |
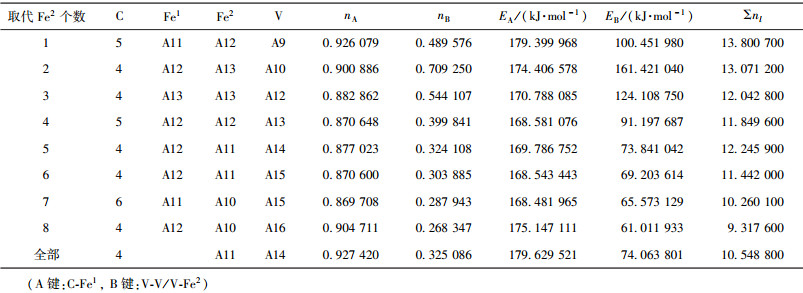 |
| 点击放大 |
根据EET,晶格电子能自由地在晶格间隙移动.晶体受到外力作用时,晶格电子将运动到原键络薄弱处或受到外力作用的削弱处,起到使原子暂时结合的作用,以弥补或调节那里的价电子结构的均匀性,利于晶体继续均匀变形,因此晶格电子代表着金属间化合物的金属性,与塑性有关[9, 29, 30].好的塑性使晶体在外界环境改变时容易保持自身结构,即有利于晶体稳定.晶格电子密度ρVl=∑nl/V[9, 25],其中∑nl表示晶胞所有原子的晶格电子之和,V表示晶胞体积.
晶体中原子键合强度的对称性对稳定性的影响用原子键对称性S来反映[29]:S=Emin/Emax,式中Emin、Emax分别为晶体中最弱与最强键能.晶体键络对称性好,晶体受外力作用变形时更均匀;对称性差,则可能在薄弱地带产生缺陷,导致晶体失稳.由于θ-Fe3C沿c轴方向存在明显的分层,本文计算θ-Fe3C的S因子由EA、EB求得.
成键能力越强,晶体结构越不容易破坏,稳定性越高.晶体单位体积成键能力为[9, 25, 31],FV=∑nαIαFα/V,式中V为晶胞体积,Fα为α键上电子的成键能力,Iα为α键的等同键数,nα为α键上共价电子对数.由于键能表达式中包含共价电子对数nα和成键能力Fα,根据渗碳体明显的强弱层特性,采用强、弱层上最强键键能的几何平均值[32]Q=$Q{{=}^{\left( m+n \right)}}\sqrt{E_{A}^{m}E_{B}^{n}}$来描述合金元素取代Fe1和Fe2后,键络强度的稳定程度.式中,m、n分别为晶胞中A、B键 ( 强、弱键层上的最强键 ) 的数目,EA、EB分别为强、弱键层最强键的键能,单位kJ.mol-1.
综合以上晶格电子密度、原子键合强度对称性和键能的影响,定义稳定性因子P=ρVlSQ.
θ-Fe3C的晶格电子数 ∑nl=14.341 2,Q=73.167 8 kJ·mol-1,弱强键能比S=EB/EA=0.308 7(对于Cr,当取代个数为2~6时, EB>EA,此时S=EA/EB,其它S=EB/EA).合金渗碳体稳定性因子P计算结果见图 2~图 3.
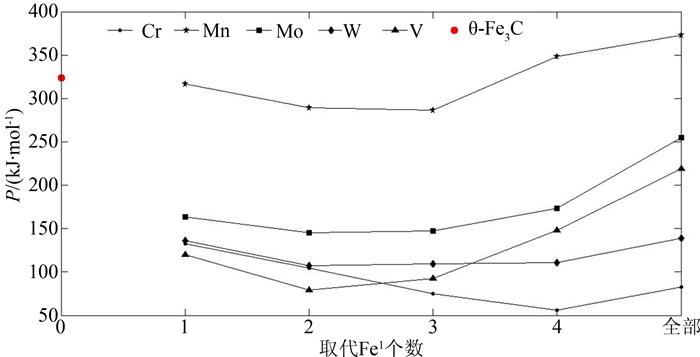 |
| 图2 取代Fe1后的合金渗碳体的P因子 Fig. 2 Factor P of alloyed cementite with Fe1 sustituted by M |
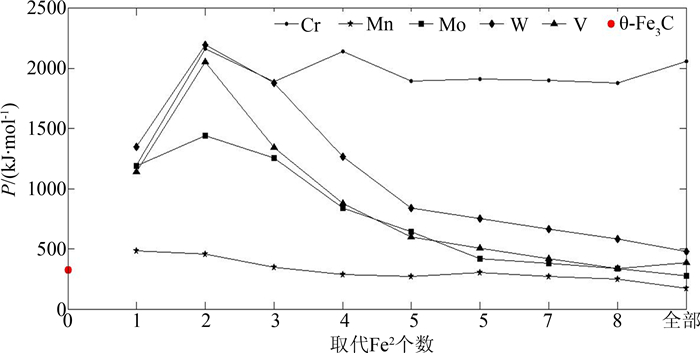 |
| 图3 取代Fe2后的合金渗碳体的P因子 Fig. 3 Factor P of alloyed cementite with Fe2 substituted by M |
比较图 2和图 3发现, M取代Fe2后的P因子比取代Fe1后的大一个数量级,且大于渗碳体θ-Fe3C的P因子.这表明M掺入渗碳体会取代Fe2,该结果与第一性原理计算的相同[16, 20, 33],且Cr、Mo、W、V成对取代2个Fe2时(2、3或6、7位置)最稳定,合金渗碳体的稳定性按W、Cr、V、Mo、Mn的顺序递减.
V、Mo、W取代Fe1后,晶格电子密度先增加后减少;Cr取代Fe1后,晶格电子密度减小;V、Mo、W、Cr合金渗碳体S因子在取代1个Fe1时减小近50%,随后又有不同程度的增加,但是和渗碳体相比S因子较小,这表明V、Mo、W、Cr取代Fe1后,导致强弱键层的差异巨大, Q因子与渗碳体相比也较小,P因子减小,即合金渗碳体稳定性降低.Mn取代Fe1后,晶格电子密度减小;S、 Q因子与渗碳体相当,且随着取代个数增加而略有增加,取代前后稳定性变化先减小后增加,但是变化不明显.
Cr、V、Mo、W取代Fe2后, S因子增大明显,即强弱键层差异减小, S、 Q在取代个数为2处取得极大值.晶格电子密度虽有所下降,但晶体良好的均匀性与键络强度使P增加,合金渗碳体稳定性提高.Mn取代Fe2后, P因子随取代数量的增加略有下降.可见,取代个数为2个Fe2时,合金渗碳体的稳定性按W、Cr、V、Mo、Mn顺序降低.由于晶格电子数与塑性有关,晶体均匀性也会影响晶体的塑性变形,从该角度分析Cr、V、W、Mo取代Fe2时,合金渗碳体键结构均匀、塑性更好,在取代2个Fe2时有极好的塑性,V、W、Cr、Mo、Mn取代Fe2后的渗碳体塑性依次降低.Umemoto[34-35]实验测得的掺Cr和掺Mn合金渗碳体的真应力应变曲线显示,室温下(Fe0.8Cr0.2)3C、(Fe0.8Mn0.2)3C合金渗碳体的塑性都优于θ-Fe3C渗碳体,本文计算结果与之相符.所以, M掺入渗碳体后最可能的化学分子式可表示为θ-(Fe2.5M0.5)C.根据掺Cr和Mn渗碳体的稳定性变化曲线,渗碳体中Cr、Mn元素可以有较大的掺入量.
稳定性因子P的变化可以从电子角度给予解释.M取代一个Fe2时,弱键层上形成Fe2-M键,该键共价电子对数较Fe2-Fe2键大,所以Fe2-M的键能大于Fe2-Fe2键,弱键层因此得到强化.随M取代Fe2数量的增加,逐渐形成Fe2-M、M-M键.对于Cr、V、W、Mo,键能M-M>Fe2-M;对于Mn, M-M < Fe2-M.从表 13可以看出,在强化渗碳体弱键层的过程中,随着M个数的增加,Fe2-M、M-M的等同键数变化趋势不同,Fe2-M键的等同键数增加得更快.当取代(2、3)或者(6、7)号两个Fe2原子时,晶体弱键层形成M-M,且M-M与M-Fe2键数比取得极大,此时M-M键上有最大共价电子对数,S因子与Q因子取得最大;对于Cr、V、Mo、W,P因子取得极大值.继续增加取代个数,Fe2-M键迅速增加,导致分布在M-M键上的共价电子对数减少,M-M键能降低,杂阶随之变化,晶格电子数减小,S与Q因子减小,晶体稳定性降低.
| 表13 M取代Fe2后,M-M和Fe2-M等同键数的变化 Table 13 Variation in equivalent bond number of M-M and Fe2-M with Fe2 substituted by M |
 |
| 点击放大 |
掺Cr和Mn取代Fe2后的P因子变化(图 3)与Mo、W、V不同. Cr在取代较多Fe2时,仍然具有较高稳定性,这是因为Cr对弱键层的强化作用大.弱键层键能在掺Cr后,强度超过原强键层(EB>EA).随取代Fe2个数增加,Fe2-Cr数目增多,Cr-Cr键上共价电子数减少,虽Q因子降低但S因子增大, P因子仍较大,故能保持较高稳定性.Mn由于核电屏蔽作用系数b较小,取代Fe2时,弱键层上最强键为Fe2-Mn,随取代个数增加,Fe2-Mn上共价电子对数减小,键能降低,使其对原弱键层强化作用减弱, S因子略有减小,P因子降低,稳定性下降.在取代个数为6、7、8时,由于晶格电子数增加而使稳定性有所上升.
4 结论EET计算发现:合金渗碳体θ-(Fe,M)3C (M=Cr、V、Mo、W、Mn)的M取代Fe2比取代Fe1更稳定,且Cr、Mo、W、V成对取代在2、3或6、7位置的2个Fe2最稳定.合金渗碳体的稳定性按W、Cr、V、Mo、Mn的顺序递减.Cr、V、W、Mo取代Fe2后,键结构变均匀,通过增强弱键层而提高合金渗碳体稳定性;Mn取代Fe2后,增强效果不明显.合金元素M掺入渗碳体(θ-Fe3C)后,最可能的化学分子式为θ-(Fe2.5M0.5)C.Cr、Mn掺入渗碳体,可有较大的掺入量.
| [1] | WONG J N, CHUL M B, SEI J O, et al. Effect of interlamellar spacing on cementite dissolution during wire drawing of pearlitic steel wires[J]. Scripta Mater, 2000, 42(5):457-463. |
| [2] | HPNO K, OHNUMA M, MUEAYAMA M, et al. Cementite decomposition in heavily drawn pearlite steel wire[J]. Scripta Mater, 2001, 44(6):977-983. |
| [3] | CHAE J Y, JANG J H, ZHANG G H, et al. Dilatometric analysis of cementite dissolution in hypereutectoid steels containing Cr[J]. Scripta Mater, 2011, 65(3):245-248. |
| [4] | LANGUILLAUME J, KAPELSKI G, BAUDELET B. Cementite dissolution in heavily cold drawn pearlitic steel wires[J]. Acta Mater, 1997,45(3):1201-1212. |
| [5] | DANOIX F, JULIEN D, SAUVAGE X, et al. Direct evidence of cementite dissolution in drawn pearlitic steels observed by tomographic atom probe[J]. Mat Sci Eng A, 1998, 250(1):8-13. |
| [6] | ZHOU C T, XIAO B, FENG J, et al. First principles study on the elastic properties and electronic structures of (Fe,Cr)3C[J]. Comput Mater Sci, 2009, 45(4)::986-992. |
| [7] | LI Z L, LIU Z L, LIU W D. Valence electron structure of cementite phase and its interface and the tempering phenomenon[J]. Sci China Ser E, 2002,45(3):282-289. |
| [8] | WUN C C J, EMILY A C. Structure and stability of Fe3C-cementite surfaces from first principles[J]. Surf Sci, 2003, 530(1):88-100. |
| [9] | 张瑞林. 固体与分子经验电子理论[M]. 长春:吉林科学技术出版社, 1993. |
| [10] | YU R H, ZHANG R L, ZHENG W T, et al. Valence structure and properity of cementite[J]. Chinese Sci Bull, 1993, 38(7):665-667. |
| [11] | YE Y F, FAN T X, SHANG Y X, et al. The different coefficient of bonding force between intrastratal and interlamination of M3C type cementite[J]. Sci China Ser E, 1997, 27(4):300-303. |
| [12] | XU W D, ZHANG R L, YU R H. The bonding energy caculation of transition metal compound[J]. Sci China Ser A, 1988, 3, 323-330. |
| [13] | HUANG L, GAO K Y, WEN S P, et al. Valance electron structure analysis of equilibrium and metastable phases of Al3M (M=Ti, Zr, Hf)[J]. Acta Metall Sin, 2012, 48(4):492-501. |
| [14] | LIU Z L, LI Z L, LIU W D. Calculation of the valence electron structures of alloying cementite and its biphase interface[J]. Sci China Ser E, 2001, 44(5):542-552. |
| [15] | MIN X G, SUN Y S, XUE F, et al. Analysis of valence electron structures (VES) of intermetallic compounds containing calcium in Mg-Al-based alloys[J]. Mater Chem Phys, 2003, 78(1):88-93. |
| [16] | LV Z Q, FU W T, SUN S H, et al. First-principles study on the electronic structure, magnetic properties and phase stability of alloyed cementite with Cr or Mn[J]. J Magn Magn Mater, 2011, 33:915-919. |
| [17] | GAO Y, LV Z Q, SUN S H, et al. First principles study on surface structure and stability of alloyed cementite doped with Cr[J]. Mater Lett, 2013, 100:170-172. |
| [18] | WANG C X, LV Z Q, FU W T, et al. Electronic properties, magnetic properties and phase stability of alloyed cementite (Fe,M)3C (M-Co,Ni) from density-functional theory calculations[J]. Solid State Sci, 2011, 13:1658-1663. |
| [19] | GAO Y, WANG B, GUO M W, et al. First-principles study on surface structural, magnetic and electronic properties of alloyed cementite with Co or Ni[J]. Comp Mater Sci, 2014, 85:154-158. |
| [20] | WANG B W, XIE Y P, ZHAO S J,et al. Density functional theory study of the influence of Ti and V partitioning to cementite in ferritic steels[J]. Phys Status Solidi B, 2014, 251:950-957. |
| [21] | UMEMOTO M, LIU Z G, MASUYAMA K, et al. Influence of alloy additions on production and properties of bulk cementite[J]. Scripta Mater, 2001, 45(3):391-397. |
| [22] | LIU Q D, CHU Y L, WANG Z M, et al. 3D Atom probe characterization of alloying elements partitioning cementite of Nb-V Microalloying steel[J]. Acta Metall Sin, 2008, 44(11):1281-1285. |
| [23] | DUNLOP G L, CARLSSON C J, FRIMODIG G. Precipitation of VC in ferrite and pearlite during direct transformation of a medium carbon microalloyed steel[J]. Metall Trans A, 1978, 9(2):261-266. |
| [24] | SHEIN I R, MEDVEDVA N I, IVANOVSKII A L. Electronic structure and magnetic properties of Fe3C with 3d and 4d impurities[J]. Phys Status Solidi B, 2007, 244(6):1971-1981. |
| [25] | 刘志林, 林成. 合金电子结构参数统计值及合金力学性能计算[M]. 北京:冶金工业出版社, 2008. |
| [26] | LI J P, MENG S H, HAN J C, et al. Valence electron structure and properties of the ZrC1-xNx solid solution[J]. Rare Metal Mat Eng, 2008, 37(6):980-983. |
| [27] | PENG K E, YI M Z, RAN L P. Valence electron structure and properties of (Mo1-x,Wx)Si2 solid solutions[J]. Rare Metal Mat Eng, 2010, 39(3):414-416. |
| [28] | LIU X J, REN Y. Solid solution structure and elastic modulus of single atom in transition metal nitrides:First principle studies[J]. Chinese J Comput Phys, 2013,30(3):433-440. |
| [29] | JIANG S Y, LI S C. Valence electron structures and properties of Al-Ce compounds[J]. Rare Metal Mat Eng, 2013,42:397-400. |
| [30] | JIANG S Y, LI S C. Effect of valance electron structure of La-Al compounds on aluminum alloy properties[J]. Trans Mater Heat Treat, 2013, 34(7):31-35. |
| [31] | SU J H, JIANG T, REN F Z. Effect of Cr on electron structure and properties of copper[J]. Trans Mater Heat Treat, 2012, 33(4):152-155. |
| [32] | LUO X G, LI J P, HU P,et al. Empirical electron theory model for calculating hardness of covalent crystals[J]. Chinese Sci Bull, 2010, 55(19):1957-1962. |
| [33] | CHAITANYA K A, MARCEL H F S. First-principles prediction of partitioning of alloying elements between cementite and ferrite[J]. Acta Mater, 2010, 58(19):6276-6281. |
| [34] | UMEMOTO M, LIU Z G, MASUYAMA K,et al. Influence of alloy additions on production and properties of bulk cementite[J]. Scripta Mater, 2001, 45(4):391-397. |
| [35] | UMEMOTO M, TODAKA Y, TAKAHASHI T, et al. Characterization of bulk cementite produced by mechanical alloying and spark plasma sintering[J]. J Metastable Nanocrystal Mater, 2003, 15:607-614. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

