| 飞秒激光参数对四态阶跃型分子光电子能谱的影响 |
Autler-Townes (AT)分裂是强激光与物质相互作用的非线性现象[1].研究发现激光场强[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25],波长[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25],脉宽[6, 7, 21, 22, 24],脉冲形状[25]和延时[2, 3, 12]影响AT分裂. 理论和实验上有对不同构型的多态原子/分子体系的研究.
通过泵浦-探测技术可观测到三态体系的AT双分裂. Wollenhaupt等人[2, 3]实验上观察到阶跃型K原子光电子谱的AT双分裂,研究了泵浦场强和延时对AT分裂的影响.他们认为不对称分裂由非共振激发引起,分裂间距随场强的增强而增大. Peng和Zheng[4]认为泵浦场强和失谐影响V型体系AT双峰分裂间距,位置和峰高. Zhang等人[5]认为介质粒子数密度影响飞秒激光脉冲在Λ型三能级原子介质的传播和光谱特性. Sun和Lou[6]理论研究了泵浦场强和脉宽对阶跃型Na2的AT双分裂的影响.长脉宽可能导致不对称双峰. Yuan等人[7]研究了分子转动和取向对阶跃型Na2的AT双分裂的影响. Yao等人[8, 9]研究了阶跃型K2的AT双分裂,认为泵浦场强和波长决定分裂间距和峰高.
四态体系的AT分裂与三态体系有一些相似的特点. Wei等人[10]和Han等人[11]认为V-型原子吸收谱的双/三分裂依赖于第二个驱动场的场强和波长. Liu和Fan[12]认为两驱动场之间相对位相影响准Λ型四能级系统中的传播效应. 一些研究认为驱动场失谐影响Λ-型原子体系电磁诱导透明(EIT)共振中双/三分裂谱峰位置和峰高[13, 14, 15, 16]. Echaniz等人[17],Dutta等人[18] 和Wang 等人[19]认为驱动场场强和失谐影响N-型原子双/三分裂间距及谱峰峰高. Sandhya[20]研究认为中间跃迁耦合较强时,三驱动场中阶跃型原子体系的吸收谱为三峰(动力学分裂).
对于四态阶跃型体系,Meier等人[21, 22]和Hu等人[23, 24]观察到三驱动场中Na2/Li2的AT三分裂,研究了脉宽对AT分裂的影响. 长脉宽可能导致不对称AT三分裂. Yao和Zheng[25]在近共振区观察到K2的不对称AT三分裂,研究了同时改变三驱动场的参数时,激光场强,波长和形状对AT分裂的影响. 他们没有研究共振和远共振区的情况. 他们也没有研究单一激光场参数对AT分裂的影响.
以上关于AT分裂对激光场强和波长依赖性研究的对象多是四态 N,V,和Λ 构型[9, 10, 11, 12, 13, 14, 15, 16, 17]. 很少关于阶跃型构型的研究[19, 20, 21, 22, 23]. 第二束泵浦激光场强和波长对四态阶跃型K2 分子AT分裂影响的研究未见报道. 本文利用含时波包法,研究了泵浦1-泵浦2-探测激光场中四态阶跃型K2分子光电子谱的AT分裂. 分别讨论了泵浦2激光场共振,近共振区和远共振区三种情况下AT分裂的特点.
1 基本理论采用K2分子的四态模型: 基态|X〉(|X〉1Σg+),激发态|A〉(|A〉1Σu+)和|2〉 (|2〉1Πg+),和电离态|X+〉(|X+〉2Σg+)[25, 26, 27],如图 1所示. 计算中忽略分子的旋转自由度.
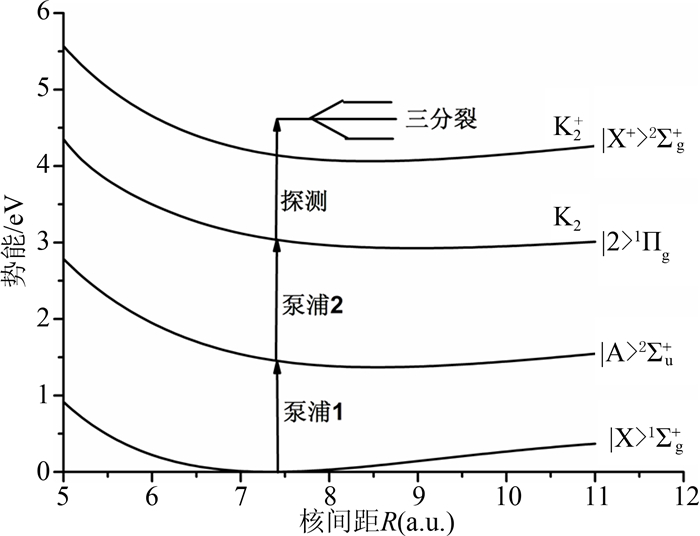 |
| 图1 K2分子势能曲线(箭头分别表示激发能1.462 eV (848 nm), 1.579 eV (785 nm), 和1.579 eV (785 nm).) Fig. 1 Potential energy curves of K2 molecule(The arrows indicate excitation energies of 1.462 eV (848 nm), 1.579 eV (785 nm), and 1.579 eV (785 nm), respectively.) |
采用波恩-奥本海默近似,分子波函数Ψ满足含时薛定谔方程
| ${\text{i}}\hbar \frac{\partial }{{\partial t}}\psi = H\psi ,$ | (1) |
系统的哈密顿量H可以写为
| $H = {H_S} + H' = T + V + H',$ | (2) |
其中,T是核的动能算符,V是系统的势能算符,H′是K2分子与激光场的相互作用项.对此四态模型,波函数可以写成为
| $\psi = {\left( {{\psi _{\text{X}}},{\psi _{\text{A}}},{\psi _2},{\psi _{{\text{ion}}}}} \right)^{\text{T}}},$ | (3) |
| ${\psi _{{\text{ion}}}} = {\left( {{\psi ^{\left( 1 \right)}},{\psi ^{\left( 2 \right)}},\cdots ,{\psi ^{\left( N \right)}}} \right)^{\text{T}}},$ | (4) |
其中,N表示K2分子电离态的数目.
动能算符T可以表示为
| $T = - \frac{{{\hbar ^2}}}{{2\mu }}\frac{{{\partial ^2}}}{{\partial {R^2}}}\left( \begin{gathered} 1\;0\;0\;o \hfill \\ 0\;1\;0\;o \hfill \\ 0\;0\;1\;o \hfill \\ \tilde o\;\tilde o\;\tilde o\;I \hfill \\ \end{gathered} \right),$ | (5) |
其中,μ是K2分子的折合质量,R是核间距.o=(0,0,…,0)是一个N维的零向量,$\tilde o$是o的转置向量,I是一个N×N维的单位矩阵.
势能算符V可以表示为
| $V = \left( \begin{gathered} {V_{\text{X}}}\;0\;\;0\;o \hfill \\ 0\;\;{V_{\text{A}}}\;0\;o \hfill \\ 0\;\;0\;\;{V_2}\;o \hfill \\ \tilde o\;\;\tilde o\;\;\tilde o\;V \hfill \\ \end{gathered} \right),$ | (6) |
其中,VX,VA和V2分别表示基态|X〉,激发态|A〉和|2〉的势能面. V是一个N×N维矩阵,用来描述K2分子离散化的电离态,其表示形式
| $V = {V_{\text{X}}} + I + \left( \begin{gathered} {\xi ^{\left( 1 \right)}}\;\;0\;\;\; \cdots \;0 \hfill \\ 0\;\;\;\;{\xi ^{\left( 2 \right)}} \cdots 0 \hfill \\ \; \vdots \;\;\;\; \vdots \;\;\;\;\;\;\;\; \vdots \hfill \\ 0\;\;\;\;0\;\;\;\; \cdots {\xi ^{\left( N \right)}} \hfill \\ \end{gathered} \right),$ | (7) |
其中,ξ(i)=(i-1)Δξ(i=1,2,…,N)是出射光电子能量.
K2分子与激光场的相互作用项可以表示成
| $H' = \left( \begin{gathered} 0\;\;\;{W_{{\text{XA}}}}\;\;\;0\;\;\;o \hfill \\ {W_{{\text{XA}}}}\;0\;\;\;{W_{{\text{A2}}}}\;\;o \hfill \\ 0\;\;\;{W_{{\text{XA}}}}\;\;\;0\;\;\;{W_{2i}} \hfill \\ \tilde o\;\;\;\;\;\tilde o\;\;\;{{\tilde W}_{2i}}\;\;O \hfill \\ \end{gathered} \right),$ | (8) |
其中,${\tilde W_{2i}} = \left( {W_{2i}^{\left( 1 \right)},W_{2i}^{\left( 2 \right)},\cdots ,W_{2i}^{\left( N \right)}} \right)$是一个N维行向量,向量元表示的是|2〉态和|X+〉态在外场下的耦合,O是一个N×N维零矩阵. 两个电子态在外场下的耦合可以写成
| $\begin{gathered} {W_{{\text{XA}}}} = \hbar {R_1}\left( R \right)\cos \left( {{\omega _1}t} \right),\hfill \\ {W_{{\text{A2}}}} = \hbar {R_2}\left( R \right)\cos \left( {{\omega _2}t} \right),\hfill \\ {W_{{\text{2i}}}} = \hbar {R_3}\left( R \right)\cos \left( {{\omega _3}t} \right),\hfill \\ \end{gathered} $ | (9) |
其中,${R_1} = {\mu _{{\text{XA}}}}\left( R \right){e_1}f\left( t \right)/\hbar ,{R_2} = {\mu _{{\text{A2}}}}\left( R \right){e_2}f\left( t \right)/\hbar $和${R_3} = {\mu _{{\text{2i}}}}\left( R \right){e_3}f\left( t \right)/\hbar $分别是激光场|X〉→A〉态,|A〉→2〉态和|2〉→X+〉态的Rabi频率. μXA(R),μA2(R)和μ2i(R)是电子态的跃迁偶极矩,e1,e2,e3是激光场的幅值,ω1,ω2,ω3是它们的角频率,脉冲包络采用高斯形式f(t)=exp[-4ln2(t/τ)2]. τ是脉宽,本文计算取值 30 fs.
| $P\left( {{\xi ^{\left( i \right)}}} \right) = \mathop {\lim }\limits_{t \to \infty } {\int {{\text{d}}R\left| {{\psi ^{\left( i \right)}}\left( {R,t,{\xi ^{\left( i \right)}}} \right)} \right|} ^2}.$ | (10) |
势能曲线取自文献[28, 29, 30]. 跃迁偶极矩取自文献[31]. 本文出射光电子能ξ((i)的取值范围为0~2 eV,电离态数目N为120. 采用分裂算符-傅里叶变换法数值求解含时薛定谔方程[32, 33].
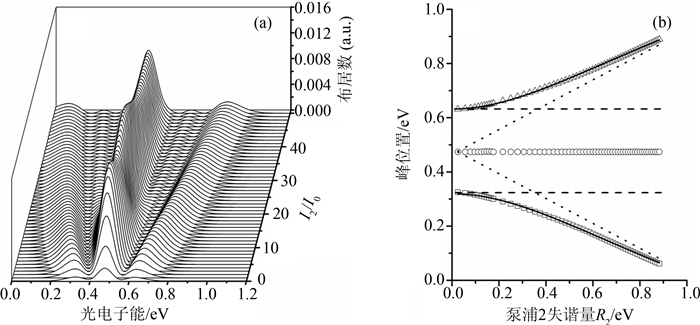
2 结果和讨论图 2(a)是不同泵浦2激光场强的光电子能谱图. 激光参数: I0=1.0×1011 W·cm-2,I1=I3=4I0,λ1=848 nm,λ2=λ3=785 nm,τ=30 fs.光电子谱呈现对称三分裂. Yao和Zheng在泵浦1激光场的近共振区(λ1=λ2=λ3=785 nm)观察到K2分子的不对称三分裂. 但他们对于共振情况未做研究[25]. 此对称三分裂在Na2分子[21, 22]和Li2分子[23, 24]的研究中已有报道.这与较强中间跃迁耦合作用下(R2$ \gg $R1,R3)四态原子体系的三峰吸收谱(动力学分裂)类似[10, 11, 14, 15, 17, 20]. 光电子能谱的这种分裂模式就是AT分裂.它可以用缀饰态理论的ac-Stark 分裂来解释: 双峰结构是由共振电离过程中足够强的Rabi振荡引起的[6, 21, 22, 23, 24, 25]. 缀饰态理论中,激发态|2〉在外加激光场作用下分裂为三个亚稳态,它们分别对应于光电子能谱中三峰. 图 2(a)可见三分裂间距随泵浦2激光场强的增强而增大. 这与对三态K[2, 3],K2[8, 9],Na2[6],和四态 K2分子[25]的研究结果相似. 相似特征也出现在与三激光场相互作用的四态原子的吸收谱中[10, 11, 14, 15, 16, 17, 18, 19, 20, 34].图 2(b) 是谱峰位置随泵浦2激光Rabi频率的变化图. 中间峰位置在 0.474 eV,由${E_{v0}} + \sum \hbar {\omega _k} - {V_I}\left( {{R_0}} \right)$[6, 21, 23]得到,Ev0是振动基态的能量,$\hbar {\omega _k}$是光子能量,VI(R0)是|X+〉态在中性分子基态平衡核间距R0处的势能(如图 1所示). 三峰中心位置如图 2(b)中实线所示分别为 0.474-R/2,0.474,0.474+R/2(有效核间距$R = \sqrt {R_1^2 + R_2^2} $[2, 11, 14, 19, 21, 22, 23, 24, 25, 35],这与数值结果一致. 当泵浦2激光场强较弱时(R2$ \ll $R1),AT分裂正比于R1/2 (如图 2(b)中虚线所示). 当泵浦2激光场强较强时(R2$ \gg $R1),AT分裂正比于R2/2 (如图 2(b)中点线所示).
 |
|
图2
(a) 不同泵浦2激光场强的光电子能谱,(b) 谱峰位置与泵浦2场Rabi频率R2的关系 (曲实线表示缀饰态理论结果. 虚直线和点直线分别表示R2$ \ll $R1和R2$ \gg $R1的渐近行为.) Fig. 2 (a) Photoelectron spectra at various Pump-2 laser intensities I2, (b) Peak positions versus Pump-2 Rabi frequency R2 (Curves in solid lines show result using dressed-state formalism. The dashed straight lines and dotted straight lines indicate asymptotic behaviors for R2$ \ll $R1andR2$ \gg $R1, respectively.) |
图 3(a)是泵浦1激光共振,不同泵浦2激光波长的光电子能谱图. 激光参数: I0=1.0×1011 W·cm-2,I1=I2=I3=4I0,λ2=λ3=785 nm,τ=30 fs. 泵浦2激光场失谐量为Δ2=ω2-ω2A,ω2A是A〉→2〉态的固有频率. 当泵浦2激光共振时,光电子谱为对称三分裂:一个中间峰和两个边峰,非共振时为不对称三分裂. 此不对称性已经在对K原子[2],K2 分子[8, 9]和四态原子[18, 19, 34]的研究中观察到.泵浦2激光波长增加,三峰向低能方向移动. 这是因为波长越长,光子能量越小,从而导致光电子能量越低.这与三态K2分子在正弦型和方波型脉冲包络激光场的研究结果相似.高斯型脉冲情况未有研究[25]. 激光波长(也即脉冲频率)引起频谱移动在较大分子中也观察到[36]. 图 3(b)是谱峰位置随泵浦2场失谐量Δ2的变化图. 三峰的位置分别是0.311+0.986Δ2,0.475+0.278Δ2,和 0.641+0.981Δ2. 这表明三峰位移量不相等: 中间峰位移1/4Δ2,两个边峰位移Δ2.四态阶跃型分子光电子谱谱峰能量位移行为未见报道.Echaniz等人[17]研究了四态N-型Rb吸收谱中三峰位置与耦合场Rabi频率和失谐量的依赖关系. 他们认为谱峰位移量与失谐量不是线性关系.图 3(b)可见,泵浦2激光非共振时,三峰中相邻两峰间距不相等. 此现象与失谐场中对四态原子的研究结果一致[16, 19, 24]. 三峰中两边峰间距(0.370 eV)不变. 在近共振区(695 nm≤λ2≤895 nm),当泵浦2激光场偏离共振,三峰逐渐变为双峰. 类似现象在四态V-型原子的研究中有报道[10].当泵浦2激光场失谐量为±R1/2 (λ2=695 nm 或 895 nm)时,一个边峰与位移的中间峰交叉,如图 3(b)所示. 文献7中用双缀饰态解释此现象.此交叉也在文献[17]中提到. 图 3也显示了泵浦2激光场远共振区(Δ2>R1/2,即λ2 < 695 nm 和 λ2>895 nm),波长对AT分裂的影响. 当泵浦2激光场失谐量Δ2较大时,光电子谱为AT双峰. 双峰分裂间距(0.370 eV)不因泵浦2激光波长改变而改变.
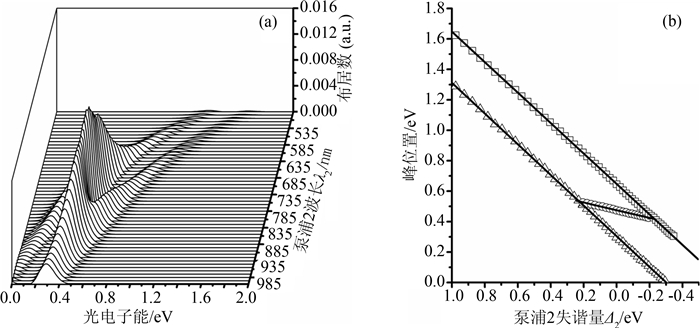 |
| 图3 (a) 泵浦2激光共振,不同泵浦1激光波长(648 nm~1 188 nm)的光电子能谱, (b) 谱峰位置与泵浦1场失谐量Δ1的关系. Fig. 3 (a) Photoelectron spectra at various Pump-2 laser wavelengths (485 nm~1 005 nm) with Pump-1 resonant, (b) Peak position versus Pump-2 detuning Δ2 |
当泵浦2激光场失谐量为R1/2(λ2=695 nm)时,光电子能谱与泵浦2激光场强的关系如图 4(a)所示. 激光参数: I0=1.0×1011 W·cm-2,I1=I3=4I0,λ1=848 nm,λ2=695 nm λ3=785 nm,τ=30 fs. 泵浦2激光场强为零时,光电子谱为双峰位于±R1/2的AT双分裂.泵浦2激光场引起双峰的一峰发生双分裂,从而导致三峰光电子谱.这与三/四态Λ-型体系的研究结果一致[16, 37].图 4(b)是三峰位置随泵浦2激光Rabi频率的变化图. 当泵浦2激光场较弱时(R2$ \ll $R1),AT分裂的外峰正比于R2/2 (图 4(b)中虚线所示). 当泵浦2激光场强较强时(R2$ \gg $R1) AT分裂的内峰位置接近零失谐位置(0.637eV),两边峰正比于R2.
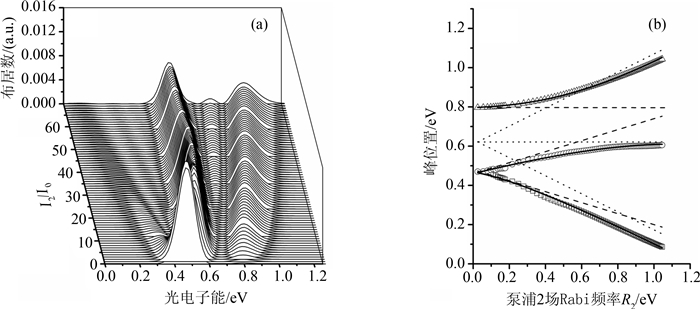 |
| 图4 (a)不同泵浦2激光场强的光电子能谱(Δ2=R1/2), (b) 光电子能谱谱峰位置与泵浦2场Rabi频率 R2的关系. (曲实线表示缀饰态理论结果. 虚直线和点直线分别表示R2$ \ll $R1和R2$ \gg $R1的渐近行为.) Fig. 4 (a) Photoelectron spectra for various Pump-2 laser intensities I2 with Δ2=R1/2, (b) Peak positions versus Pump-2 Rabi frequency R2 (Curves in solid lines show result using dressed-state formalism. Dashed straight lines and dotted straight lines indicate asymptotic behaviors for R2$ \ll $R1 and R2$ \gg $R1,respectively.) |
利用含时波包法研究了四态阶跃型K2分子光电子能谱的AT分裂.分别讨论了在泵浦2激光场共振,近共振区和远共振区三种情况下,泵浦2激光场强和波长对AT分裂的影响.
在共振区(λ2=695 nm),光电子谱为对称三分裂(峰高和相邻峰间距),AT间距随泵浦2场强增强而增大. 当泵浦2激光场强较弱时(R2$ \ll $R1),AT分裂正比于R1/2. 当泵浦2激光场强较强时(R2$ \gg $R1),AT分裂正比于R2/2.
在近共振区(695 nm≤λ2≤895 nm),光电子谱为不对称三分裂(峰高和相邻两峰间距),三峰中两边峰间距(0.370 eV)不因泵浦2波长改变而改变. 泵浦2波长增加,谱峰向低能方向移动.中间峰位移1/4Δ2,两边峰位移Δ2. 当泵浦2激光场偏离共振,三峰逐渐变为双峰. 近共振区和远共振区的临界点为Δ2=±R1/2(λ2=695 nm或者895 nm).
在远共振区(即λ2 < 695 nm和λ2 > 895 nm),光电子谱为不对称双峰(峰高),分裂间距不因泵浦2激光波长的改变而改变.泵浦2激光波长增加,双峰以相等位移量Δ2向低能方向移动.
在近共振区与远共振区的临界点λ2=695 nm,泵浦2激光场强为零时,光电子谱为双峰位于±R1/2的AT双分裂. 泵浦2激光场引起双峰的一峰发生双分裂,从而导致三峰光电子谱. 当泵浦2激光场较弱时(R2$ \ll $R1),AT分裂的外峰正比于R2/2. 当泵浦2激光场较强时(R2$ \gg $R1),AT分裂的内峰位置接近零失谐位置(0.637 eV),两边峰正比于R2.
| [1] | AUTLER S H, TOWNES C H. Stark effect in rapidly varying fields[J]. Physics Review, 1955, 100(2):703. |
| [2] | WOLLENHAUPT M, ASSION A, BAZHAN O, et al. Control of interferences in an Autler-Townes doublet:Symmetry of control parameters[J]. Physical Review A, 2003, 68(1):015401. |
| [3] | WOLLENHAUPT M, LIESE D, PRÄKELT A, et al. Quantum control by ultrafast dressed states tailoring[J]. Chemical Physics Letters, 2006, 419(1):184-190. |
| [4] | PENG Y, ZHENG Y J. Coherent optical spectroscopy of a single quantum dot using photon counting statistics[J]. Physical Review A, 2009, 80(4):043831. |
| [5] | WANG Z D, YANG S Y, LIU T T, et al. Effect of atomic density on propagation and spectral property of femtosecond Gaussian pulses[J]. Chinese Journal of Computational Physics, 2015, 32(1):75-85. |
| [6] | SUN Z G, LOU N Q. Autler-townes splitting in the multiphoton resonance ionization spectrum of molecules produced by ultrashort laser pulses[J]. Physical Review Letters, 2003, 91(2):023002. |
| [7] | YUAN K J, SUN Z G, CONG S L. Molecular photoelectron spectrum in ultrashort laser fields:Autler-Townes splitting under rotational and aligned effects[J]. Physical Review A, 2006, 74:043421. |
| [8] | YAO H B, ZHENG Y J. Autler-Townes splitting in photoelectron spectra of K2 molecule[J]. Chinese Physics B, 2012, 21(2):023302. |
| [9] | YAO H B, LI W L, ZHANG J, Peng M. Quantum control of K2 molecule in an intense laser field:Selective population of dressed states[J]. Acta Physica Sinica, 2014, 63(17):178201. |
| [10] | WEI C J, SUTER D, WINDSOR A S, et al. ac Stark effect in a doubly driven three-level atom[J]. Physical Review A, 1998, 58(3):2310-2318. |
| [11] | HAN D A, ZENG Y G, CHEN W C, et al. Sub- and super-luminal phenomena in a doubly driven four-level system[J]. Communications in Theoretical Physics, 2011, 55:671-675. |
| [12] | LIU Z B, FAN X J. Phase correlation in propagation effect of a Doppler broading quasi-Λ type four-level system[J]. Chinese Journal of Computational Physics, 2012, 29(6):881-890. |
| [13] | SADEGHI S M, MEYER J, RASTEGAR H. Laser-induced transparency and dark-line effects caused by three-wave mixing in atomic systems[J]. Physical Review A, 1997, 56(4):3097-3105. |
| [14] | YANG L J, ZHANG L S, ZHUANG Z H, et al. Spectral feature with sub-natural linewidth due to quantum interference in s four-level system[J]. Chinese Physics B, 2008, 17(6):2147-2151. |
| [15] | YANG L J, ZHANG L S, LI X L, et al. Autler-Townes effect in a strongly driven electromagnetically induced transparency resonance[J]. Physical Review A, 2005, 72(5):053801. |
| [16] | ZHANG L S, LI X L, WANG J, et al. Electromagnetically induced absorption and electromagnetically induced transparency in an optical-radio two-photon coupling configuration[J]. Acta Physica Sinica, 2008, 57(8):4921-4926. |
| [17] | DE ECHANIZ S R, GREENTREE A D, DURRANT, et al. Observation s of a driven V system probed to a fourth level in laser-cooled rubidium[J]. Physical Review A, 2001, 64(1):013812. |
| [18] | DUTTA B K, MAHAPATRA P K. Control of the spontaneous emission spectrum in a driven N-type atom by dynamically induced quantum interference[J]. Physica Scripta, 2009, 79:065402. |
| [19] | WANG D S,ZHENG Y J. Quantum interference in a four-level system of a 87Rb atom:effects of spontaneously generated coherence[J]. Physical Review A, 2011, 83(1):013810. |
| [20] | SANDHYA S N. The effect of atomic coherence on absorption in four-level atomic systems:an analytical study[J]. Journal of Physics B, 2007, 40:837-849. |
| [21] | MEIER C, ENGEL V. Interference structure in the photoelectron spectra obtained from multiphoton ionization of Na2 with a strong femtosecond laser pulse[J]. Physical Review Letters, 1994, 73(24):3207-3210. |
| [22] | MEIER C, ENGEL V, MANTHE U. An effective method for the quantum mechanical description of photoionization with ultrashort intense laser pulses[J]. Journal of Chemical Physics, 1998, 109(1):36-41. |
| [23] | HU W H, YUAN K J, HAN Y C, et al. Autler-Townes splitting in photoelectron spectrum of three-level Li2 molecule in ultrashort pulse laser fields[J]. Chinese Physics Letters, 2007, 24(6):1556-1559. |
| [24] | HU W H, YUAN K J, HAN Y C, et al. Three-peak Autler-Townes splitting in the photoelectron spectrum of Li2 molecules caused by femtosecond laser pulses[J]. International Journal of Quantum Chemistry, 2010, 110:1224-1234. |
| [25] | YAO H B, ZHENG Y J. Quantum control of a molecular system in an intense field via the selective population of dressed states[J]. Physical Chemistry Chemical Physics, 2011, 13:8900-8907. |
| [26] | BRIXNER T, KRAMPERT G, PFEIFER T, et al. Quantum control by ultrsfast polarization shaping[J]. Physical Review Letters, 2004, 92(20):208301. |
| [27] | SCHLESINGER M, MUDRICH M, STIENKEMEIER F, et al. Dissipative vibrational wave packet dynamics of alkali dimers attached to helium nanodroplets[J]. Chemical Physics Letters, 2010, 490:245-248. |
| [28] | MAGNIER S, AABERT-FRECON M, ALLOUCHE A R. Theoretical determination of highly excited states of K2 correlated adiabatically above K(4p)+K(4p)[J]. Journal of Chemical Physics, 2004, 121(4):1771-1781. |
| [29] | JRAIJ A, ALLOUCHE A R, MAGNIER S, et al. Theoretical spin-orbit structure of the alkali dimmer cation K2+[J]. Canadian Journal of Physics, 2008, 86(12):1409-1415. |
| [30] | JRAIJ A, ALLOUCHE A R, MAGNIER S, et al. Theoretical investigation of the Ωg,u(+/-) states of K2 dissociating adiabatically up to K(4p2P3/2)+K(4p2P3/2)[J]. Journal of Chemcial Physics, 2009, 130(24):244307. |
| [31] | DE VIVIE-RIEDLE R, KOBE R K, MANZ J, et al. Femtosecond study of multiphoton ionization processes in K2:pump-probe to control[J]. Journal of Physical Chemistry, 1996, 100:7789-7796. |
| [32] | ZHANG H, HAN K L, ZHAO Y, et al. A real time dynamical calculation of H2- photodissociation[J]. Chemical Physical Letters 1997, 271:204-208. |
| [33] | HU J, HAN K L, HE G Z. Correlation quantum dynamics between an electron and D2+ molecule with attosecond resolution[J]. Physical Review Letters, 2005, 95:123001. |
| [34] | LI X L, LIU H N, YANG Y. Influence of off-resonant coupling field on electromagnetically induced transparency and electromagnetically induced absorption in a closed Λ-shaped four-level system[J]. Acta Optica Sinica, 2011, 31(1):0102001. |
| [35] | ZHANG H B, KHADKA U, SSONG J P, et al. Measurement of ac-Stark shift by a two-photon dressing process via four-wave mixing[J]. Europhysics Letters, 2011, 93:23002. |
| [36] | ZHANG Y J, ZHANG Q Y, SONG Y Z, et al. Influence of femtosecond laser chirp on optical limiting and dynamical two-photon absorption of 4,4'-bis(di-n-butylamino) stilbene compounds[J]. Chinese Journal of Computational Physics, 2015, 32(1):65-74. |
| [37] | CARDIMONA D A, ALSING P M, MOZER H, et al. Interference effects in a three-level atom in a cavity beyond the weak-fiels approximation[J]. Physical Review A, 2009, 79(6):063817. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

