| 圆柱体外SGEMP的三维数值模拟 |
系统电磁脉冲(system-generated electromagnetic pulse,SGEMP)是核电磁脉冲的一个分类,是指X或γ射线与系统表面相互作用产生的电磁脉冲[1].由于系统电磁脉冲可直接在系统内部产生,无法使用电磁屏蔽的方法屏蔽,其对系统内电子部件的危害不可忽视[2],因此抗SGEMP效应是抗核加固的重点.
美国在20世纪70年代对SGEMP基本规律和特性进行了系统的理论分析和数值模拟研究,为至今仍在持续的SGEMP效应研究奠定了基础[3, 4, 5, 6, 7, 8],但受模拟发展水平的限制,所用程序大都局限于2维,对物理规律的认识有局限性.国内有很多涉及SGEMP的研究,但多侧重于各种专门效应的计算、模拟实验研究,对SGEMP基本规律和特性的研究较少[9, 10].
实际情况中,大多SGEMP效应属于3维问题,为了深入研究SGEMP的特性和规律,必须发展3维模拟能力.本文开发3维全电磁粒子模拟(PIC)程序,添加功能模块—用Monte Carlo方法计算SGEMP中电子发射的余弦角分布和指数能谱分布,作为校验,首先模拟具有旋转对称性的SGEMP模型——光电子由圆柱端面向外发射引起的SGEMP,并利用文献提供的由2维数值模拟得到的数据图表对计算模型的结果进行估算[11],将计算结果和估算结果对比,进而用该程序模拟研究圆柱体只有一半侧面向外发射的SGEMP模型.
1 圆柱端面向外发射的SGEMP 1.1 圆柱端面向外发射的SGEMP物理模型图 1是圆柱端面向外发射的SGEMP计算模型示意图.黑体谱X射线从一端沿轴向均匀入射到自由空间未接地的圆柱导体系统上,受照端面向外发射光电子,产生系统表面电流及系统周围的电磁场.圆柱体半径为10 cm,长度为20 cm.X射线的特征参量有注量φ(J·m-2)、特征温度T(eV)和时间脉冲,取正弦平方分布的时间脉冲
| $N\left(t \right)={N_0}{\sin ^2}\left[{\left({\pi t/2} \right)/\tau } \right],$ | (1) |
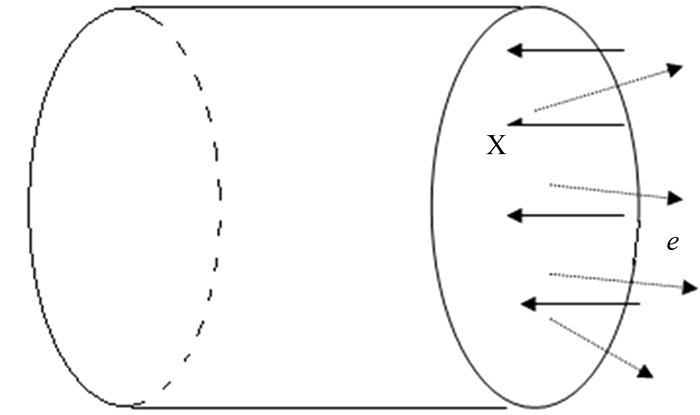 |
| 图1 模型示意图 Fig. 1 The model sketch |
其中N0为常数,τ为特征时间参量,0≤t≤2τ.
X射线各特征参量取值φ=4.0 J·m-2,T=2 keV,τ=25ns,Y=2×1012n·J-1=3.2×10-7C·J-1,其中,Y是光电产额,与X射线的特征温度和受照面材料有关.
1.2 SGEMP的规范变换及表面电场和侧面电流的估算圆柱体是SGEMP效应研究的典型几何结构,将其几何参数及黑体谱X射线的输入参数作规范化处理,可使解的通用性增强,文献中给出了半径为R,长度为2R的这类圆柱体的SGEMP输入参数的规范变换,得到特征输入参数[11];对于端面发射的外SGEMP,其响应结果主要由两个特征输出参数来描述:①是发射面上的垂直电场Ez;②是通过圆柱侧面中心的电流,与磁场关系为I=2πRHФ.文中将特征输入参数作为输入参数,跨越注入黑体谱X射线的线性区域和非线性区域对这类圆柱体端面发射的外SGEMP模型作了大量计算,并以图表形式给出了特征输出参数随各个输入参数的变化关系,图表中各个关系曲线都近似平滑,因此可用于对其包含及邻近的参数范围的外SGEMP产生的特征场量量级的估算和场随输入参数变化趋势的判定.
将本计算中的输入参数进行规范化处理,用文献中的图表估算SGEMP响应的两个特征场量[11],可估算出其表面电场的最大值约为EzR∈(103~104)V⇒Ez≈(104~105)V·m-1,侧面电流最大值约为I=2πRHϕ≈(0.1~1.0)A.
1.3 圆柱端面向外发射SGEMP的3维数值模拟 1.3.1 计算建模将光电子的特征参量作为输入参数,用3维全电磁粒子模拟程序进行模拟,由X射线的输入参数可以得到发射光电子的特征参量,受照面发射的总光电子数(正比于X射线注量)
| ${Q_{{\rm{TOT}}}}=YA\varphi,$ | (2) |
其中Q TOT是总发射电荷(C),A是发射面的面积(m2).
光电子的能谱(黑体谱X射线产生的光电子的能谱为指数谱)
| $dn/dE - {N_1}{{\rm{e}}^{ - E/{E_1}}},$ | (3) |
其中E是电子能量(keV), N1是常量,E1是表征射线能量的一个参数,对黑体谱射线可用黑体温度近似代替,但不是黑体温度本身.
黑体谱X射线垂直入射情况下产生的光电子的空间分布是余弦角分布,即发射电子数与cosθ成正比(θ
为电子发射方向与发射面法线的夹角).光电流的时间谱一般认为等同于X射线的时间谱.发射电子的时间函数由(1)式决定,取τ为25 ns,电子发射的总时间t为50 ns,总发射流可由(2)式得出,由(1)式积分等于(2)式可求得N0的值.计算空间大小: x=30 cm,y=30 cm,z=50 cm;半径为10 cm,长度为20 cm的圆柱体置于中间位置,采用笛卡尔坐标系,圆柱体轴线与z轴方向一致,圆柱轴线中点位于坐标原点,圆柱体的两端面分别位于z=10 cm和z=-10 cm的两平面上.空间各个方向网格大小都为2 mm,电子由右端面均匀向外发射,计算外边界设置理想吸收边界条件,即PML吸收边界,紧贴PML内侧设置电子吸收边界,发射的金属圆柱体构成了空间电磁波和电子吸收的内边界.
实现电子发射的余弦角分布和指数能谱分布是本计算建模的难点,为此在半开放式的程序中添加了相应的功能模块——用Monte Carlo随机抽样的方法实现电子发射的余弦角分布和指数能谱分布,余弦角分布的实现方法如下:由电子发射的余弦角分布得出电子分布密度函数为f(θ)=cosθ,于是积分分布函数是$F\left(\theta \right)=\int\limits_0^\theta {f\left(\theta \right)d\theta=\sin \theta } $,产生这个分布的方法为:第一步产生一个[0, 1]之间均匀分布的随机数r;第二步计算θ=arcsinr,然后Vz=V0cosθ,Vr=V0sinθ;最后产生[0,2π]之间均匀分布的角度α,令Vx=Vrcosα,Vy=Vrsinα.为了方便,这一段程序用python实现,然后导入到PIC程序中,指数能谱的实现方法类似. 1.3.2 计算结果图 2为初始时刻电子的实空间分布和沿z轴的相空间分布,由实空间分布图 2(a)可见,电子由端面向外发射,发射面各点电子均匀分布;由电子沿z轴的相空间分布图 2(b)、(c)可见,由于电子发射为余弦角分布,初始时刻电子不仅具有沿z轴的法向速度分量,同时具有沿横向的切向速度分量;由于发射的电子能谱为指数谱,所以轴向和横向电子动量分布都有一个较大的区间,且低动量的电子数要多于高动量的电子数.
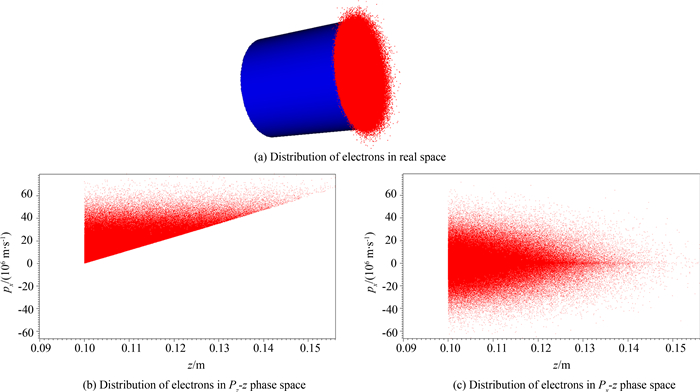 |
| 图2 初始时刻电子的实空间和相空间分布 Fig. 2 Distribution of electrons in real space and phase space at initial time |
图 3为发射面中点法向电场Ez和取y=0的切面侧面中点处横向磁场By的波形,由图中读出电场Ez最大值为21 kV·m-1,侧面磁场By最大值为9.0×10-7T,由于磁场分布具有旋转对称性,得出电流最大值为Imax=2πRHymax=0.45A,发射面电场和侧面电流最大值都与估算结果量级一致.
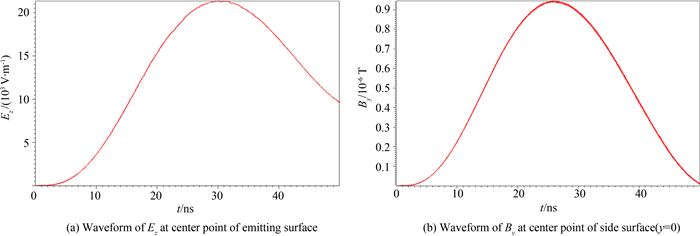 |
| 图3 电磁场波形图 Fig. 3 Electromagnetic field waveform |
由以上分析可见,本3维PIC程序计算所得物理图象符合预期,结果量级与文献一致,因此认为程序是可靠的,可以用来进行复杂SGEMP的3维模拟研究.
2 圆柱侧面向外发射的SGEMP当X射线平行于圆柱体端面照射时,受照面为圆柱体的半个侧面,因此只有这半个侧面向外发射光电子,应用本PIC程序研究这种情况下的3维SGEMP效应.为简化模型,假设受照面各点发射电子的能谱相同,仍为指数谱,空间分布仍为余弦角分布.取前面计算所用的X射线参数和同样尺寸的受照圆柱体,计算建模方法和前面大致相同,仍采用笛卡尔坐标系,因圆柱侧面是曲面,电子发射速度单独采用局部坐标系.
图 4给出不同时刻电子的空间分布,由图 4(a)可见,初始时刻在x大于0的半个侧面上各点电子均匀发射,图 4(b)显示5 ns时电子已到达吸收边界,由于切向速度及空间电荷力的作用电子沿横向扩散,由图 4(c)显示40 ns时电子已充满整个计算空间.
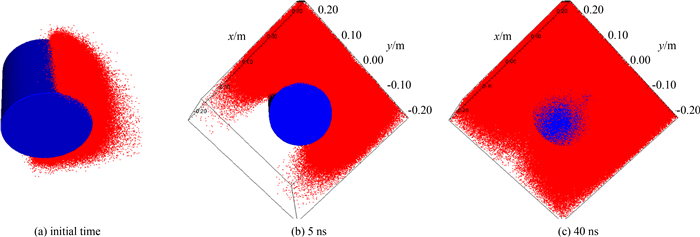 |
| 图4 不同时刻电子分布 Fig. 4 Distribution of electrons at several times |
图 5(a)为发射电流波形,电流在25 ns时取得最大值,约为3.3 A;图 5(b)为设在外边界x坐标值最大处且和x轴垂直的的吸收体所吸收的电流波形,其波形时间比发射电流时间略有延迟,吸收电流最大值约为0.38 A,另外发射电流还会被其余几个边界处的吸收体吸收;由于导体上正电荷的存在及空间电荷效应,电流还会被导体本身吸收,吸收电流波形如图 5(c)所示,最大值约为0.55 A.
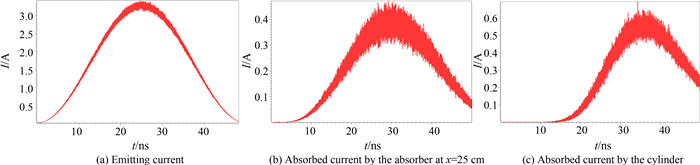 |
| 图5 发射电流及吸收电流波形 Fig. 5 Waveform of emitting current and absorbed current |
圆柱体为孤立导体,发射电子的同时导体上留下了等量的正电荷,空间电场由空间电子和导体上的正电荷共同激发.同时为保证导体为等势体,导体上的电荷需重新分布——电荷流动形成电流,也会影响空间磁场分布,因本模型是侧面发射,电流分布比较复杂.
对空间电磁场进行分析,可得出y=0的切面上电场最强,其中端面和侧面交界处电场最强,图 6给出43 ns时此切面上x=10.2 cm线上的电场幅度分布,电场幅度都达到10 kV·m-1量级,端面和侧面交界处电场最高为56 kV·m-1.图 7给出电场最强处即y=0的切面上端面和侧面交界处各电场分量的波形,由于电场由空间电子和导体上的正电荷共同激发,随着电子的发射,导体上积累的正电荷越来越多,电场也越来越强,约40 ns后电场才达到最大值,并且当发射电流结束时,由于导体上正电荷仍然存在,导体表面仍有很高的电场存在.Ex是该点的法向电场, Ez是轴向电场,都在10 kV·m-1量级,而由于两侧电荷产生的电场相互抵消,Ey幅度只有100 V·m-1量级.
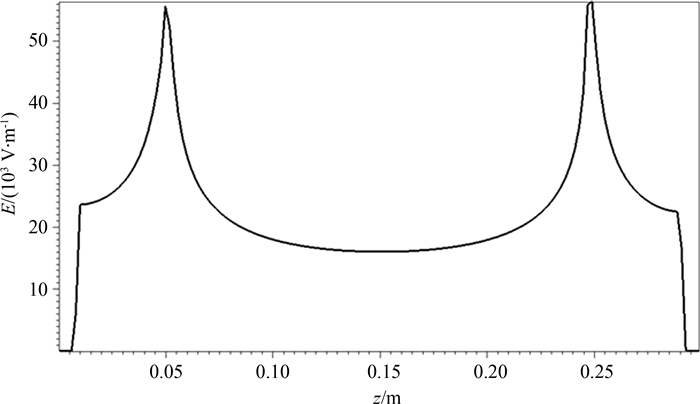 |
| 图6 t=43ns时y=0, x=10.2cm线上的电场分布 Fig. 6 Distribution of electric field on line of y=0, x=10.2cm |
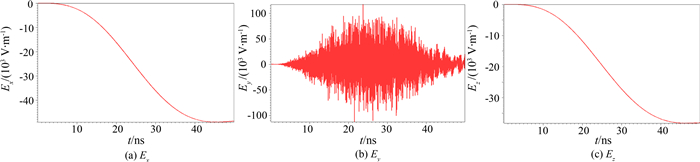 |
| 图7 坐标点x=10.2 cm, y=0, z=10.0 cm处的电场波形 Fig. 7 Waveform of electric field at point of x=10.2 cm, y=0, z=10.0 cm |
本模型中只有半个侧面发射,电流分布比较复杂,我们只分析空间磁场的情况,分析可得x=0的切面上磁场最强,磁场幅度都达到10-6T量级,其中端面和侧面交界处磁场最强,因磁场由电流产生,因此当电流取最大值时,即25 ns时磁场也达到最大值.图 8给出25 ns时此切面上y=10.2 cm线上的磁场幅度分布,端面和侧面交界处磁场最高,达3.0×10-6 T.图 9给出磁场最强处即x=0的切面上端面和侧面交界处各个磁场分量的波形,三个方向磁场分量都在10-6T量级,各磁场分量都在25 ns取得最大值,当发射电流结束时磁场消失.
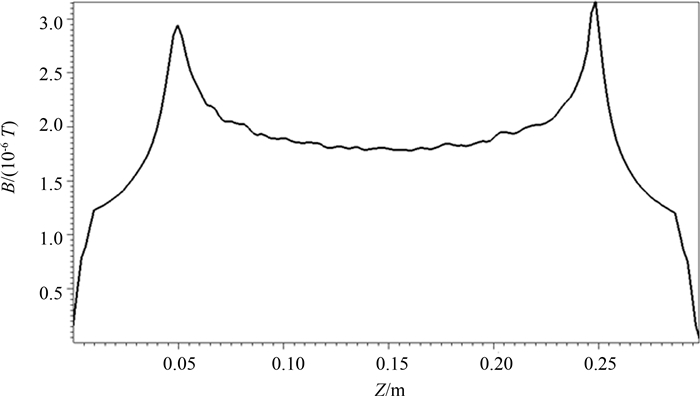 |
| 图8 t=25 ns时x=0, y=10.2cm线上的磁场分布 Fig. 8 Distribution of magnetic field on line of x=0, y=10.2 cm |
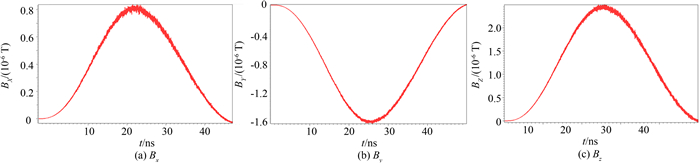 |
| 图9 坐标点x=0, y=10.2cm, z=10.0cm处的磁场波形 Fig. 9 Waveform of magnetic field at point of x=0, y=10.2cm, z=10.0cm |
开发利用半开放的3维PIC程序,模拟研究了具有旋转对称性的模型——圆柱端面向外发射的SGEMP模型,采用蒙卡方法在程序中添加功能模块实现光电子的余弦角分布和指数谱能量分布,并用文献提供的由2维模拟得到的图表对SGEMP的特征场量进行估算,模拟结果和估算结果量级一致,物理图象正确,验证了程序的可靠性.进而用该程序对圆柱体只有一半侧面向外发射的3维SGEMP进行模拟,对空间电磁场进行分析,得出导体侧面附近存在较强的电磁场,且电磁场在特定切面上的端面和侧面交界处最强,当发射电流为3.3 A时,电场强度最高可达56 kV·m-1,磁场高达3.0×10-6 T.
| [1] | WANG T C, HE Y H, WANG Y Z. Introduction to electromagnetic pulse[M]. Beijing:National Defense Industry Press, 2011:130-157. |
| [2] | CHENG Y H, ZHOU H, LI B Z, et al. Simulation of system-generated electromagnetic pulse caused by emitted photoelectron in cavity[J]. High Power Laser and Particle Beams, 2004, 16(8):1029-1032. |
| [3] | WENAAS E P, ROGERS S. Sensitivity of SGEMP to input parameters[J]. IEEE Trans on Nuclear Science, 1975, 22(6):2362-2367. |
| [4] | CARRON N J, LONGMIRE C L. Scaling behavior of the time-dependent SGEMP boundary layer[J]. IEEE Trans on Nuclear Science, 1978, 25(6):1329-1335. |
| [5] | HIGGINS D F, LEE K S H, MARIN L. System-generated EMP[J]. IEEE Trans on Antennas and Propagation, 1978, 26(1):14-22. |
| [6] | MICHAEL J S. Elementary external SGEMP model for system engineering design[J]. IEEE Trans on Nuclear Science, 1985, NS-32(6):4295-4299. |
| [7] | ZHOU H, LI B Z, WANG L J, et al. The calculation of SGEMP response in various ranges of X-ray fluence[J]. Chinese Journal of Computational Physics, 1999, 16(2):157-161. |
| [8] | CHEN Y S, HUA W. The simulation technique of system-generated electromagnetic pulse[J]. Chinese Journal of Computational Physics, 1992, 9(4):663-668. |
| [9] | ZHOU H, GUO H X, LI B Z, et al. Response of metal shell and cables to system generate electromagnetic pulse effects[J]. High Power Laser and Particle Beams, 16(5):645-648. |
| [10] | LI B Z, ZHOU H, GUO H X, et al. Research on system-generated electromagnetism pulse response for column model in metal cavity[J]. Atomic Energy Science and Technology, 2004, 38(5):448-451. |
| [11] | WOODS A J, WENNAS E P. Scaling laws for SGEMP[J]. IEEE Trans on Nuclear Science, 1976, 23(6):1903-1908. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
