| 含相变材料玻璃类围护结构传热系数分析 |
窗户等玻璃类围护结构是建筑中不可缺少的一部分,其传热系数直接影响建筑的热损失,而热损失不仅由室内外的温差所引起,还包括太阳辐照所引起的日射得热[1, 2, 3].含相变材料玻璃类围护结构可以调节日射得热,并通过相变蓄热改变其热损失.精确计算出此类围护结构的有效传热系数可为绿色建筑的发展提供理论基础[4, 5].
目前,对于玻璃类围护结构的传热系数研究一般仅考虑日射加热,忽略直接透射进入室内的太阳能对其传热系数计算的影响,对于两者耦合情况下的传热计算研究较少[6, 7].例如,丁勇等[6]分析夏季炎热条件下太阳辐射得热对搭载不同玻璃建筑的影响,考虑天空的散射以及玻璃对太阳辐射的反射吸收和透过,但仅通过日射得热值判断玻璃的传热效果;李宁等[7]研究玻璃隔热涂料对玻璃隔热性能的影响,分析涂料粘度、厚度、纳米粒径等因素对透光性的影响,仅以此判断涂料的隔热性能,但没有分析其传热系数对隔热性能的影响.
在建筑围护结构中填充相变材料可以有效调控太阳能[8, 9, 10, 11],其中,石蜡是在玻璃类围护结构中应用前景广阔的一类半透明相变材料,具有凝固点高,气候适应性强的优点[12, 13, 14].然而,由于太阳辐照度和围护结构内相变蓄热影响,含石蜡类玻璃类围护结构的有效传热系数与常规算法不同[15, 16, 17].
本文建立太阳能辐射加热下玻璃围护结构内的相变导热和辐射耦合传热模型,计算相变材料的辐射物性参数和室内外环境因素对含半透明相变材料玻璃围护结构的有效传热系数的影响.
1 数理模型与求解方法 1.1 物理模型与控制方程图 1为含半透明相变材料玻璃围护结构传热的一维模型.仅考虑沿玻璃围护结构厚度方向的温度变化,玻璃围护结构厚度为δ,玻璃与相变材料皆为纯吸收性介质,玻璃表面为半透明镜反射灰表面,满足Fresnel反射定律,不考虑相变材料内部的自然对流,忽略贴近相变材料层的两玻璃间表面辐射.
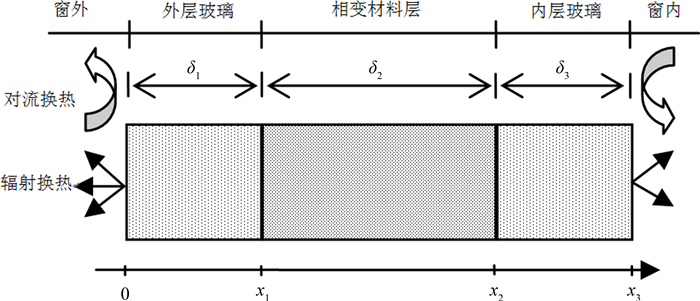 |
| 图1 物理模型 Fig. 1 Physical model |
太阳辐照作用下,玻璃围护结构内温度受有辐射源项的对流、辐射耦合边界控制,求解的方程如下:
玻璃围护结构内的能量方程
| $a\frac{{{\partial }^{2}}T}{\partial {{z}^{2}}}+\frac{{{\Phi }_{i}}}{\rho c}=0,$ | (1) |
其中,T为温度,Φi为太阳辐照能量,α为热扩散率,ρ为密度, c为比热.边界条件为:
在玻璃围护结构外表面x=0:
| $\begin{array}{l} - \lambda \frac{{{\rm{d}}T}}{{{\rm{d}}x}}=\sigma {\varepsilon _{{\rm{s,0}}}}{F_{{\rm{sky}}}}\beta \left({T_{{\rm{eg,o}}}^{\rm{4}} - T_{{\rm{sky}}}^4} \right)+\sigma {\varepsilon _{{\rm{s,0}}}}{F_{{\rm{sky}}}}\left({1 - \beta } \right)\left({T_{{\rm{eg,o}}}^{\rm{4}} - T_{{\rm{out}}}^{\rm{4}}} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sigma {\varepsilon _{{\rm{s,0}}}}{F_{{\rm{ground}}}}\left({T_{{\rm{eg,o}}}^{\rm{4}} - T_{{\rm{out}}}^{\rm{4}}} \right)+{h_{\rm{o}}}\left({{T_{{\rm{eg,o}}}} - {T_{{\rm{out}}}}} \right); \end{array}$ | (2) |
在玻璃围护结构内表面x=δ:
| $ - \lambda \frac{{{\rm{d}}T}}{{{\rm{d}}x}}=\sigma {\varepsilon _{{\rm{ig,i}}}}\left({T_{{\rm{in}}}^{\rm{4}} - T_{{\rm{ig,i}}}^4} \right)+{h_{\rm{i}}}\left({{T_{{\rm{in}}}} - {T_{{\rm{ig,o}}}}} \right)$ | (3) |
其中, σ是玻尔兹曼常量,εig,i、 εs,o分别为围护结构内、外表面的发射率,Fsky、 Fground分别为围护结构外表面与天空、外部环境的视角因数,β为天空与空气辐射之间的衰减因子,计算方法参照文献[18].Teg,o、Tout与Tsky分别为围护结构外表面温度、外界环境温度与天空温度,Tsky的计算方法参照文献[18].Tig,i、Tin分别围护结构内表面温度与房屋内空气温度.玻璃围护结构外表面与空气间的对流换热系数[18]
| ${h_{\rm{o}}}=\max \left({1.52{{\left| {\Delta T} \right|}^{1/3}},5.62+3.9v} \right);$ | (4) |
玻璃围护结构内表面与空气的对流换热系数为[18]
| ${h_{\rm{i}}}={\left\{ {{{\left[{1.5{{\left({\Delta T/H} \right)}^{1/4}}} \right]}^6}+{{\left[{1.23{{\left({\Delta T} \right)}^{1/3}}} \right]}^6}} \right\}^{1/6}},$ | (5) |
其中,ΔT为围护结构内表面与空气之间的温差, H为围护结构离地高度.
1.2 数值方法与验证采用控制容积法、隐式格式对偏微分方程进行离散,采用TDMA算法迭代求解[19, 20].太阳光透过相变玻璃围护结构进入室内,需经过两层玻璃与相变材料,利用布格尔定律求解太阳光在玻璃幕墙内部的源项为
| ${\Phi _i}=\left({{I_{i - 1 \to i}}+{I_{i+1 \to i}}} \right)- \left({{I_{i \to i+1}}+{I_{i \to i - 1}}} \right)n_i^2/\Delta {x_i},$ | (6) |
其中, Ii-1→i表示沿控制体i-1方向传到控制体i边界处的辐射强度值,ni与△xi分别为控制体i的折射率与体积.
相变材料在受热过程中会释放相变潜热,在此不独立求解相变层内的能量方程,根据潜热比热值利用差值法求解相变过程中的比热,实现对温度值的求解,具体计算方法如文献[18]所示.
通过与实验结果对比验证数值模型的可靠性.如图 2所示,此实验为测量太阳辐照作用下石蜡玻璃幕墙内的稳态温度场和透光率.实验过程将6 mm石蜡层密封装在两层厚4 mm,面积为500 mm×400 mm的浮法玻璃内,利用T型热电偶测量温度值,采用TBQ-4-5型辐射热流计测量透过玻璃幕墙后的辐照强度.光源采用TPM-PD型人工太阳模拟发射器,可通过控制箱调节模拟器的辐照强度.利用空调控制室内温度恒定.实验时当各仪器参数在10分钟内浮动小于2%认为实验结果达到稳态.实验中设定空气温度为Tk=295 K,太阳模拟发射器的辐照强度qr=100 W·m-2、 300 W·m-2、 500 W·m-2、 700 W·m-2、 900 W·m-2.
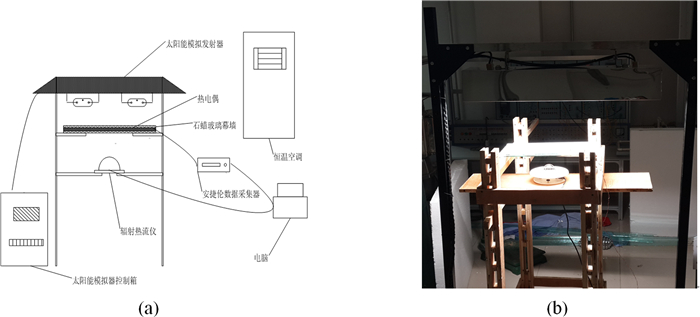 |
| 图2 实验系统图 Fig. 2 Schematic experimental system |
数值计算时将此问题简化为一维模型,只考虑沿石蜡玻璃幕墙厚度方向的热量传递.浮法玻璃的物性参数分别为ρb=2 500 kg·m-3,λb=0.96 W·(mK)-1,Cp,b=840 J·(kg·K)-1,石蜡材料的物性参数取自文献[19].玻璃幕墙上下表面与室内空气间存在热面朝上、热面朝下两种情况的自然对流换热,与周围墙壁之间存在辐射换热,计算时认为房间内墙壁温度与空气温度相同.
结果如图 3所示,其中实心符号表示数值模拟结果,空心符号表示实验结果.总体来说,就温度场而言,数值结果与实验值相比,幕墙上表面平均相对误差为2.4%,下表面的平均相对误差为3.3%.就透过率而言,数值结果与实验值相比,相对误差为20.2%.透过率的误差相对较大,这主要来源于qr≤300 W/m2时,因为实验中选取的石蜡种类虽然与文献[19]中选取相同,但由于实验过程中要确保支架不被太阳能模拟器烤化,相变模拟幕墙设置在离模拟器400 mm处,所以当它功率较小时,实际发射到幕墙上表面的能量可能很小,导致石蜡几乎呈固体状态,与模拟值相差较大,这从上下表面的温度场也能看出.除去前两个点,透过率的误差仅为6.7%.说明本文所采用的数值模型是可靠的.
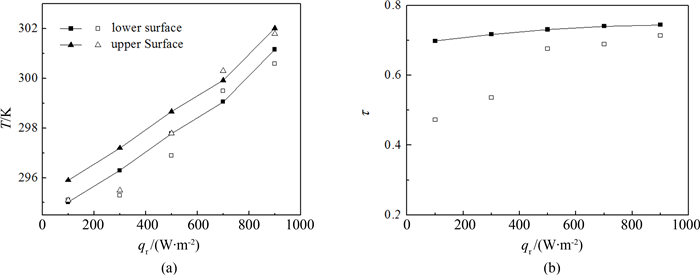 |
| 图3 数值解与实验结果 Fig. 3 Numerical and experimental result |
当玻璃围护结构两侧有温差时,热量就会从温度高的一侧通过构件传递到温度低的一侧.其间,在构件两侧温差为1度时,单位时间、通过构件单位面积所传递的热量叫总传热系数,即U值.对玻璃围护结构而言,其传热可区分为两个部分,一是经过介质透过的太阳辐照传热,二是由室内外温差引起的传热.
太阳辐照传热主要通过辐射热流和当量温差来计算
| $U={q_{\rm{t}}}/\Delta {T^*},$ | (7) |
其中,qt为透入室内的太阳辐照热流,△T*为由太阳辐照作用所引起的当量温差.
对室内外温差引起的传热,主要考虑三个方面:①玻璃围护结构外表面与室外环境间的辐射与对流;②玻璃围护结构内部的热传导;③玻璃围护结构内表面与室内环境间的辐射与对流.
| $\frac{1}{U}=\frac{1}{{{h_{\rm{o}}}}}+\sum\limits_{i=1}^n {\frac{{{{\rm{\delta }}_i}}}{{{{\rm{\lambda }}_i}}}}+\frac{1}{{{h_{\rm{i}}}}},$ | (8) |
其中,n=1,2,3,…,λi与δi分别为第i层材料的导热系数和厚度,ho,hi分别为室外、室内环境与玻璃围护结构表面的对流、辐射耦合作用的传热系数,计算方法按照文献[21].
要计算太阳辐照作用下玻璃围护结构内部的总传热系数U值,需要将以上两部分传热效果叠加.由于计算太阳辐照传热部分时,当量温差△T*无法确定,于是利用公式
| $U=q/\left({{T_{{\rm{in}}}} - {T_{{\rm{out}}}}} \right),$ | (9) |
其中,q为太阳辐照作用下玻璃围护结构内部的稳态传热热流,q=qt+qc,qc为内部的导热热流.
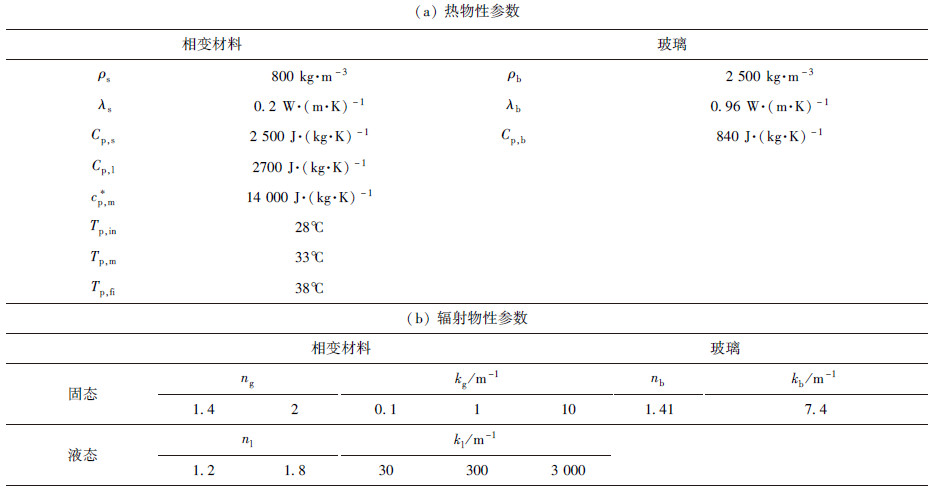
3 结果与讨论通过选取折射率n、吸收系数k,分析玻璃围护结构的隔热效果,计算参数如表 1.三层材料的厚度δ1、 δ2、δ3分别为0.008 m、0.015 m、0.008 m.边界条件中室内温度Ti、室外温度Tou分别为300 K、290 K与293 K、253 K,风速v为3 m·s-1,太阳辐照度qr分别取为100 W·m-2,300 W·m-2,500 W·m-2,700 W·m-2,900 W·m-2.
| 表1 玻璃与相变材料的物性参数 Table 1 Physical parameters of glass and PCM |
 |
| 点击放大 |
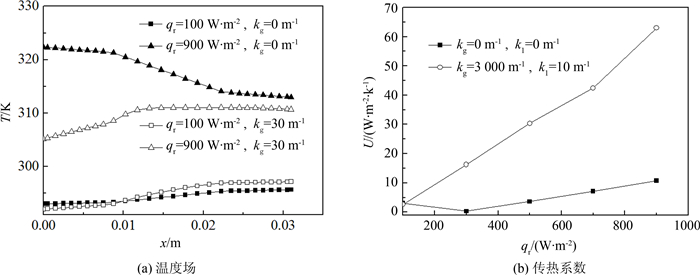
图 4为玻璃围护结构的半透明性对内部温度和传热系数的影响.计算条件qr分别为100 W·m-2、 300 W·m-2、 500 W·m-2、 700 W·m-2与900 W·m-2,kg、 kl分别为30 m-1、 0.1 m-1与0、0, ng、nl分别为1.4、 2.
 |
| 图4 玻璃围护结构的半透明性对传热系数的影响 Fig. 4 Influence of semitransparent property of a PCM-glazed unit on heat transfer coefficient |
如图所示,无论是否考虑玻璃围护结构的半透明性,U值随着qr的增强而增大.但不考虑玻璃围护结构半透明性时, qr为300 W·m-2时U值比100 W·m-2时更小,原因在于与qr较大时相比, qr较小时太阳能的供热负荷小于房间的散热负荷,导致热量由房间内部向房间外部传递.相比而言,考虑玻璃围护结构的半透明性时,玻璃围护结构内部的温度分布更均匀,U值更大.在各太阳辐照热流情况下,考虑半透明性时,传热比不考虑半透明性时U值平均高出25.98 W·m-2·K-1,说明在计算玻璃围护结构的U值时,不考虑其半透明性会产生很大误差.除此之外,是否考虑半透明性对玻璃围护结构内的温度和U值的影响情况不一致,例如,不考虑半透明性时玻璃围护结构内的温度值比考虑其半透明性时平均高8.29 K,而U值反而低52.25 W·m-2·K-1.由于考虑玻璃围护结构的半透明性时,太阳辐照会使其内部的相变材料融化、吸收系数降低,热阻减小,传热量增大.同时,部分太阳辐照热流没透过玻璃进入室内,导致其内部温度相对较低.
图 5为三种吸收系数和两种折射率情况下,玻璃围护结构的U值.其中,实心符号表示ng、 nl分别为1.4、 1.2,空心符号表示ng、nl分别为2、 1.8.当qr≤300 W·m-2时,吸收系数越小,折射率越大时,U值越大;当 qr>300 W·m-2时,折射率对U值的影响仍保持原趋势,但吸收系数对U值的影响较为复杂.原因是当qr>300 W·m-2时,此三种吸收系数的相变材料都会出现不同程度的融化,U值还会间接受到液相率与透光率等因素的影响.
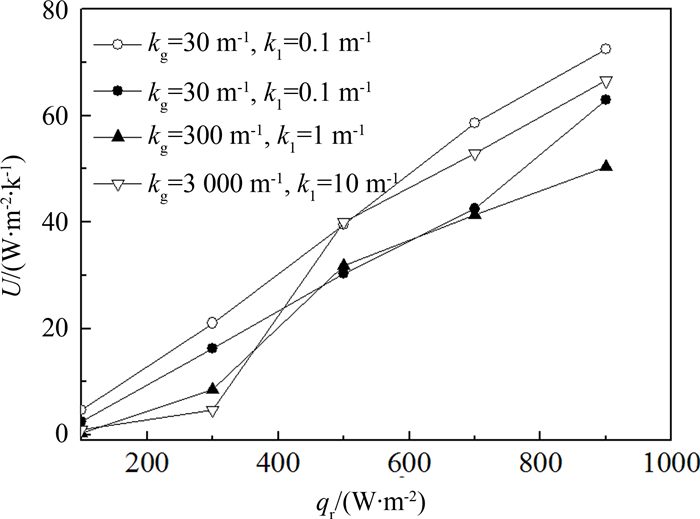 |
| 图5 吸收系数和折射率对传热系数的影响 Fig. 5 Influence of absorption coefficient and refractive index on heat transfer coefficient |
图 6为环境条件对玻璃围护结构U值的影响.其中,ng、 nl分别为1.4、 1.2,实心符号表示Ti、 Tou分别为300 K、 290 K时的情况;空心符号表示Ti、 Tou分别为293 K、 253 K时的情况.如图所示,在两种吸收系数下(kg、 kl分别为30 m-1、0.1 m-1与3 000 m-1、 10 m-1),除qr=100 W·m-2外,高温情况(Ti、 Tou分别为300 K、290 K)的U值都比低温时大.kg、 kl分别为30 m-1、 0.1 m-1时,高温情况的U值比低温时平均高出2.8 W·m-2·K-1;而当kg、 kl分别为3 000 m-1、 10 m-1时,高温情况的U值比低温时平均高出25.2 W·m-2·K-1.说明外界环境因素对玻璃围护结构的U值也有一定影响,且吸收系数越大,影响越明显.
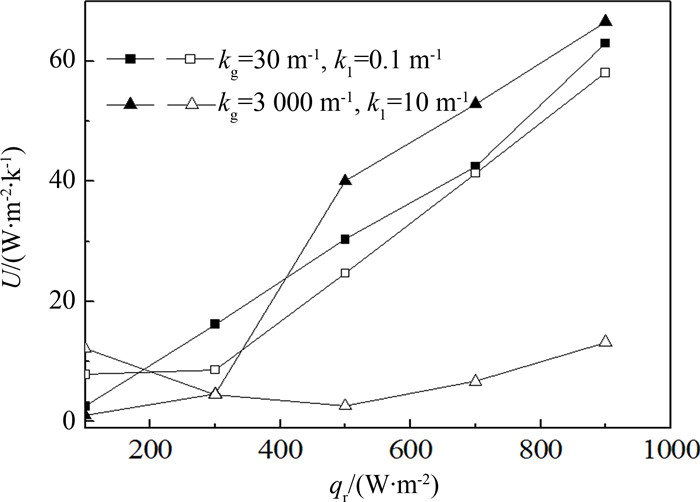 |
| 图6 室内外环境对传热系数的影响 Fig. 6 Influence of internal and external environment on heat transfer coefficient |
利用控制容积法及布格尔定律,分析稳态过程中,相变材料的吸收系数、折射率以及室内外的环境条件对玻璃围护结构U值的影响,得出如下结论:
1) 考虑玻璃围护结构的半透明性对其U值影响很大,是否考虑半透明性对玻璃围护结构内的温度和传热系数的影响也不一致.
2) 相变材料的吸收系数和折射率对太阳辐照作用下玻璃围护结构的U值都有影响.但并不是吸收系数越小,U值越大,还受相变材料融化后的液相率与透光率等因素的影响.
3) 室内外环境条件对玻璃幕墙的U值有一定影响,且吸收系数越大,影响越明显.
| [1] | 林涛,刘茜. 玻璃组合方式对双层幕墙通风和传热的影响[J].建筑科学,2014,30(9):93-97. |
| [2] | 季亮,谭洪卫,郑淑晶.透明隔热玻璃涂料的建筑节能潜力分析[J].建筑科学,2013,29(4):6-10. |
| [3] | 叶宏,葛新石,张永峰.整体式太阳热水器在寒冷气候条件下的冻结厚度与热损系数U值及水层深度的关系[J]. 太阳能学报, 2002, 23(3):270-276. |
| [4] | POMIANOWSKI M, HEISELBERG P, ZHANG Y P. Review of thermal energy storage technologies based on PCM application in buildings[J]. Energy and Buildings, 2013, 67:56-69. |
| [5] | SOARES N, COSTA J J, GASPAR A R. Review of passive PCM latent heat thermal energy storage systems towards buildings' energy efficiency[J]. Energy and Buildings, 2013, 59:82-103. |
| [6] | 丁勇,刘旭,丁正辽. 不同玻璃对夏季炎热地区室内太阳辐射得热的影响分析[J]. 太阳能学报, 2014, 35(1):177-182. |
| [7] | 李宁,孟庆林. 玻璃隔热涂料隔热性能的影响因素研究[J]. 太阳能学报, 2013, 34(5):810-813. |
| [8] | ISMAIL A R, SALINAS C T, HENRIQUEZ J R. Comparison between PCM filled glass windows and absorbing gas filled windows[J]. Energy and Buildings, 2008, 40:710-719. |
| [9] | GOIA F, BIANCO L, CASCONE Y. Experimental analysis of an advanced dynamic glazing prototype integrating PCM and thermotropic layers[J]. Energy Procedia, 2014, 48:1272-1281. |
| [10] | CARLOS J S, CORVACHO H. Evaluation of the performance indices of a ventilated double window through experimental and analytical procedures:SHGC-values[J]. Energy and Buildings, 2015, 86:886-897. |
| [11] | SILVA T, VICENTE R, RODRIGUES F. Development of a window shutter with phase change materials:Full scale outdoor experimental approach[J]. Energy and Buildings, 2015, 88:110-121. |
| [12] | CHOW Tin-Tai, LI C Y, LIN Z. Thermal characteristics of water-flow double-pane window[J]. International Journal of Thermal Sciences, 2011, 50(2):140-148. |
| [13] | IZQUIERDO-BARRIENTOS M A, BELMONTE J F, Rodríguez-Sánchez D. A numerical study of external building walls containing phase change materials (PCM)[J]. Applied Thermal Engineering,2012, 47:73-85. |
| [14] | EVOLA G, MARLETTA L, SICURELLA F. A methodology for investigating the effectiveness of PCM wallboards for summer thermal comfort in buildings[J]. Building and Environment, 2013, 59:517-527. |
| [15] | 杨昭,郁文红,张甫仁. 建筑物冬季太阳辐射得热分析[J]. 太阳能学报, 2005, 26(1):104-109. |
| [16] | 吴彦廷,周国兵,杨勇平. 太阳能相变蓄热集热墙二维非稳态模型及分析[J]. 太阳能学报, 2012, 33(6):948-952. |
| [17] | 李德坚,唐轩,殷志强. 温室太阳能供暖[J]. 太阳能学报, 2002, 23(5):557-563. |
| [18] | GOIA F, PERINO M, HAASE M. A numerical model to evaluate the thermal behaviour of PCM glazing system configurations[J]. Energy and Buildings, 2012, 54:141-153. |
| [19] | GOWREESUNKER B L, STANKOVIC S B, TASSOU S A. Experimental and numerical investigations of the optical and thermal aspects of a PCM-glazed unit[J]. Energy and Buildings, 2013, 61:239-249. |
| [20] | SUN F X,LIU C Y,XIA X L.Effect of solar radiation on evaporation of still water surface[J]. Chinese Journal of Computational Physics,2014,31(6):699-705. |
| [21] | LIU M Z,WITTCHEN K B,HEISELBER P K.Development and sensitivity study of a simplified and dynamic method for double glazing façade and verified by a full-scale façade element[J]. Energy and Buildings, 2014, 68:432-443. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

