| 正交各向异性材料切口尖端热弹奇性特征分析 |
切口尖端由于几何或材料突变而产生奇异应力场,严重影响构件的力学性能.况且,含V形切口构件承受的荷载往往复杂多样,不仅承受机械荷载,有时还要承受热荷载.计算热机荷载联合作用下切口尖端的奇性特征状况,可为评价含切口构件的力学性能提供重要依据.
傅向荣等[1]通过解析试函数法分析了各向同性单材料平面切口的弹性应力奇性指数.许金泉等[2]利用Goursat公式得到了双材料界面端附近的奇异应力场解析值.除了解析法,张明等[3]采用边界元法分析了双材料界面裂纹应力强度因子.郑百林等[4]研究了双材料反平面问题界面端奇异应力场.葛仁余等[5]研究了二维线弹性裂纹扩展.程长征等[6]研究了单相材料、双相材料及止于异质界面的反平面切口的奇异性.Prasad等[7]采用双重边界元法分析了热荷载对应力强度因子值的影响.Caicedo等[8]将边界元法与Williams展开式相结合计算了平面裂纹的应力强度因子.Yosibash等[9]从渐近型的温度场和椭圆齐次方程的弱形式出发,采用有限元法得到一个线性矩阵特征方程,求解了平面弹性奇异应力场特征解问题.平学成等[10]基于有限元特征分析法分析了热机载荷下夹杂角端部的应力场.实验研究方面,Ayatollari等[11]采用光弹实验研究了双材料V形切口的应力强度因子.纵观这些文献,均是单独进行应力奇异性或者热流奇异性分析,没有同时考虑切口尖端的应力和热流奇异性.
本文考虑正交各向异性平面V形切口,通过引入切口尖端物理场的渐近级数展开式,将平衡方程转化为关于奇异性指数的特征微分方程组,联合分析切口尖端的应力和热流奇异性.
1 切口热弹奇性特征方程考虑如图 1所示正交各向异性材料的平面V形切口,在切口尖端定义笛卡尔坐标系(oxy)、极坐标系(orθ)、材料主轴系(o12).其中,x轴与切口平分线重合,材料主轴相对笛卡尔坐标系旋转角为φ.在材料主轴系(o12)下,正交各向异性材料平面应力问题的热弹本构关系为
| $\left[\begin{array}{l} {\varepsilon _1}\\ {\varepsilon _2}\\ {\gamma _{12}} \end{array} \right]{\rm{=}}\left[{\begin{array}{*{20}{c}} {{s_{11}}}&{{s_{12}}}&0\\ {{s_{21}}}&{{s_{22}}}&0\\ 0&0&{{s_{33}}} \end{array}} \right]\left[\begin{array}{l} {\sigma _1}\\ {\sigma _2}\\ {\tau _{12}} \end{array} \right]+\left[\begin{array}{l} {\alpha _1}\\ {\alpha _2}\\ 0 \end{array} \right]T,$ | (1) |
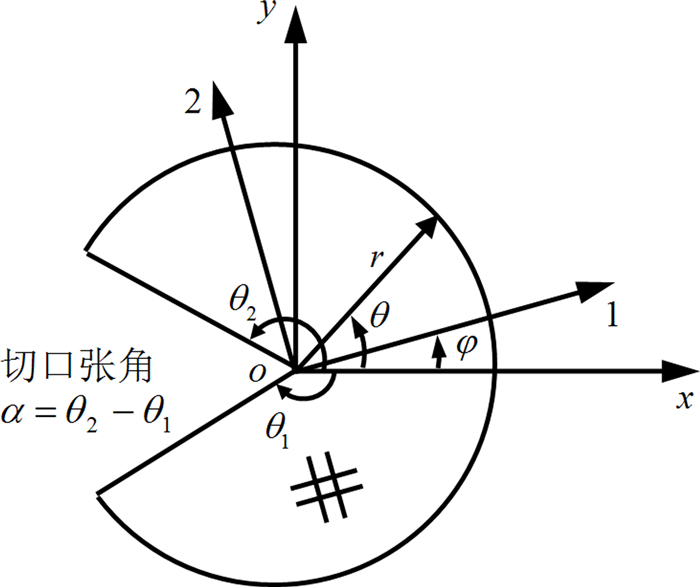 |
| 图1 切口尖端坐标系 Fig. 1 Coordinate systems originated from V-notch tip |
式中ε1,ε2,γ12为应变分量;σ1,σ2,τ12为应力分量;T为温度;s11=1/E1,s22=1/E2,s12=s21=-ν21/E1,s33=1/G12,其中,E1,E2为弹性模量,ν21,G12分别为泊松比、剪切模量;α1,α2为热膨胀系数.
在极坐标系(orθ)下材料的本构方程可由式(1)进行坐标变换为
| $\left[\begin{array}{l} {\sigma _r}\\ {\sigma _\theta }\\ {\tau _{r\theta }} \end{array} \right]=\left[{\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&{{Q_{13}}}\\ {{Q_{21}}}&{{Q_{22}}}&{{Q_{23}}}\\ {{Q_{31}}}&{{Q_{32}}}&{{Q_{33}}} \end{array}} \right]\left[\begin{array}{l} {\varepsilon _r}\\ {\varepsilon _\theta }\\ {\gamma _{r\theta }} \end{array} \right] - \left[\begin{array}{l} {P_1}\\ {P_2}\\ {P_3} \end{array} \right]T,$ | (2) |
式中Qij,Pi(i,j=1,2,3)分别为刚度系数和热膨胀系数与关于(θ,φ)的三角函数的乘积.另外,在极坐标系下应变与位移的关系为
| $\begin{array}{l} {\varepsilon _r}=\frac{{\partial {u_r}}}{{\partial r}},\\ {\varepsilon _\theta }=\frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }}+\frac{{{u_r}}}{r},\\ {r_{r\theta }}=\frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }}+\frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}. \end{array}$ | (3) |
将式(3)代入式(2),可以得到正交各向异性材料在热机荷载作用下的应力分量
| $\begin{array}{l} {\sigma _r}={Q_{11}}\frac{{\partial {u_r}}}{{\partial r}}+{Q_{12}}\left({\frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }}+\frac{{{u_r}}}{r}} \right)+{Q_{13}}\left({\frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }}+\frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}} \right)- {P_1}T,\\ {\sigma _\theta }={Q_{21}}\frac{{\partial {u_r}}}{{\partial r}}+{Q_{22}}\left({\frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }}+\frac{{{u_r}}}{r}} \right)+{Q_{23}}\left({\frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }}+\frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}} \right)- {P_2}T,\\ {\tau _{r\theta }}{Q_{31}}\frac{{\partial {u_r}}}{{\partial r}}+{Q_{32}}\left({\frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }}+\frac{{{u_r}}}{r}} \right)+{Q_{33}}\left({\frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }}+\frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}} \right)- {P_3}T. \end{array}$ | (4) |
另一方面,主轴系下热流h1,h2与温度梯度əT/əx1,əT/əx2的关系为
| $\left[\begin{array}{l} {h_1}\\ {h_2} \end{array} \right]=- \left[{\begin{array}{*{20}{c}} {{k_{11}}}&0\\ 0&{{k_{22}}} \end{array}} \right]\left[\begin{array}{l} \partial T/\partial {x_1}\\ \partial T/\partial {x_2} \end{array} \right],$ | (5) |
式中k11,k22表示材料主轴方向上的导热系数.将式(5)通过坐标变换,可以得到极坐标系下热流与温度梯度的关系式
| $\left[\begin{array}{l} {h_r}\\ {h_\theta } \end{array} \right]=- \left[{\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}\\ {{k_{21}}}&{{k_{22}}} \end{array}} \right]\left[\begin{array}{l} \partial T/\partial r\\ {r^{ - 1}}\partial T/\partial \theta \end{array} \right],$ | (6) |
其中,hr,hθ分别为径向和周向热流,Kij(i,j=1,2)为导热系数k11,k22与关于(θ,φ)的三角函数的乘积.
将式(4)和式(6)代入如下的应力和热流平衡方程
| $\begin{array}{l} \frac{{\partial {\sigma _r}}}{{\partial r}}+\frac{1}{r}\frac{{\partial {\tau _{r\theta }}}}{{\partial \theta }}+\frac{{{\sigma _r} - {\sigma _\theta }}}{r}=0,\\ \frac{1}{r}\frac{{\partial {\sigma _\theta }}}{{\partial \theta }}+\frac{{\partial {\tau _{r\theta }}}}{{\partial r}}+\frac{{2{\tau _{r\theta }}}}{r}=0,\\ \frac{{\partial {h_r}}}{{\partial r}}+\frac{1}{r}\frac{{\partial {h_\theta }}}{{\partial \theta }}+\frac{{{h_r}}}{r}=0, \end{array}$ | (7) |
化简后有
| $\begin{align} & r{{Q}_{11}}\frac{{{\partial }^{2}}{{u}_{r}}}{\partial {{r}^{2}}}+\frac{{{Q}_{33}}}{r}\frac{{{\partial }^{2}}{{u}_{r}}}{\partial {{\theta }^{2}}}+\left( {{Q}_{31}}+{{Q}_{13}} \right)\frac{{{\partial }^{2}}{{u}_{r}}}{\partial r\partial \theta }+\left( {{Q}_{11}}+{{Q}_{12}}-{{Q}_{21}}+Q_{31}^{'} \right)\frac{\partial {{u}_{r}}}{\partial r}+ \\ & \frac{1}{r}\left( {{Q}_{32}}-{{Q}_{23}}+Q_{^{33}}^{'} \right)\frac{\partial {{u}_{r}}}{\partial \theta }+r{{Q}_{13}}\frac{{{\partial }^{2}}{{u}_{\theta }}}{\partial {{r}^{2}}}+\frac{{{Q}_{32}}}{r}\frac{{{\partial }^{2}}{{u}_{\theta }}}{\partial {{\theta }^{2}}}+\left( {{Q}_{33}}+{{Q}_{12}} \right)\frac{{{\partial }^{2}}{{u}_{\theta }}}{\partial r\partial \theta }+ \\ & \left( Q_{^{33}}^{'}-{{Q}_{23}} \right)\frac{\partial {{u}_{\theta }}}{\partial r}+\frac{1}{r}\left( Q_{^{32}}^{'}-{{Q}_{22}}-{{Q}_{33}} \right)\frac{\partial {{u}_{\theta }}}{\partial \theta }+\frac{1}{r}\left( Q_{^{32}}^{'}-{{Q}_{22}} \right){{u}_{r}}+\frac{1}{r}\left( {{Q}_{23}}-Q_{^{33}}^{'} \right){{u}_{\theta }}- \\ & {{P}_{1}}r\frac{\partial T}{\partial r}-\left( {{P}_{1}}-{{P}_{2}} \right)T-{{P}_{3}}\frac{\partial T}{\partial \theta }-P_{3}^{'}T=0, \\ & r{{Q}_{31}}\frac{{{\partial }^{2}}{{u}_{r}}}{\partial {{r}^{2}}}+\frac{{{Q}_{23}}}{r}\frac{{{\partial }^{2}}{{u}_{r}}}{\partial {{\theta }^{2}}}+\left( {{Q}_{21}}+{{Q}_{33}} \right)\frac{{{\partial }^{2}}{{u}_{r}}}{\partial r\partial \theta }+\left( Q_{21}^{'}+{{Q}_{32}}+2{{Q}_{31}} \right)\frac{\partial {{u}_{r}}}{\partial r}+ \\ & \left( Q_{23}^{'}+{{Q}_{33}} \right)\frac{\partial {{u}_{\theta }}}{\partial r}+\frac{1}{r}\left( {{Q}_{32}}-{{Q}_{23}}+Q_{22}^{'} \right)\frac{\partial {{u}_{\theta }}}{\partial \theta }+\frac{1}{r}\left( {{Q}_{32}}+Q_{22}^{'} \right){{u}_{r}}-\frac{1}{r}\left( {{Q}_{33}}+Q_{23}^{'} \right){{u}_{\theta }}- \\ & p{{'}_{2}}T-{{p}_{2}}\frac{\partial T}{\partial \theta }-{{P}_{3}}r\frac{\partial T}{\partial r}-2{{P}_{3}}T=0, \\ & r{{K}_{11}}\frac{{{\partial }^{2}}T}{\partial {{r}^{2}}}+\frac{1}{r}{{K}_{22}}\frac{{{\partial }^{2}}T}{\partial {{\theta }^{2}}}+\left( {{K}_{12}}+{{K}_{21}} \right)\frac{{{\partial }^{2}}T}{\partial r\partial \theta }+{{K}_{11}}\frac{\partial T}{\partial r}+K_{21}^{'}\frac{\partial T}{\partial r}+K_{22}^{'}\frac{\partial T}{\partial \theta }=0, \\ \end{align}$ | (8) |
其中,(…)′表示对坐标θ的一阶导数.
将切口尖端的位移和温度场按如下级数渐近展开[9]
| $\begin{array}{l} {u_r}=\sum\limits_{k=1}^N {{A_k}{r^{\lambda k}}{{\tilde u}_{rk}}\left({{\lambda _k},\theta } \right)},\\ {u_\theta }=\sum\limits_{k=1}^N {{A_k}{r^{\lambda k}}{{\tilde u}_{\theta k}}\left({{\lambda _k},\theta } \right)},\\ T=\sum\limits_{k=1}^N {{A_k}{r^{\lambda k - 1}}{T_k}\left({{\lambda _k},\theta } \right)}, \end{array}$ | (9) |
式中,r为距切口尖端的径向距离,Ak为幅值系数,λk为反映切口奇异性的奇性指数,N为截取的级数项数,${\tilde u}$rk(λk,θ),${\tilde u}$θk(λk,θ),${\tilde T}$k(λk,θ)为关于径向位移、周向位移以及温度的特征角函数.
取式(9)中的典型项,即Akrλk${\tilde u}$rk(λk,θ),Akrλk${\tilde u}$θk(λk,θ),Akrλk-1${\tilde T}$k(λk,θ)代入式(8),并将λk,${\tilde u}$rk(λk,θ),${\tilde u}$θk(λk,θ),${\tilde T}$k(λk,θ)简写为λ,${\tilde u}$r,${\tilde u}$θ,${\tilde T}$,有
| $\begin{align} & {{Q}_{33}}\tilde{u}_{r}^{''}+{{Q}_{32}}\tilde{u}_{\theta }^{''}+\left({{Q}_{32}}-{{Q}_{23}}+Q_{^{33}}^{'} \right)\tilde{u}_{r}^{'}+\left(Q_{^{32}}^{'}-{{Q}_{22}}-{{Q}_{33}} \right)\tilde{u}_{\theta }^{'}+\left(Q_{^{32}}^{'}-{{Q}_{22}} \right){{{\tilde{u}}}_{r}}+\\ & \left({{Q}_{23}}-Q_{^{33}}^{'} \right){{{\tilde{u}}}_{\theta }}+\left({{P}_{2}}-P_{3}^{'} \right)\tilde{T}-{{P}_{3}}{{{\tilde{T}}}^{'}}+\lambda \left({{Q}_{31}}+{{Q}_{13}} \right)\tilde{u}_{r}^{'}+\lambda \left({{Q}_{33}}+{{Q}_{12}} \right)\tilde{u}_{\theta }^{'}+\\ & \lambda \left(Q_{^{33}}^{'}-{{Q}_{13}}-{{Q}_{23}} \right){{{\tilde{u}}}_{\theta }}+\lambda \left({{Q}_{12}}-{{Q}_{21}}+Q_{^{31}}^{'} \right){{{\tilde{u}}}_{r}}+{{\lambda }^{2}}{{Q}_{11}}{{{\tilde{u}}}_{r}}+{{\lambda }^{2}}{{Q}_{13}}{{{\tilde{u}}}_{\theta }}-\lambda {{P}_{1}}\tilde{T}=0,\\ & {{Q}_{23}}\tilde{u}_{r}^{''}+{{Q}_{22}}\tilde{u}_{\theta }^{''}+\left({{Q}_{22}}+{{Q}_{33}}+Q_{^{23}}^{'} \right)\tilde{u}_{r}^{'}+\left({{Q}_{32}}-{{Q}_{23}}+Q_{22}^{'} \right)\tilde{u}_{\theta }^{'}+\left({{Q}_{32}}+Q_{22}^{'} \right){{{\tilde{u}}}_{r}}- \\ & \left({{Q}_{33}}+Q_{23}^{'} \right){{{\tilde{u}}}_{\theta }}-\left({{P}_{3}}+P_{2}^{'} \right)\tilde{T}-{{P}_{2}}{{{\tilde{T}}}^{'}}+\lambda \left({{Q}_{21}}+{{Q}_{33}}\right)\tilde{u}_{r}^{'}+\lambda \left({{Q}_{23}}+{{Q}_{32}} \right)\tilde{u}_{\theta }^{'}+\\ & \lambda \left(Q_{^{21}}^{'}+{{Q}_{32}}+{{Q}_{31}} \right){{{\tilde{u}}}_{r}}+\lambda Q_{31}^{'}{{{\tilde{u}}}_{\theta }}+{{\lambda }^{2}}{{Q}_{31}}{{{\tilde{u}}}_{r}}+{{\lambda }^{2}}{{Q}_{33}}{{{\tilde{u}}}_{\theta }}-\lambda {{P}_{3}}\tilde{T}=0,\\ & {{K}_{22}}{{{\tilde{T}}}^{''}}-\left({{K}_{12}}+{{K}_{21}}-K_{22}^{'} \right)+{{{\tilde{T}}}^{'}}+\left({{K}_{11}}-K_{21}^{'} \right)\tilde{T}-\lambda \left(2{{K}_{11}}-K_{21}^{'} \right)\tilde{T}+\\ & \lambda \left({{K}_{12}}+{{K}_{21}} \right){{{\tilde{T}}}^{'}}+{{\lambda }^{2}}{{K}_{11}}\tilde{T}=0,\\ \end{align}$ | (10) |
式中(…)″表示对坐标θ的二阶导数.式(10)中的λ2项导致微分方程组关于λ为非线性的,特引入如下代换变量
| $\begin{align} & {{{\tilde{g}}}_{r}}=\lambda {{{\tilde{u}}}_{r}},\\ & {{{\tilde{g}}}_{\theta }}=\lambda {{{\tilde{u}}}_{\theta }},\\ & {{{\tilde{g}}}_{T}}=\lambda \tilde{T}.\\ \end{align}$ | (11) |
将式(10)改写成如下的线性微分方程组
| $\begin{align} & {{Q}_{33}}\tilde{u}_{r}^{''}+{{Q}_{32}}\tilde{u}_{\theta }^{''}+\left({{Q}_{32}}-{{Q}_{23}}+Q_{^{33}}^{'} \right)\tilde{u}_{r}^{'}+\left(Q_{^{32}}^{'}-{{Q}_{22}}-{{Q}_{33}} \right)\tilde{u}_{\theta }^{'}+\left(Q_{^{32}}^{'}-{{Q}_{22}} \right){{{\tilde{u}}}_{r}}+\\ & \left({{Q}_{23}}-Q_{^{33}}^{'} \right){{{\tilde{u}}}_{\theta }}+\left({{P}_{2}}-P_{3}^{'} \right)\tilde{T}-{{P}_{3}}{{{\tilde{T}}}^{'}}+\lambda \left({{Q}_{31}}+{{Q}_{13}} \right)\tilde{u}_{r}^{'}+\lambda \left({{Q}_{33}}+{{Q}_{12}} \right)\tilde{u}_{\theta }^{'}+\\ & \lambda \left(Q_{^{33}}^{'}-{{Q}_{13}}-{{Q}_{23}} \right){{{\tilde{u}}}_{\theta }}+\lambda \left({{Q}_{12}}-{{Q}_{21}}+Q_{^{31}}^{'} \right){{{\tilde{u}}}_{r}}+{{\lambda }^{2}}{{Q}_{11}}{{{\tilde{g}}}_{r}}+{{\lambda }^{2}}{{Q}_{13}}{{{\tilde{g}}}_{\theta }}-\lambda {{P}_{1}}\tilde{T}=0,\\ & {{Q}_{23}}\tilde{u}_{r}^{''}+{{Q}_{22}}\tilde{u}_{\theta }^{''}+\left({{Q}_{22}}+{{Q}_{33}}+Q_{^{23}}^{'} \right)\tilde{u}_{r}^{'}+\left({{Q}_{32}}-{{Q}_{23}}+Q_{22}^{'} \right)\tilde{u}_{\theta }^{'}+\left({{Q}_{32}}+Q_{22}^{'} \right){{{\tilde{u}}}_{r}}- \\ & \left({{Q}_{33}}+Q_{23}^{'} \right){{{\tilde{u}}}_{\theta }}-\left({{P}_{3}}+P_{2}^{'} \right)\tilde{T}-{{P}_{2}}{{{\tilde{T}}}^{'}}+\lambda \left({{Q}_{21}}+{{Q}_{33}} \right)\tilde{u}_{r}^{'}+\lambda \left({{Q}_{23}}+{{Q}_{32}} \right)\tilde{u}_{\theta }^{'}+\\ & \lambda \left(Q_{^{21}}^{'}+{{Q}_{32}}+{{Q}_{31}} \right){{{\tilde{u}}}_{r}}+\lambda Q_{31}^{'}{{{\tilde{u}}}_{\theta }}+\lambda {{Q}_{31}}{{{\tilde{g}}}_{r}}+\lambda {{Q}_{33}}{{{\tilde{g}}}_{\theta }}-\lambda {{P}_{3}}\tilde{T}=0,\\ & {{K}_{22}}{{{\tilde{T}}}^{''}}-\left({{K}_{12}}+{{K}_{21}}-K_{22}^{'} \right)+{{{\tilde{T}}}^{'}}+\left({{K}_{11}}-K_{21}^{'} \right)\tilde{T}-\lambda \left(2{{K}_{11}}-K_{21}^{'} \right)\tilde{T}+\\ & \lambda \left({{K}_{12}}+{{K}_{21}} \right){{{\tilde{T}}}^{'}}+{{\lambda }^{2}}{{K}_{11}}{{{\tilde{g}}}_{T}}=0.\\ \end{align}$ | (12) |
假设切口径向边界上面力自由且绝热,这样的边界条件可以表达为
| $\begin{align} & {{\sigma }_{\theta }}=0,\\ & {{\tau }_{r\theta }}=0,\ \ \ \ \ \ \ \theta={{\theta }_{1}},{{\theta }_{2}}.\\ & {{h}_{\theta }}=0,\\ \end{align}$ | (13) |
将式(9)的典型项代入式(4)和(6)中σθ,τrθ,hθ的表达式,边界条件式(13)可重新写为
| $\begin{align} & {{Q}_{23}}\tilde{u}_{r}^{'}+{{Q}_{22}}\tilde{u}_{\theta }^{'}+{{Q}_{22}}\tilde{u}_{r}^{'}-{{Q}_{23}}{{{\tilde{u}}}_{\theta }}-{{P}_{2}}\tilde{T}+\lambda {{Q}_{21}}{{{\tilde{u}}}_{r}}+\lambda {{Q}_{23}}{{{\tilde{u}}}_{\theta }}=0,\\ & {{Q}_{33}}\tilde{u}_{r}^{'}+{{Q}_{32}}\tilde{u}_{\theta }^{'}+{{Q}_{32}}\tilde{u}_{r}^{'}-{{Q}_{33}}{{{\tilde{u}}}_{\theta }}-{{P}_{3}}\tilde{T}+\lambda {{Q}_{31}}{{{\tilde{u}}}_{r}}+\lambda {{Q}_{33}}{{{\tilde{u}}}_{\theta }}=0,\ \ \ \ \ \ \ \theta={{\theta }_{1}},{{\theta }_{2}},\\ & {{K}_{22}}{{{\tilde{T}}}^{'}}-{{K}_{21}}\tilde{T}+\lambda {{K}_{21}}\tilde{T}=0.\\ \end{align}$ | (14) |
至此,正交各向异性切口热弹奇性指数的计算转化为在边界条件式(14)下方程组式(11)、(12)的特征值求解问题.运用插值矩阵法[12]可以成功求解该类特征值问题,获取切口尖端的奇性指数λ和相应的特征角函数${\tilde u}$r,${\tilde u}$θ,${\tilde T}$.
2 数值算例考虑如图 1所示的正交各向异性平面V形切口,材料参数按表 1所列的A、B、C三种情况给出,情形A和B区别在于材料的柔度系数不同,情形B和C仅材料的铺设角度不同.通过插值矩阵法求解在边界条件(14)下的方程组(11)、(12),可以一次性地获得若干阶特征值(奇性指数),考虑到在(0,1)区间内,方程组特征值对应应力和热流奇异项,其在物理场渐近展开式中占主导作用,以下仅列出了在(0,1)区间内的奇性指数.
| 表1 三种材料铺设角φ/°、柔度系数sij/(10-11m2N-1)、导热系数kii/(102WK-1m-1)和热膨胀系数αi/(10-5K-1) Table 1 Plying angle φ/°, flexibility coefficient sij/(10-11m2N-1), thermal conductivity coefficient (kii/(102WK-1m-1) and thermal expansion coefficient (αi/(10-5K-1) in three cases |
 |
| 点击放大 |
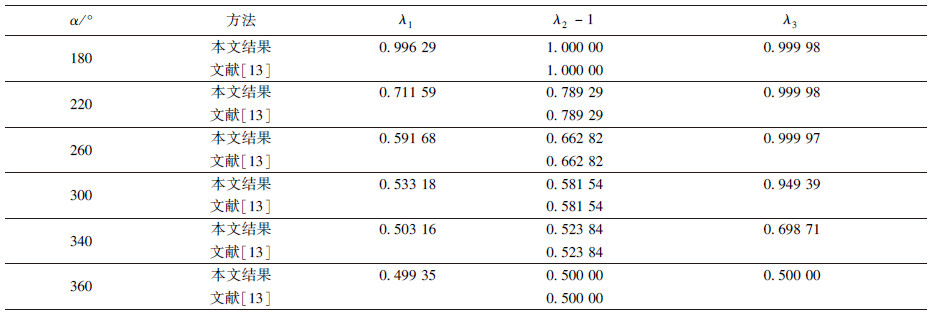
表 2所列为情形A时切口的热弹奇性指数,从中可以看出切口张角α>180°才发生奇异性,而且存在三个奇性指数.文献[13]通过渐近展开法和边界元法结合分析了切口尖端的热流奇异性,将文[13]结果列于表 2以作比较.从中可以看出,本文计算得到的奇性指数λ2能与文[13]计算结果吻合一致,从而说明,λ2为热流奇性指数,λ1、 λ3则应为应力奇性指数.为了进一步说明,我们选取切口张角α=300°时所计算得到的特征角函数绘于图 2.从图 2中可以看出,λ1、 λ3对应的特征角函数仅有${\tilde u}$r和${\tilde u}$θ,而λ2对应的特征角函数仅有${\tilde T}$,这也说明了λ1、 λ3为应力奇性指数而λ2为热流奇性指数.另外,从表 2中还可以看出,文[13]仅能获取热流奇性指数,而没办法计算出应力奇性指数.
| 表2 切口热弹奇性指数(情形A) Table 2 Thermo-elastic singular orders of orthotropic materialV-notch (Case A) |
 |
| 点击放大 |
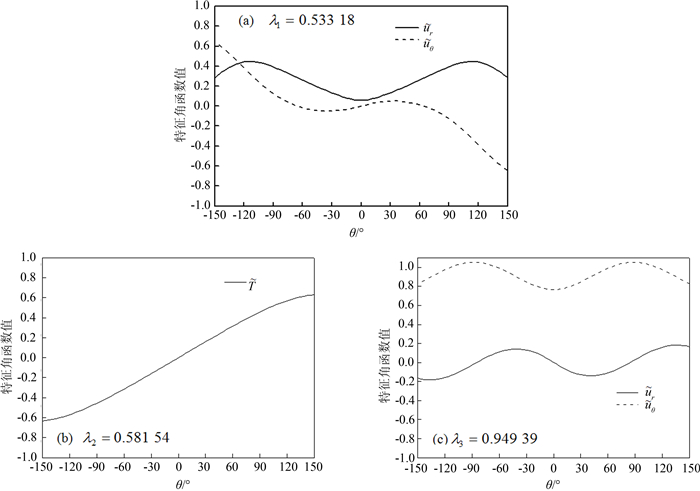 |
| 图2 切口开角为300°时的特征角函数(情形A)< Fig. 2 Characteristic angular functions for a V-notch in Case A as α=300° |
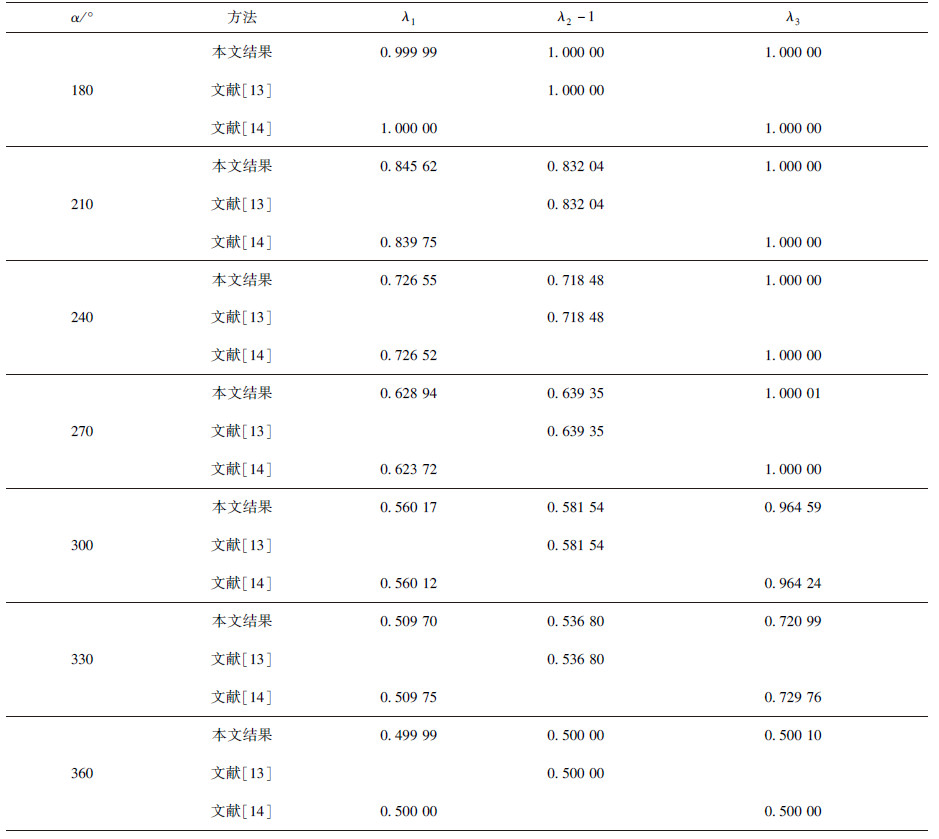
材料参数为情形B和C时,切口的奇性指数计算结果分别列于表 3和表 4,此时也仅有三个奇性指数,奇异性随着切口张角的增大而变强,切口张角为360°(也就是裂纹)时切口奇异性最强,三个奇性指数均为0.5.对比表 3和表 4发现,当切口张角相同时,材料铺设角度φ=0°切口的热流奇异性比材料铺设角度φ=90°时强,而应力奇异性却比它弱.
| 表3 切口热弹奇性指数(情形B) Table 3 Thermo-elastic singular orders of orthotropicmaterial V-notch (Case B) |
 |
| 点击放大 |
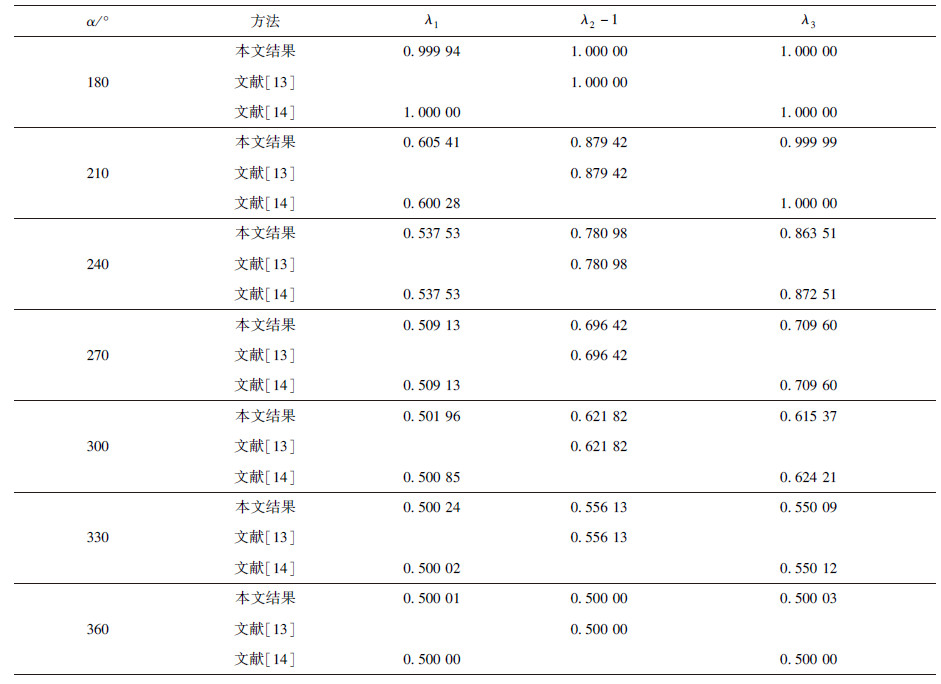
| 表4 切口热弹奇性指数(情形C) Table 4 Thermo-elastic singular orders of orthotropicmaterial V-notch (Case C) |
 |
| 点击放大 |
文献[13]分析了切口尖端的热流奇异性,文献[14]则分析了切口尖端的应力奇异性,现将他们的分析结果作为对照一并附上.通过比较可以看出,本文方法可以同时获取应力和热流奇性指数,且与文献结果误差非常小,而文[13]和文[14]是分别从热流和应力奇异性两个侧方面来考虑.因而,本文方法适用性更加广泛.
3 结论提出计算正交各向异性材料切口热弹奇性指数的方法.通过引入切口尖端热弹物理场的渐近展开式,将求解切口奇性指数问题转化为常微分方程组的特征值问题,并用插值矩阵法求解,可以同时获取切口关于应力、热流的奇性指数和特征角函数.对多种不同材料参数组合进行了计算,算例显示所提方法适用于任意张角的V形切口,也不受限于材料的铺设角,能够一次性分析应力奇异性和热流奇异性指数,适应性强.本文计算结果与相应文献结果很好吻合,计算精度高.
| [1] | FU X R, LONG Y Q. Analysis of plane notch problems with analytical trial functions' method[J]. Engineering Mechanics, 2003, 20(4):33-38. |
| [2] | XU J Q, MUTOH Y. Analytical solution for interface stresses due to concentrated surface force[J]. International Journal of Mechanical Sciences, 2003, 45:1877-1892. |
| [3] | ZHANG M, YAO Z H, DU Q H. Boundary element analysis of stress intensity factors of bimaterial interface crack[J]. Chinese Journal of Applied Mechanics,1999, 16(4):21-26. |
| [4] | ZHENG B L, DAI Y, JI X, et al. The stress singularity analysis of an antiplane problem near the interface end[J]. Chinese Journal of Applied Mechanics, 1999,4:21-26,164. |
| [5] | GE R Y, NIU Z R, CHENG C Z, et al. Propagation analysis of two-dimensional linear elastic crack with boundary element method[J]. Chinese Journal of Computational Physics, 2015, 32(3):310-320. |
| [6] | CHENG C Z, GE R Y, XUE W W, et al. Singularity at tip of a composite notch under anti-plane loading[J]. Chinese Journal of Computational Physics, 2013, 30(5):700-705. |
| [7] | PRASAD N N V, ALIABADI M H, ROOKE D P. Effect of thermal singularities on stress intensity factors:edge crack in rectangular and circular plate[J]. Theoretical and Applied Fracture Mechanics, 1996, 24:203-215. |
| [8] | CAICEDO J, PORTELA A. Cracked plate analysis with the dual boundary element method and Williams' eigenexpansion[J]. Engineering Analysis with Boundary Elements, 2015, 52:16-23. |
| [9] | YOSIBASH Z, SZABO B A. Numerical analysis of singularities in two-dimensions Part 1:computation of eigenpairs[J]. International Journal for Numerical Methods in Engineering, 1995, 38:2055-2082. |
| [10] | PING X C, XU X X, CHENG M C. Singular stress analysis of an irregular shaped inclusion under thermo-mechanical loads[J]. Chinese Journal of Computational Mechanics, 2014, 6:749-754. |
| [11] | AYATOLLASHI M R, MIRSAYAR M M, DEHGHANY M. Experimental determination of stress field parameters in bi-material notches using photoelasticity[J]. Materials and Design, 2011, 32:4901-4908. |
| [12] | NIU Z R, GE D L, CHENG C Z, et al. Evaluation of the stress singularities of plane V-notches in bonded dissimilar materials[J]. Applied Mathematical Modelling, 2009, 33, 1776-1792. |
| [13] | CHENG C Z, HAN Z L, YAO S L, et al. Analysis of heat flux singularity at 2D notch tip by singularity analysis method combined with boundary element technique[J]. Engineering Analysis with Boundary Elements, 2014, 46:1-9. |
| [14] | MANTIC V, PARIS F, CANAS J. Stress singularities in 2D orthotropic corners[J]. International Journal of Fracture, 1997, 83:67-90. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
