| 管流中注入粒子的非定常波系的数值研究 |
存在大量细小悬浮固体颗粒的空气通常被称为含灰气体.在含灰气体中,气体的流动状态和粒子的分布与动力学特性会被粒子与气体的相互作用所改变.自然现象中,如彗星核向其周围大气的蒸发,工程应用中的航天工程欠膨胀喷管射流与迎面高超声速气流的相互作用,还有高新技术应用中采用对撞射流喷雾器干燥颗粒材料等方面,建立这类效应的数值模型有着重要的研究意义.
1962年Saffman发现在低Stokes数下粒子对黏性流体有着极其快速的响应[1],并指出随着粒子数密度的增加,含灰流体的临界雷诺数变小,这使粒子对扰动的响应时间变短,导致流体流动不稳定.随后,人们对含灰气体流动进行了多方面研究,其中上个世纪50年代的含尘气体方程是两相流连续介质模型发展的里程碑,这些模型由Marble(1970)加以总结.后期的研究如超声速含灰气体钝体绕流[2]、超声速气流中含灰气体点源流动[3]、含灰气体在变截面管道中的流动[4]、存在激波的含灰气体流动[5]等.
对含灰气体流动的研究多采用两相流模型,从理论研究刻画的尺度和所建立的控制体属性来划分,主要可分为三大类物理模型,即连续介质模型、离散颗粒模型、流体拟颗粒模型[6].连续介质模型把宏观上离散的颗粒拟为流体相,这些拟成的流体相的颗粒与流体在同一时间充满同一空间,两相方程的形式统一,便于研究比较[7].这种模型发展相对成熟和完善,是目前多相流研究中应用最广泛的理论模型.但是,不能用于模拟计算存在相变的流场和其基本方程组的封闭问题是它的缺点.离散颗粒模型则对单个固体颗粒及其碰撞行为进行跟踪研究[8],反映了气固两相流的实际运动机理,所得到的颗粒方程为常微分方程,易于求解.但是,颗粒轨道模型的缺点是由于粒子数量众多,数值计算会花费大量的计算时间.流体拟颗粒模型是一个从微观尺度上研究多相流的物理模型[9],不但把固体颗粒作为离散相来处理,而且把流体也离散成固体颗粒尺度上“拟颗粒”来处理.它的缺点在于需要比离散颗粒模型更加庞大的计算时间.
1996年Crowe及其合作者[10]综述了各种稀相气固两相流的数值计算方法,它们大体上可划分为Euler方法和Lagrange方法两类.众所周知,Euler/Euler数值模拟法和Euler/Lagrange数值模拟法两者各有优点和缺点.特别是用E/L数值模拟法可以获得不同尺寸的颗粒离散相的颗粒轨迹等具体信息[11],只不过就目前的计算技术而言,由于计算时间无限长而无法应用于真实的高浓度气固两相流动[12].对于E/E数值模拟法具有在计算上易于求解和在物理方面易于理解的优点,但是,它的缺点是不适合于计算具有不同颗粒特征(如不同颗粒尺寸、密度等)和存在相变的气固两相流动.关于含灰气体流动近期Jacobs等人发展了一套基于WENO的算法[13]和Euler-Lagrange模式的算法[14],来模拟高速含灰气流问题.
在所有含灰气体的研究中,关于可压缩流动的研究很有必要.在可压缩含灰气体流动中,固体颗粒对流场的影响可模型化为可压缩流场的添质、加热效应.对于可压缩流动中的一维加热理论迄今为止的研究也有很多.现有的气体动力学教科书通常会包括一维管道的理想均匀加热理论.对于加热引起的波系研究,Bartlm首先针对不同状态下的一维加热结果进行了分类[15].后来,这一分析也被Delale 等先后扩展至准一维喷管流[16]及二维超声速膨胀流[17].近年来的综述广泛讨论了这方面的内容[18, 19].然而,上述提及的文献中研究主要对象是稳定的流场,而关于粒子注入过程中产生的非定常波,则少有涉及.2002年van Dongen 初次针对不同来流条件下加热产生的非定常波进行了预测[20].
同样,可压缩流动中的质量交换问题也受到了广泛的关注[21].在以往的研究中主要的研究对象是从火箭燃料助推器中提出的模型问题,其中经常需要假设注入过程沿一维管壁作用.沿管壁可以选取控制体建立质量、动量、能量的守恒关系式.然而本文关注的一维管道中固定位置处注入粒子中,质量交换过程是沿着时间方向不断进行,且交换区域很小.在这种情况下,若来流参数未被扰动,则质量交换过程可以直接通过积分方式来描述.
基于上述可压缩流动中的热质交换问题,现有对于含灰气体流动的研究,大多关注来流条件改变后粒子与气流间的弛豫作用,而关于流场热质交换的产生波系结构变化的研究较少.吴清松[22]考察了激波引导二维喷管流的各种波系结构,对于在含灰气体中产生的波系做出了独特的分析.罗喜胜[23]研究了在喷管喉道下游注入粒子的物理过程,分析了在不同物理条件下,流场和粒子之间的力和热的相互作用.
在可压缩流动中,注入固体粒子时,由于添质的堵塞作用,会使流场的压力产生变化,从而在流场中会产生一系列波系结构.同时,对流场加热也会使流场中的波系结构产生变化.本文研究添质和加热过程中引起的非定常波系,讨论两者相互作用导致的波系间转换,最后求解流场中各区域的热力学参数,分析各非定常波的波强.
1 物理模型和数值方法通常假设含灰气体粒子间不发生碰撞,忽略粒子体积和重力作用,假设粒子是外形为圆形、大小一致、粒子比热是常数、温度分布均匀的颗粒,气相为量热完全气体,只考虑气固两相作用时的黏性和热传导作用.本文使用连续介质模型,流场的守恒型控制方程可写为
| $\frac{{\partial \boldsymbol{U}}}{{\partial t}} + \frac{{\partial \boldsymbol{F}}}{{\partial x}} + \frac{{\partial \boldsymbol{G}}}{{\partial y}} = \boldsymbol{S},$ | (1) |
采用分裂步算法对控制方程中流体流动部分和源项部分进行分别处理,其中流体流动控制方程使用基于非结构四边形网格的中心型有限体积方法进行离散,并采用MUSCL-Hancock格式进行求解从而达到空间、时间二阶的求解精度[24].源项的处理则采取二阶时间积分方法.
考虑不同来流情况下注入粒子对流场的影响.图 1是计算域的示意图,图中q代表注入粒子的质量,M1代表来流马赫数.计算域是100 cm×0.3 cm长方形,气流沿x轴正向流动,-50 cm≤x≤50 cm,y轴左右两端为开口边界条件,中间为固壁边界条件,网格大小是0.1 cm×0.1 cm.在算法上通过每个计算时间步对位置-0.2 cm≤x≤0.2 cm施加当地高数密度的粒子参数条件,来实现在该处往稳定流场中持续注入速度为0的固体粒子,使填入质量比κ=0.5.来流温度为293 K,压强为101 300 Pa的氮气.粒子直径5 μm,材质是铜,密度8 960 kg·m-3.
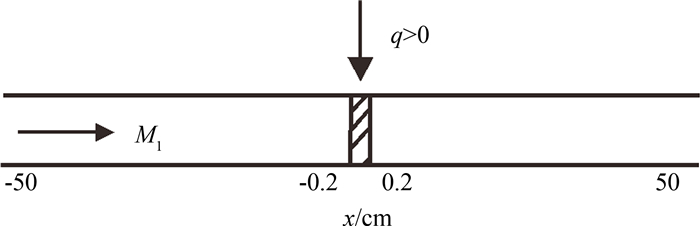 |
| 图1 计算域示意图 Fig. 1 Computational domain |
控制来流马赫数为0.6,同时控制注入粒子温度,加入质量初始滞止焓值hp0与气流初始滞止焓值h0相等,此时的流场只存在添质效应.图 2为hp0=h0时,亚声速条件下粒子数密度g和流场压强P的x-t分布图.注入粒子对亚声速流场形成“堵塞”,于x=0处分别产生一簇上行压缩波Su和下行稀疏波EF,EF之后存在一簇稀疏波Ed,并且在波系EF和Ed之间存在一处接触间断CD.从图 2中可以看出添质引起的波系变化和粒子随气体流动不断加速的过程.图 3是0.6 ms时流场压强P、温度T、粒子密度g的沿x轴向分布图.其中P=400Pφ+PC,T=0.4Tφ+TC,g=10gφ,PC=99 635 Pa,TC=292.7 K.可以发现,在粒子分布区域下游,温度有一峰值区域,这一接触间断是由于粒子与气流间动量和能量传递造成的.压强和温度分布中均可清晰观察到上行压缩波Su,稀疏波EF,接触间断CD和下行稀疏波Ed.文献[20]详细阐述了非定常流动不同流速下添质效应产生波系的机理和现象预测,结果与其吻合.
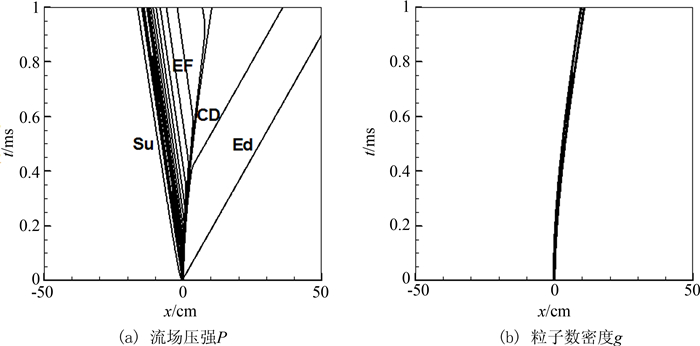 |
| 图2 亚声速流场添质流的x-t分布 Fig. 2 x-t distribution within 1ms in subsonic condition as hp0=h0 |
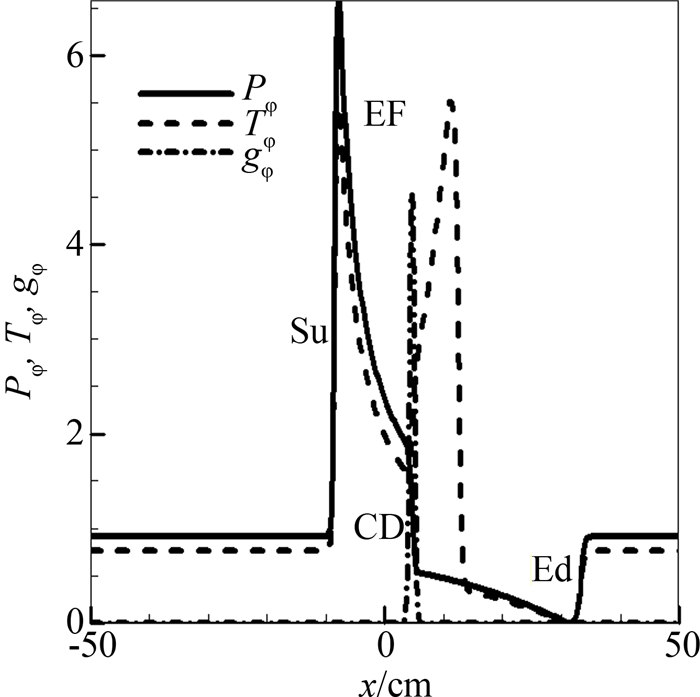 |
| 图3 0.6 ms时亚声速流场添质流流场压强P、温度T、粒子密度g沿x轴向分布 Fig. 3 Gas pressure P, gas temperature T and particle density g distributions along x-axis in subsonic condition at 0.6 ms |
这时增大注入粒子的温度,在考虑流场添质效应的同时,考虑流场的加热效应.图 4为Tp=1.05T(hp0=h0)、2T、4T三种情况下1 ms内的流场压强x-t波系分布.图 5(a)为0.6 ms时Tp=0.5T,1.05T(hp0=h0),2T,3T,4T五种情况下的流场压强的沿x轴向分布.从图中可以得出,对于亚声速流场,加热会使流场内气体产生膨胀,这时加热效应与添质效应对流场的影响逐渐抵消,流场下游压强逐渐增大,上行压缩波Su和下行稀疏波EF逐渐增强,下行稀疏波Ed逐渐减弱直至下行稀疏波转化为压缩波.当Tp=2T时,如图 4(b)所示,向下游传播的稀疏波系已非常弱,基本可以忽略.继续增大注入粒子温度,加热效应的影响继续增大,转化后的压缩波逐渐增强.文献[20]同时详细阐述了非定常流动不同流速下加热效应产生波系的机理和现象预测,可以发现加热流下游波系会对流场产生与添质流相反的影响,本文结果与文献吻合.图 5(b)是0.6 ms时在以上5种情况的粒子速度沿X轴向分布,可以发现,改变注入粒子温度对流场中粒子的速度有4%的影响.
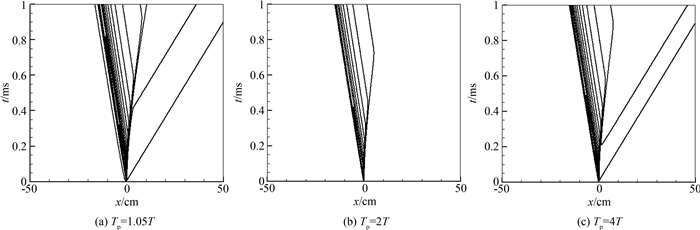 |
| 图4 不同初始注入粒子温度下亚声速流场压强P的x-t分布 Fig. 4 Gas pressure x-t distributions within 1ms in subsonic condition at different initial particle temperature |
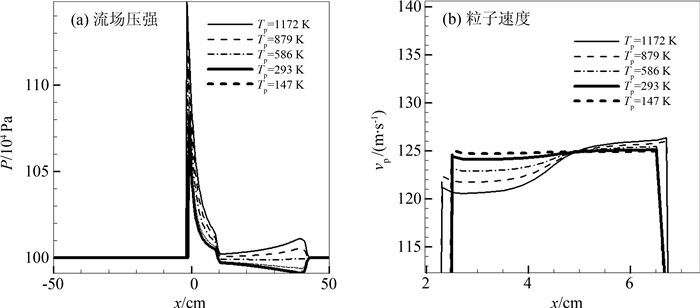 |
| 图5 ms时亚声速流场Tp=0.5T,1.05T,2T,3T,4T情况的沿x轴向分布 Fig. 5 Distributions along x-axis in subsonic condition at 0.6 ms as Tp=0.5T, 1.05T, 2T, 3T and 4T |
只考虑添质作用,在跨声速流场和超声速流场的波系与亚声速有所不同.图 6(a)是来流马赫数1.5时流场压强的x-t分布.图 6(b)是来流马赫数1的流场压强x-t分布,结合图 2(a)、图 6(a)、图 6(b),可以发现非定常波系随来流速度的变化过程.增大来流流速,波系整体向下游偏移.就波系结构而言,来流不同并未带来显著变化,向上游和下游传播的波系仍均为压缩波及伴随其后的稀疏波.而图 7为Tp=1T、3T、5T三种情况下0.45 ms时的流场压强沿x轴向分布图.可以发现,下行波系的波强远小于上行压缩波.同时,随着加入粒子的温度增大,下传波系的变化趋势与亚声速来流情况下结果一致.图 8是0.6 ms时不同马赫数流场的粒子温度的沿x轴向分布,可以发现,改变来流马赫数对流场中粒子的温度会有1.6%的影响.
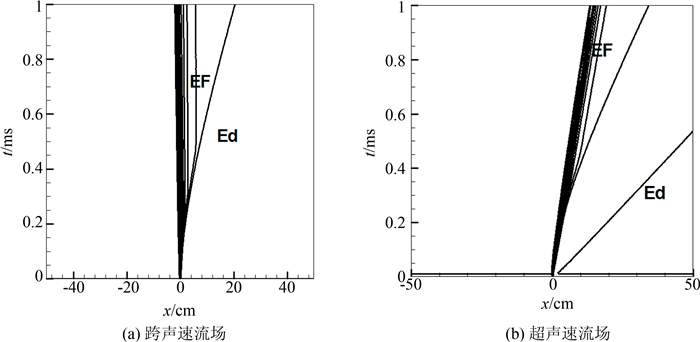 |
| 图6 不同马赫数流场添质流压强P的x-t分布 Fig. 6 Gas pressure x-t distributions within 1 ms with different Mach number gas flow as hp0=h0 |
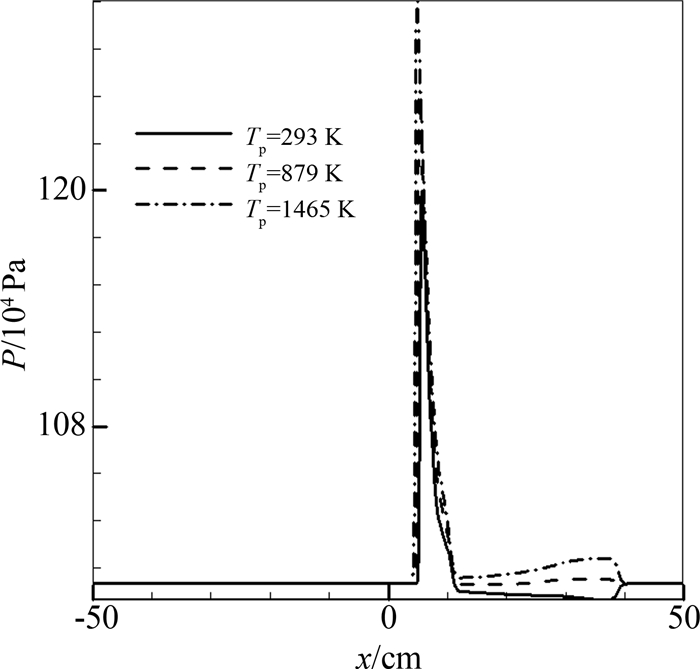 |
| 图7 0.45 ms时超声速流场Tp=1.05T、3T、5T的流场压强P沿x轴向分布 Fig. 7 Gas pressure distributions along x-axis at 0.45 ms in supersonic condition as Tp=1.05T, 3T and 5T |
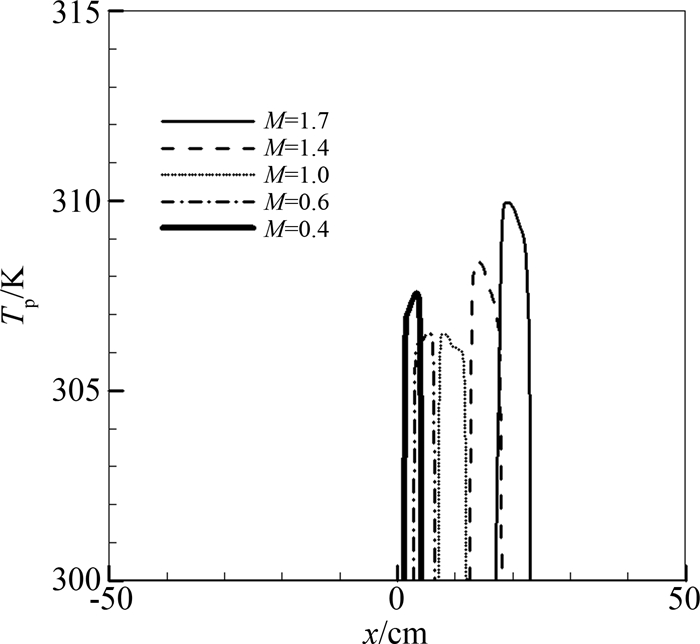 |
| 图8 0.6 ms时不同马赫数流场的粒子温度Tp沿x轴向分布 Fig. 8 Particle temperature distributions along x-axis at 0.6 ms as Ma=0.6, 1.0, 1.4 and 1.7 at hp0=h0 |
图 9(a)、(b)、(c)分别为来流亚声速、跨声速和超声速下流场固定时刻流场压强沿x轴向分布示意图.上行压缩波Su的波强是(p2-p1)/p1,稀疏波EF的波强为(p4-p3)/p3,下行稀疏波Ed的波强是(p5-p6)/p6.图 10是0.45 ms时在不同的流场速度和粒子温度情况下各个非定常波波强的相图.从中可以发现,上行压缩波Su和稀疏波EF的波强远大于下行稀疏波Ed,增大来流马赫数和初始粒子温度均会增大Su波系和EF波系的强度.在相同来流马赫数下,随着注入粒子的温度升高,Ed波的波强先是减小,直至波系结构改变,稀疏波转化为压缩波.其后压缩波的波强又会逐渐增大.另一方面,对于相同的注入粒子温度,增大来流速度,当注入粒子的焓值高于流场焓值时,在稀疏波EF的波后还会存在一道压缩波向下游传播,随着来流速度的增大,压缩波的波强会逐渐减弱,但波系结构不会变化.如果注入粒子焓值低于流场焓值,在稀疏波EF的波后会存在一道稀疏波向下游传播,随着来流速度的增大,稀疏波的波强反而会增大.
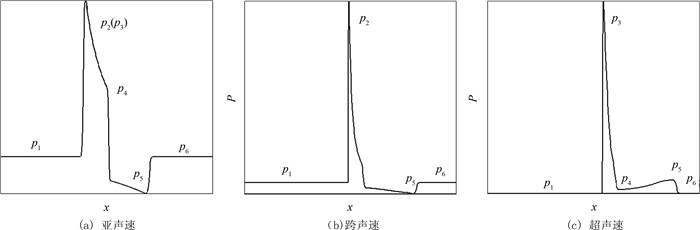 |
| 图9 不同马赫数下流场固定时刻流场压强沿x轴向分布示意图 Fig. 9 Gas pressure theoretical distributions along x-axis at fixed time with different flow Mach numbers |
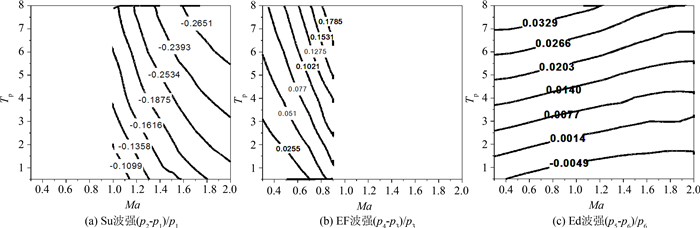 |
| 图10 不同来流马赫数和粒子温度下3种波的波强分布相图 Fig. 10 Phase diagrams of different wave strength at 0.45 ms with different initial particle temperatures and flow Mach numbers (Numbers in particle temperature represent multiple of flow temperatures.) |
采用有限体积方法对可压缩流场粒子注入的过程进行数值研究.着重发展并验证加热过程引起的非定常波系,讨论波系间的转换,最后求解流场中各区域的热力学参数,分析各非定常波的波强.结果表明:
1) 改变流场的马赫数和初始注入粒子温度影响流场产生的波系结构.对于亚声速流场,当注入粒子的焓值与流场一致时,会产生一道压缩波和一道稀疏波分别向流场上下游传播,同时在下行稀疏波波后会产生一道稀疏波向下游传播.如果增大初始粒子温度,加热效应与添质效应共同作用于流场,随着加热效应的增大,下行稀疏波会逐渐减弱直至改变波系结构,产生新的压缩波.另一方面,不改变注入粒子的温度,只增大来流速度,只会使波系整体向下游偏移,波系结构不会发生改变.
2) 流场马赫数和初始注入粒子温度影响流场产生的波系强度.增大来流马赫数和初始粒子温度均会增大Su波系和EF波系的强度.对于相同的来流速度,如果注入粒子焓值低于流场焓值时,在下行稀疏波的波后会存在一道稀疏波向下游传播,这时增大初始粒子温度会使下行稀疏波的波强会逐渐减小,直至波系结构改变,稀疏波转化为压缩波.其后压缩波的波强又会逐渐增大.
3) 当注入粒子的焓值高于流场焓值时,在下行稀疏波的波后还会存在一道压缩波向下游传播,随着来流速度的增大,压缩波的波强减弱,但波系结构不会变化;如果注入粒子焓值低于流场焓值时,在下行稀疏波的波后会存在一道稀疏波向下游传播,随着来流速度的增大,稀疏波的波强反而会增大.
关于流场对粒子参数的影响和作用,本文仅给出了一些现象的描述.通过理论和数值上对粒子参数发生变化的精确预测,是下一步需要开展的工作.
| [1] | SAFFMAN P G. On the stability of laminar flow of a dusty gas[J]. Journal of Fluid Mechanics, 1962, 13(1):120-128. |
| [2] | Sakharov, 王柏懿. 超声速含灰气体钝体绕流的传热增强及颗粒惯性沉积效应[J]. 自然科学进展, 2002, 12:3. |
| [3] | 王柏懿, 欧西普措夫A N, 特维若夫斯基M A. 超声速气流中含灰气体点源流动特性[J]. 应用数学和力学, 2003, 24(8):821-826. |
| [4] | 王柏懿, 吴清松. 变截面管道中激波诱导的两相流动[J]. 空气动力学学报,1992, 10(3):355-361. |
| [5] | BOIKO V M, KISELEV V P, KISELEV S P, et al. Shock wave interaction with a cloud of particles[J]. Shock Waves, 1997, 7(5):275-285. |
| [6] | 马银亮. 高浓度气固两相流的数值模拟研究[D]. 杭州:浙江大学博士学位论文, 2001:17-26. |
| [7] | HORIO M, IWADATE Y, SUGAYA T. Particle normal stress distribution around a rising bubble in a fluidized bed[J]. Powder Technology, 1998, 96(2):148-157. |
| [8] | TSUJI Y, TANAKA T, YONEMURA S. Cluster patterns in circulating fluidized beds predicted by numerical simulation (discrete particle model versus two-fluid model)[J]. Powder Technology, 1998, 95(3):254-264. |
| [9] | GE W, LI J. In cireulating fluidized bed technology[M]. KWAUK M,LI J, ed.Beijing:Science Press,1996:0-266. |
| [10] | CROWE C T, TROUTT T R, CHUNG J N. Numerical models for two-phase turbulent flows[J]. Annual Review of Fluid Mechanics, 1996, 28(1):11-43. |
| [11] | LOEKWOOD F C, PPADAOPOULOS C, ABBAS A S. Prediction of a comer-fired power station combustor[J].Combustion Science and Technology, 1988, 58(1-3):5-23. |
| [12] | ANDREWS M J, ROURKE P J O. The multi phase particle-in-cell(MP-PIC) method for dense particulate flow[J].Int J Multiphase Flow,1996,22:379-402. |
| [13] | JACOBS G B, DON W S. A high-order WENO-Z finite difference based particle-source-in-cell method for computation of particle-laden flows with shocks[J]. J Comput Phys, 2009,228:1364-1379. |
| [14] | SENATORE G, DAVIS S, JACOBS G. The effect of non-uniform mass loading on the linear, temporal development of particle-laden shear layers[J]. Physics of Fluids, 2015, 27(3):033302. |
| [15] | BARTLMÄ F. Instationäre strömungsvorgänge bei uberschreiten der kritischen wärmezufuhr[J]. Z Flugwiss, 1963,11:160-168. |
| [16] | DELALE C F, SCHNERR G H, ZIEREP J. The mathematical theory of thermal choking in nozzle flow[J]. Zeitschrift für Angewandte Mathematik und Physik, 1993,44:943-976. |
| [17] | DELALE C F,VAN DONGEN M E H. Thermal choking in two-dimensional expansion flows[J]. Zeitschrift Fürangewandte Mathematik und Physik, 1998,49:515-537. |
| [18] | SCHNERR G H. Unsteadiness in condensing flow:dynamics of internal flows with phase transition and application to turbomachinery[C]//Proc-IMechE Part C:J. Mechanical Engineering Science, 2005,219:1369-1410. |
| [19] | DELALE C F, SCHNERR G H, VAN DONGEN M E H. Shock wave scienceand technology reference library[M]//Condensation discontinuities and condensation induced shockwaves. Berlin:Springer, 2007:188-230. |
| [20] | VAN DONGEN M E H, LUO X, LAMANNA G, et al. On condensation induced shock waves[C]//Proceedings of the 10th Chin Symp Shock Waves, 2002:1-11. |
| [21] | SHAPIRO A H. The dynamics and thermodynamics of compressible fluid flow[M]. 1st. The Ronald Press Company, 1953. |
| [22] | WU Q S, WANG D Z, XU Y H, et al. Wave pattern characteristics of a two-phase nozzle flow by shock propagation[J]. Shock Waves, 1997,7:127-133. |
| [23] | LUO X, WANG G, OLIVIER H. Parametric investigation of particle acceleration in high enthalpy conical nozzle flows for coating applications[J]. Shock Waves, 2008, 17(5):351-362. |
| [24] | SUN M, TAKAYAMA K. Conservative smoothing on an adptive quadrilateral grid[J]. J Comput Phys, 1999, 150:143-180. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
