| 相场法模拟第二相颗粒对柱状晶形成的影响 |
2. 广西高校复杂系统优化与大数据处理重点实验室, 玉林师范学院 物理科学与工程技术学院, 玉林 537000
2. Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Large Data Processing, College of Physics Science and Engineering, Yulin Normal University, Yulin 537000, China
Grain size and uniformity are key factors that influence mechanical properties of polycrystalline materials[1]. One effective way to improve material performance is to control grain growth with heat treatment technology. Although in most cases grain refinement is beneficial to mechanical properties of polycrystalline materials,it is not always the case,especially for high temperature materials that require coarse grains to enhance high temperature strength and creep resistance[2, 3]. Controlling the evolution of grain structure is crucial to the optimization of materials properties through processing[4]. Recently,directional annealing has been successfully applied in the experiment to produce columnar grain structures for several metallic materials[5, 6]. Columnar grain structures can improve fatigue resistance,enhance creep property and impart crack-stopping behavior[7, 8]. Therefore,it is significant to study the growth process of columnar grain under directional annealing.
In recent years,several modeling techniques have been successfully applied to study grain growth during directional annealing,including Monte Carlo Potts,front-tracking and phase field. Holm et al[9] used Monte Carlo method (Potts model) to simulate non-uniform grain growth,and analyzed grain growth kinetics during directional annealing. Badmos et al[10, 11] used the front-tracking method to simulate the growth process of columnar grain and discussed the effect of variable boundary energy and mobility on the evolution of columnar grain in single-phase polycrystalline materials during directional annealing. By setting the grain boundary mobility as a Gaussian function,Wei and Li[12] investigated the grain growth behavior under the influence of temperature gradient using the phase field method. Ohno et al[13] studied the discontinuous grain growth leading to a coarse columnar austenite grain structure in as-cast peritectic carbon steels in two- and three-dimensional (2D&3D) multi-phase field models. The experimental study in Ref. [14] revealed that SPPs (i.e.,oxide particles) have a significant influence on columnar grain growth,whereas the above simulated studies did not take into consideration. Therefore,a good understanding of the effect of SPPs on columnar grain growth is essential.
The phase field method[15, 16] has emerged as a versatile tool for simulating microstructure evolution phenomena,such as solidification[17],recrystallization[18],grain growth[19] and crack propagation[20, 21]. In our previous studies[22, 23],a phase field model with a moving hot zone under directional annealing has been developed,which is used to study the effect of hot zone width on the formation and continuous propagation of columnar grain structure without SPPs during directional annealing. The objective of this study is to study the effect of SPPs on columnar grain growth in polycrystalline materials during directional annealing.
1 Phase field model with a moving hot zone 1.1 Phase field model for grain growth with SPPsIn the phase field model[15, 16] for grain growth of single-phase polycrystalline materials,the microstructure of polycrystalline materials is described by a set of continuous variables,η1(r,t),η2(r,t),…,ηP(r,t),where P is the total number of possible orientations in space and ηi(i=1,2,…,P) are called orientation field variables which distinguish different orientations of grains and are continuous in space,r is the spatial coordinate and t is the time. According to Moelans et al[24],a spatially dependent function φ(r) that equals 1 inside SPPs and 0 in the matrix grains is used to describe the distribution of SPPs,which is considered constant in time.
Total free energy of the system containing SPPs is described by[24]
| $ F=\int{_{V}\left\{ \sum\limits_{i=1}^{P}{\left( -\frac{a}{2}\eta _{i}^{2}+\frac{\beta }{4}\eta _{i}^{4} \right)+\gamma \sum\limits_{i=1}^{P}{\sum\limits_{j\ne i}^{P}{\eta _{i}^{2}\eta _{j}^{2}+\phi }}}\sum\limits_{i=1}^{P}{\eta _{i}^{2}+}\sum\limits_{i=1}^{P}{\frac{{{k}_{i}}}{2}{{\left( \nabla {{\eta }_{i}} \right)}^{2}}} \right\}{{\text{d}}^{3}}r}, $ | (1) |
The spatial and temporal evolution of orientation field variables are described by the time-dependent Ginzburg-Landau equations for non-conserved order parameters[24]
| $ \frac{\partial {{\eta }_{i}}\left( r,t \right)}{\partial t}=-{{M}_{i}}\frac{\delta F}{\delta {{\eta }_{i}}\left( r,t \right)}=-{{M}_{i}}\left[ \left( 2\phi -a \right){{\eta }_{i}}+\beta \eta _{i}^{3}+2\gamma {{\eta }_{i}}\sum\limits_{j\ne i}^{P}{\eta _{i}^{2}-{{k}_{i}}{{\nabla }^{2}}{{\eta }_{i}}} \right],i=1,2,\cdots P, $ | (2) |
| $ {{\nabla }^{2}}{{\eta }_{i}}=\frac{1}{{{\left( \vartriangle x \right)}^{2}}}\left[ \frac{1}{2}\sum\limits_{j}{\left( {{\eta }_{j}}-{{\eta }_{i}} \right)+\frac{1}{4}\sum\limits_{n}{\left( {{\eta }_{n}}-{{\eta }_{i}} \right)}} \right], $ | (3) |
| $ {{\eta }_{i}}\left( r,t+\Delta t \right)={{\eta }_{i}}\left( r,t \right)+\frac{\text{d}{{\eta }_{i}}\left( r,t \right)}{\text{d}t}\Delta t,i=1,2,\cdots ,P, $ | (4) |
The grain boundary mobility has a direct influence on grain growth during annealing,and the influence of a non-uniform temperature field on grain growth is due to the influence of the non-uniform grain boundary mobility on grain growth. For simplicity,we set a hot zone of uniform temperature and infinite temperature gradient,as shown in Fig. 1. The temperature profile ensures a uniform grain growth within the hot zone and zero growth outside the hot zone. Thus,grain boundary mobility M is given by[23]
| $ M=\left\{ \begin{matrix} {{M}_{\text{h}}},\ \ in\ the\ hot\ zone, \\ 0,\ \ in\ other\ zones, \\ \end{matrix} \right.\ $ | (5) |
A model system is used instead of a specific material,and the parameters used in this study are given in dimensionless units. All calculations are performed on 2D lattice of 512×512 grid points (gp),and periodic boundary conditions are applied. The coefficients in Eqs.(2)-(5) are chosen as follows[15]: α=β=γ=1,k=2,P=36,Mh=1,Δx=2.0,Δt=0.25. In all cases discussed in this study,the hot zone width W is 30 gp,and the hot zone moves along the positive direction of x-axis at a velocity,v=0.002 5 gp·(ts)-1,as shown in Fig. 1.
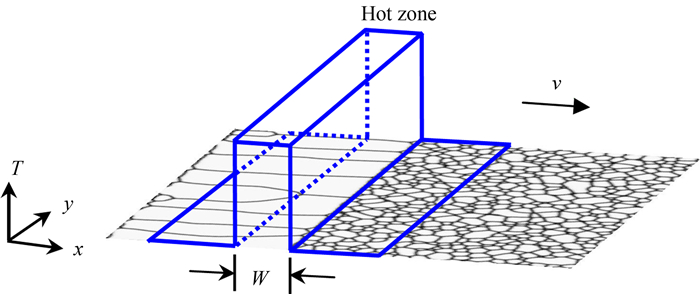 |
| Fig. 1 Schematic illustration of a moving hot zone with infinite temperature (T) gradient[23] |
To visualize the grain microstructure,the following function is defined[15]
| $ \varphi \left( r,t \right)=\sum\limits_{i=1}^{P}{\eta _{i}^{2}\left( r,t \right),} $ | (6) |
Grain growth process is influenced if there exist stable[14, 25] and dispersed SPPs in metals and alloys such as oxide particles,carbide particles[26] which are not easy to decompose or refractory at high temperatures. Since SPPs exert a pinning effect on grain boundaries and thus retard grain growth. In order to study the effect of SPPs on the columnar grain growth,dispersed SPPs were randomly distributed in the initial fine equiaxed grain (the sample) shown in Fig. 2. Directional annealing was performed on the sample. The final grain morphologies after directional annealing are shown in Fig. 3.
 |
| Fig. 2 Initial microstructure[23] |
 |
| Fig. 3 Final microstructures of a system containing different volume fractions of SPPs after directional annealing (a) rp=3gp,fv=0.5% ; (b)rp=3gp,fv=1%; (c) rp=3gp,fv=3%; (d)rp=3gp, fv=8%;(e) rp=1gp,fv=0.5%; (f) rp=1gp,fv=1%; (g) rp=1gp,fv=2%; (h)rp=1gp,fv=3% |
The SPPs radii (rp) in Fig. 3(a)-(d) and Fig. 3(e)-(h) are 3 gp and 1 gp,respectively. It is clear from Fig. 3(a) that the grain structures are almost columnar when the volume fraction of SPPs fv is very low (fv=0.5%). As fv increases,a growing number of SPPs are located at grain boundaries and a mixed structure of elongated and equiaxed grains forms (Fig. 3(b) and (c)). At fv=8%,most grain structures are equiaxed,since most of the grain boundaries are pinned by SPPs. Comparing Fig. 3(c) and (g),it is indicated that smaller SPPs have a stronger pinning effect than larger ones at the same volume fraction and that both grain refinement and uniformity increase with increasing volume fraction of SPPs.
2.2 Effect of SPPs on grain sizeFigure 4 shows the grain size distributions of the system containing different volume fractions of SPPs at rp=1 gp. In the figure,R and R represent grain radius and average grain radius,respectively. The dotted line in Fig. 4 indicates that the grain size is the average grain size R. Note that the greater fv is,the smaller R is. As shown in Fig. 4,when the system does not contain SPPs (fv=0%),most grains (major peak) located at the regions of smaller grain. As fv=1%,the major peak of the grain size distribution is at R/R≈0.5,with a minor peak at R/R> 2 (large abnormal grains). The minor peak is much smaller than that in the case of fv=0%. As fv increases,the peak of the grain size distribution gradually shifts towards 1.0. As fv=4%,the grain size distribution tends to a Gaussian distribution with peak value 1.0,which is consistent with the grain size distribution of normal grain growth[15].
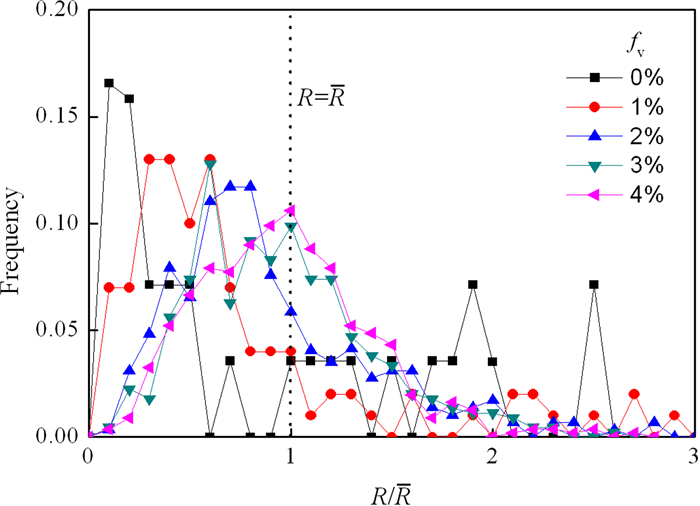 |
| Fig. 4 Grain size distributions of the system containing SPPs at rp=1gp |
At three radii rp the final grain aspect ratio Dx/Dy as functions of fv are plotted in Fig. 5. It is clear that SPPs have an important influence on the final grain aspect ratio. The grain structure in Fig. 3(a) has a high grain aspect ratio (Dx/Dy≈4.8) for fv=0%. As fv increases,the final grain aspect ratio Dx/Dy decreases and gradually converges to 1. The aspect ratio of 1 denotes equiaxed grain. The required volume fractions of SPPs are 8%,5%,and 3% to get a final grain aspect ratio of approximately 1 for rp values of 3,2,and 1 gp,respectively. It is clear that the smaller the SPPs size is,the smaller the SPPs volume fraction for forming an equiaxed grain structure is required. The above results show that the volume fraction of SPPs in polycrystalline materials should be as low as possible in order to obtain better columnar grain structures during directional annealing.
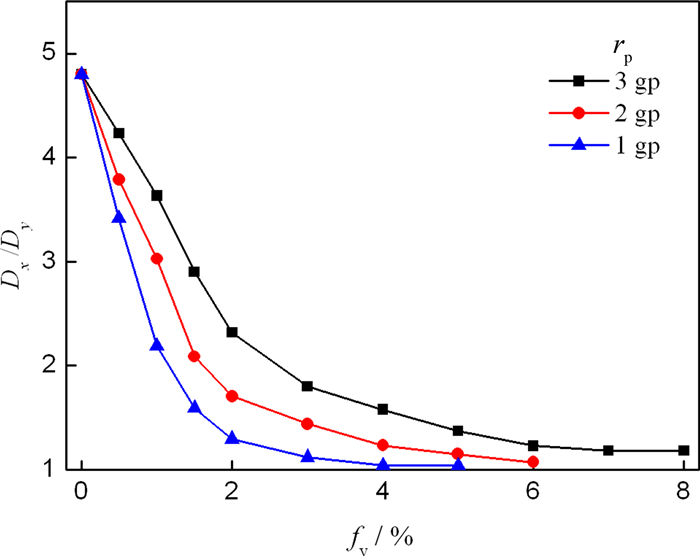 |
| Fig. 5 Final grain aspect ratio Dx/Dy as functions of SPPs volume fraction fv |
The pinning effect of SPPs on grain boundaries influences directly the final grain radius. According to the Zener relation[27],the ratios of final grain radius Rlimto SPPs radius rp as functions of volume fractions fv of the SPPs are shown in Fig. 6. The relations are given by
| $ {{R}_{\lim }}/{{r}_{\text{p}}}=af_{\text{v}}^{-b}=\left\{ \begin{matrix} 46f_{\text{v}}^{-0.45},\ \ \text{for}\ {{r}_{\text{p}}}=1\text{gp}, \\ 28f_{\text{v}}^{-0.47},\ \ \text{for}\ {{r}_{\text{p}}}=2\text{gp}, \\ 23f_{\text{v}}^{-0.48},\ \ \text{for}\ {{r}_{\text{p}}}=3\text{gp}, \\ \end{matrix} \right. $ | (7) |
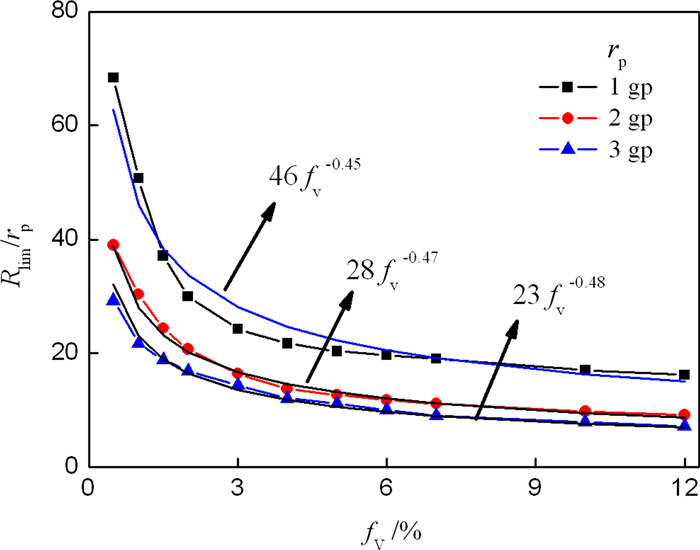 |
| Fig. 6 Ratio of final grain radius Rlimto SPPs radius rp as functions of SPPs volume fraction fv |
SPPs inhibit the formation of columnar grain structure and the inhibitory effect increases with increasing volume fraction of SPPs and decreasing size of SPPs. The smaller the size of SPPs,the smaller the volume fraction of SPPs required for forming an equiaxed grain structure. Under condition of directional annealing,the effect of SPPs on the final grain radius follows the Zener relation in which the fit index is between 0.45 and 0.48. In order to obtain better columnar grain structures during directional annealing,the volume fraction of SPPs and their dispersive distribution at grain boundaries in materials should be reduced as far as possible.
| [1] | HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena[M]. 2nd ed. Oxford:Elsevier, 2004. |
| [2] | HOSFORD W F. Mechanical behavior of materials[M]. Cambridge:Cambridge University Press, 2005. |
| [3] | WAN X, NI H, HUANG M, et al. Microstructure, mechanical properties and creep resistance of Mg-(8%-12%)Zn-(2%-6%)Al alloys[J]. Trans Nonferrous Met Soc China, 2013, 23(4):896-903. |
| [4] | KRILL Ⅲ C E, CHEN L Q. Computer simulation of 3-D grain growth using a phase-field model[J]. Acta Mater, 2002, 50(12):3059-3075. |
| [5] | BAKER I, LI J. Directional annealing of cold-rolled copper single crystals[J]. Acta Mater, 2002, 50(4):805-813. |
| [6] | ZHANG Z W, CHEN G, CHEN G L. Dynamics and mechanism of columnar grain growth of pure iron under directional annealing[J]. Acta Mater, 2007, 55(17):5988-5998. |
| [7] | CAIRNS R L, CURWICK L R, Benjamin J S. Grain growth in dispersion strengthened superalloys by moving zone heat treatments[J]. Metall Trans A, 1975, 6(1):179-188. |
| [8] | GODFREY A W, MARTIN J W. The effect of directional recrystallization on the low cycle fatigue response of a powder metallurgy nickel-based superalloy at elevated temperatures[J]. Mater Sci Eng A, 1997, 222(2):91-100. |
| [9] | HOLM E A, ZACHAROPOULOS N, SROLOVITZ D J. Nonuniform and directional grain growth caused by grain boundary mobility variations[J]. Acta Mater, 1998, 46(3):953-964. |
| [10] | BADMOS A Y, FROST H J, BAKER I. Microstructural evolution during directional annealing[J]. Acta Mater, 2002, 50(13):3347-3359. |
| [11] | BADMOS A Y, FROST H J, BAKER I. Simulation of microstructural evolution during directional annealing with variable boundary energy and mobility[J]. Acta Mater, 2003, 51(10):2755-2764. |
| [12] | WEI C Y, LI S Y. Effect of temperature gradient on grain growth behavior from phase field simulations[J]. Acta Phys Sin, 2011, 60(10):100701. |
| [13] | OHNO M, TSUCHIYA S, MATSUURA K. Formation conditions of coarse columnar austenite grain structure in peritectic carbon steels by the discontinuous grain growth mechanism[J]. Acta Mater, 2011, 59(14):5700-5709. |
| [14] | SUGINO Y, UKAI S, HAYASHI S, et al. Directional recrystallization of ODS alloys by means of zone annealing[J]. J Nucl Mater, 2011, 417(1):171-175. |
| [15] | FAN D, CHEN L Q. Computer simulation of grain growth using a continuum field model[J]. Acta Mater, 1997, 45(2):611-622. |
| [16] | CHEN L Q. Phase-field models for microstructure evolution[J]. Annu Rev Mater Res, 2002, 32(1):113-140. |
| [17] | BOETTINGER W J, WARREN J A, BECKERMANN C, et al. Phase-field simulation of solidification[J]. Annu Rev Mater Res, 2002, 32(1):163-194. |
| [18] | GAO Y J, LUO Z R, HU X Y, et al. Phase field simulation of static recrystallization for AZ31 Mg alloy[J]. Acta Metall Sin, 2010, 46(10):1161-1172. |
| [19] | KIM S G, KIM D I, KIM W T, et al. Computer simulations of two-dimensional and three-dimensional ideal grain growth[J]. Phys Rev E, 2006, 74(6):61605. |
| [20] | SPATSCHEK R, HARTMANN M, BRENER E, et al. Phase field modeling of fast crack propagation[J]. Phys Rev Lett, 2006, 96(1):15502. |
| [21] | GAO Y J, LUO Z R, DENG Q Q, et al. Phase-field-crystal modeling of microcrack propagation and branching in ductile materials[J]. Chinese J Comput Phys, 2014, 31(4):471-479. |
| [22] | LUO Z R, LIU Y, DENG Q Q, et al. Phase field study of the formation of columnar-grain structure during directional annealing[J]. Guangxi Phys, 2013, 34(1):9-13. |
| [23] | LUO Z R, GAO Y J, DENG Q Q, et al. Phase field modeling for the formation and continued propagation of columnar grain structure during directional annealing[J]. Chinese J Nonferrous Metals, 2014, 24(7):1778-1784. |
| [24] | MOELANS N, BLANPAIN B, WOLLANTS P. Phase field simulations of grain growth in two-dimensional systems containing finely dispersed second-phase particles[J]. Acta Mater, 2006, 54(4):1175-1184. |
| [25] | KOZIEJ D, LAURIA A, NIEDERBERGER M. 25th anniversary article:Metal oxide particles in materials science:Addressing all length scales[J]. Adv Mater, 2014, 26(2):235-257. |
| [26] | CHEE C Y, AZMI A. Preparation and characterization of copper/copper coated silicon carbide composites[J]. Int J Precis Eng Man, 2014, 15(6):1215-1221. |
| [27] | MANOHAR P A, FERRY M, CHANDRA T. Five decades of the Zener equation[J]. ISIJ Int, 1998, 38(9):913-924. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

