中国工程物理研究院总体工程研究所, 四川 绵阳 621900
Institute of Systems Engineering, CAEP, Mianyang Sichuan 621900, China
0 引言
有限元法基本思想是将一个连续体的求解域离散为若干子域,并通过边界上的节点连接成为组合体,用每个单元内的近似函数来表示求解域内的未知场变量,通过和原问题数学模型等效的变分原理或加权余量法,建立代数方程组以求解基本未知量[1].
传统线性有限元直接以数学为基础采用双线性多项式构造形函数,其位移模式没有考虑弹性力学控制方程,也不能反映不同自由度间位移的相互影响,单元精度较低.为改善计算精度,上世纪90年代钟万勰院士团队研发了理性有限元,核心思想是从弹性力学出发建立位移模式,其插值函数的各项均来源于弹性力学精确解,有明确的物理意义[2, 3, 4, 5, 6, 7].但理性有限元形函数繁复,给实际操作带来很大困难[8, 9].近年来,张洪武教授团队在理性有限元的基础上,进一步发展了广义有限元方法,核心思想是改变传统有限元只利用单元节点同方向自由度的位移构造方式,以单元所有节点自由度来构造单元位移[10, 11],其位移模式仍沿用了传统有限元的多项式插值函数,并没有有效利用弹性力学解.
本文针对平面应变问题,提出一种广义四边形单元,综合考虑理性有限元和广义有限元的优势,从弹性力学平面应变方程出发建立形函数,并在不改变单元自由度的情况下为形函数引入位移附加项,提高了单元计算精度.由于新单元只在传统有限元基础上增加位移附加项形函数,因此程序操作简单易于实现.
1 平面应变新型广义四边形单元
1.1 一般单元
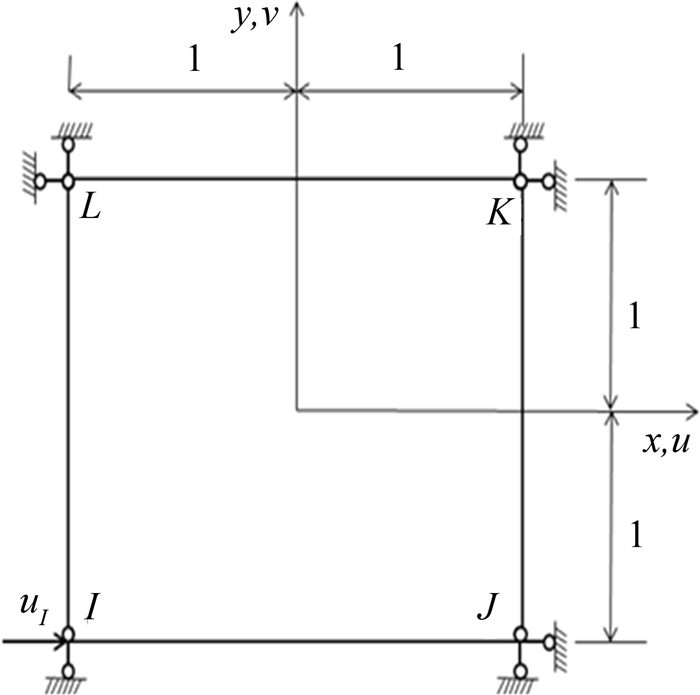
传统平面矩形单元具有4个节点8自由度,如图 1所示.用4个节点位移表达的位移模式为
|
$
\left\{ \begin{matrix}
u={{N}_{1}}{{u}_{I}}+{{N}_{2}}{{u}_{J}}+{{N}_{3}}{{u}_{K}}+{{N}_{4}}{{u}_{L}}, \\
v={{N}_{1}}{{v}_{I}}+{{N}_{2}}{{v}_{J}}+{{N}_{3}}{{v}_{K}}+{{N}_{4}}{{v}_{L}} \\
\end{matrix} \right.
$
|
(1)
|
其中插值函数为双线性函数
|
$
\left\{ \begin{matrix}
{{N}_{1}}=\left( 1-x \right)\left( 1-y \right)/4,\ {{N}_{2}}=\left( 1+x \right)\left( 1-y \right)/4, \\
{{N}_{3}}=\left( 1+x \right)\left( 1+y \right)/4,\ {{N}_{4}}=\left( 1-x \right)\left( 1+y \right)/4, \\
\end{matrix} \right.
$
|
(2)
|
可见其形函数的构造完全基于数学层面,且位移模式中只包含节点同方向自由度,计算精度较低.
由泊松效应可知,一个方向的变形将引起另一个方向的位移.本文拟开发的广义平面应变四边形单元考虑弹性体的泊松效应,由单元的所有自由度构造单元位移模式,即单元内任意一点的位移分量不仅和四个节点位移分量方向的节点自由度相关,同样和四个节点处位移分量方向正交的节点自由度相关.该思想与广义有限元[10, 11]一致,与其不一样的是,在建立形函数时,借鉴理性有限元思想,在传统有限元位移模式的基础上,根据节点位移自由度约束弹性力学平面应变方程确定单元位移模式的附加项.新平面四边形单元的位移模式既考虑了节点上所有的自由度,又考虑了弹性力学控制方程,能较准确反映真实位移场,因此有更高的计算精度.以下将针对平面应变情况进行形函数构造.
对于位移模式(1),节点自由度确定了单元节点边界条件
|
$
\left\{ \begin{matrix}
u\left( -1,-1 \right)={{u}_{I}},\ \ u\left( 1,-1 \right)={{u}_{J}},\ \ u\left( 1,1 \right)={{u}_{K}},\ \ u\left( -1,1 \right)={{u}_{L}}, \\
v\left( -1,-1 \right)={{v}_{I}},\ \ v\left( 1,-1 \right)={{v}_{J}},\ \ v\left( 1,1 \right)={{v}_{K}},\ \ v\left( -1,1 \right)={{v}_{L}}. \\
\end{matrix} \right.
$
|
(3)
|
为了考察一个自由度对另一自由度位移影响,以第一个节点的
x方向自由度为例,分析其它节点自由度固定仅在节点
I施加
x方向位移
uI时对
y方向位移的贡献,如
图 1所示.满足上述节点位移的条件
|
$
\left\{ \begin{matrix}
u\left( -1,-1 \right)={{u}_{I}},\ \ u\left( 1,-1 \right)=\ u\left( 1,1 \right)=u\left( -1,1 \right)=0, \\
v\left( -1,-1 \right)=v\left( 1,-1 \right)=\ v\left( 1,1 \right)=v\left( -1,1 \right)=0. \\
\end{matrix} \right.\
$
|
(4)
|
线弹性平面应变问题的齐次位移平衡微分方程为
|
$
\left\{ \begin{matrix}
2\left( 1-\mu \right)\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\left( 1-2\mu \right)\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}v}{\partial x\partial y}=0, \\
\left( 1-2\mu \right)\frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+2\left( 1-\mu \right)\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}u}{\partial x\partial y}=0. \\
\end{matrix} \right.
$
|
(5)
|
取满足式(4)第一行方程的形函数基为
|
$
{{u}_{1}}\left( x,y \right)=\frac{1}{4}{{u}_{I}}\left( 1-x \right)\left( 1-y \right),
$
|
(6)
|
将式(6)代入式(5)的第一个方程有
|
$
\frac{{{\partial }^{2}}v}{\partial x\partial y}=0;
$
|
(7)
|
式(6)代入式(5)的第二个方程且考虑节点边界条件有
|
$
\left\{ \begin{matrix}
\left( 1-2\mu \right)\frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+2\left( 1-\mu \right)\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}}+\frac{1}{4}{{u}_{I}}=0, \\
v\left( -1,-1 \right)=v\left( 1,-1 \right)=\ v\left( 1,1 \right)=v\left( -1,1 \right)=0, \\
\end{matrix} \right.
$
|
(8)
|
上式结合式(7)可假设第一个自由度
uI产生的
y方向的位移表达式为
|
$
{{v}_{1}}\left( x,y \right)={{b}_{0}}+{{b}_{1}}x+{{b}_{2}}y+{{b}_{3}}{{x}^{2}}+{{b}_{4}}{{y}^{2}},
$
|
(9)
|
代入式(8)得到关系式
|
$
\left\{ \begin{matrix}
{{b}_{1}}={{b}_{2}}=0, \\
{{b}_{3}}=2\left( \mu -1 \right){{b}_{0}}+\frac{1}{8}{{u}_{I}}, \\
{{b}_{4}}=\left( 1-2\mu \right){{b}_{0}}-\frac{1}{8}{{u}_{I}}. \\
\end{matrix} \right.\
$
|
(10)
|
考虑到位移
v1完全由节点位移
uI引起,可设
b0=
βuI则位移
|
$
{{v}_{1}}\left( x,y \right)=\left\{ \beta +\left[ 2\left( \mu -1 \right)\beta +\frac{1}{8} \right]{{x}^{2}}+\left[ \left( 1-2\mu \right)\beta -\frac{1}{8} \right]{{y}^{2}} \right\}{{u}_{I}},
$
|
(11)
|
代入坐标(0,0)可得
|
$
{{v}_{1}}\left( 0,0 \right)=\beta {{u}_{I}}.
$
|
(12)
|
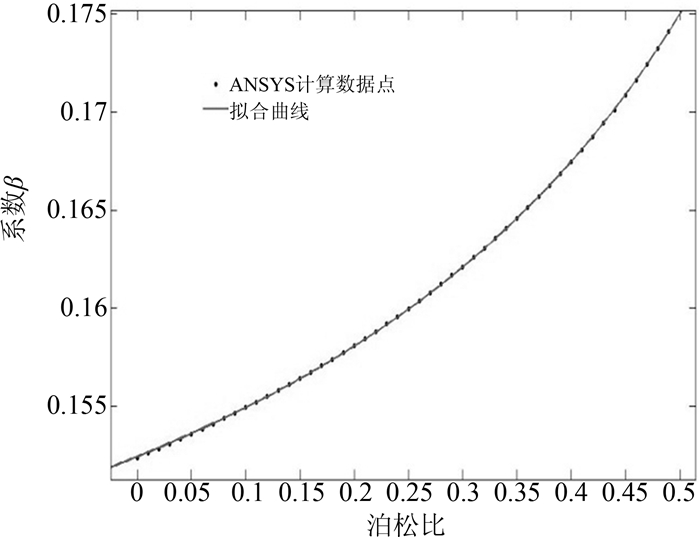
式(12)表明,位移
v1中的常数项是由于泊松效应,由单元节点自由度位移分量引起的单元中心点该位移分量正交方向上的位移.通过ANSYS有限元计算并采用响应面方法,拟合得到系数
β与泊松比
μ的关系
|
$
\beta =\frac{0.02251}{1-\mu }+0.1299.
$
|
(13)
|
式(13)的数据拟合图如
图 2所示.
将式(13)代入式(11)有
|
$
{{v}_{1}}\left( x,y \right)=[{{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right)]{{u}_{I}},\
$
|
(14)
|
其中
|
$
\left\{ \begin{matrix}
{{c}_{1}}=-2\left( \mu -1 \right)\left( \frac{0.02251}{1-\mu }+0.1299 \right)-\frac{1}{8}, \\
{{c}_{2}}=\left( 2\mu -1 \right)\left( \frac{0.02251}{1-\mu }+0.1299 \right)+\frac{1}{8}. \\
\end{matrix} \right.
$
|
(15)
|
同理,其它自由度的位移
vi可表达为
|
$
\left\{ \begin{matrix}
{{v}_{2}}\left( x,y \right)=-\left[ {{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right) \right]{{u}_{J}}, \\
{{v}_{3}}\left( x,y \right)=\left[ {{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right) \right]{{u}_{K}}, \\
{{v}_{4}}\left( x,y \right)=-\left[ {{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right) \right]{{u}_{L}}. \\
\end{matrix} \right.
$
|
(16)
|
施加
x方向节点位移约束将产生
y方向的位移,可以看作是
x方向位移对
y方向位移的贡献.综合考虑四个节点的位移附加项可得到位移
|
$
v={{N}_{1}}{{v}_{I}}+{{N}_{2}}{{v}_{J}}+{{N}_{3}}{{v}_{K}}+{{N}_{4}}{{v}_{L}}+{{N}_{5}}\left( {{u}_{I}}+{{u}_{K}} \right)+{{N}_{6}}\left( {{u}_{J}}+{{u}_{L}} \right),
$
|
(17)
|
其中,
|
$
\left\{ \begin{matrix}
{{N}_{5}}={{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right), \\
{{N}_{6}}=-\left[ {{c}_{1}}\left( 1-{{x}^{2}} \right)+{{c}_{2}}\left( 1-{{y}^{2}} \right) \right]. \\
\end{matrix} \right.
$
|
(18)
|
同理,水平位移
u的最终表达式为
|
$
u={{N}_{1}}{{u}_{I}}+{{N}_{2}}{{u}_{J}}+{{N}_{3}}{{u}_{K}}+{{N}_{4}}{{u}_{L}}+{{N}_{7}}\left( {{v}_{I}}+{{v}_{K}} \right)+{{N}_{8}}\left( {{v}_{J}}+{{v}_{L}} \right),\
$
|
(19)
|
其中,
|
$
\left\{ \begin{matrix}
{{N}_{7}}={{c}_{2}}\left( 1-{{x}^{2}} \right)+{{c}_{1}}\left( 1-{{y}^{2}} \right), \\
{{N}_{8}}=-\left[ {{c}_{2}}\left( 1-{{x}^{2}} \right)+{{c}_{1}}\left( 1-{{y}^{2}} \right) \right]. \\
\end{matrix} \right.
$
|
(20)
|
写成矩阵表达式为
|
$
\left[ \begin{matrix}
u \\
v \\
\end{matrix} \right]=\left[ \begin{matrix}
{{N}_{1}}\ \ {{N}_{7}}\ \ {{N}_{2}}\ \ {{N}_{8}}\ \ {{N}_{3\ \ }}{{N}_{7}}\ \ {{N}_{4}}\ \ {{N}_{8}} \\
{{N}_{5}}\ \ {{N}_{1}}\ \ {{N}_{6}}\ \ {{N}_{2}}\ \ {{N}_{5\ \ }}{{N}_{3}}\ \ {{N}_{6}}\ \ {{N}_{4}} \\
\end{matrix} \right]{{\left[ {{u}_{I}}\ {{v}_{I}}\ {{u}_{J}}\ {{v}_{J}}\ {{u}_{K}}\ {{v}_{K}}\ {{u}_{L}}\ {{v}_{L}} \right]}^{\text{T}}}.\
$
|
(21)
|
可以证明在各节点处,
N1=
N2=
N3=
N4=1,
N5=
N6=
N7=
N8=0,满足插值函数的Kronecker delta 性质;单元中任一点
N1+
N2+
N3+
N4=1,
N5+
N6=0,
N7+
N8=0,满足插值函数的归一性质.
1.2 等参单元
传统等参元中整体坐标与局部坐标的映射关系为
|
$
\left\{ \begin{matrix}
x'={{N}_{1}}x_{I}^{'}+{{N}_{2}}x_{J}^{'}+{{N}_{3}}x_{K}^{'}+{{N}_{4}}x_{L}^{'}, \\
y'={{N}_{1}}y_{I}^{'}+{{N}_{2}}y_{J}^{'}+{{N}_{3}}y_{K}^{'}+{{N}_{4}}y_{L}^{'}, \\
\end{matrix} \right.
$
|
(22)
|
其中
N1,
N2,
N3,
N4为式(2)在局部坐标系下表达式.根据1.1中思路可写出平面应变问题新型广义等参元位移模式
|
$
\left\{ \begin{matrix}
u'={{N}_{1}}u_{I}^{'}+{{N}_{2}}u_{J}^{'}+{{N}_{3}}u_{K}^{'}+{{N}_{4}}u_{L}^{'}+{{N}_{9}}v_{I}^{'}+{{N}_{10}}v_{J}^{'}+{{N}_{11}}v_{K}^{'}+{{N}_{12}}v_{L}^{'}, \\
v'={{N}_{1}}v_{I}^{'}+{{N}_{2}}v_{J}^{'}+{{N}_{3}}v_{K}^{'}+{{N}_{4}}v_{L}^{'}+{{N}_{5}}u_{I}^{'}+{{N}_{6}}u_{J}^{'}+{{N}_{7}}u_{K}^{'}+{{N}_{8}}u_{L}^{'}, \\
\end{matrix} \right.
$
|
(23)
|
其中各附加等参形函数为
|
$
\left\{ \begin{matrix}
{{N}_{5}}={{\beta }_{1}}\left[ {{c}_{1}}\left( 1-{{\xi }^{2}} \right)+{{c}_{2}}\left( 1-{{\eta }^{2}} \right) \right],\ \ {{N}_{6}}=-{{\beta }_{2}}\left[ {{c}_{1}}\left( 1-{{\xi }^{2}} \right)+{{c}_{2}}\left( 1-{{\eta }^{2}} \right) \right], \\
{{N}_{7}}={{\beta }_{3}}\left[ {{c}_{1}}\left( 1-{{\xi }^{2}} \right)+{{c}_{2}}\left( 1-{{\eta }^{2}} \right) \right],\ \ {{N}_{8}}=-{{\beta }_{4}}\left[ {{c}_{1}}\left( 1-{{\xi }^{2}} \right)+{{c}_{2}}\left( 1-{{\eta }^{2}} \right) \right], \\
{{N}_{9}}={{\beta }_{1}}\left[ {{c}_{2}}\left( 1-{{\xi }^{2}} \right)+{{c}_{1}}\left( 1-{{\eta }^{2}} \right) \right],\ \ {{N}_{10}}=-{{\beta }_{2}}\left[ {{c}_{1}}\left( 1-{{\xi }^{2}} \right)+{{c}_{2}}\left( 1-{{\eta }^{2}} \right) \right], \\
{{N}_{11}}={{\beta }_{3}}\left[ {{c}_{2}}\left( 1-{{\xi }^{2}} \right)+{{c}_{1}}\left( 1-{{\eta }^{2}} \right) \right],\ \ {{N}_{12}}=-{{\beta }_{4}}\left[ {{c}_{2}}\left( 1-{{\xi }^{2}} \right)+{{c}_{1}}\left( 1-{{\eta }^{2}} \right) \right], \\
\end{matrix} \right.
$
|
(24)
|
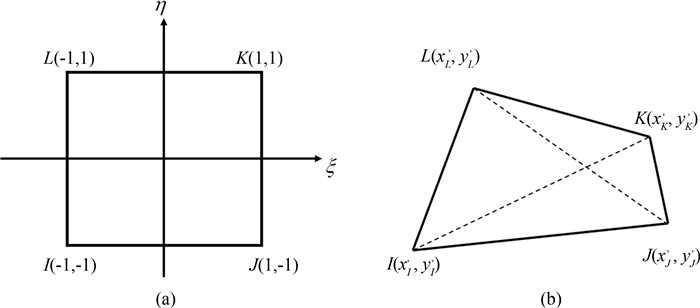
式中的面积系数
βi与单元节点所围三角形面积相关.定义
图 3(b)中
SΔ
IJK为三角形Δ
IJK的面积,S为四边形总面积,于是可定义具体表达形式如下
|
$
{{\beta }_{1}}=2S\vartriangle JKL/S,{{\beta }_{2}}=2S\vartriangle KLI/S,\ {{\beta }_{3}}=2S\vartriangle LIJ/S,\ {{\beta }_{4}}=2S\vartriangle ILK/S.
$
|
(25)
|
在标准单元中
β1=
β2=
β3=
β4=1.至此平面应变问题新型广义等参单元的位移函数已给出,剩下的求解过程与传统的等参元相同.
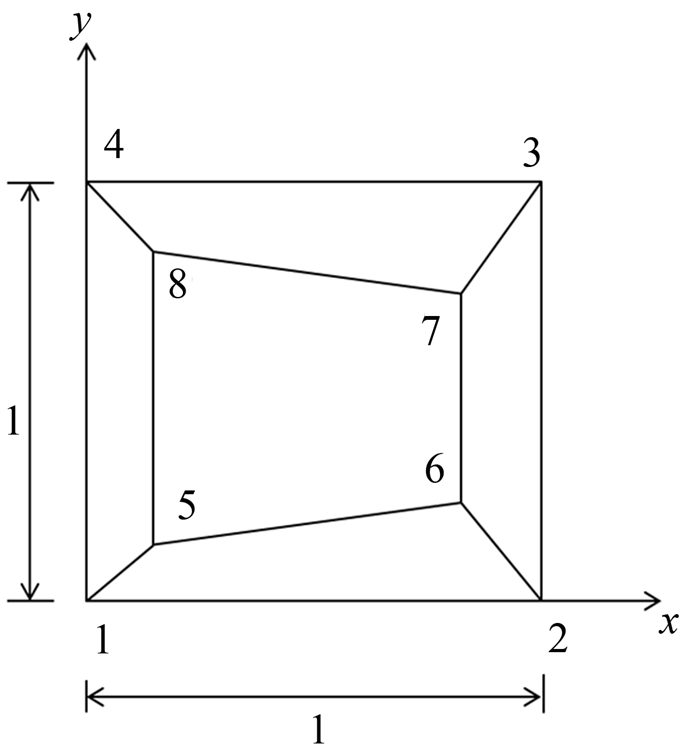
2 分片试验
对平面应变问题新型广义等参四边形单元收敛性进行分片测试.分片单元如图 4所示.刚体位移测试:假定刚体位移模式为u=1,v=1,即在所有外节点处
|
$
\left\{ \begin{matrix}
{{u}_{1}}={{u}_{2}}={{u}_{3}}={{u}_{4}}=1, \\
{{v}_{1}}={{v}_{2}}={{v}_{3}}={{v}_{4}}=1. \\
\end{matrix} \right.
$
|
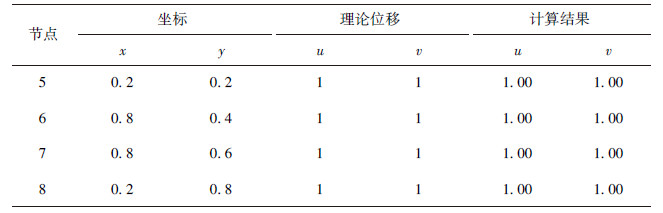
求内部节点5,6,7,8的位移.计算结果见表 1,结果表明新单元能通过刚体位移测试.
表1(Table 1)
|
表1 刚体位移分片测试测试结果
Table 1 Rigid body displacement test results for patch test
|
表1 刚体位移分片测试测试结果
Table 1 Rigid body displacement test results for patch test
| 节点 |
坐标 |
|
理论位移 |
|
计算结果 |
| x |
y |
u |
v |
u |
v |
| 5 |
0.2 |
0.2 |
|
1 |
1 |
|
1.00 |
1.00 |
| 6 |
0.8 |
0.4 |
1 |
1 |
1.00 |
1.00 |
| 7 |
0.8 |
0.6 |
1 |
1 |
1.00 |
1.00 |
| 8 |
0.2 |
0.8 |
1 |
1 |
1.00 |
1.00 |
|
 |
| 点击放大 |
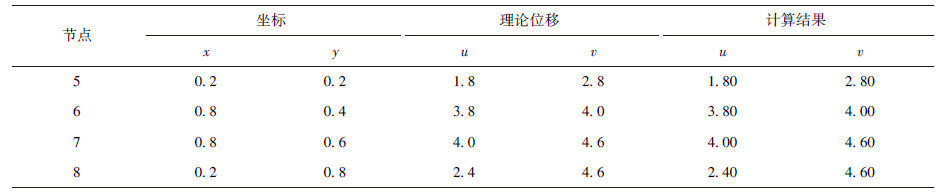
常应变测试:对边界上的节点给以常应变位移场
采用一个Gauss积分点方案,内部节点位移结果列于表 2,结果表明新单元通过常应变测试.
表2(Table 2)
|
表2 常应变分片测试结果
Table 2 Constant strain test results for patch test
|
表2 常应变分片测试结果
Table 2 Constant strain test results for patch test
| 节点 |
坐标 |
|
理论位移 |
|
计算结果 |
| x |
y |
u |
v |
u |
v |
| 5 |
0.2 |
0.2 |
|
1.8 |
2.8 |
|
1.80 |
2.80 |
| 6 |
0.8 |
0.4 |
3.8 |
4.0 |
3.80 |
4.00 |
| 7 |
0.8 |
0.6 |
4.0 |
4.6 |
4.00 |
4.60 |
| 8 |
0.2 |
0.8 |
2.4 |
4.6 |
2.40 |
4.60 |
|
 |
| 点击放大 |
3 数值算例
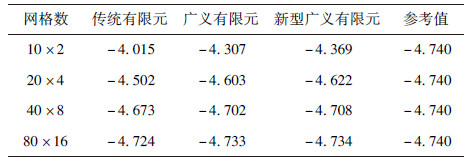
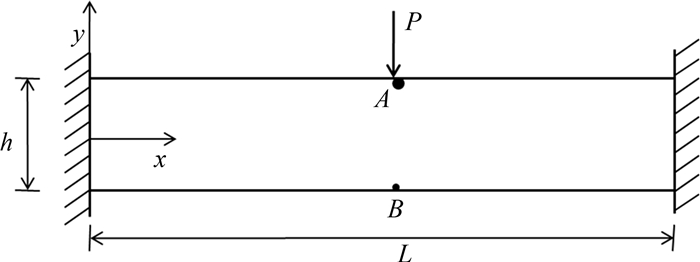
算例1 该算例采用模型如图 5所示,长L=0.1 m,高h=0.02 m,材料常数E=2.1×1011 Pa,泊松比μ=0.3.结构两端所有节点两个自由度均约束,中点A受向下的压力P=1×107 N的作用.对新型广义有限元、广义有限元和传统有限元三种单元用不同密度的网格进行B点竖直位移计算结果比较.参考值是网格数加密到160×32所得位移值.
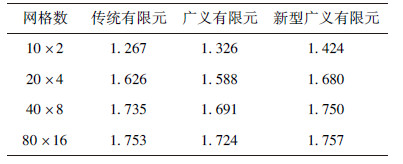
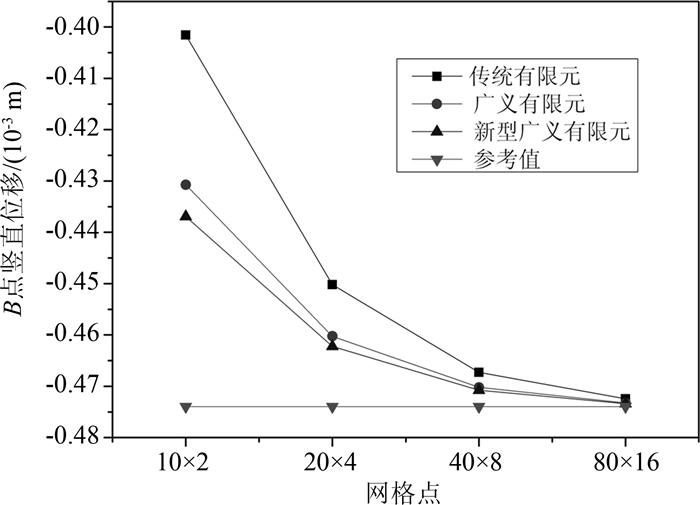
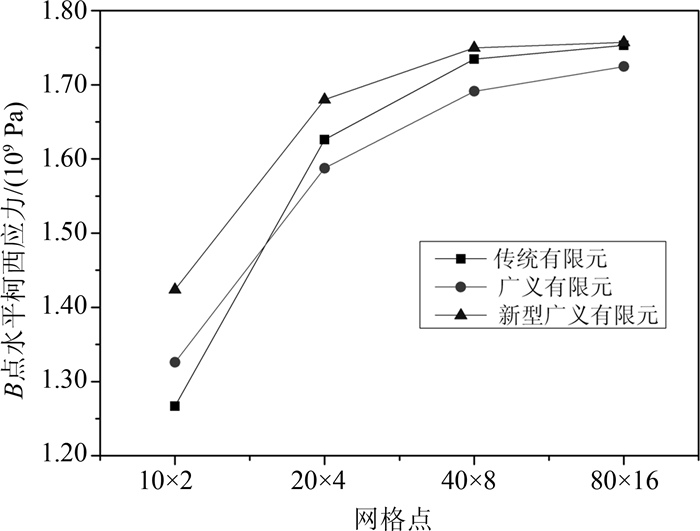
平面应变情况下不同网格密度计算所得B点竖直位移对比如表 3所示,随网格加密的收敛曲线如图 6所示;B点水平柯西应力对比值见表 4,相应的应力收敛曲线见图 7.结果表明,在平面应变情况下,相比于传统有限元和广义有限元,同一网格密度新型广义四边形单元计算精度有所提高.
表3(Table 3)
|
表3 平面应变下B点竖直位移值(单位:10-4 m)
Table 3 Vertical displacement of point B in plane strain condition(unit: 10-4 m)
|
表3 平面应变下B点竖直位移值(单位:10-4 m)
Table 3 Vertical displacement of point B in plane strain condition(unit: 10-4 m)
| 网格数 |
传统有限元 |
广义有限元 |
新型广义有限元 |
参考值 |
| 10×2 |
-4.015 |
-4.307 |
-4.369 |
-4.740 |
| 20×4 |
-4.502 |
-4.603 |
-4.622 |
-4.740 |
| 40×8 |
-4.673 |
-4.702 |
-4.708 |
-4.740 |
| 80×16 |
-4.724 |
-4.733 |
-4.734 |
-4.740 |
|
 |
| 点击放大 |
表4(Table 4)
|
表4 平面应变下 B点水平柯西应力值(单位: 109 Pa)
Table 4 Horizontal Cauchy stress of point B in plane strain condition(unit: 109 Pa)
|
表4 平面应变下 B点水平柯西应力值(单位: 109 Pa)
Table 4 Horizontal Cauchy stress of point B in plane strain condition(unit: 109 Pa)
| 网格数 |
传统有限元 |
广义有限元 |
新型广义有限元 |
| 10×2 |
1.267 |
1.326 |
1.424 |
| 20×4 |
1.626 |
1.588 |
1.680 |
| 40×8 |
1.735 |
1.691 |
1.750 |
| 80×16 |
1.753 |
1.724 |
1.757 |
|
 |
| 点击放大 |
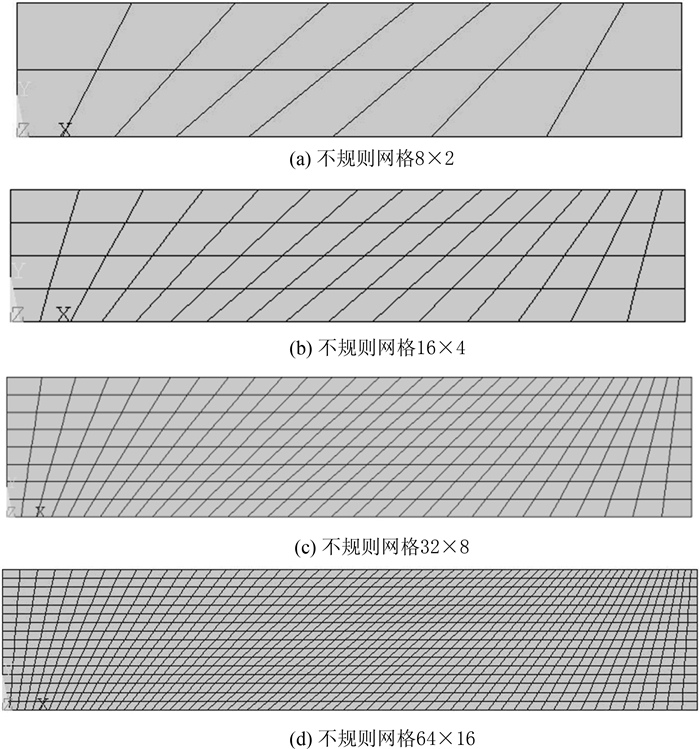
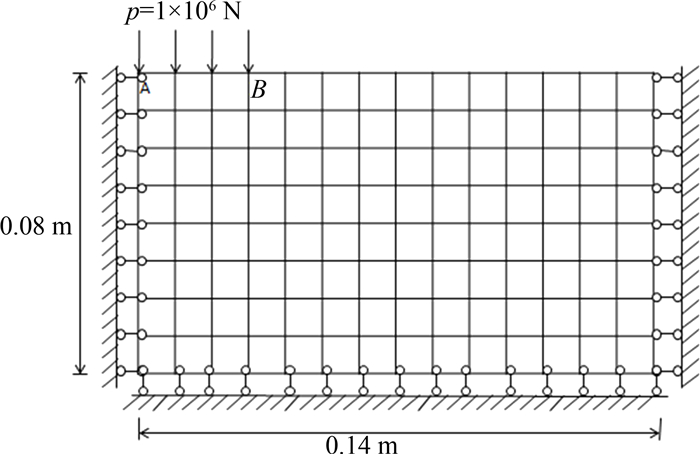
算例2 该算例采用模型如图 8所示,长L=10 cm,高h=2 cm,材料常数E=2.1×105 MPa,泊松比μ=0.3.结构左端所有节点两个方向自由度均固定,右端受向下剪力P=1 000 N的作用,剪力P集中加载在右端中点A.对新型广义有限元、广义有限元和传统有限元三种单元用不同密度的不规则网格进行B点竖直位移计算结果比较.不规则划分结果见图 9(a)-(d).
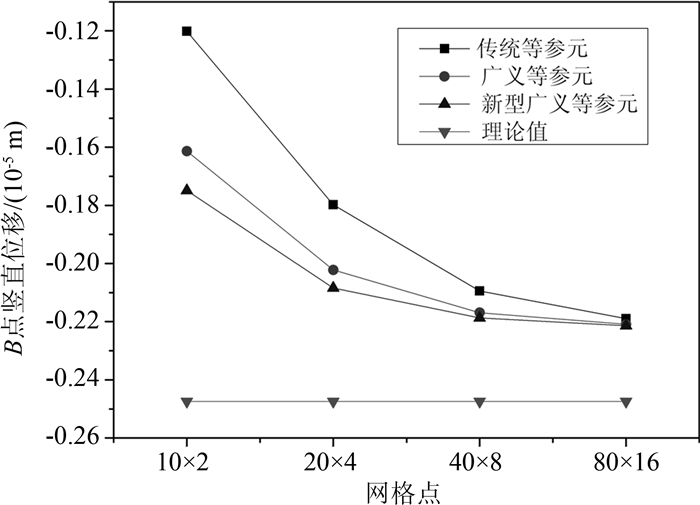
不同密度网格下B点竖直位移值见表 5,随网格加密位移收敛曲线图如图 10所示.计算结果表明在不规则网格下新型广义等参单元计算精度仍高于广义等参单元和传统等参元.
表5(Table 5)
|
表5 平面应变下不规则网格划分 B点竖直位移值(单位:10-6 m)
Table 5 Vertical displacement of point B with irregular grid in plane strain condition (unit: 10-6 m)
|
表5 平面应变下不规则网格划分 B点竖直位移值(单位:10-6 m)
Table 5 Vertical displacement of point B with irregular grid in plane strain condition (unit: 10-6 m)
| 网格数 |
传统等参元 |
广义等参元 |
新型广义等参元 |
理论值 |
| 8×2 |
-1.202 |
-1.613 |
-1.749 |
-2.474 |
| 16×4 |
-1.797 |
-2.022 |
-2.085 |
-2.474 |
| 32×8 |
-2.094 |
-2.169 |
-2.187 |
-2.474 |
| 64×16 |
-2.189 |
-2.209 |
-2.214 |
-2.474 |
|
 |
| 点击放大 |
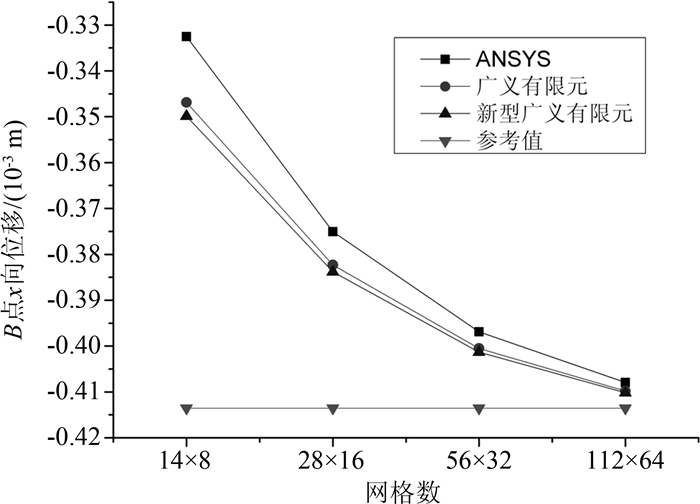
算例3 如图 11所示结构,结构下表面所有节点固定y方向位移,左侧和右侧所有节点固定x方向位移,在结构上表面左侧AB段加载P=1×1010 N的均布向下荷载,材料属性和算例1一致.三种单元用不同密度的网格进行计算.参考值为网格加密到224×128所得值.
表 6列出不同网格下B点水平位移值,随网格加密位移曲线如图 12所示.结果同样表明相比于传统有限元和广义有限元,同一网格密度新型广义四边形单元计算精度有所提高.
表6(Table 6)
|
表6 平面应变下B点水平位移值(单位:10-4 m)
Table 6 Horizontal displacement of point B in plane strain condition(unit:10-4 m)
|
表6 平面应变下B点水平位移值(单位:10-4 m)
Table 6 Horizontal displacement of point B in plane strain condition(unit:10-4 m)
| 网格数 |
传统有限元 |
广义有限元 |
新型广义有限元 |
参考值 |
| 14×8 |
-3.325 |
-3.469 |
-3.499 |
-4.135 |
| 28×16 |
-3.751 |
-3.823 |
-3.838 |
-4.135 |
| 56×32 |
-3.969 |
-4.005 |
-4.013 |
-4.135 |
| 112×64 |
-4.080 |
-4.098 |
-4.102 |
-4.135 |
|
 |
| 点击放大 |
4 结论
从弹性力学平面应变方程出发推导形函数,同时在插值函数中引入位移附加项,建立了平面应变问题一种四边形单元.由于位移插值函数综合考虑弹性力学平面应变方程和泊松效应,较真实地反映了单元位移场,其计算精度得以提高.在位移附加项中引入面积系数,建立了平面应变广义等参四边形单元.新等参单元能收敛于真实解,数值算例表明其计算精度高于传统等参四边形单元和广义等参四边形单元,且收敛速度更快.
本方法在传统的形函数上增加了位移附加项,没有增加单元自由度,程序修改简单,实现方便,易于推广.今后将在三维新型广义单元方面进一步开展研究,以提高新单元对实际工程的应用范围.








 2016, Vol. 33
2016, Vol. 33
