| 一种热集成系统的动态多智能体微分进化算法 |
换热网络优化问题即在满足物流目标出口温度的前提下,如何充分利用换热网络内的能量,使系统回收的能量最大或投资运行费用最小[1].
针对换热网络优化问题,国内外学者做了大量的工作,其研究成果可分为热力学方法和数学规划法两类.其中热力学方法主要为Linnholf等提出的夹点技术法[2],这种热力学方法具有物理意义清晰、操作简单等优点,但在全局优化上有一定的不足.而数学规划法则是在Cerda建立的换热网络数学模型基础上应用数学优化方法找全局最优解 [3],其全局收敛性在一定程度上强于热力学方法[4, 5].对于换热网络优化问题,其优化变量既包括换热器面积及公用工程用量的连续变量,也包括表示换热器有无的0-1整型变量.因此换热网络综合问题属于典型混合整数非线性问题(Mixed Integer Nonlinear Program,MINLP),在整个求解域内存在着大量的局部最优解,而且随着化工系统规模的不断扩大,换热网络优化问题的求解难度也急剧上升.所以采用传统的局部优化方法,极易陷入局部极值陷阱.
基于此,更适用于解决实际问题的启发式方法被提出并应用于换热网络优化问题.启发式方法具有的随机性使其具有很强的全局搜索能力,不会因为问题的非凸非线性而陷入局部最优解,因此启发式方法逐渐成为适用于解决换热网络全局最优化问题的一类主流算法.微分进化(Differential Evolution)算法是新近提出的一种智能优化方法,已经被证明在求优过程中具有高效性、收敛性好、鲁棒性高等优点[6, 7, 8].DE算法采用实数分量合成参数矢量的方法,进化过程控制变量较少,而且采用的变异操作具有遗传算法所不具备的微调功能,在换热网络优化中已初步得到应用[9].
微分进化算法在解决换热网络优化等大规模复杂工程问题过程中,影响其搜索能力和实用性的关键因素之一就是搜索空间的不断扩大.而多智能体算法以其感知环境并反作用于环境的特点表现出较大的智能特性,在对复杂问题尤其在高位问题的求解中表现出色,并广泛应用于各个学科领域[10, 11, 12].本文针对换热网络优化问题,将智能体对环境的感知和反作用环境的能力与微分进化算法相结合,并引入动态更新策略,提出动态多智能体微分进化算法(Dynamic multi-agent difference evolution,DMADE),利用多智能体的概念和特性改进微分进化算法的种群生成原则与个体变异机制,同时使整个种群在进化过程中动态更新,在不增加新的控制参数的情况下,改进并很好地利用了原DE算法的种群多样性,针对仿真测试函数与换热网络问题优化都体现出很好的效果,充分显示方法的实用价值,同时也显示出智能体与进化算法相结合的巨大潜力.
1 换热网络问题 1.1 换热网络问题描述假设有NC股冷流体需要加热,NH股热流体需要冷却,换热网络就是利用冷、热物流的匹配,回收过程流体的能量.已知冷、热物流的进口温度、目标温度、热容流率及各换热器换热系数,同时,为未达到目标温度的流体设置热、冷公用工程,公用工程的进、出口温度已知.根据冷、热流体的匹配顺序形成一个换热网络,在所有网络流体达到目标温度的情况下,最小化换热网络的投资费用与运行费用.投资费用包括换热器固定投资费用与换热器面积费用,运行费用为公用工程的消耗量.本文的换热网络结构的表达方式为Grossmann无分流分级结构模型[13],其中,换热网络级数为NK,最大换热器个数为NK×NC×NH.以二股热流体与三股冷流体为例,其分级超结构模型如图 1所示.
 |
| 图1 换热网络无分流的分级超结构 Fig. 1 Superstructure of heat exchanger networks with no stream splits |
换热网络优化问题的目标函数为年综合费用,包括投资费用与运行费用.其数学表达为
| $ \begin{matrix} F={{F}_{\text{EX}}}+{{F}_{\text{HU}}}+{{F}_{\text{CU}}}+{{F}_{\text{A}}}={{C}_{0}}\sum\limits_{k=1}^{{{N}_{\text{K}}}}{\sum\limits_{i=1}^{{{N}_{\text{H}}}}{\sum\limits_{j=1}^{{{N}_{\text{C}}}}{{{Z}_{k,i,j}}+\sum\limits_{i=1}^{{{N}_{\text{H}}}}{{{\left( {{C}_{1}}ZQ \right)}_{HUi}}}+\sum\limits_{i=1}^{{{N}_{\text{C}}}}{{{\left( {{C}_{1}}ZQ \right)}_{HUi}}+}}}} \\ \sum\limits_{k=1}^{{{N}_{\text{K}}}}{\sum\limits_{i=1}^{{{N}_{\text{H}}}}{\sum\limits_{j=1}^{{{N}_{\text{C}}}}{{{\left( {{C}_{2}}Z{{A}^{b}} \right)}_{k,i,j}}+\sum\limits_{i=1}^{{{N}_{\text{H}}}}{{{\left( {{C}_{2}}Z{{A}^{n}} \right)}_{HUi}}}+\sum\limits_{i=1}^{{{N}_{\text{C}}}}{{{\left( {{C}_{2}}Z{{A}^{n}} \right)}_{HUi}},}}}} \\ \end{matrix} $ | (1) |
在优化过程中,本文取每个换热器的换热量Q为优化变量,依据模型中的假设,冷热流股逆流布置.传热计算中,单个换热器满足以下热平衡关系:
| $ {{Q}_{k,i,j}}=GC{{p}_{i}}\left( T_{k,i}^{\text{in}}-T_{k,i}^{\text{out}} \right)=GC{{p}_{i}}\left( T_{k,j}^{\text{out}}-T_{k,j}^{\text{in}} \right), $ | (2) |
| $ {{A}_{k,i,j}}={{Q}_{k,i,j}}{{U}_{i,j}}LMT{{D}_{k,i,j}},k\in {{N}_{\text{K}}},i\in {{N}_{\text{H}}},j\in {{N}_{\text{C}}},\ $ | (3) |
| $ LMT{{D}_{k,i,j}}=\frac{\left( T_{k,i}^{\text{in}}-T_{k,j}^{\text{out}} \right)-\left( T_{k,i}^{\text{out}}-T_{k,j}^{\text{in}} \right)}{\text{Ln}\left[ \left( T_{k,i}^{\text{in}}-T_{k,j}^{\text{out}} \right)/\left( T_{k,i}^{\text{out}}-T_{k,j}^{\text{in}} \right) \right]} $ | (4) |
| $ AMT{{D}_{k,i,j}}=\frac{1}{2}\left[ \left( T_{k,i}^{\text{in}}-T_{k,j}^{\text{out}} \right)+\left( T_{k,i}^{\text{out}}-T_{k,j}^{\text{in}} \right) \right].\ $ | (5) |
在Q为大于0时,则表示此处存在换热器即Z取1,Q等于0时,则表示此处不存在换热器即Z取0,当Q小于0时则加约束惩罚,此外在整个数学模型中,还包括如下约束
单股流体热平衡
| $ \left( TI{{N}_{i}}-TOU{{T}_{i}} \right)GC{{p}_{i}}=\sum\limits_{k=1}^{{{N}_{\text{K}}}}{\sum\limits_{j=1}^{{{N}_{\text{C}}}}{{{Q}_{k,i,j}}+{{Q}_{\text{HU}i}}}},\ \ \ i\in {{N}_{\text{H}}}, $ | (6) |
| $ \left( TOU{{T}_{j}}-TI{{N}_{j}} \right)GC{{p}_{i}}=\sum\limits_{k=1}^{{{N}_{\text{K}}}}{\sum\limits_{i=1}^{{{N}_{\text{C}}}}{{{Q}_{k,i,j}}+{{Q}_{\text{HU}i}}}},\ \ \ j\in {{N}_{\text{C}}},\ $ | (7) |
冷热流股可行出口温度
| $ {{T}_{k,i}}\ge {{T}_{k+1,i}},\ \ \ k\in {{N}_{\text{K}}},\ \ \ i\in {{N}_{\text{H}}},\ $ | (8) |
| $ {{T}_{k,j}}\ge {{T}_{k+1,j}},\ \ \ k\in {{N}_{\text{K}}},\ \ \ j\in {{N}_{\text{C}}}, $ | (9) |
| $ TOU{{T}_{i}}\le T_{i,{{N}_{\text{K}}}}^{\text{out}},\ \ \ i\in {{N}_{\text{H}}}, $ | (10) |
| $ TOU{{T}_{j}}\le T_{j,1}^{\text{out}},\ \ \ j\in {{N}_{\text{C}}}; $ | (11) |
冷热公用工程热平衡
| $ \left( T_{i,{{N}_{\text{K}}}}^{\text{out}}-TOU{{T}_{i}} \right)GC{{p}_{i}}={{Q}_{\text{HU}i}},\ \ i\in {{N}_{\text{H}}}, $ | (12) |
| $ \left( TOU{{T}_{j}}-T_{j,1}^{\text{out}} \right)GC{{p}_{j}}={{Q}_{\text{HU}j}},\ \ j\in {{N}_{\text{C}}}, $ | (13) |
同所有的进化算法一样,DE算法也是对候选解的种群进行操作,利用实数值参数向量作为每一代的种群,DE的中间个体是通过把种群中两个个体之间的加权差向量加到第三个个体上来产生的,这称为“变异”;然后将中间个体的参数与当前个体的参数按照一定规则混合来产生所谓的候选个体,通常称为“交叉”;如果候选个体的目标函数值小于当前个体的目标函数值,候选个体就在下一代中代替当前个体,这一操作称为“选择”.种群中所有个体都要被作为当前个体进行一次变异、交叉和选择操作.本文中,为了解决换热网络问题主要是利用换热网络的分级超结构模型建立并优化换热网络的费用目标函数,优化变量为换热器的换热量Q.
结合换热网络系统优化问题为例,微分进化算法可分为以下几个步骤:
1) 种群初始化:在求解域随机生成初始种群,设置种群规模,本文中优化算例的种群规模为N=10D,D为最大换热器个数.各个优化变量Q在对应的可行域内生成.
2) 变异:
| $ {{v}_{i,g}}\left( j \right)={{Q}_{\min ,}}_{g}\left( j \right)+CF\left( {{Q}_{r1,g}}\left( j \right)-{{Q}_{r2,g}}\left( j \right) \right),\ $ | (14) |
3) 交叉,CR为交叉因子取值(0,1),针对第g代种群个体进行交叉操作.
| $ Q_{i,g}^{'}=\left\{ \begin{matrix} {{v}_{i,g}}\left( j \right),\ \ \ if\ \ CR<P\ \ or\ j=n, \\ {{Q}_{i,g}}\left( j \right),\ \ \ \ otherwise, \\ \end{matrix} \right. $ | (15) |
4) 选择,比较该试验个体与该个体上一代年综合费用,选择较好的个体进入下一代搜索.
| $ {{Q}_{i,g+1}}=\left\{ \begin{matrix} Q_{i,g}^{'},\ \ \ if\ \ F'\left( {{Q}_{i,g}} \right)\le F\left( {{Q}_{i,g}} \right), \\ {{Q}_{i,g}},\ \ \ \ otherwise, \\ \end{matrix} \right. $ | (16) |
在基本DE算法中,种群最优个体是进化的关键,尤其对于换热网络中呈现的严重MINLP问题,最优个体是加快进化速度的关键因素,但是相对应的会带来种群进化早熟的问题,由于变异中的最优个体仅仅是当前种群的最优个体,可能并不是全局最优个体,那么这样的变异机制会导致种群中的其它个体过早的向着种群最优个体的方向变异,减小了种群个体的多样性,而不是去寻找更优的全局最优解,从而很大程度上减弱了算法的全局搜索能力.为解决这一关键问题,本文提出了动态多智能体微分进化算法.
2.2 动态多智能体微分进化算法 2.2.1 多智能体根据文献[12]任何一个能够感知环境并反作用于环境的实体都可看作智能体,而所有由多个自治成分构成的系统都可以表达为一个智能体系统,其特性主要表现为:①每个智能体只有局部感知能力;②没有系统的全局控制;③数据是分散的;④计算是异步的.
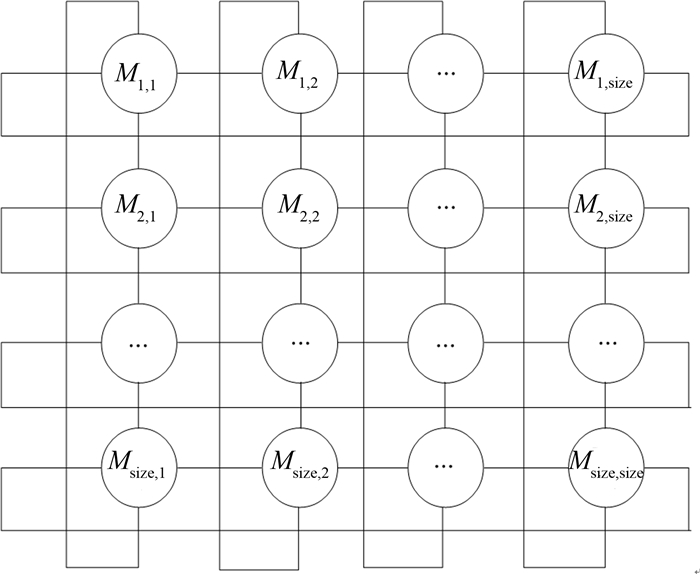
在引入多智能体概念后,一个智能体就表示目标函数的一个解.DE算法在生成初始种群时改为多智能体网格生成机制,所有智能体都被放在一个size×size的网格上,每个智能体占一个格点位置.由于智能体只有局部感知能力,因此它只能与周围智能体发生相互作用,这就构成了如图 2所示的智能体网格.根据图 2,智能体领域概念定义如下:
 |
| 图2 多智能体网格 Fig. 2 Grid of multi-agent |
有智能体Mi,j,i,j=1,2,…,size,其领域为:Mi,jnb{Mi′,j,Mi,j′,Mi″,j,Mi,j″},其中,
| $ \begin{matrix} i'=\left\{ \begin{matrix} i-1,\ \ \ i\ne 1, \\ {{M}_{\operatorname{size}}},\ i=1; \\ \end{matrix}\ \ \ j'=\left\{ \begin{matrix} j-1,\ \ \ j\ne 1, \\ {{M}_{\operatorname{size}}},\ j=1; \\ \end{matrix} \right. \right. \\ i''=\left\{ \begin{matrix} i+1,\ \ i\ne {{M}_{\operatorname{size}}}, \\ 1,\ \ \ i={{M}_{\operatorname{size}}}; \\ \end{matrix}\ \ \ j''=\left\{ \begin{matrix} j+1,\ \ \ j\ne {{M}_{\operatorname{size}}}, \\ 1,\ j={{M}_{\operatorname{size}}}. \\ \end{matrix} \right. \right. \\ \end{matrix} $ | (17) |
每个智能体都有能量,其值为目标函数值的相反数.智能体进化的目标就是尽可能的增大自身的能量,这就导致了智能体间激烈的竞争,但这种竞争智能存在于智能体与其邻域间.最终,能量最低的智能体将死亡,而邻域智能体将占领它的位置.当然合作也可能发生在智能体与其领域间.此外,由于智能体本身也具有智能,它可以利用自身来进行自学习.
邻域竞争算子
主要用来利用邻域的信息来实现智能体间的竞争,邻域进化算子作用在第Mi,j个智能体上,Mmax为Mi,j邻域内能量最大的智能体,若Mi,j比Mmax能量大,则可以继续存活在网格上,否则必须死亡,空出的格点将被Mmax占据.
微分变异算子
不同于标准DE算法,改进算法的微分变异算子为
| $ {{v}_{i,g}}\left( j \right)={{M}_{max,}}\left( j \right)+CF\left( {{Q}_{r1,g}}\left( j \right)-{{Q}_{r2,g}}\left( j \right) \right), $ | (18) |
动态更新的基本思想是对种群中的个体进行动态更新,而不是等所有个体都更新完毕后再以新种群替代旧种群.本文则是利用这种基于动态更新策略改进的微分进化算法.在优化过程中,每一个智能体在变异后,都立即进行一次交叉和选择后生成新的智能体,然后参与当前进化代数中下一个智能体的进化操作.
这种动态更新策略在种群规模不变的情况下更好地加强了种群个体的多样性,以达到增强DE算法的全局搜索能力的目的,同时,由于这种多样性是基于原始种群产生的,所以能较好地保留甚至加强算法本身的鲁棒性.
综上,得到动态多智能体微分进化算法的流程图如图 3.
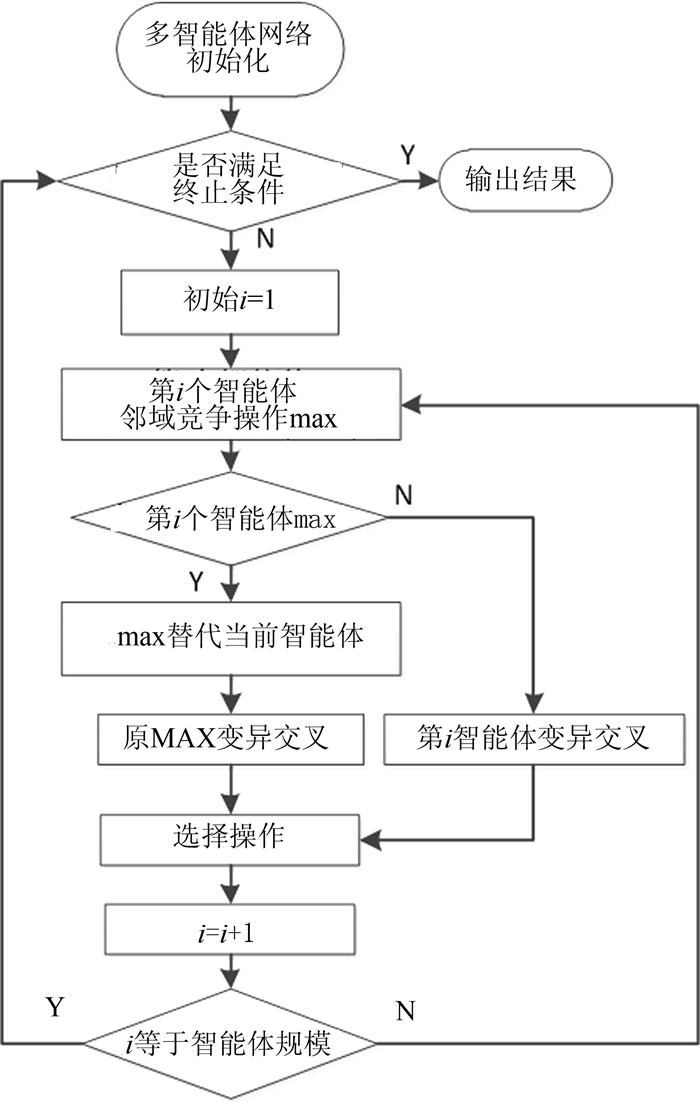 |
| 图3 DMADE算法流程图 Fig. 3 Flow chart of DMADE algorithm program |
采用WIN7环境下Fortran(Compaq Visual Fortran 6)编程,计算机采用Intel(R) Xeon(R) CPU E5-2670 v2 2.5GHz 32GB RAM.
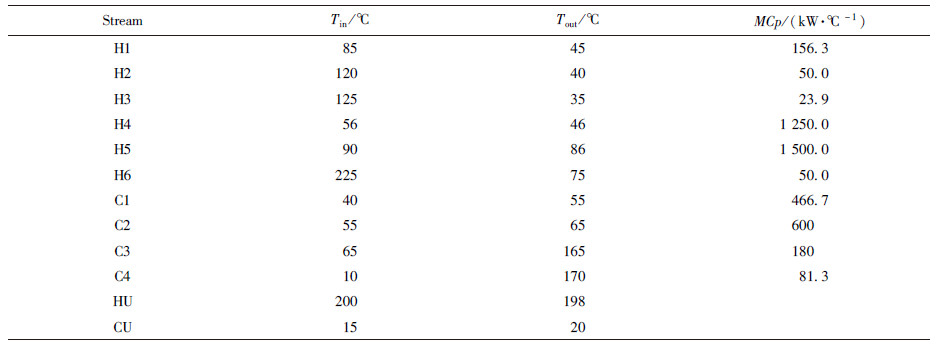
3.1 算例1采用文献[9, 14, 15]的算例,过程流体由6股热流体与4股冷流体组成,冷、热流体及公用工程的初始温度和目标温度、热容流率在表 1中给出.
| 表1 算例1流股参数 Table 1 Stream data in Case 1 |
 |
| 点击放大 |
换热器、冷却器和加热器的传热系数均为K=0.025 kW·(m2·℃)-1,费用计算公式均为60A$·a-1;热公用工程费用为100$·(kW·a)-1;冷公用工程费用为15$·(kW·a)-1.
针对此算例,本文选用3级Grossmann分级超结构模型,则最大换热器个数为NK=3×6×4=72,即目标函数有72维优化变量,分别用动态多智能体微分进化算法与标准微分进化算法优化目标函数求解最小年综合费用.其中,智能体规模size×size=30×30=900,每一个智能体代表一个换热网络结构,对应的年综合投资费用则为智能体的能量,费用越低智能体的能量则越高,为更好地体现算法改进前后的差异,标准微分进化算法种群规模同样取D=900,两者取相同的变异因子CF=0.5,交叉因子CR=0.1,迭代步数为5 000步.
如图 4所示,在进化初期前1 000步迭代时DMADE算法就体现了明显的优化能力,并很快地找到了更优的优化结果,费用下降曲线明显要低于DE算法.从下降趋势分析,DMADE算法一直保有平稳的下降趋势,并且在优化后期的第4 000步迭代时还出现了一个下降阶梯,进一步表现了DMADE算法后期局部最优解跳出了能力,这是因为智能体在进化过程中由于邻域竞争学习更大程度的保持了其自身的智能,使得整个种群在优化后期仍具有一定的多样性并能跳出局部最优解找到更优的结果.在算法稳定性上,迭代过程中舍入误差与截断误差都能控制在很小的范围内,不至于被累计放大,因此整个程序在计算过程中不会出现震荡与结果溢出的问题,都能有效收敛.
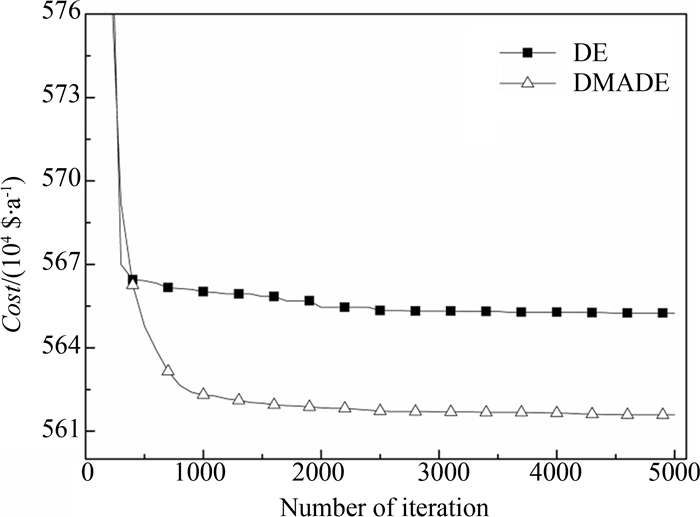 |
| 图4 DE算法与DMADE算法的年综合费用变化对比 Fig. 4 Total annual cost of DE and DMADE |
最终算法收敛得到费用为5 616 298$·a-1,计算时间127.17 s,与其它文献结果相比见表 2,可以看到优化结果有很大的提高.优化得到的换热网络能量分布图见图 5所示(图中数字为换热器的换热量).
| 表2 算例1与文献结果对比 Table 2 Results of Case 1 |
 |
| 点击放大 |
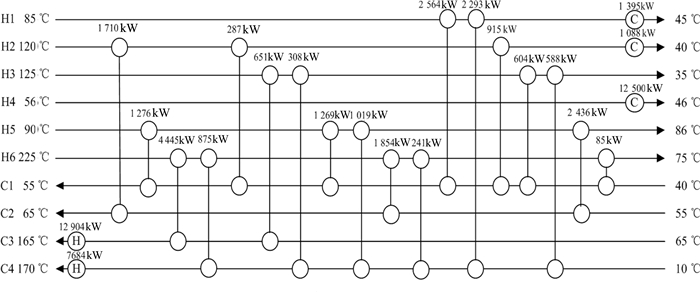 |
| 图5 算例1优化结果 Fig. 5 Result for Case 1 |
采用文献[16, 17]的算例,过程流体由4股热流体和5股冷流体组成.算例的所有初始参数和费用参数同文献[16, 17]完全相同,如表 3所示.换热器费用计算公式2 000+70A[$·(m2·a)-1],热公用工程60$·(kW·a)-1,冷公用工程6$·(kW·a)-1.
| 表3 算例2流股参数 Table 3 Stream data in Case 2 |
 |
| 点击放大 |
针对此算例,本文选用2级Grossmann分级超结构模型,则最大换热器个数为NK=2×4×5=40,即目标函数有40维优化变量.算法中,智能体规模size×size=20×20=400,每一个智能体代表一个换热网络结构,变异因子CF=0.5,交叉因子CR=0.1,最终算法收敛得到费用为2 932 737 $·a-1,计算时间为65.04 s,与其它文献结果相比见表 4,相比文献[17]中改进双层PSO法优化结果有明显的提高.优化得到的换热网络能量分布见图 6.
| 表4 算例2与文献对比结果 Table 4 Results of Case 2 |
 |
| 点击放大 |
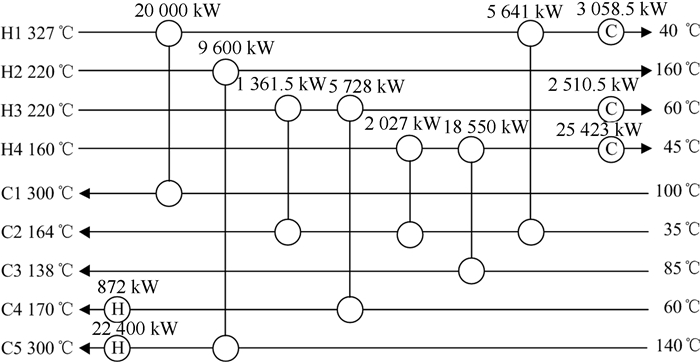 |
| 图6 算例2优化结果 Fig. 6 Result for Case 2 |
利用动态更新策略,将多智能体的优化思想与微分进化算法相结合,改进微分进化算法的变异机制与种群生成机制,并在不增加控制参数的前提下加强种群的多样性,使得算法具有更强的全局搜索能力.对于混合整数非线性的换热网络优化问题,通过工程算例验证,DMADE算法得倒的了更节省的年综合费用结果,优于文献结果,并且重新分配了换热网络的能量分布,使换热网络性能得到很大程度的提升.
| [1] | YI D, HAN Z, WANG K, et al. Strategy for synthesis of flexible heat exchanger networks embedded with system reliability analysis[J]. Chinese Journal of Chemical Engineering (S1004-9541), 2013,21(7):742-753. |
| [2] | LINNHOFF B, HINDMARSH E. The pinch design method for heat exchanger networks[J]. Chemical Engineering Science (S0009-2509), 1983,38(5):745-763. |
| [3] | CERDA J, WESTERBERG A W. Minimum utility usage in heat exchanger network synthesis[J]. Chemical Engineering Science (S0009-2509), 1983,38(3):373-387. |
| [4] | HUANG K F, AL-MUTAIRI E M, KARIMI I A. Heat exchanger network synthesis using a stagewise superstructure with non-isothermal mixing[J]. Chemical Engineering Science (S0009-2509), 2012,73:30-43. |
| [5] | HUO Z, ZHAO L, YIN H, et al. A hybrid swarm intelligence algorithm for simultaneous synthesis of heat exchanger network[J]. CIESC Journal (S0438-1157), 2012,4:20. |
| [6] | STORN R, PRICE K. Differential evolution-A simple and efficient heuristic for global optimization overcontinuous spaces[J]. Journal of Global Optimization (S1573-2916), 1997,11(4):341-359. |
| [7] | WANG Y, LI H X, HUANG T, et al. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting[J]. Applied Soft Computing (S1568-4946), 2014,18:232-247. |
| [8] | BREST J, ZAMUDA A, FISTER I, et al. Large scale global optimization using self-adaptive differential evolution algorithm[C]//2010 IEEE Congress on Evolutionary Computation (CEC), Barcelona, 2010:1-8. |
| [9] | YERRAMSETTY K M, MURTY C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering (S0098-1354), 2008,32(8):1861-1876. |
| [10] | COUELLAN N J, JORQUERA S, GEORGE T. Self-adaptive support vector machine:A multi-agent optimization perspective[J]. Expert Systems with Applications (S0957-4174), 2015,42(9):4284-4298. |
| [11] | CHANG T H, WANG M Y. XF multi-agent distributed optimization via inexact consensus ADMM[J]. LEEE Transactions on Signal Processing (S1053-587X), 2015,63(2):482-497. |
| [12] | 钟伟才,薛明志,刘静,等. 多智能体遗传算法用于超高维函数优化[J]. 自然科学进展, 2003,13(10):1078-1083. |
| [13] | GROSSMANN I E, CABALLERO J A, YEOMANS H. Mathematical programming approachs to the synthesis of chemical process systems[J]. Korean Journal of Chemical Engineering (S0256-1115), 1999,16(4):407-426. |
| [14] | RAVAGNANI M A S S, SILVA A P, ARROYO P A, et al. Heat exchanger network synthesis and optimisation using genetic algorithm[J]. Applied Thermal Engineering (S1359-4311), 2005,25(7):1003-1017. |
| [15] | KHORASANY R F M. A novel approach for synthesis of cost-optimal heat exchanger networks[J]. Computers & Chemical Engineering (S0098-1354), 2008,33(8):1363-1370. |
| [16] | ZHU X X, ONEILL B K, ROACH J R, et al. A method for automated heat exchanger network synthesis using block decomposition and non-linear optimization[J]. Chemical Engineering Research and Design, 1995,73(A8):919-930. |
| [17] | HUO Zhaoyi, ZHAO Liang, YIN Hongchao, et al. Simultaneous synthesis of structural-constrained heat exchanger networks with and without stream splits[J]. The Canadian Journal of Chemical Engineering (S00084034), 2013,91(5):830-842. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
