Barycentric Lagrange Interpolation Collocation Method for Two-dimensional Hyperbolic Telegraph Equation
0 引言
电报方程是一类十分重要的数学物理方程,常被用于刻画化学扩散问题、人口动力系统以及双曲热传导等物理现象,热传导和波传播方程是其特殊情况.双曲型电报方程在电学、弹性力学、流体力学、声学以及微波技术等领域有广泛的应用.另外,在模拟反应扩散问题时,双曲型电报方程比扩散方程更为方便.
近年来,研究工作者提出和发展了多种新型数值方法和格式求解双曲电报方程.针对一维双曲电报方程,已提出和发展了诸如Taylor矩阵法[1]、对偶互易边界积分法[2]、无条件稳定差分格式[3]、修正的B样条配点法[4]、Chebyshev tau法[5]、插值定标法[6]等方法.对一类无界区域上的一维常系数电报方程,齐振民等[7]采用人工边界方法求其数值解.苏令德等[8]基于径向基无网格法分别求解了一、二、三维的线性、非线性电报方程.对于二维双曲电报方程,也得到了许多研究成果.文献[9]中Bülbül等提出Taylor矩阵法,该方法将电报方程转化为矩阵方程求解.文献[10]中Dehghan等分别采用无网格局部强弱式(MLWS)法和无网格局部Petrov-Galerkin(MLPG)法求解了二维双曲电报方程.Dehghan等[11]采用隐式配点法求解了二维双曲电报方程.Jiwari等[12]采用差分积分方法求解了包含狄里克雷和诺依曼边界条件的二维双曲电报方程.
重心Lagrange插值配点法是一种新型的无网格方法,通过采用一些特殊的插值节点分布(如Chebyshev节点)可以得到较高的数值精度和计算稳定性,已被成功应用于求解不同类型的微分方程问题[13].对于与时间相关的初值问题,传统的配点型方法往往在空间域上采用配点格式,而在时间域上采用差分格式.王兆清等[14]提出在空间域和时间域上均采用重心Lagrange插值配点来计算,丰富了该方法的研究领域.但目前重心Lagrange插值配点法仅仅限于求解一维初边值问题.本文给出多变量的重心Lagrange插值公式,提出重心Lagrange插值配点法求解二维双曲电报方程.
1 多变量重心Lagrange插值公式
设函数u(x,y,t)是关于变量x,y,t的函数,其定义域为(x,y,t)∈[a,b]×[c,d]×[0,T].将区间[a,b],[c,d]和[0,T] 分别离散为m,n,l个节点,a=x1<x2<…<xm=b,c=y1<y2<…<yn=d和0=t1<t2<…<tl=T,则在整个定义域上有m×n×l个张量积型插值节点(xi,yj,tk),i=1,…,m;j=1,…,n;k=1,…,l. 利用一维重心Lagrange插值公式,三变量函数的重心Lagrange插值公式可表示为
|
$u\left( {x,y,t} \right) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {{u_{ijk}}{L_i}\left( x \right){M_j}\left( y \right){T_k}\left( t \right),} } } $
|
(1)
|
其中
uijk=
u(
xi,
yj,
tk).
Li(
x)、
Mj(
y)和
Tk(
t)分别是沿
x轴、
y轴和
t轴的重心插值基函数,
|
${L_i}\left( x \right) = {w_i}/\left( {x - {x_i}} \right)/\sum\nolimits_{k = 1}^m {{w_k}/\left( {x - {x_k}} \right),\;\;\;\;i = 1,2,\cdots ,m,} $
|
(2)
|
|
${M_i}\left( y \right) = {v_i}/\left( {y - {y_i}} \right)/\sum\nolimits_{k = 1}^n {{v_k}/\left( {y - {y_k}} \right)} ,\;\;\;\;i = 1,2,\cdots ,n,$
|
(3)
|
|
${T_i}\left( t \right) = {\lambda _i}/\left( {t - {t_i}} \right)/\sum\nolimits_{k = 1}^l {{\lambda _k}/\left( {t - {t_k}} \right),\;\;\;\;i = 1,2,\cdots ,l} .$
|
(4)
|
其中${w_i} = 1/\prod\limits_{i \ne k} {\left( {x - {x_k}} \right)} $,${v_i} = 1/\prod\limits_{i \ne k} {\left( {y - {y_k}} \right)} $,${\lambda _i} = 1/\prod\limits_{i \ne k} {\left( {t - {t_k}} \right)} $.
2 重心Lagrange插值配点法求解电报方程
2.1 问题描述
考虑二维双曲电报方程
|
${u_u}\left( {x,y,t} \right) + 2\alpha {u_t}\left( {x,y,t} \right) + {\beta ^2}u\left( {x,y,t} \right) - f\left( {x,y,t} \right) = {u_{xx}}\left( {x,y,t} \right) + {u_{yy}}\left( {x,y,t} \right),$
|
(5)
|
其中,求解区域
Ω=[0,1]×[0,1]×[
t>0].
u是关于变量
x,y,t的函数,
x,y为空间变量,
t为时间变量.方程(5)中,当
α>0,
β=0时称为阻尼波方程;当
α>0,
β>0时称为电报方程.
初始条件为
|
$u\left( {x,y,0} \right) = {v_1}\left( {x,y} \right),\;\;\left( {x,y} \right) \in \Omega ,$
|
(6)
|
|
$u\left( {x,y,0} \right) = {v_2}\left( {x,y} \right),\;\;\left( {x,y} \right) \in \Omega ;$
|
(7)
|
边界条件为
|
$u\left( {a,y,t} \right) = {h_1}\left( {y,t} \right),\;\;u\left( {x,c,t} \right) = {h_2}\left( {x,t} \right),\;\;\left( {x,,y} \right) \in {\Gamma _u},t > 0,$
|
(8)
|
|
$\frac{{\partial u}}{{\partial x}}\left( {b,y,t} \right) = {g_1}\left( {y,t} \right),\;\;\frac{{\partial u}}{{\partial y}}\left( {x,d,t} \right) = {g_2}\left( {x,t} \right),\;\;\left( {x,y} \right) \in {\Gamma _{\text{q}}},t \geqslant 0,$
|
(9)
|
这里,
Γu、
Γq分别为狄里克雷和诺依曼边界,且
Γu∪
Γq=Γ. Γ为包围区域
Ω的封闭曲线.
2.2 二维双曲电报方程的重心Lagrange插值离散公式
将式(1)直接代入方程(5),可得
|
$\begin{gathered}
\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {\left[{{L_i}\left( x \right){M_j}\left( y \right){{T''}_k}\left( t \right) + 2\alpha {L_i}\left( x \right){M_j}\left( y \right){{T'}_k}\left( t \right) + {\beta ^2}{L_i}\left( x \right){M_j}\left( y \right){T_k}\left( t \right)} \right]{u_{ijk}} - f\left( {x,y,t} \right) = } } } \\
\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {\left[{{{L''}_i}\left( x \right){M_j}\left( y \right){T_k}\left( t \right) + {L_i}\left( x \right){{M''}_j}\left( y \right){T_k}\left( t \right)} \right]{u_{ijk}}.} } } \\
\end{gathered} $
|
(10)
|
令方程(10)在所有节点上均成立,则有
|
$\begin{gathered}
\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {\left[{{L_i}\left( {{x_I}} \right){M_j}\left( {{y_J}} \right){{T''}_k}\left( {{t_K}} \right) + 2\alpha {L_i}\left( {{x_I}} \right){M_j}\left( {{y_J}} \right){{T'}_k}\left( {{t_K}} \right) + {\beta ^2}{L_i}\left( {{x_I}} \right){M_j}\left( {{y_J}} \right){T_k}\left( {{t_K}} \right)} \right]{u_{ijk}} - f\left( {{x_I},{y_J},{t_K}} \right) = } } } \\
\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {\left[{{{L''}_i}\left( {{x_I}} \right){M_j}\left( {{y_J}} \right){T_k}\left( {{t_K}} \right) + {L_i}\left( {{x_I}} \right){{M''}_j}\left( {{y_J}} \right){T_k}\left( {{t_K}} \right)} \right]{u_{ijk}}} } } \\
I = 1,\cdots ,m;\;\;J = 1,\cdots ,n;\;\;K = 1,\cdots ,l. \\
\end{gathered} $
|
(11)
|
令
fijk=
f(
xi,
yj,
tk).注意到
Li(
xI)=
Mi(
xI)=
Ti(
xI)=
δiI,并利用重心Lagrange插值微分矩阵和矩阵张量积
[14]的记号,方程(11)可简写为
|
$\begin{gathered}
\left[{\left( {{T_m} \otimes {I_n}} \right) \otimes {T^{\left( 2 \right)}} + 2\alpha \left( {{I_m} \otimes {I_n}} \right) \otimes {T^{\left( 1 \right)}} + {\beta ^2}\left( {{I_m} \otimes {I_n}} \right) \otimes {I_l}} \right]U - F = \\
\left[{\left( {{L^{\left( 2 \right)}} \otimes {I_n}} \right) \otimes {I_l} + \left( {{I_m} \otimes {M^{\left( 2 \right)}}} \right) \otimes {I_l}} \right]U,\\
\end{gathered} $
|
(12)
|
这里,
L(γ),
M(γ),
T(γ)分别为插值节点
x1,
x2,…,
xm、
y1,
y2,…,
yn和
t1,
t2,…,
tl上的
γ阶微分矩阵,
L(0)=
Im,M(0)=
In,T(0)=
Il,Im,In,Il分别为
m阶、
n阶和
l阶单位矩阵.
U=[
u111,…,
u11n,…,
u1m1,…,
u1mn,…,
ulm1,…,
ulmn]
T,
F=[
f111,…,
f11n,…,
f1m1,…,
f1mn,…,
flm1,…,
flmn]
T.方程(12)可进一步简化为
其中
$$L = \left( {{I_m} \otimes {I_n}} \right) \otimes {T^{\left( 2 \right)}} + 2\alpha \left( {{I_m} \otimes {I_n}} \right) \otimes {T^{\left( 1 \right)}} + {\beta ^2}\left( {{I_m} \otimes {I_n}} \right) \otimes {I_l} - \left( {{L^{\left( 2 \right)}} \otimes {I_n}} \right) \otimes {I_l} - \left( {{I_m} \otimes {M^{\left( 2 \right)}}} \right) \otimes {I_l}.$$
同理,初始条件的离散形式为
|
$\begin{gathered}
u\left( {{x_I},{y_J},0} \right) = {u_{IJ1}} = {v_1}\left( {{x_I},{y_J}} \right),\;\;\;{u_t}\left( {{x_I},{y_J},0} \right) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {{\delta _{iI}}{\delta _{jJ}}T_{1k}^{\left( 1 \right)}{u_{ijk}} = {v_2}\left( {{x_I},{y_J}} \right),} } } \\
I = 1,\cdots ,m;\;\;J = 1,\cdots ,n. \\
\end{gathered} $
|
(14)
|
方程(14)写成矩阵的形式
|
$\left[{\left( {{I_m} \otimes {I_n}} \right) \otimes e_l^1} \right]U = {v_1};\;\;\;\;\;\;\left[{\left( {{I_m} \otimes {I_n}} \right) \otimes T_1^{\left( 1 \right)}} \right]U = {v_2},$
|
(15)
|
这里
el1表示
n阶单位矩阵的第1行;
T(1)1表示关于时间变量的1阶微分矩阵的第1行.
v1=[
v1(
x1,
y1),…,
v1(
x1,
yn),
v1(
x2,
y1),…,
v1(
xm,
yn)]
T;
v2=[
v2(
x1,
y1),…,
v2(
x1,
yn),
v2(
x2,
y1),…,
v2(
xm,
yn)]
T.
边界条件的离散形式为
|
$u\left( {0,{y_J},{t_K}} \right) = {u_{1JK}} = {h_1}\left( {{y_J},{t_K}} \right);\;\;\;\;u\left( {{x_I},0,{t_K}} \right) = {u_{I1K}} = {h_2}\left( {{x_I},{t_K}} \right),$
|
(16)
|
|
$\begin{gathered}
\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {L_{mi}^{\left( 1 \right)}{\delta _{jJ}}{\delta _{kK}} = {g_1}\left( {{y_J},{t_K}} \right);\;\;\;\;\;\;\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^l {{\delta _{iI}}M_{nj}^{\left( 1 \right)}{\delta _{kK}} = {g_2}\left( {{x_I},{t_K}} \right),} } } } } } \\
I = 1,\cdots ,m;\;\;\;\;\;J = 1,\cdots ,n;\;\;\;\;\;\;K = 1,\cdots ,l. \\
\end{gathered} $
|
(17)
|
方程(16)和(17)写成矩阵形式
|
$\begin{array}{*{20}{c}}
{\left[{\left( {e_m^1 \otimes {I_n}} \right) \otimes {I_l}} \right]U = {h_1};}&{\left[{\left( {{I_m} \otimes e_n^1} \right) \otimes {I_l}} \right]U = {h_2},}
\end{array}$
|
(18)
|
|
$\left[{\left( {L_m^{\left( 1 \right)} \otimes {I_n}} \right) \otimes {I_l}} \right]U = {g_1};\;\;\;\;\;\left[{\left( {{I_m} \otimes M_n^{\left( 1 \right)}} \right) \otimes {I_l}} \right]U = {g_2},$
|
(19)
|
这里
h1=[
h1(
y1,
t1),…,
h1(
y1,
tl),
h1(
y2,
t1),…,
h1(
yn,
tl)]
T,
h2=[
h2(
y1,
t1),…,
h2(
y1,
tl),
h2(
y2,
t1),…,
h2(
yn,
tl)]
T,
g1=[
g1(
y1,
t1),…,
g1(
y1,
tl),
g1(
y2,
t1),…,
g1(
yn,
tl)]
T,
g2=[
g2(
x1,
t1),…,
g2(
x1,
tl),
g2(
x2,
t1),…,
g2(
xm,
tl)]
T.
联立求解方程(13)、(15)、(18)和(19),即可求得待求函数u(x,y,t)在各个节点上的函数值.
3 数值算例
重心Lagrange插值配点法的数值精度和计算稳定性依赖特殊的节点分布.本文中,我们采用等距节点和Chebyshev-Gauss-Lobatto节点分布.Chebyshev-Gauss-Lobatto节点分布形式为
|
${x_i} = a + \frac{1}{2}\left( {1 - \cos \frac{{\left( {\left( {i - 1} \right)\pi } \right)}}{{N - 1}}} \right)\left( {b - a} \right),\;\;i = 1,2,\cdots ,N.$
|
(20)
|
为了便于分析方法的计算精度和收敛性,给出5个电报方程的计算算例.所有算例均采用MATLAB编写计算程序,相对误差定义为
|
$\varepsilon = \sqrt {\sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^n {\sum\nolimits_{k = 1}^l {{{\left( {{u_{ijk}} - {{\bar u}_{ijk}}} \right)}^2}/\sum\nolimits_{i = 1}^m {\sum\nolimits_{j = 1}^n {\sum\nolimits_{k = 1}^l {u_{ijk}^2} } } } } } } ,$
|
(21)
|
其中
uijk和${\bar u_{ijk}}$分别为精确解和数值解.另外,为了能和本文方法的数值结果比较,算例1-4选取文献[
10]、算例5选取文献[
12]的相对误差作为参考.文献[
10]中计算参数选取为空间步长Δ
h=0.05,时间步长
τ=0.1.文献[
12]中计算参数选取为空间步长Δ
h=0.05,时间步长
τ=0.001.
算例1 方程(5)中取α=1,β=1,f(x,y,t)=x2+y2+t-2,解析解为u(x,y,t)=x2+y2+t.初始条件为
$$\left\{ \begin{gathered}
u\left( {x,y,0} \right) = {x^2} + {y^2},\;\;0 < x < 1,\;\;0 < y < 1,\hfill \\
{u_t}\left( {x,y,0} \right) = 1\;\;\;\;\;\;\;\;\;\;\;0 < x < 1,\;\;0 < y < 1; \hfill \\
\end{gathered} \right.$$
边界条件
$$\left\{ \begin{gathered}
u\left( {0,y,t} \right) = {t^2} + {y^2},\;\;\;\;0 < y < 1,\;\;\;x = 0,\hfill \\
u\left( {1,y,t} \right) = 1 + t + {y^2}\;\;0 < y < 1,\;\;\;x = 1,\hfill \\
u\left( {x,0,t} \right) = t + {x^2},\;\;\;\;\;0 < x < 1,\;\;\;y = 0,\hfill \\
u\left( {x,1,t} \right) = 1 + t + {x^2},\;0 < x < 1,\;\;\;y = 1. \hfill \\
\end{gathered} \right.$$
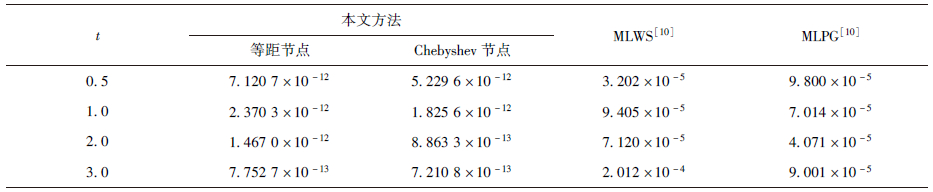
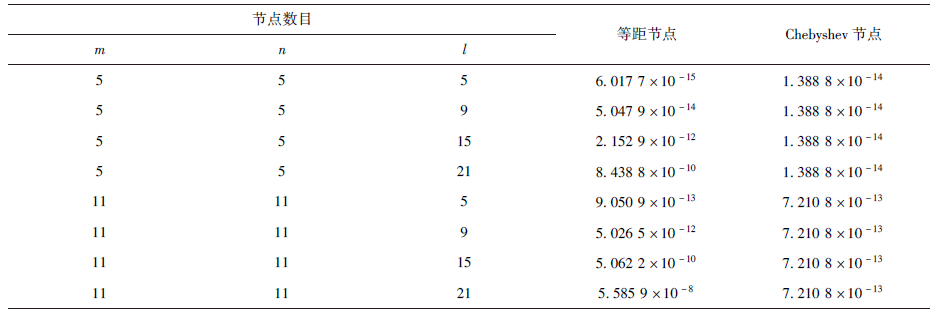
表 1比较了本文方法(节点分布m=n=11,l=7时)与无网格局部强弱式(MLWS)法[10]和无网格局部Petrov-Galerkin(MLPG)法[10]在不同时刻不同节点分布下的相对误差.表 2则给出了时间终值t=3时,本文方法在不同数目等距节点和Chebyshev节点计算条件下的相对误差.表 1表明Chebyshev节点的计算精度要高于等距节点的,且两种节点分布下的相对误差至少比文献[10]中的两种方法小7个数量级.表 2则表明,当节点分布为等距节点时,在时间节点数目固定的情况下,计算误差随空间节点数目的增加而增大;在空间节点数目固定的情况下,计算误差随时间节点数目的增加而增加.在Chebyshev节点分布下,时间方向上的节点分布对计算精度没有任何影响,相对误差随空间节点数目的增加而略有增加,说明在Chebyshev节点分布下,时间方向上采用重心Lagrange插值格式是无条件稳定的.
表1(Table 1)
|
表1 算例1的相对误差
Table 1 Relative errors of Example 1 in numerical schemes at different times
|
表1 算例1的相对误差
Table 1 Relative errors of Example 1 in numerical schemes at different times
| t | 本文方法 | MLWS[10] | MLPG[10] |
| 等距节点 | Chebyshev节点 |
| 0.5 | 7.120 7×10-12 | 5.229 6×10-12 | 3.202×10-5 | 9.800×10-5 |
| 1.0 | 2.370 3×10-12 | 1.825 6×10-12 | 9.405×10-5 | 7.014×10-5 |
| 2.0 | 1.467 0×10-12 | 8.863 3×10-13 | 7.120×10-5 | 4.071×10-5 |
| 3.0 | 7.752 7×10-13 | 7.210 8×10-13 | 2.012×10-4 | 9.001×10-5 |
|
 |
| 点击放大 |
表2(Table 2)
|
表2 算例1 t=3时在不同节点数目下的相对误差
Table 2 Relative errors of Example 1 with different number of nodes at t=3
|
表2 算例1 t=3时在不同节点数目下的相对误差
Table 2 Relative errors of Example 1 with different number of nodes at t=3
| 节点数目 | 等距节点 | Chebyshev节点 |
| m | n | l |
| 5 | 5 | 5 | 6.017 7×10-15 | 1.388 8×10-14 |
| 5 | 5 | 9 | 5.047 9×10-14 | 1.388 8×10-14 |
| 5 | 5 | 15 | 2.152 9×10-12 | 1.388 8×10-14 |
| 5 | 5 | 21 | 8.438 8×10-10 | 1.388 8×10-14 |
| 11 | 11 | 5 | 9.050 9×10-13 | 7.210 8×10-13 |
| 11 | 11 | 9 | 5.026 5×10-12 | 7.210 8×10-13 |
| 11 | 11 | 15 | 5.062 2×10-10 | 7.210 8×10-13 |
| 11 | 11 | 21 | 5.585 9×10-8 | 7.210 8×10-13 |
|
 |
| 点击放大 |
算例2 方程(5)中取α=β=1,f(x,y,t)=2(cost-sint)sinx siny,解析解为u(x,y,t)=cost sinx siny.初始条件为
$$\left\{ \begin{gathered}
u\left( {x,y,0} \right) = \sin x\sin y,\hfill \\
{u_t}\left( {x,y,0} \right) = 0; \hfill \\
\end{gathered} \right.$$
边界条件为
$$\left\{ \begin{gathered}
u\left( {0,y,t} \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x = 0,\;\;\;0 \leqslant y \leqslant 1,\hfill \\
u\left( {1,y,t} \right) = \cos \left( t \right)\sin \left( 1 \right)\sin \left( y \right),\;\;\;\;\;x = 1,\;\;\;0 \leqslant y \leqslant 1,\hfill \\
u\left( {x,0,t} \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y = 0,\;\;\;0 \leqslant x \leqslant 1,\hfill \\
u\left( {x,1,t} \right) = \cos \left( t \right)\sin \left( x \right)\sin \left( 1 \right),\;\;\;\;\;y = 1,\;\;\;0 \leqslant x \leqslant 1. \hfill \\
\end{gathered} \right.$$
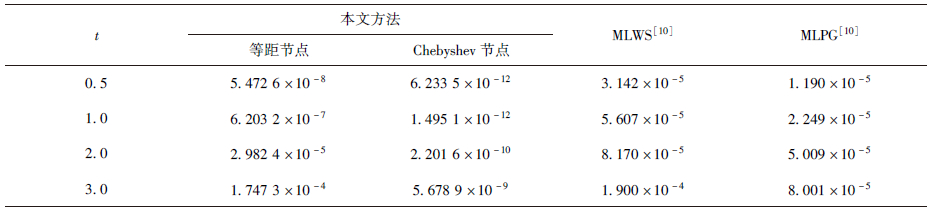
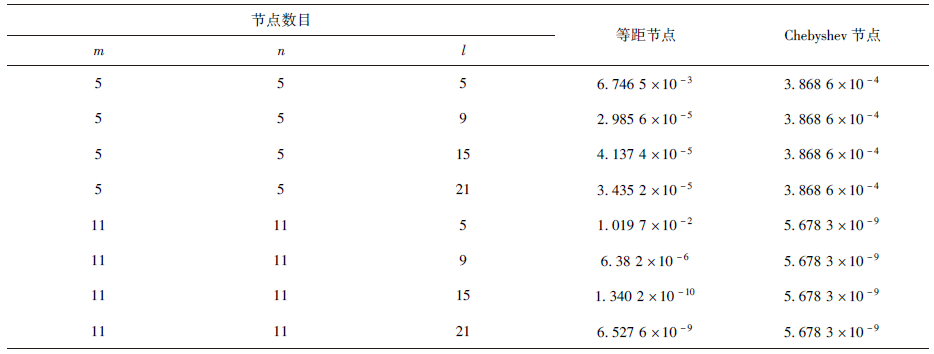
表 3比较了本文方法(节点分布m=n=11,l=7)与MLWS法[10]和MLPG法[10]在不同时刻的相对误差.表 4则给出了时间终值t=3时,本文方法在不同数目等距节点和Chebyshev节点计算条件下的相对误差.从表 3可以看出本文方法的计算效果要优于文献[10]的,尤其是Chebyshev节点分布下的精度非常高.表 4则表明当节点数目增加时,等距节点和Chebyshev节点的相对误差均减小;在Chebyshev节点分布下,时间方向上采用重心Lagrange插值格式是无条件稳定的.
表3(Table 3)
|
表3 算例2的相对误差
Table 3 Relative errors of Example 2 in numerical schemes at different times
|
表3 算例2的相对误差
Table 3 Relative errors of Example 2 in numerical schemes at different times
| t | 本文方法 | MLWS[10] | MLPG[10] |
| 等距节点 | Chebyshev节点 |
| 0.5 | 5.472 6×10-8 | 6.233 5×10-12 | 3.142×10-5 | 1.190×10-5 |
| 1.0 | 6.203 2×10-7 | 1.495 1×10-12 | 5.607×10-5 | 2.249×10-5 |
| 2.0 | 2.982 4×10-5 | 2.201 6×10-10 | 8.170×10-5 | 5.009×10-5 |
| 3.0 | 1.747 3×10-4 | 5.678 9×10-9 | 1.900×10-4 | 8.001×10-5 |
|
 |
| 点击放大 |
表4(Table 4)
|
表4 算例2 t=3时在不同节点数目下的相对误差
Table 4 Relative errors of Example 2 with different number of nodes at t=3
|
表4 算例2 t=3时在不同节点数目下的相对误差
Table 4 Relative errors of Example 2 with different number of nodes at t=3
| 节点数目 | 等距节点 | Chebyshev节点 |
| m | n | l |
| 5 | 5 | 5 | 6.746 5×10-3 | 3.868 6×10-4 |
| 5 | 5 | 9 | 2.985 6×10-5 | 3.868 6×10-4 |
| 5 | 5 | 15 | 4.137 4×10-5 | 3.868 6×10-4 |
| 5 | 5 | 21 | 3.435 2×10-5 | 3.868 6×10-4 |
| 11 | 11 | 5 | 1.019 7×10-2 | 5.678 3×10-9 |
| 11 | 11 | 9 | 6.38 2×10-6 | 5.678 3×10-9 |
| 11 | 11 | 15 | 1.340 2×10-10 | 5.678 3×10-9 |
| 11 | 11 | 21 | 6.527 6×10-9 | 5.678 3×10-9 |
|
 |
| 点击放大 |
算例3 方程(5)中取α=β=1,f(x,y,t)=-2ex+y-t.解析解为u(x,y,t)=ex+y-t.初始条件为
$$\left\{ \begin{gathered}
u\left( {x,y,0} \right) = {{\text{e}}^{\left( {x + y} \right)}},\hfill \\
{u_t}\left( {x,y,0} \right) = - {{\text{e}}^{\left( {x + y} \right)}},\hfill \\
\end{gathered} \right.$$
边界条件为
$$\left\{ \begin{gathered}
u\left( {0,y,t} \right) = {{\text{e}}^{y - t}},\;\;\;\;\;\;\;x = 0,\;\;\;\;\;0 \leqslant y \leqslant 1,\hfill \\
u\left( {1,y,t} \right) = {{\text{e}}^{{\text{1 + y - t}}}},\;\;\;\;\;\;x = 1,\;\;\;\;\;0 \leqslant y \leqslant 1,\hfill \\
\frac{{\partial u}}{{\partial y}}\left( {x,0,t} \right) = {{\text{e}}^{x - t}},\;\;\;\;\;y = 0,\;\;\;\;\;0 \leqslant x \leqslant 1,\hfill \\
u\left( {x,1,t} \right) = {{\text{e}}^{1 + y - t\;}},\;\;\;\;\;y = 1,\;\;\;\;\;0 \leqslant x \leqslant 1,\hfill \\
\end{gathered} \right.$$
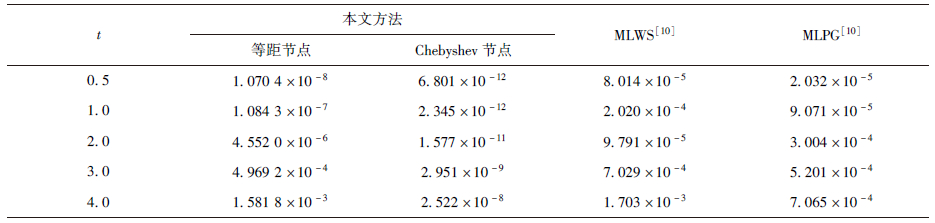
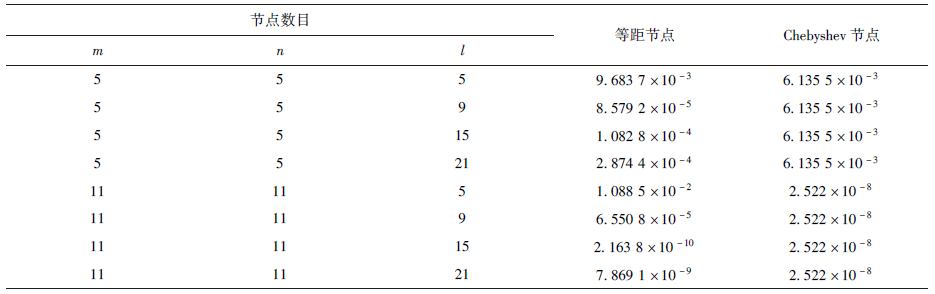
显然,该算例包含Robin边界条件.表 5比较了本文方法(节点分布m=n=11,l=7)与MLWS法[10]和MLPG[10]在不同时刻的相对误差.表 6则给出了时间终值t=4时,本文方法在不同数目等距节点和Chebyshev节点计算条件下的相对误差.从表 5和表 6可以看出,Chebyshev节点分布下,重心Lagrange插值配点法的计算精度要高于等距节点和文献[10]的计算精度,其随空间节点数目的增加而提高,在空间格式上表现出无条件稳定的特点.
表5(Table 5)
|
表5 算例3的相对误差
Table 5 Relative errors of Example 3 in numerical schemes at different times
|
表5 算例3的相对误差
Table 5 Relative errors of Example 3 in numerical schemes at different times
| t | 本文方法 | MLWS[10] | MLPG[10] |
| 等距节点 | Chebyshev节点 |
| 0.5 | 1.070 4×10-8 | 6.801×10-12 | 8.014×10-5 | 2.032×10-5 |
| 1.0 | 1.084 3×10-7 | 2.345×10-12 | 2.020×10-4 | 9.071×10-5 |
| 2.0 | 4.552 0×10-6 | 1.577×10-11 | 9.791×10-5 | 3.004×10-4 |
| 3.0 | 4.969 2×10-4 | 2.951×10-9 | 7.029×10-4 | 5.201×10-4 |
| 4.0 | 1.581 8×10-3 | 2.522×10-8 | 1.703×10-3 | 7.065×10-4 |
|
 |
| 点击放大 |
表6(Table 6)
|
表6 算例3 t=4时在不同节点数目下的相对误差
Table 6 Relative errors of Example 3 with different number of nodes at t=4
|
表6 算例3 t=4时在不同节点数目下的相对误差
Table 6 Relative errors of Example 3 with different number of nodes at t=4
| 节点数目 | 等距节点 | Chebyshev节点 |
| m | n | l |
| 5 | 5 | 5 | 9.683 7×10-3 | 6.135 5×10-3 |
| 5 | 5 | 9 | 8.579 2×10-5 | 6.135 5×10-3 |
| 5 | 5 | 15 | 1.082 8×10-4 | 6.135 5×10-3 |
| 5 | 5 | 21 | 2.874 4×10-4 | 6.135 5×10-3 |
| 11 | 11 | 5 | 1.088 5×10-2 | 2.522×10-8 |
| 11 | 11 | 9 | 6.550 8×10-5 | 2.522×10-8 |
| 11 | 11 | 15 | 2.163 8×10-10 | 2.522×10-8 |
| 11 | 11 | 21 | 7.869 1×10-9 | 2.522×10-8 |
|
 |
| 点击放大 |
算例4 方程(6)中取α=1,β=1,初始条件为
$$\left\{ \begin{gathered}
u\left( {x,y,0} \right) = \sin \left( {\pi x} \right)\sin \left( {\pi y} \right),\hfill \\
{u_t}\left( {x,y,0} \right) = - \sin \left( {\pi x} \right)\sin \left( {\pi y} \right). \hfill \\
\end{gathered} \right.$$
边界条件为
$$\left\{ \begin{gathered}
\frac{{\partial u}}{{\partial x}}\left( {0,y,t} \right) = \pi {{\text{e}}^{ - t}}\sin \left( {\pi y} \right),\;\;\;\;\;x = 0,\;\;\;0 \leqslant y \leqslant 1,\hfill \\
u\left( {1,y,t} \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x = 1,\;\;\;0 \leqslant y \leqslant 1,\hfill \\
u\left( {x,0,t} \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y = 0,\;\;\;0 \leqslant x \leqslant 1,\hfill \\
\frac{{\partial u}}{{\partial y}}\left( {x,1,t} \right) = - \pi {{\text{e}}^{ - t}}\sin \left( {\pi x} \right)\;\;\;\;\;y = 1,\;\;\;0 \leqslant x \leqslant 1. \hfill \\
\end{gathered} \right.$$
该算例包含混合边界条件,其解析解为
u(
x,y,t)=e
-tsin(π
x)sin(π
y).
表 7比较了本文方法(节点分布
m=
n=11,
l=7)与MLWS法
[10]和MLPG法
[10]在不同时刻的相对误差.
表 8则给出了时间终值
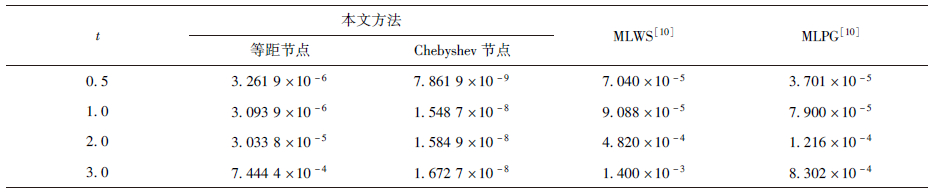
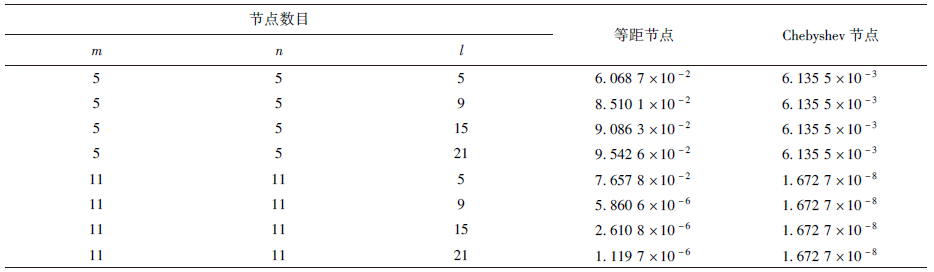
t=3时,本文方法在不同数目等距节点和Chebyshev节点计算条件下的相对误差.从
表 7、
表 8可以看出本文方法在Chebyshev节点分布下具有很高的计算精度.
表7(Table 7)
|
表7 算例4的相对误差
Table 7 Relative errors of Example 4 in numerical schemes at different times
|
表7 算例4的相对误差
Table 7 Relative errors of Example 4 in numerical schemes at different times
| t | 本文方法 | MLWS[10] | MLPG[10] |
| 等距节点 | Chebyshev节点 |
| 0.5 | 3.261 9×10-6 | 7.861 9×10-9 | 7.040×10-5 | 3.701×10-5 |
| 1.0 | 3.093 9×10-6 | 1.548 7×10-8 | 9.088×10-5 | 7.900×10-5 |
| 2.0 | 3.033 8×10-5 | 1.584 9×10-8 | 4.820×10-4 | 1.216×10-4 |
| 3.0 | 7.444 4×10-4 | 1.672 7×10-8 | 1.400×10-3 | 8.302×10-4 |
|
 |
| 点击放大 |
表8(Table 8)
|
表8 算例4 t=3时在不同节点数目下的相对误差
Table 8 Relative errors of Example 4 with different number of nodes at t=3
|
表8 算例4 t=3时在不同节点数目下的相对误差
Table 8 Relative errors of Example 4 with different number of nodes at t=3
| 节点数目 | 等距节点 | Chebyshev节点 |
| m | n | l |
| 5 | 5 | 5 | 6.068 7×10-2 | 6.135 5×10-3 |
| 5 | 5 | 9 | 8.510 1×10-2 | 6.135 5×10-3 |
| 5 | 5 | 15 | 9.086 3×10-2 | 6.135 5×10-3 |
| 5 | 5 | 21 | 9.542 6×10-2 | 6.135 5×10-3 |
| 11 | 11 | 5 | 7.657 8×10-2 | 1.672 7×10-8 |
| 11 | 11 | 9 | 5.860 6×10-6 | 1.672 7×10-8 |
| 11 | 11 | 15 | 2.610 8×10-6 | 1.672 7×10-8 |
| 11 | 11 | 21 | 1.119 7×10-6 | 1.672 7×10-8 |
|
 |
| 点击放大 |
算例5 方程(5)中取α=4π,β2=2π2,解析解为u(x,y,t)=sin(πx)sin(πy)exp[-(x+y)t],f(x,y,t)=2πtsin(π(x+y))exp[π(x+y)t]+[(x+y-2π)2-2t2]sin(πx) sin(πy)exp[-(x+y)t]初始条件为
$$\left\{ \begin{gathered}
u\left( {x,y,0} \right) = \sin \left( {\pi x} \right)\sin \left( {\pi y} \right),\hfill \\
{u_t}\left( {x,y,0} \right) = - \left( {x + y} \right)\sin \left( {\pi x} \right)\sin \left( {\pi y} \right); \hfill \\
\end{gathered} \right.$$
边界条件
$$\left\{ \begin{gathered}
u\left( {0,y,t} \right) = 0,\;\;\;\;\;\;x = 0,\;\;\;0 < y < 1 \hfill \\
u\left( {1,y,t} \right) = 0,\;\;\;\;\;\;x = 1,\;\;\;0 < y < 1,\hfill \\
u\left( {x,0,t} \right) = 0,\;\;\;\;\;y = 0,\;\;\;0 < x < 1,\hfill \\
u\left( {x,1,t} \right) = 0,\;\;\;\;\;y = 1,\;\;\;\;0 < x < 1. \hfill \\
\end{gathered} \right.$$
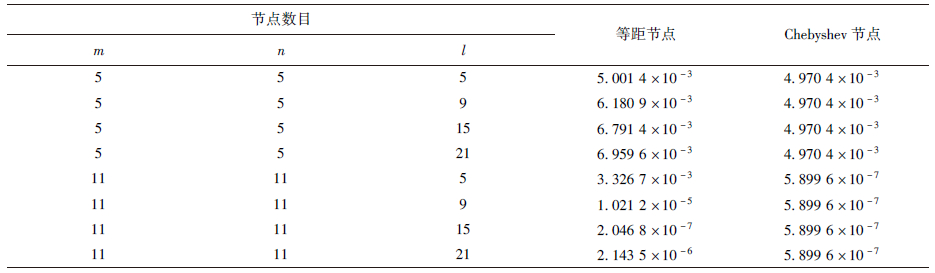
表 9比较了本文方法(节点分布m=n=11,l=7)与文献[12]在不同时刻的相对误差.表 10则给出了时间终值t=3时,本文方法在不同数目等距节点和Chebyshev节点计算条件下的相对误差.从表 9、表 10可以看出,本文方法与解析解吻合的非常好.
表9(Table 9)
|
表9 算例5的相对误差
Table 9 Relative errors of Example 5 in numerical schemes at different times
|
表9 算例5的相对误差
Table 9 Relative errors of Example 5 in numerical schemes at different times
| t | 本文方法 | PDQM[12]
|
| 等距节点 | Chebyshev节点 |
| 0.5 | 3.186 6×10-6 | 2.396 0×10-8 | 3.692 8×10-5 |
| 1.0 | 7.435 7×10-6 | 8.842 2×10-9 | 4.618 9×10-5 |
| 2.0 | 4.876 5×10-5 | 6.450 6×10-8 | 4.201 3×10-5 |
| 3.0 | 1.960 2×10-4 | 5.899 6×10-7 | 3.697 3×10-6 |
|
 |
| 点击放大 |
表10(Table 10)
|
表10 算例5 t=3在不同节点数目下的相对误差
Table 10 Relative errors of Example 5 with different number of nodes at t=3
|
表10 算例5 t=3在不同节点数目下的相对误差
Table 10 Relative errors of Example 5 with different number of nodes at t=3
| 节点数目 | 等距节点 | Chebyshev节点 |
| m | n | l |
| 5 | 5 | 5 | 5.001 4×10-3 | 4.970 4×10-3 |
| 5 | 5 | 9 | 6.180 9×10-3 | 4.970 4×10-3 |
| 5 | 5 | 15 | 6.791 4×10-3 | 4.970 4×10-3 |
| 5 | 5 | 21 | 6.959 6×10-3 | 4.970 4×10-3 |
| 11 | 11 | 5 | 3.326 7×10-3 | 5.899 6×10-7 |
| 11 | 11 | 9 | 1.021 2×10-5 | 5.899 6×10-7 |
| 11 | 11 | 15 | 2.046 8×10-7 | 5.899 6×10-7 |
| 11 | 11 | 21 | 2.143 5×10-6 | 5.899 6×10-7 |
|
 |
| 点击放大 |
4 总结
提出了求解二维双曲电报方程的重心Lagrange插值配点法.采用重心Lagrange插值公式构造了包含时间和空间变量的多变量重心Lagrange插值近似函数.在给定Chebyshev-Gauss-Lobatto节点或等距节点分布上,将多变量重心Lagrange插值近似函数直接代入双曲电报方程及其定解条件,得到系统离散代数方程组.本文方法在时间域和空间域上均采用重心Lagrange插值近似未知函数,可一次性求得全域上所有节点的数值解,可以有效避免差分格式带来的累积误差.几个包含狄里克雷和诺依曼边界条件的数值算例表明:
1) 采用Chebyshev节点的计算精度要高于等距节点的;
2) 采用较少的节点便可获得较高精度的数值结果,且计算精度随节点数目的增加而提高;
3) 计算结果主要依赖空间上的节点分布,在时间上采用重心Lagrange插值格式是无条件稳定的;
4) 理论简单,程序易于实现,非常适合求解三维问题.











 2016, Vol. 33
2016, Vol. 33
