| 基于高阶叠层矢量基函数的E-H时域有限元方法分析谐振腔和波导结构 |
时域数值计算可以通过一次模拟而得到目标的宽频电磁特性,同时可以在时域对非线性介质组成进行精确模拟,因此求解时域麦克斯韦方程成为计算电磁学中必要的组成部分.时域有限差分方法(Finite Difference Time Domain,FDTD)是电磁学领域内被人们广泛、深入地研究,并取得巨大应用成功的时域方法[1, 2, 3].其原理直观、编程简便、易并行、实用性强,但对弯曲表面的阶梯近似严重限制了将其应用于复杂几何结构时的计算精度,很难分析复杂结构的电磁问题.时域有限元方法(Time Domain Finite-Element Method,TDFEM)通过采用非结构网格剖分单元能够方便地对目标的复杂几何结构和介质组成进行精确模拟,有效解决了FDTD方法对于复杂研究对象的建模局限性问题,与FDTD方法相比,有较高的计算精度和较低的色散误差[4, 5, 6, 7].
TDFEM方法通常分为两类,一类是直接离散一阶时域麦克斯韦旋度方程,另一类是离散二阶矢量波动方程[7].大多数情况下研究求解波动方程的TDFEM方法,本文研究基于一阶麦克斯韦旋度方程的TDFEM方法,该方法中电场和磁场作为求解变量,被称为E-H TDFEM方法,不同于另一种直接求解一阶麦克斯韦旋度方程的E-B TDFEM方法[6].与求解波动方程的TDFEM方法相比,E-H TDFEM方法更容易扩展到复杂媒质(色散媒质、各向异性媒质等)的计算;同时,由于E-H TDFEM方法对时间仅展开一阶微分形式,在时间步进过程中只需存储当前时刻和前一时刻的场值,而求解波动方程的TDFEM方法还需存储前前时刻的场值;E-H TDFEM方法中,可采用交替求解电场和磁场的蛙跳格式,更易与FDTD方法混合.
类似于频域中的有限元方法,高阶矢量基函数也用以提高时域有限元方法的计算精度.有两类高阶基函数,一种是插值基函数,另一种是叠层基函数[8, 9, 10, 11, 12].叠层矢量基函数具有叠层特性,即高阶的基函数包含低阶的基函数.在低阶基函数的基础上不断增加新的基函数以构成较高阶的基函数,因此高阶基函数包含了低阶和高阶基函数的特点[7].本文所研究的E-H TDFEM方法中,电场和磁场用相同阶数的叠层矢量基函数展开来提高计算精度,时间离散采用Crank-Nicolson(CN)差分格式使得该方法中时间步长的选取摆脱稳定性条件的限制,同时采用完美匹配层(Perfectly Matched Layers,PML)来截断计算区域,并用以分析三维谐振腔及波导结构.
1方法原理 1.1 叠层矢量基函数基于非结构网格单元的叠层矢量基函数的构成方式详见参考文献[7].这里简要介绍基于四面体网格单元的0.5阶(mixed first-order)以及1.0阶(full first-order)叠层矢量基函数的构成,然后将给出E-H TDFEM方法中所使用的一套基于四面体单元高阶叠层矢量基函数的具体形式.
考虑以下两个与边相关的矢量函数,边的两个顶点分别以i和j表示:${W_{ij}} = {\zeta _i}\nabla {\zeta _j} - {\zeta _j}{\nabla _i},{V_{ij}} = \nabla \left( {{\zeta _i}{\zeta _j}} \right),{\zeta _i}\left( {i = 1,2,3,4} \right)$表示四面体各个顶点的体坐标.Wij和Vij 共同构成了可以用来展开场量(如电场E)的完整的1.0阶(full first-order)基函数.由于$\nabla \times {V_{ij}} = 0,{V_{ij}}$对表示$\nabla \times E$没有任何贡献,此时Vij可以被舍弃以减少基函数的个数,仅保留的Wij构成了0.5阶(mixed first-order)基函数.从全阶数(full order)基函数中舍弃梯度基函数,即舍弃旋度为零的基函数,就构成了混合阶(mixed order)基函数[7].
叠层矢量基函数的组成方式有很多,下面将给出文中E-H TDFEM方法中所采用的一套基于四面体单元的高阶叠层矢量基函数[8, 9, 10, 11],每个基函数表达式后的数字表示该表达式所产生的基函数的个数.由于叠层矢量基函数中,高阶基函数包含了低阶基函数,因此在高阶基函数中只给出增加的基函数.完整的某一阶数的基函数既包含了前面的基函数也包含了增加的基函数.
0.5阶(Mixed first-order)基函数
$${\text{H}}{{\text{2}}^{\text{e}}}:{\zeta _i}\nabla {\zeta _j} - {\zeta _j}\nabla {\zeta _i}\;\;\;\;\left( {i < j} \right),\left( {6个} \right);$$1.0阶(Full first-order)基函数
$${\text{H}}{{\text{2}}^{\text{e}}}:\nabla \left( {{\zeta _i}\;{\zeta _j}} \right)\;\;\;\left( {i < j} \right),\left( {6个} \right);$$1.5阶(Mixed second-order)基函数
$${\text{H}}{{\text{2}}^{\text{f}}}:\begin{array}{*{20}{c}} {{\text{H}}31} \\ {{\text{H}}32} \end{array}\begin{array}{*{20}{c}} {{\zeta _k}\left( {{\zeta _i}\nabla {\zeta _j} - {\zeta _j}\nabla {\zeta _i}} \right),} \\ {{\zeta _j}\left( {{\zeta _k}\nabla {\zeta _i} - {\zeta _i}\nabla {\zeta _k}} \right),} \end{array}\left( {i < j < k} \right),\left( {8个} \right);$$2.0阶(Full second-order)基函数
H4e:$\nabla \left( {{\zeta _i}\zeta _j^2} \right)$ (i<j),(6个);
H5f:$\nabla \left( {{\zeta _i}{\zeta _j}{\zeta _k}} \right)$ (i<j<k),(4个);
2.5阶(Mixed third-order)基函数
$$\begin{gathered} {\text{H}}{{\text{6}}^{\text{f}}}:\left( {{\text{H}}61 - {\text{H}}63} \right)\zeta _k^2\left( {{\zeta _i}\nabla {\zeta _j} - {\zeta _j}\nabla {\zeta _i}} \right)\;\;\;\left( {i \ne j \ne k \ne i} \right),\left( {12{\text{g}}} \right); \\ {\text{H}}71{\zeta _2}{\zeta _3}\left( {{\zeta _1}\nabla {\zeta _4} - {\zeta _4}\nabla {\zeta _1}} \right),\\ {\text{H}}{7^{\text{v}}}:{\text{H}}72{\zeta _2}{\zeta _4}\left( {{\zeta _1}\nabla {z_3} - {\zeta _3}\nabla {\zeta _1}} \right),\left( {3{\text{g}}} \right) \\ {\text{H}}73{\zeta _3}{\zeta _4}\left( {{\zeta _1}\nabla {\zeta _2} - {\zeta _2}\nabla {\zeta _1}} \right),\\ \end{gathered} $$不同于高阶插值矢量基函数,叠层矢量基函数没有统一的表达形式,因此通过编程实现任意阶数叠层矢量基函数的功能并不容易.尽管如此,叠层矢量基函数受到了越来越多的关注,并在有限元方法中实现,在分析电磁问题中发挥越来越大的作用.
1.2 基于叠层矢量基函数的E-H TDFEM方法E-H TDFEM方法从时域麦克斯韦旋度方程出发
| $- \varepsilon \frac{{\partial E}}{{\partial t}} - \sigma E - J + \nabla \times H = 0,$ | (1) |
| $\mu \frac{{\partial H}}{{\partial t}} + {\sigma _{\text{m}}}H + M + \nabla \times E = 0$ | (2) |
用四面体单元剖分区域V,E-H TDFEM方法中,电场和磁场用相同阶数的叠层矢量基函数展开.简化起见,假设区域V为无耗无源区域,测试函数Wi与展开基函数相同,可以得到麦克斯韦方程的伽辽金弱形式
| \[\mathop{{\int\!\!\!\!\!\int\!\!\!\!\!\int}\mkern-31.2mu \bigodot}\limits_V {\left[ {\left( {\varepsilon \frac{{\partial E}}{{\partial t}} - \nabla \times H} \right) \cdot {W_i}} \right]{\text{d}}V = 0,} \] | (3) |
| \[\mathop{{\int\!\!\!\!\!\int\!\!\!\!\!\int}\mkern-31.2mu \bigodot}\limits_V {\left[{\left( {\mu \frac{{\partial E}}{{\partial t}} - \nabla \times H} \right) \cdot {W_i}} \right]{\text{d}}V = 0.} \] | (4) |
| $\left[{M_e^\varepsilon } \right]\frac{{\partial e}}{{\partial t}} - \left[{{S_e}} \right]h = 0,$ | (5) |
| $\left[{M_h^\mu } \right]\frac{{\partial h}}{{\partial t}} - \left[{{S_h}} \right]e = 0,$ | (6) |
同时求解式(5)和(6)可得
| $C\frac{{\partial u}}{{\partial t}} = Du,$ | (7) |
式(7)采用CN差分格式进行时间离散,该差分格式已被广泛的应用于时间偏微分方程中[13],使得时间步长的选取不受稳定性条件的限制而取决于计算精度.采用CN差分,将u=(un+1+un)/2带入式(7)
| $\left( {C - \frac{{\Delta t}}{2}D} \right){u^{n + 1}} = \left( {C + \frac{{\Delta t}}{2}D} \right){u^n},$ | (8) |
这里将采用完美匹配层(PML)吸收边界条件来截断计算区域以模拟开放及半开放问题[14, 15].在PML区域,麦克斯韦方程可以表示为
| $- \varepsilon \bar s*\frac{{\partial E}}{{\partial t}} - \sigma E - J + \nabla \times H = 0,$ | (9) |
| $\mu \bar s*\frac{{\partial H}}{{\partial t}} + {\sigma _m}H + M + \nabla \times E = 0,$ | (10) |
| $\overline{\overline s} = xx\frac{{{S_y}{S_z}}}{{{S_x}}} + yy\frac{{{S_x}{S_z}}}{{{S_y}}} + zz\frac{{{S_x}{S_y}}}{{{S_z}}},$ | (11) |
以z传播方向设置PML吸收边界条件为例,则在PML区域式(8)升级为
| $\left( {C - \frac{{\Delta t}}{2}{D^*}} \right){u^{n + 1}} = \left( {C + \frac{{\Delta t}}{2}{D^*}} \right){u^n} - \Delta tf,$ | (12) |
式(12)为E-H时域有限元方法的最终求解方程,既适用于PML区域也适用于非PML区域,当σz=0时,式(12)等效于适用于自由空间的式(8).
2 数值结果及讨论第一个计算实例是尺寸为1.0 cm×0.5 cm×0.75 cm的无耗矩形谐振腔结构[7],该谐振腔划分为480个四面体.在z=0.25 cm平面上设置正弦调制高斯脉冲作为激励源.
叠层矢量基函数分别取0.5阶、1.0阶、1.5阶和2.0阶时,E-H TDFEM方法计算所得的观察点(0.75 cm,0.25 cm,0.625 cm)处的时域波形如图 1所示.由图中明显看出,0.5阶基函数计算所得的时域波形图与1.0阶、1.5阶和2.0阶基函数计算所得的波形图差别较大,而1.5阶和2.0阶基函数计算所得的波形图吻合最好.将观察点处的时域波形做FFT变换并归一化,归一化后所得频谱图的峰值所对应频率点的值即表示谐振腔的不同谐振频率点,其中,最小的谐振频率点即是最低谐振频率[16].表 1所示为基函数分别取0.5阶、1.0阶、1.5阶和2.0阶时,E-H TDFEM方法计算所得的该谐振腔最低谐振频率与解析解[7]的比较.图 1中的现象在表 1中也可以看到,0.5阶基函数计算所得的值误差最大,为4.12%;1.5阶和2.0阶基函数计算所得的值的误差都为0.09%,低于1.0阶基函数计算所得的值的误差0.64%.显然,相同的网格剖分情况下,高阶叠层矢量基函数的使用可以提高E-H TDFEM方法的计算精度.与2.0阶基函数相比,1.5阶基函数在保持相同计算精度的同时可以减少叠层矢量基函数的总个数.
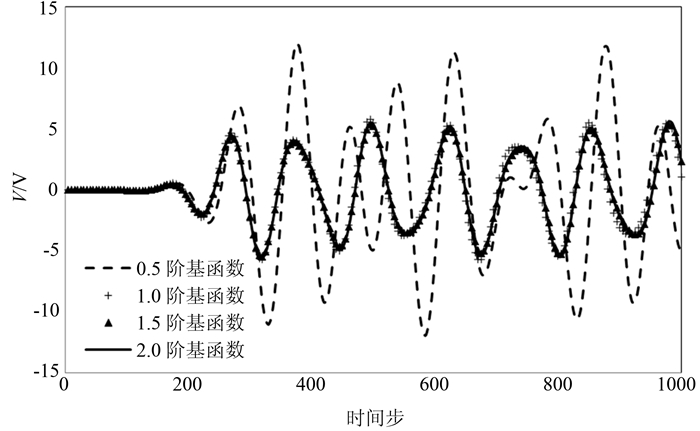 |
| 图1 基函数分别取0.5阶、1.0阶、1.5阶和2.0阶时,E-H TDFEM方法计算所得的观察点处的时域波形 Fig. 1 Time-domain waveforms at observation point obtained by E-H TDFEM with mixed and full first-order, second-order hierarchical vector basis functions |
| 表1 基函数分别取0.5阶、1.0阶、1.5阶和2.0阶时,E-H TDFEM方法计算所得的谐振频率与解析解的比较 Table 1 First resonant frequency of rectangular cavity obtained by E-H TDFEM with mixed and full first-order, second-order hierarchical vector basis functions, compared with analytical result |
 |
| 点击放大 |
第二个例子是尺寸为1.5 mm×0.5 mm×1.0 mm的高谐振频率无耗矩形谐振腔结构[17].将该谐振腔划分为120个四面体单元.同样的,将正弦调制高斯脉冲作为激励源.叠层矢量基函数分别取0.5阶、1.5阶和2.5阶时,E-H TDFEM方法计算所得的观察点处的时域波形如图 2所示.由图中明显看出,0.5阶基函数计算所得的时域波形图与1.5阶和2.5阶基函数计算所得的波形图差别较大,后两者吻合很好.
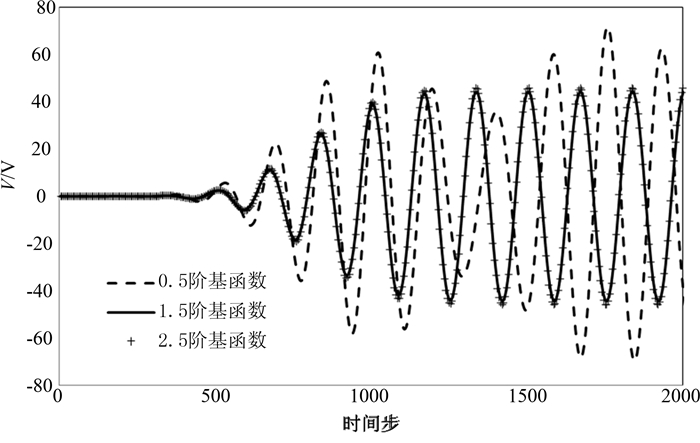 |
| 图2 基函数分别取0.5阶、1.5阶和2.5阶时,E-H TDFEM方法计算所得的观察点处的时域波形 Fig. 2 Time-domain waveforms at observation point obtained by E-H TDFEM with mixed first-order, second-order and third-order hierarchical vector basis functions |
表 2所示为当基函数分别取0.5阶、1.0阶、1.5阶和2.5阶时,E-H TDFEM方法计算所得的该谐振腔的谐振频率与解析解[17]的比较.当基函数取0.5阶时,无法得到满意的解;当基函数取1.5阶和2.5阶时,计算误差均为0.02%,低于1.0阶基函数计算所得的值的误差1.03%.显然,相同的网格剖分情况下,高阶叠层矢量基函数的使用可以提高E-H TDFEM方法的计算精度.与2.5阶基函数相比,1.5阶基函数在保持相同计算精度的同时可以减少基函数的个数.
| 表2 基函数分别取0.5阶、1.0阶、1.5阶和2.5阶时,E-H TDFEM方法计算所得的谐振频率与解析解的比较 Table 2 Resonant frequency of cavity obtained by E-H TDFEM with mixed first-order, second-order and third-order hierarchical vector basis functions, compared with analytical result |
 |
| 点击放大 |
为了提高计算精度的两种途径,一是加密网格,二是提高基函数的阶数,图 3将这两种途径进行了比较.图 3中实线表示当网格单元数为120个四面体单元时,各阶E-H TDFEM方法计算所得的谐振频率误差曲线,当基函数取1.0阶时,加密网格至3 750个四面体单元,计算误差为0.18%.由图中可以看出随着网格的加密,数值精度的提高缓慢,高阶基函数能用较少的未知量获得更高的精度.因此提高基函数的阶数能够比加密网格更快地达到所需要的计算精度.
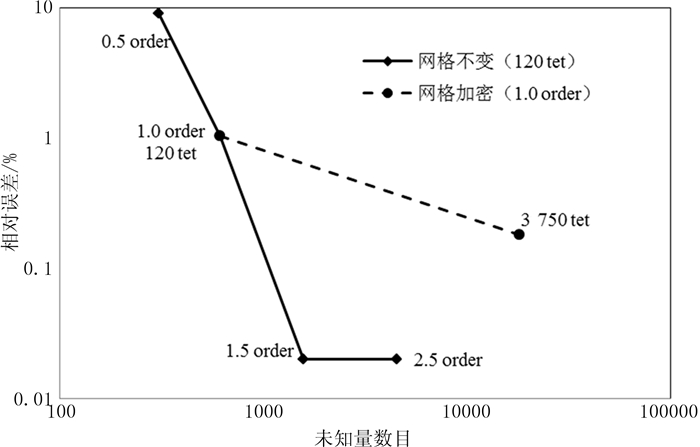 |
| 图3 各阶E-H TDFEM方法计算所得的谐振频率误差曲线 Fig. 3 Relative errors of resonant frequency obtained by E-H TDFEM with different order of hierarchical vector basis functions under different number of meshes |
第三个例子是部分填充的全高介质矩形波导结构[18],如图 4所示.波导宽a=22.86 mm,高b=10.16 mm,介电常数εr=8.2,填充介质宽w=12 mm,长L=6 mm.中心频率为10 GHz的高斯调制脉冲作为激励源.结构两端由PML截断,最外层是金属壁,整个计算区域剖分为2 880个四面体.
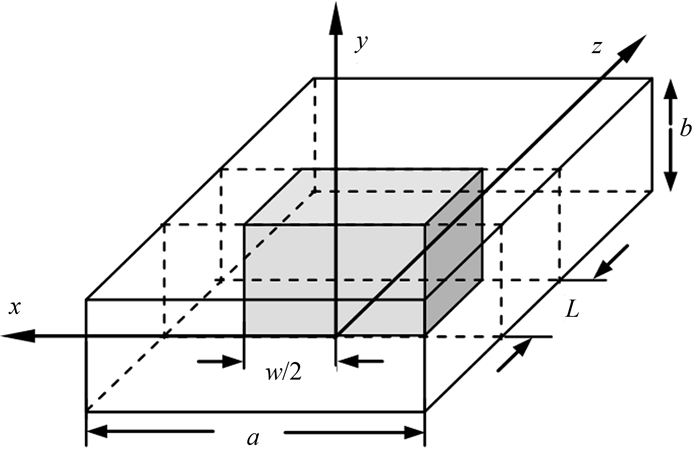 |
| 图4 部分填充的全高介质矩形波导 Fig. 4 Configuration of a partially dielectric-filled rectangular waveguide |
当基函数取0.5阶和1.5阶时,E-H TDFEM方法计算所得的空波导观察点处的时域波形比较图如图 5所示.很显然,1.5阶基函数计算所得的波形图与激励源吻合很好,同时也显示出PML良好的吸收效果,而0.5阶基函数计算无法得到满意的波形图.结果表明,在相同的网格剖分情况下,电场和磁场用1.5阶基函数展开与用0.5阶基函数展开相比可以获得更高的精度.由采用1.5阶基函数的E-H TDFEM方法计算所得的该波导结构的S11参数图如图 6所示,并与基于二阶矢量波动方程的TDFEM方法及频域FEM方法所得到的计算结果进行比较,可以看出三者吻合很好.
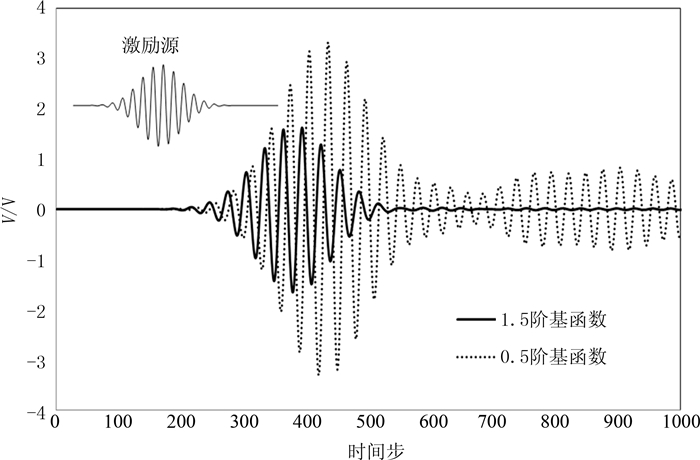 |
| 图5 基函数取0.5阶和1.5阶时,观察点处的时域波形 Fig. 5 Time-domain waveforms at observation point obtained by E-H TDFEM with mixed first-order and mixed second-order hierarchical vector basis functions |
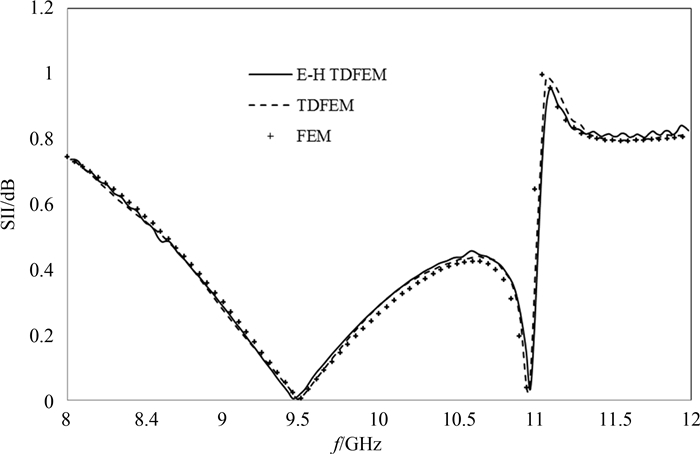 |
| 图6 由高阶E-H TDFEM、基于二阶矢量波动方程的TDFEM方法及频域FEM方法计算所得到的全高介质波导的S11参数 Fig. 6 S11 parameters of dielectric-filled rectangular waveguide obtained by hierarchical E-H TDFEM and by vector wave equation based TDFEM and FEM |
将一套基于四面体网格单元的高阶叠层矢量基函数应用于E-H时域有限元方法中来分析三维谐振腔和部分介质填充的波导问题.该方法中,电场和磁场用相同阶数的叠层矢量基函数展开并同时求解,时间离散采用CN差分格式使得时间步长的选取不受稳定性条件的限制而取决于计算精度,同时采用PML吸收边界条件来截断计算区域.计算结果表明,在相同的网格剖分情况下,相较于低阶基函数,高阶叠层矢量基函数的使用可以有效提高E-H时域有限元方法的计算精度;在满足相同计算精度的情况下,可采用较低阶的基函数来减少叠层矢量基函数的个数,提高计算效率.
| [1] | YEE K S. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Trans Antennas Propagat, 1966, 14:302-307. |
| [2] | ZHOU H, LIU Y, LI H, et al. Computational electromagnetic and applications in numerical simulation of electromagnetic environment effects and development tendency[J].Chinese J Comput Phys, 2014, 31(4):379-389. |
| [3] | KUANG X, WANG D, ZHANG L, et al. Finite difference time-domain method based on high order compact scheme[J]. Chinese J Comput Phys, 2014, 31(1):91-95. |
| [4] | LEE J F. WETD-a finite element time-domain approach for solving Maxwell's equations[J]. IEEE Microwave and Guided Wave Letters, 1994, 4:11-13. |
| [5] | GEDNEY S D, NAVSARIWALA U. An unconditionally stable finite element time-domain solution of the vector wave equation[J]. IEEE Microwave and Guided Wave Letters, 1995, 5:332-334. |
| [6] | DONDERICI B, TEIXEIRA F L. Mixed finite-element time-domain method for transient Maxwell equations in doubly dispersive media[J]. IEEE Trans Microwave Theory Tech, 2008, 56(1):113-120. |
| [7] | JIN J M. The finite element method in electromagnetics[M]. 3rd ed. New York:Wiley, 2014. |
| [8] | WEBB J P, FORGHANI B. Hierarchal scalar and vector tetrahedral[J]. IEEE Trans Magn, 1993, 29:1495-1498. |
| [9] | ANDERSEN L S, VOLAKIS J L. Hierarchical tangential vector finite elements for tetrahedral[J]. IEEE Microwave Guided Wave Lett, 1998, 8:127-129. |
| [10] | SAVAGE J S, PETERSON A F. Higher-order vector finite elements for tetrahedral cells[J]. IEEE Trans Microwave Theory Tech, 1996, 44:874-879. |
| [11] | WEBB J P. Hierarchal vector basis functions of arbitrary order for triangular and tetrahedral finite elements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(8):1244-1253. |
| [12] | ZHU Y, CANGELLARIS A. Multigrid finite element methods for electromagnetic field modeling[M]. Hoboken, NJ:Wiley-IEEE, 2006. |
| [13] | YANG Y, CHEN R S,WANG D X, YUNG E K N. Unconditionally stable Crank-Nicolson finite-difference time-domain method for simulation of 3-D microwave circuits[J]. IET Microw Antennas Propag, 2007, 1(4):937-942. |
| [14] | GEDNEY S D. An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(12):1630-1639. |
| [15] | JIAO D, JIN J M, MICHIELSSEN E, et al. Time-domain finite-element simulation of three-dimensional scattering and radiation problems using perfectly matched layers[J]. IEEE Transactions on Antennas and Propagatiion, 2003,51(2):296-305. |
| [16] | JN W P Carpes, PICHON L, RAZEK A. Efficient analysis of resonant cavities by finite element method in the time domain[J]. IEE Proc-Microw Antennas Propagation, 2000, 147(1):53-56. |
| [17] | MOVAHHEDI M, ABDIPOUR A. Alternation-direction implicit formulation of the finite-element time-domain method[J]. IEEE Trans Microwave Theory Tech, 2007, 55:1322-1331. |
| [18] | CHEN R S, YUNG E K N, CHAN C H, WANG D X, FANG D G. Application of the SSOR preconditioned CG algorithm to the vector FEM for 3-D full-wave analysis of electromagnetic-field boundary-value problems[J]. IEEE Trans Microwave Theory Tech, 2002, 50(4):1165-1172. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

