中国石油勘探开发研究院, 北京 海淀 100083
Pressure Dynamic Analysis of Vertical Well Flow with Partial Penetration Fractures
Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
0 引言
低渗透碳酸盐岩储层具有储层厚度大、天然裂缝发育等特点,一般采用射孔完井和水力压裂增产,但是射开范围比较小,一般只有几米,造成了生产井的不完善性.因此,研究该类型储层部分射开压裂直井的渗流压力意义重大.
国外学者对于均质(非均质)油藏部分(完全)射开问题做了很多研究,且取得了很大进展.1963年Warren研究了均质油藏完全射开直井渗流压力表达式[1];1969年Mills和Clegg分析了非均质油藏直井不稳定渗流压力分布[2];1973年Ramey和Gringarten利用格林函数方法给出了部分射开直井裂缝的压力解析解[3, 4];1980年Buhidmal利用格林函数方法给出了定压边界和封闭边界条件下的渗流压力解析表达式[5];1987年Kucuk对部分射开直井的渗流压力动态特征进行了分析[6];1990年Hegeman和Abbaszaden给出了无限大油藏部分射开大斜度井的渗流压力解[7];1991年Raghavan和Ozkan求解出了无限大油藏部分射开直井渗流压力点源解[8];1993年Onur给出了具有天然裂缝的均质油藏完全射开直井解析解[9];2000年Bui给出了双重介质均质油藏部分射开直井渗流压力点源解[10].
国内学者也做过一些研究,如冯文光和葛家理对于单一介质、双重介质中的低速非达西渗流和压力曲线动态特征做了详细的研究,并绘制了压力动态特征曲线图版[11, 12];同登科、李凡华等人给出了含有启动压力梯度的不稳定渗流压力表达式[13, 14];程时清、宋付权等人利用分离变量方法给出了渗流压力近似解[15, 16];刘启国、刘青山等人利用边界元方法来分析复杂油藏不稳定渗流问题[17, 18];王建平等人给出了各向异性部分射开直井渗流压力拉氏空间解析解[19].大部分方法都是基于Gringarten and Ramey[3]的点源解和格林函数方法,来解决不同类型储层流体渗流压力问题.但是最初Gringarten and Ramey[3]建立的物理模型只考虑了上下边界封闭,适用性不强.
本文首先建立非均质油藏部分射开物理模型,然后通过假定条件,建立三维各向异性矩形油藏的不稳定渗流数学模型,考虑不渗透顶、底边界和定压顶、底边界等不同边界条件组合的情况,通过无因次量纲变换、拉普拉斯变换、傅里叶余弦变换和分离变量等数学方法,求解不稳定渗流数学模型在拉普拉斯实数域的解析解,利用斯蒂芬森数值反演方法,得出实数域的压力数值解,并绘制压力动态曲线,研究部分射开压裂直井的试井分析问题.
1 部分射开压裂直井渗流模型
1.1 物理模型描述
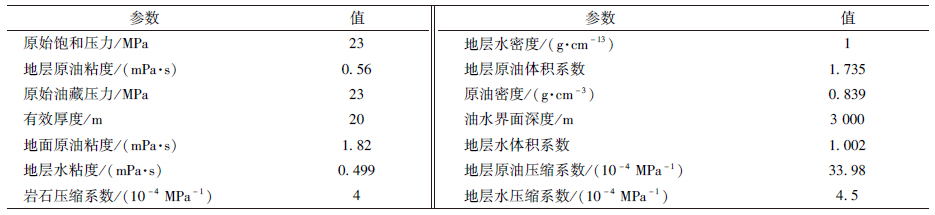
储层经过水力压裂,形成如图 1所示的多条裂缝的直井,其中,裂缝半长和裂缝高度构成了压裂缝面,与裂缝间距半长构成了储层流体一维扩散范围,扩散范围影响储层流体在纵向上的流量大小;裂缝缝宽及缝面构成了裂缝中流体达西流动的作用范围,影响整个直井产量,可根据储层-裂缝-井筒的耦合模型分析压裂参数对分段压裂直井渗流压力的影响,分析敏感性因素,找出最大产量的人工裂缝参数组合,形成最优裂缝网格,达到产量优化的目的.因此为研究压裂直井的渗流压力,首先研究单裂缝渗流压力,如图 2所示,然后利用叠加原理,求得多裂缝渗流压力,将物理模型进行简化,并做如下假设:
1) 生产井定产量生产,地层为等厚、有界、非均质油藏;
2) 生产井生产前,储层压力各处相等,均等于原始地层压力;
3) 储层流体微可压缩,发生单相不稳定渗流;
4) 忽略压开各条裂缝间干扰,流体在裂缝中的流动遵循达西定律;
5) 不计重力、毛管力的影响,孔隙度、流体黏度视为常数;
6) 储层不完全射开,储层流体在有限范围内流向井筒;
7) 不考虑流体在基质中的渗流和裂缝与基质间的窜流,裂缝具有无限导流能力.
1.2 数学模型
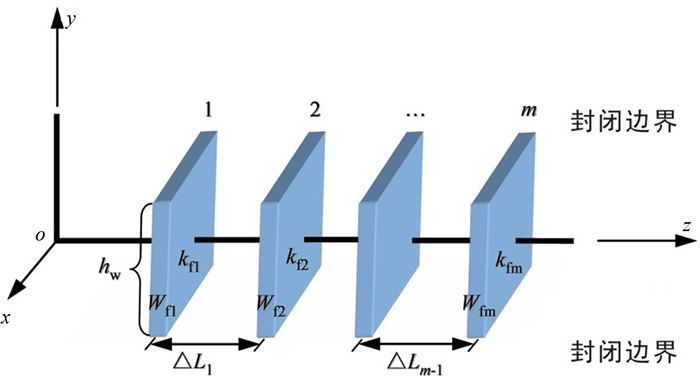
某一单一裂缝中心位于(x0,y0,z0)处,基于上述假设,对该裂缝建立如下数学模型
|
$\frac{{{k_x}}}{{\phi \mu {c_{\rm{t}}}}}\frac{{{\partial ^2}P}}{{\partial {x^2}}} + \frac{{{k_y}}}{{\phi \mu {c_{\rm{t}}}}}\frac{{{\partial ^2}P}}{{\partial {y^2}}} + \frac{{{k_z}}}{{\phi \mu {c_{\rm{t}}}}}\frac{{{\partial ^2}P}}{{\partial {z^2}}} + \frac{{8q{w_x}{w_y}{w_z}}}{{\phi \mu {c_{\rm{t}}}}}f\left( {x,y,z} \right) = \frac{{\partial P}}{{\partial t}},$
|
(1)
|
式中,
kx、ky、kz为
x、y、z方向上的渗透率,mD;
ϕ为孔隙度,小数;
ct为综合压缩系数,MPa·m
-1;
t为生产时间,d;
p为储层压力,MPa;
B为储层压力下的体积系数,m
3·m
-3;
μ为流体黏度,mPa·s;
q 为单位面积流过裂缝的的流量,m
2·d
-1.
f(
x,y,z)为源(汇)相的位置
|
$f\left( {x,y,z} \right) = \frac{1}{{8{w_x}{w_y}{w_z}}}\iiint\limits_v {\delta \left[{\left( {x - {x_0}} \right)\left( {y - {y_0}} \right)\left( {z - {z_0}} \right)} \right]{\text{d}}v},$
|
(2)
|
|
$\left( {{x_0} - {w_x}} \right)\left( {{y_0} - {w_y}} \right)\left( {{z_{00}} - {w_z}} \right) \leqslant v \leqslant \left( {{x_0} + {w_x}} \right)\left( {{y_0} + {w_y}} \right)\left( {{z_0} + {w_z}} \right),$
|
(3)
|
式中:
δ为Dirac Delta函数.
初始条件为
|
$p\left( {x,y,z,0} \right) = {p_i};$
|
(4)
|
内边界条件为
|
$\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{r \to {r_{\text{w}}}} \left( {r\frac{{\partial p}}{{\partial r}}} \right) = \frac{{Bq\mu }}{{2\pi kh}},}&{r = \sqrt {{{\left( {x - {x_0}} \right)}^2} + {{\left( {x - {x_0}} \right)}^2} + {{\left( {x - {x_0}} \right)}^2}} ;}
\end{array}$
|
(5)
|
外边界条件为
|
$\begin{array}{*{20}{c}}
{\frac{{\partial p}}{{\partial x}}\left| {_{x = 0,a} = 0,} \right.}&{\frac{{\partial p}}{{\partial y}}\left| {{y_{x = 0,b}} = 0,} \right.}&{\frac{{\partial p}}{{\partial z}}\left| {_{z = 0,h} = 0.} \right.}
\end{array}$
|
(6)
|
2 模型求解
2.1 解法
求解部分射开直井渗流压力数学模型主要有三种方法:忽略压力传播时间,采用格林函数方法,求得模型的拉氏空间解析解[11, 12, 20];将边界扩展视为时间的函数,运用稳态逐次替换方法和差分离散化方法,求得模型的数值解[14];利用数值逼近方法和级数思想,来研究部分射开直井渗流压力传播前缘与时间的相关问题[21].本文通过无因次量纲变换、拉普拉斯变换、傅里叶余弦变换和分离变量法等数学方法,对式(1)进行求解.
2.2 无因次量纲化
无因次量纲化是一种把渗流方程转化为常规数学方程的方法.通过无量纲化,可大大减少计算对比次数,使得数学物理方程变得简洁、整齐,便于分析和求解,有助于渗流方程的检查和验证[22].引入以下无因次量
|
$N = \sqrt {abh/L} ,$
|
(7)
|
|
$\begin{array}{*{20}{c}}
{{P_D} = \frac{{2\pi kN\left( {{p_i} - p} \right)}}{{QB\mu }}}&{{t_D} = \frac{k}{{\phi \mu {c_{\text{t}}}{N^2}}}t,}
\end{array}$
|
(8)
|
|
$\begin{array}{*{20}{c}}
{{x_{\text{D}}} = \sqrt {k/{k_x}} x/N,}&{{y_D} = \sqrt {k/{k_x}} y/N,}&{{z_{\text{D}}} = \sqrt {k/{k_x}} z/N,}
\end{array}$
|
(9)
|
|
$\begin{array}{*{20}{c}}
{{a_{\text{D}}} = a/N,}&{{b_{\text{D}}} = b/N,}&{{h_{\text{D}}} = h/N}
\end{array},$
|
(10)
|
|
$\begin{array}{*{20}{c}}
{{w_{x{\text{D}}}} = {w_x}/N,}&{{w_{y{\text{D}}}} = {w_y}{w_{x{\text{D}}}} = {w_x}/N,}&{{w_{z{\text{D}}}} = {w_z}/N,}
\end{array}$
|
(11)
|
|
$\begin{array}{*{20}{c}}
{{x_{0{\text{D}}}} = {x_0}/r,}&{{y_{0{\text{D}}}} = {y_0}/r}&{{z_{0{\text{D}}}} = {z_0}/r,}
\end{array}$
|
(12)
|
式中,
L为射开储层长度,m. 式(1)无因次量纲化后得
|
$\frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial x_{\text{D}}^2}} + \frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial y_{\text{D}}^2}} + \frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial z_{\text{D}}^2}} + \frac{{4\pi }}{{{N^2}}}f\left( {{x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}}} \right){\text{ = }}\frac{{\partial {P_{\text{D}}}}}{{\partial {t_{\text{D}}}}},$
|
(13)
|
式中
|
$f\left( {{x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}}} \right) = \frac{1}{{8{w_{x{\text{D}}}}{w_{y{\text{D}}}}{w_{z{\text{D}}}}}}\iiint\limits_{{v_{\text{D}}}} {\delta \left[{\left( {{x_{\text{D}}} - {x_{0{\text{D}}}}} \right)\left( {{y_{\text{D}}} - {y_{0{\text{D}}}}} \right)\left( {{z_{\text{D}}} - {z_{0{\text{D}}}}} \right)} \right]{\text{d}}{v_{\text{D}}},}$
|
(14)
|
|
$\left( {{x_{0{\text{D}}}} - {w_{x{\text{D}}}}} \right)\left( {{y_{0{\text{D}}}} - {w_{y{\text{D}}}}} \right)\left( {{z_{0{\text{D}}}} - {w_{z{\text{D}}}}} \right) \leqslant {v_{\text{D}}} \leqslant \left( {{x_{0{\text{D}}}} + {w_{x{\text{D}}}}} \right)\left( {{y_{0{\text{D}}}} + {w_{y{\text{D}}}}} \right)\left( {{z_{0{\text{D}}}} + {w_{z{\text{D}}}}} \right),$
|
(15)
|
初始条件为
|
${p_{\text{D}}}\left( {{x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}},0} \right) = 0;$
|
(16)
|
内边界条件为
|
$\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{{r_{\text{D}}} \to 1} \left( {{r_{\text{D}}}\frac{{\partial {p_{\text{D}}}}}{{\partial {r_D}}}} \right) = - 1,}&{{r_{\text{D}}} = \frac{r}{N};}
\end{array}$
|
(17)
|
外边界条件为
|
$\begin{array}{*{20}{c}}
{{{\left. {\frac{{\partial {p_{\text{D}}}}}{{\partial {x_{\text{D}}}}}} \right|}_{{x_{\text{D}}} = 0,{a_{\text{D}}}}} = 0,}&{{{\left. {\frac{{\partial {p_{\text{D}}}}}{{\partial {y_{\text{D}}}}}} \right|}_{{y_{\text{D}}} = 0,{b_{\text{D}}}}} = 0,}&{{{\left. {\frac{{\partial {p_{\text{D}}}}}{{\partial {z_{\text{D}}}}}} \right|}_{{z_{\text{D}}} = 0,{h_{\text{D}}}}} = 0}
\end{array}.$
|
(18)
|
2.3 方程求解
拉普拉斯变换能够把对时间的偏导数从不稳定渗流方程中消去,因而已经被广泛应用于求解不稳定渗流问题[22].对(13)式进行Laplace变换得
|
$\frac{{{\partial ^2}{{\tilde p}_{\text{D}}}}}{{\partial x_{\text{D}}^2}} + \frac{{{\partial ^2}{{\tilde p}_{\text{D}}}}}{{\partial y_{\text{D}}^2}} + \frac{{{\partial ^2}{{\tilde p}_{\text{D}}}}}{{\partial z_{\text{D}}^2}} + \frac{{4\pi }}{{s{N^2}}}f\left( {{x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}}} \right) = s{\tilde p_{\text{D}}}.$
|
(19)
|
对(19)式,分别对
xD,
yD,
zD进行Fourier余弦变换,并整理得
|
$\overline {\overline{\overline {{{\tilde p}_D}}} } = \frac{1}{{u_m^2 + v_n^2 + w_p^2 + s}}\frac{{4\pi }}{{s{N^2}}}f\left( {{u_m},{v_n},{w_p}} \right),$
|
(20)
|
式中,
um,vn,wp为以下方程组的解
|
$\left\{ \begin{gathered}
{u_m}\tan {u_m} - {a_{\text{D}}} = 0,\hfill \\
{v_n}\tan {v_n} - {b_{\text{D}}} = 0,\hfill \\
{w_p}\tan {w_p} - {h_{\text{D}}} = 0,\hfill \\
\end{gathered} \right.$
|
(21)
|
|
$f\left( {{u_m},{v_n},{w_p}} \right) = {F_1}{F_2}{F_3},$
|
(22)
|
|
${F_1} = \frac{{\left\{ {\sin \left[{{u_m}\left( {{x_{0{\text{D}}}} + {w_{x{\text{D}}}}} \right)} \right] - \sin \left[{{u_m}\left( {{x_{0{\text{D}}}} - {w_{x{\text{D}}}}} \right)} \right]} \right\}}}{{2{u_m}{w_{x{\text{D}}}}}},$
|
(23)
|
|
${F_2} = \frac{{\left\{ {\sin \left[{{v_n}\left( {{y_{0{\text{D}}}} + {w_{y{\text{D}}}}} \right)} \right] - \sin \left[{{v_n}\left( {{y_{0{\text{D}}}} - {w_{y{\text{D}}}}} \right)} \right]} \right\}}}{{2{v_n}{w_{y{\text{D}}}}}},$
|
(24)
|
|
${F_3} = \frac{{\left\{ {\sin \left[{{w_p}\left( {{z_{0{\text{D}}}} + {w_{z{\text{D}}}}} \right)} \right] - \sin \left[{{w_p}\left( {{z_{0{\text{D}}}} - {w_{z{\text{D}}}}} \right)} \right]} \right\}}}{{2{w_p}{w_{z{\text{D}}}}}}.$
|
(25)
|
通过Fourier余弦逆变换求得Laplace空间解
|
${P_{\text{D}}}\left( {{x_{\text{D}}}} \right) = \sum\limits_{m = 1} {\frac{{\cos \left( {{u_m}{x_{\text{D}}}} \right)}}{{{N_n}}}{{\bar P}_{\text{D}}}\left( {{u_m}} \right),} $
|
(26)
|
式中,
N(
n)为范数
|
$N\left( n \right) = \frac{1}{2}\left( {1 + \frac{{\sin {u_n}\cos {u_n}}}{{{u_n}}}} \right).$
|
(27)
|
(20)式先后对
zD,
yD,
xD进行Fourier余弦逆变换
|
$\begin{gathered}
s{{\tilde p}_{\text{D}}} = \frac{{4\pi }}{{{a_{\text{D}}}{b_{\text{D}}}{h_{\text{D}}}}}\left\{ {\frac{1}{s} + 2\sum\limits_{m = 1} {\cos \left( {{u_m}{x_{\text{D}}}} \right)\frac{{{F_1}}}{{\left( {s + u_m^2} \right)}} + 2\sum\limits_{n = 1} {\cos \left( {{v_n}{y_{\text{D}}}} \right)\frac{{{F_2}}}{{\left( {s + v_n^2} \right)}} + } } } \right. \\
4\sum\limits_{n = 1} {\sum\limits_{m = 1} {\cos \left( {{v_n}{y_{\text{D}}}} \right)\cos \left( {{u_m}{x_{\text{D}}}} \right)\frac{{{F_1}{F_2}}}{{\left( {s + u_m^2 + v_n^2} \right)}} + 2\sum\limits_{p = 1} {\cos \left( {{w_p}{z_{\text{D}}}} \right)\frac{{{F_3}}}{{\left( {s + w_p^2} \right)}} + } } } \\
4\sum\limits_{m = 1} {\sum\limits_{p = 1} {\cos \left( {{w_p}{z_{\text{D}}}} \right)\cos \left( {{u_m}{x_{\text{D}}}} \right)\frac{{{F_1}{F_3}}}{{\left( {s + u_m^2 + w_p^2} \right)}} + 4\sum\limits_{n = 1} {\sum\limits_{p = 1} {\cos \left( {{v_n}{y_{\text{D}}}} \right)\cos \left( {{w_p}{z_{\text{D}}}} \right)\frac{{{F_2}{F_3}}}{{\left( {s + v_n^2 + w_p^2} \right)}} + } } } } \\
\left. {8\sum\limits_{m = 1} {\sum\limits_{n = 1} {\sum\limits_{p = 1} {\cos \left( {{v_n}{y_{\text{D}}}} \right)\cos \left( {{w_p}{z_{\text{D}}}} \right)\cos \left( {{u_m}{x_{\text{D}}}} \right)\frac{{{F_1}{F_2}{F_3}}}{{\left( {s + u_m^2 + v_n^2 + w_p^2} \right)}}} } } } \right\}. \\
\end{gathered} $
|
(28)
|
由等式
|
$2\cos \left( {\alpha \beta } \right)\cos \left( {\alpha \gamma } \right) = \cos \left[{\alpha \left( {\beta + \gamma } \right)} \right] + \cos \left[{a\left( {\beta - \gamma } \right)} \right],$
|
(29)
|
|
$\sum\limits_{k = 1} {\frac{{\cos kx}}{{{k^2} + {\alpha ^2}}}} = \frac{\pi }{{2\alpha }}\frac{{\cosh \alpha \left( {\pi - x} \right)}}{{\sinh \left( {\alpha \pi } \right)}} - \frac{1}{{2{\alpha ^2}}},$
|
(30)
|
并利用式(29)~(30),式(28)可改写为
|
$\begin{gathered}
s{{\tilde p}_{\text{D}}} = \frac{{2\pi }}{{{a_{\text{D}}}{b_{\text{D}}}{h_{\text{D}}}}}\left\{ {\frac{{\left[{\cosh \sqrt s \left( {{b_{\text{D}}} - {y_{\text{D}}} + {y_{0{\text{D}}}}} \right) + \cosh \sqrt s \left( {{b_{\text{D}}} - {y_{\text{D}}} - {y_{0{\text{D}}}}} \right)} \right]}}{{\sqrt s \sinh \sqrt s {b_{\text{D}}}}}} \right. \\
2\sum\limits_{m = 1} {\cos \left( {{u_m}{x_{\text{D}}}} \right)\frac{{\cos \left( {{u_m}{x_{{\text{0D}}}}} \right)\sin \left( {{u_m}{w_{x{\text{D}}}}} \right)}}{{{u_m}{w_{x{\text{D}}}}}}} \frac{{\cosh {\tau _m}\left[{\left( {{b_{\text{D}}} - \left( {{y_{\text{D}}} - {y_{0{\text{D}}}}} \right)} \right.} \right] + \cosh {\tau _m}\left[{{b_{\text{D}}} - \left( {{y_{\text{D}}} + {y_{0{\text{D}}}}} \right)} \right]}}{{{\tau _m}\sinh {\tau _m}{b_{\text{D}}}}} \\
2\sum\limits_{p = 1} {\cos \left( {{w_p}{z_{\text{D}}}} \right)\frac{{\cos \left( {{w_p}{y_{0{\text{D}}}}} \right)\sin \left( {{w_p}{w_{z{\text{D}}}}} \right)}}{{{w_p}{w_{z{\text{D}}}}}}\frac{{\cosh {\tau _p}\left[{\left( {{b_{\text{D}}} - \left( {{y_{\text{D}}} - {y_{0{\text{D}}}}} \right)} \right.} \right] + \cosh {\tau _m}\left[{{b_{\text{D}}} - \left( {{y_{\text{D}}} + {y_{0{\text{D}}}}} \right)} \right]}}{{{\tau _p}\sinh {\tau _p}{b_{\text{D}}}}}} \\
4\sum\limits_{m = 1}^\infty {\sum\limits_{p = 1}^\infty {\cos \left( {{u_m}{x_{\text{D}}}} \right)\cos \left( {{w_p}{z_{\text{D}}}} \right)\frac{{\cos \left( {{u_m}{x_{0{\text{D}}}}} \right)\sin \left( {{u_m}{w_{x{\text{D}}}}} \right)}}{{{u_m}{w_{x{\text{D}}}}}}\frac{{\cos \left( {{w_p}{z_{0{\text{D}}}}} \right)\sin \left( {{w_p}{w_{z{\text{D}}}}} \right)}}{{{w_p}{w_{z{\text{D}}}}}}} } \\
\left. {\frac{{\cosh {\tau _{mp}}\left[{\left( {{b_{\text{D}}} - \left( {{y_{\text{D}}} - {y_{0{\text{D}}}}} \right.} \right)} \right] + \cosh {\tau _{mp}}\left[{{b_{\text{D}}} - \left( {{y_{\text{D}}} + {y_{0{\text{D}}}}} \right)} \right]}}{{{\tau _{mp}}\sinh {\tau _{mp}}{b_{\text{D}}}}}} \right\},\\
\end{gathered} $
|
(31)
|
式中,
|
$\begin{array}{*{20}{c}}
{{\tau _m} = \sqrt {s + u_m^2} ,}&{{\tau _p} = \sqrt {s + w_p^2} ,}&{{\tau _{mp}} = \sqrt {s + u_m^2 + w_p^2} .}
\end{array}$
|
(32)
|
式(32)即为具有不渗透区域、外边界封闭的各向异性均质矩形油藏部分射开压裂直井拉普拉斯空间下的解析解模型,通过Stehfest
[23]数值反演方法,可得到渗流压力的数值解.通过改变裂缝中心位置,即可得出不同位置处的裂缝的渗流压力.
3 流动期划分
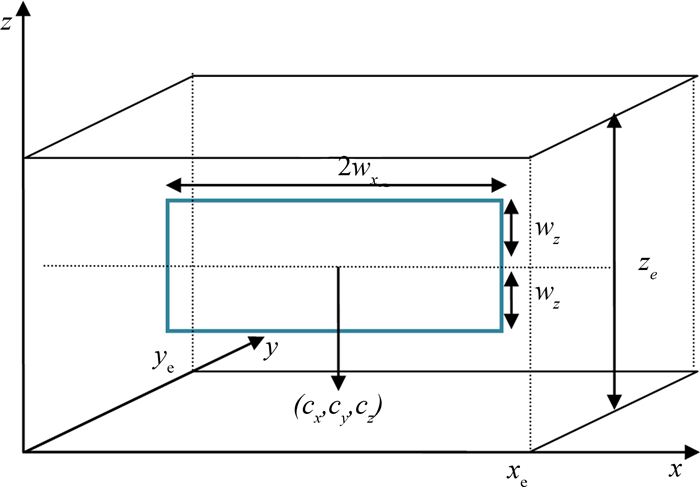
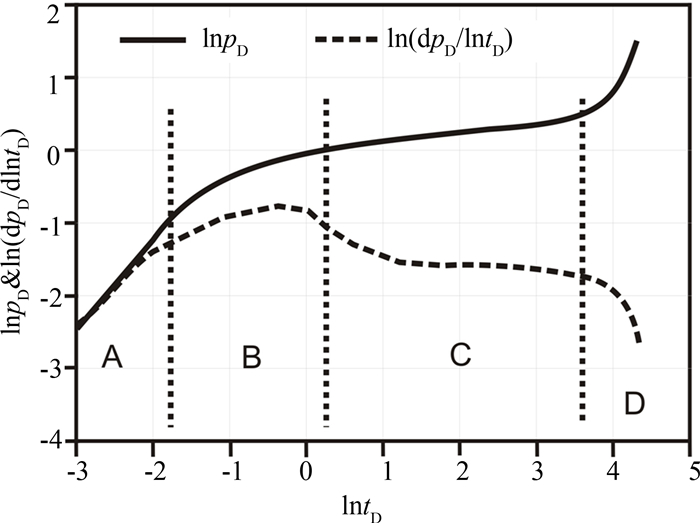
将裂缝中心坐标设在井轴中心线上,射开程度为50%,kx=ky,且kx/kz=100,压裂直井在储层中心压开一条裂缝,其它基本参数如表 1所示,研究井底渗流压力和压力导数变化趋势,如图 3所示.部分射开压裂直井渗流压力(压力导数)样板曲线可分为A(早期线性流)、B(中期径向流)、C(晚期球形流)、D(边界控制流)四个流动期.A阶段主要是表皮效应和井筒存储效应共同作用的结果,渐进分析表明,该阶段压力导数的曲线斜率约等于1,随着储层流体不断向井筒径向渗流,出现中期径向流,储层射开程度越高,则中期径向流作用的时间就越长.随着压力逐渐向外扩张,在压力未传播到边界之前,此时主要发生晚期球形流,压力导数变化逐渐变暖,直到趋于稳定.当压力传播到边界后,发生边界控制流,压力导数值变化加快,最终储层流体以拟稳态流的形式流向井筒.
表1(Table 1)
|
表1 计算所需参数表
Table 1 Basic parameters of the system
|
表1 计算所需参数表
Table 1 Basic parameters of the system
| 参数 | 值 | | 参数 | 值 |
| 原始饱和压力/MPa | 23 | 地层水密度/(g·cm-13) | 1 |
| 地层原油粘度/(mPa·s) | 0.56 | 地层原油体积系数 | 1.735 |
| 原始油藏压力/MPa | 23 | 原油密度/(g·cm-3) | 0.839 |
| 有效厚度/m | 20 | 油水界面深度/m | 3 000 |
| 地面原油粘度/(mPa·s) | 1.82 | 地层水体积系数 | 1.002 |
| 地层水粘度/(mPa·s) | 0.499 | 地层原油压缩系数/(10-4 MPa-1) | 33.98 |
| 岩石压缩系数/(10-4 MPa-1) | 4 | 地层水压缩系数/(10-4 MPa-1) | 4.5 |
|
 |
| 点击放大 |
4 模型论证
建立的数学模型可以求解多裂缝系统的压力,为简化论证,假设裂缝条数为10条.采用油藏数值模拟计算渗流场,然后输出不同时间、不同位置处的压力值(模拟解),并与文本的Stehfest[23]数值反演计算所得的渗流压力数值解(本文解)进行比较.
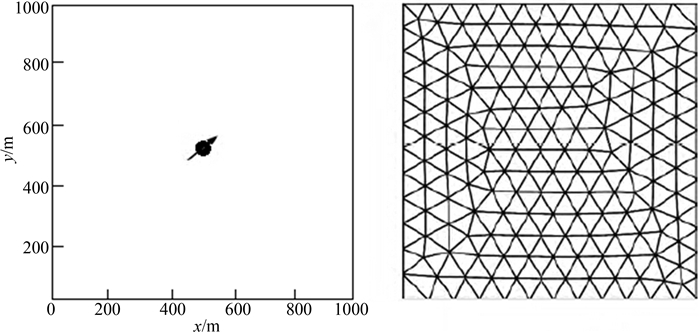
油藏数值模拟器Eclipse 2011中的E300模块,主要针对裂缝型非均质油藏而设立的,利用E300模拟一个矩形非均质油藏压裂直井周围的压力变化,油藏正中心有一口压裂直井生产,为满足式(1)假设条件,数值模拟采用五点井网,即油藏中心一口生产井,四个边界角点四口注入井,以保证生产井定流量生产,采用三角网格系统,保证每条裂缝长至少3个网格.因此,平面划分为20×20个网格,平均网格步长为50米,纵向根据裂缝条数划分为10个模拟层,模拟总网格数为20×20×10=4 000,如图 4所示.数值模拟和模型计算所需参数如表 1所示,两种方法计算结果如表 2所示.由表 2可知,相对误差基本控制在5%内,符合误差允许范围,说明本文所建模型是可靠的.
表2(Table 2)
|
表2 计算压力对比表
Table 2 Simulated and numerical pressures
|
表2 计算压力对比表
Table 2 Simulated and numerical pressures
| 时间/d | 模拟解/MPa | 本文解/MPa | 相对误差/% | | 时间/d | 模拟解/MPa | 本文解/MPa | 相对误差/% |
| 30 | 22.984 488 | 22.248 694 | 3.201 263 391 | | 210 | 21.278 916 | 20.557 576 | 3.389 928 322 |
| 60 | 22.603 428 | 21.870 262 | 3.243 605 352 | 240 | 21.087 072 | 20.365 732 | 3.420 768 896 |
| 90 | 22.273 614 | 21.539 134 | 3.297 534 024 | 270 | 20.909 682 | 20.196 226 | 3.412 084 411 |
| 120 | 21.981 906 | 21.251 368 | 3.323 360 586 | 300 | 20.722 656 | 19.911 828 | 3.912 760 992 |
| 150 | 21.723 048 | 20.992 512 | 3.362 962 693 | 330 | 20.538 039 | 19.731 153 | 3.928 739 253 |
| 180 | 21.490 471 | 20.766 502 | 3.368 786 257 | 360 | 20.353 422 | 19.450 478 | 4.436 325 253 |
|
 |
| 点击放大 |
5 敏感性分析
采用控制变量方法,利用表 1的参数,分别分析裂缝方位、裂缝规模、储层射开程度、渗透率各向异性、油藏边界条件、油藏规模等因素对井底压力和压力导数样板曲线(以下简称样板曲线)的影响.
5.1 裂缝方位的影响
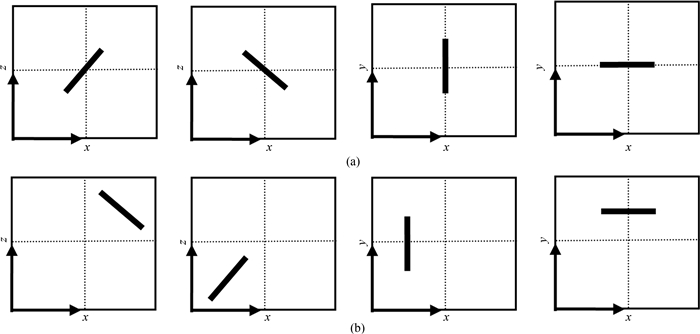
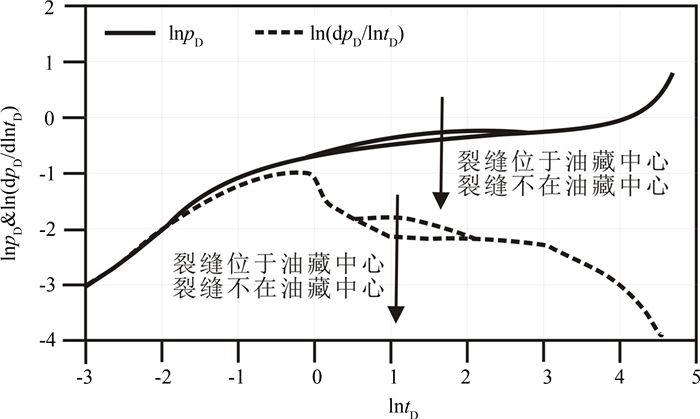
水力压裂压开的裂缝具有随机性,因而本文将裂缝的方位分为两个方面,即位于油藏中心(如图 5(a)所示)和不位于油藏中心(如图 5(b)所示),通过设置不同裂缝中心位置坐标来显示不同裂缝方位对样板曲线的影响,作出两种裂缝方位下无因次压力、压力倒数与无因次生产时间的双对数关系图版,如图 6所示.
图 6表明:裂缝方位主要影响样板曲线的晚期球形流阶段,当裂缝位于油藏中心时,压力更容易向外传播,主要是因为在晚期球形流阶段,储层流体以空间汇的形式从四周向生产井汇聚,水力压裂压开的裂缝是储层中建立的“流动网络”,联通储层更多的渗流通道,增大储层暴露的渗流面积,裂缝相对于中心越对称,则流体的流动通道就更简便,更易于流体渗流和压力的传播.
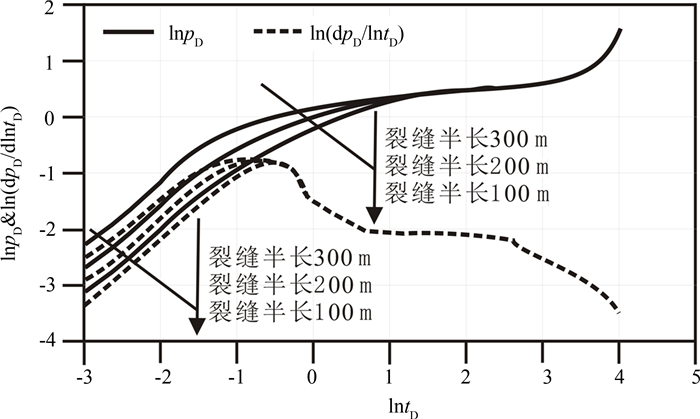
5.2 裂缝长度的影响
不同的压裂规模,形成裂缝的长度是不一样的.不同的裂缝长度,则储层暴露的渗流面积也不一样,因而压力传播趋势不同,如图 7所示.图 7表明:裂缝长度主要影响早期线性流和中期径向流,尤其是中期径向流.同一生产时间下,随着裂缝长度的增加,压力降落变缓,压力传播变快,压力增加显著.在早期线性流阶段,小的裂缝更容易产生大的压力降落,这是因为生产速率一定的情况下,裂缝规模越大,泄流面积就大,井筒的供液能力就强,在图形上就表现出早期线性流阶段的时间就越长.同一裂缝长度下,压力降落速度趋于一致,且裂缝长度只是影响早期线性流的时间,对于压力降落快慢,影响不明显.采用渐进分析,可知此阶段的直线段斜率为0.5.
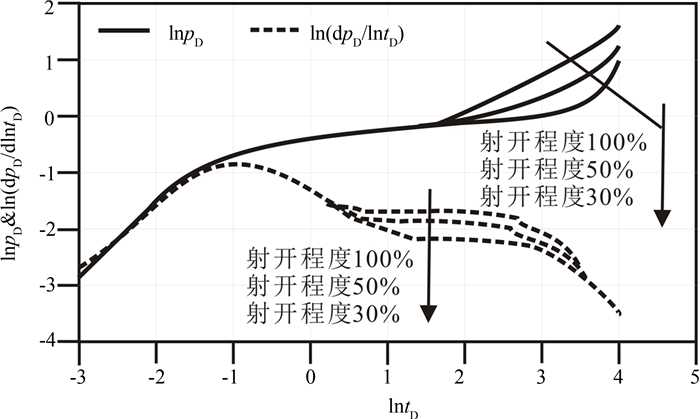
5.3 储层射开程度的影响
合理的储层射开程度,不仅可以节约射孔成本,而且还可以获得最大产量,射开程度对于储层流体压力影响较大,如图 8所示.图 8表明:射开程度主要影响样板曲线的晚期球形流末端和边界控制流的开始.当储层射开程度增大时,晚期球形流时间变短,流体渗流就更早进入边界控制流阶段.当储层完全射开时,流体几乎不经过球形流阶段,直接进入边界控制流阶段.
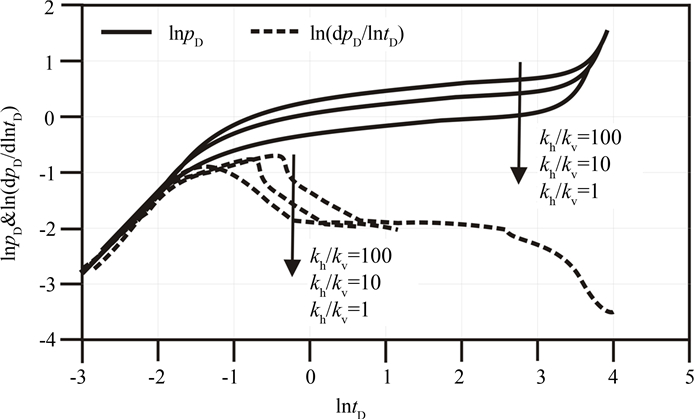
5.4 储层各向异性的影响
由于渗透率在水平方向上变化不大,因此将x、y方向上的渗透率视为一个值,研究垂向渗透率各向异性对样板曲线的影响,如图 9所示.图 9表明:渗透率垂向异性主要影响中期径向流阶段,这主要是因为在实际的地层中,垂向渗透率越大,则裂缝间发生流体渗流的概率就大,反之,则越小.因此当水平渗透率与垂向渗透率比值增大时,中期径向流的作用时间就越长,因为当水平渗透率起主导作用时,储层流体主要从水平方向渗流到井筒.
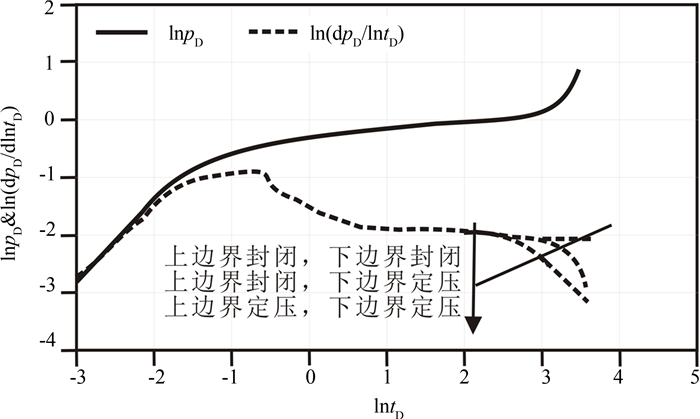
5.5 储层边界条件的影响
不同边界条件的组合,对于样板曲线的影响是不一样的,如图 10所示.图 10表明:边界条件主要影响边界控制流阶段.对于封闭边界,压力导数的值趋于稳定,渐进分析得出,此时压力导数约等于0.01;对于定压边界,由于近似有充足的外界能力供给,使得压力不断传播,压力导数逐渐降低,直到压力等于边界压力,渐进分析得出,此时压力导数斜率约为1,储层流体发生拟稳态渗流,对于上(下)边界封闭,下(上)边界定压,则处于以上两种情形之间,只是压力导数斜率不是一个常数.
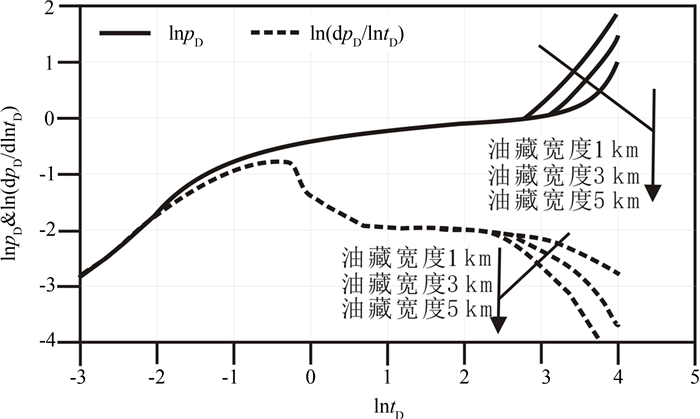
5.6 油藏宽度的影响
通过设置不同的油藏宽度,研究了油藏宽度对样板曲线的影响,如图 11所示.图 11表明:油藏宽度主要影响流体进入边界控制流阶段的时间和压力导数曲线在该阶段降低的快慢.随着油藏宽度的减小,渗流压力越早进入边界控制流阶段,而压力降落反而越小.主要是因为油藏宽度越小,则压力传播到边界所需的时间就小,在产量一定的情形下,渗流压力就必须更早进入边界控制流阶段,更早、更快的增加压力,提高生产压差,保持单位时间内流向井筒的流量一定.
6 结论
1) 通过建立符合非均质油藏部分射开地层实际的物理模型,推导了三维各向异性矩形油藏的不稳定渗流数学模型,该模型考虑了不渗透顶、底边界和定压顶、底边界等不同边界条件相互组合的情况.采用拉普拉斯变换、傅里叶余弦变换和斯蒂芬森数值反演方法等数学方法,得出模型实数域的压力数值解.计算结果与数值模拟基本吻合,证实了模型的正确性和求解方法的实用性.
2) 压力动态样板曲线可分为早期线性流、中期径向流、晚期球形流、边界控制流四个流动期.不同的油藏物性、不同的压裂施工规模均在不同程度上影响着渗流压力.其中裂缝长度主要影响早期线性流阶段,渗透率各向异性主要影响中期径向流阶段,储层射开程度和裂缝方位主要影响晚期球形流阶段,边界条件和油藏宽度主要影响边界控制流阶段.
3) 早期线性流阶段:压力和压力导数曲线为直线段,裂缝规模主要影响早期线性流,小的裂缝更易产生大的压力降落;中期期径向流阶段:压力和压力导数曲线表现为无线延伸系统有限井的径向流流动特征,压力导数近似平行于横坐标,为一常数;不渗透区域的大小和裂缝的方位决定了中期径向流出现和持续的时间;晚期球形流阶段:储层射开程度、裂缝方位决定了晚期球形流出现和持续的时间,储层流体向拟稳态渗流逼近,压力导数降落速率一定,约为0.5;边界控制流阶段:受边界条件类型和油藏边界的影响,反映压力波及范围.
4) 该方法可以确定最优射开程度、垂向渗透率等参数,为油藏工程分析和压裂工艺设计提供理论指导.



 2016, Vol. 33
2016, Vol. 33
