| 振动纤维捕集颗粒的格子Boltzmann模拟 |
近年来大气污染日益严重,尤其是悬浮颗粒物引起了国际社会的广泛关注.工程中常用的控制手段是加装布袋除尘器、振动纤维栅除尘器等设备,这类设备都是依靠纤维来捕集颗粒,纤维、流体与颗粒组成了一个复杂的流动系统.长久以来人们对这一问题进行了大量的理论、实验及数值研究.结果表明纤维对于颗粒的捕集机制主要分为拦截、惯性碰撞、布朗扩散、其它外力的作用[1, 2, 3].由于数值方法能够提供详细的流动信息及颗粒与流场之间相互作用细节,因而成为深入理解颗粒捕集机制的有效方法,并为改进这类设备提供理论指导,日益受到人们的关注.
在颗粒相比较稀疏的情况下,可以忽略颗粒对于流场的影响.通过流场模拟获得流场信息,将颗粒视为点源计算颗粒的受力与运动.本文流场模拟采用格子Boltzmann(LB)方法,该方法具有许多常规数值方法(如基于Navier-Stokes方程的模型)没有的优势,如边界容易处理,程序易于并行等优点,得到了广泛关注与使用[4, 5, 6, 7].国内外已经有许多基于LB方法的颗粒捕集的数值研究.Filippova等[8]首次应用LB方法和Lagrange跟踪方法模拟了颗粒在过滤器中的沉积过程,LB方法能够处理颗粒沉积在纤维表面形成的复杂表面,因而能够计算颗粒沉积导致系统压降的变化.Zarutskaya等[9]提出了新的颗粒运动模型来描述颗粒运动,该方程中颗粒的扩散不再通过布朗力来描述.在此基础之上,Lantermann等[10]进一步详细论述了范式力、静电力、布朗扩散对于颗粒捕集的影响.更加详细地分析了颗粒的运动与沉积过程.另一方面,Masselot等[11]提出了描述颗粒运动的格子气方法(LGA),该方法成功地应用于风对雪花沉积过程的影响、水底泥沙沉积形状等问题的研究.蔡新桃等[12]推广了LGA方法,使之能描述曳力,然后计算了方腔内颗粒的运动特性.王浩明等[13]进一步改进了LGA模型中的迁移概率的计算方法,然后对于不同Stokes数(St)、Peclet数(Pe)下颗粒的捕集效率与理论公式进行比较验证,系统研究了异形纤维的颗粒捕集等问题[14].但是上述研究局限于小雷诺数(Re).Yao等[15]和Brandon等[16]对于大雷诺数非定常流场中颗粒在尾涡中的弥散特性进行了研究,分析了St对颗粒弥散特性的影响.Haugen等[17]定量分析了不同St和Re时颗粒捕集效率的变化,着重分析了边界层厚度对于颗粒捕集角度与捕集效率的影响.提出了考虑边界层厚度的拟合公式.而Espinosa等[18]在研究纤维捕集颗粒时,发现被捕集颗粒的初始位置峰值并非出现在入口的中央位置,最终他们认为这是由上游流场的振荡引起的.
上述工作中均未考虑捕集体运动的影响.其实在颗粒捕集的实际的物理过程中,如布袋除尘器除尘、振动纤维栅除尘器除尘及风媒植物传粉工程中,捕集体会受到流体的作用产生运动,而捕集体的运动势必会影响颗粒运动.最近 Krick等[19]对植株捕集花粉的研究表明捕集体自身的运动对于颗粒的捕集效率有很重要的影响,并提出了一种新的“捕集体追赶机制”.但是该文研究的颗粒粒径在微米量级,且他们只关注捕集体横向运动对颗粒捕集效率的影响.在此基础上,本文采用格子Boltzmann方法模拟流向强迫振动的纤维捕集亚微米颗粒问题.另一方面,粒径在0.01 μm~3 μm之间的电厂粉尘最难捕集,结合Lantermann等[6]对0.001 μm~0.1 μm粒径颗粒的研究.因此本文重点研究了0.005 μm~0.5 μm的煤灰颗粒.参照文献[20],采用的Re为200,模拟了4组不同模态下的流向强迫振动纤维的颗粒捕集工况,对比分析不同工况时捕集效率、撞击角度分布、初始位置分布的变化.
1 数值方法本文中流场采用格子Boltzmann方法结合多块网格加细技术进行计算,颗粒运动采用Lagrange跟踪方法,并采用单项耦合描述流体-颗粒间的相互作用.
1.1 流场计算的格子Boltzmann(LB)方法LB方法将流体视为大量的微观粒子,这些粒子以特定规律在格点上碰撞迁移,最终通过统计可以得到流场的宏观物理量[21],对于本文的二维不可压流动问题,采用经典的D2Q9模型对流场进行模拟,其标准演化方程为
| ${f_i}\left( {x + {c_i}{\delta _t},t + {\delta _t}} \right) - {f_i}\left( {x,t} \right) = - \frac{1}{\tau }\left[{{f_i}\left( {x,t} \right) - f_i^{{\rm{eq}}}\left( {x,t} \right)} \right],$ | (1) |
其中fi(x,t)表示x位置处、t时刻、速度为ci的流体粒子的密度分布函数,τ为与流体粘度相关的无量纲松弛时间. fieq(x,t)为平衡态分布函数.为了抑制可压缩效应,本文采用的He-Luo不可压模型[22],平衡态分布函数为
| $f_i^{{\rm{eq}}}\left( {x,t} \right) = {\omega _i}\left[{{\rho _0} + \rho \left( {\frac{{{c_i} \cdot u}}{{c_{\rm{s}}^2}} + \frac{{\left( {{c_i} \cdot u} \right)}}{{2c_{\rm{s}}^4}} - \frac{{{u^2}}}{{2c_{\rm{s}}^2}}} \right)} \right].$ | (2) |
即υ=cs2(τ-0.5)δt,υ为流体的运动粘度,当地声速${c_{\rm{s}}} = c/\sqrt 3 $,ci为颗粒的迁移速度,c=δx/δt,δx和δt分别为空间、时间步长. ωi为权系数,D2Q9模型离散速度与权系数为
| ${c_i} = c\left[\begin{array}{l} 0\;\;1\;\;0\;\; - 1\;\;\;\;0\;\;1\;\; - 1\;\; - 1\;\;\;\;1\\ 0\;\;0\;\;1\;\;\;\;0\;\; - 1\;\;1\;\;\;\;\;1\;\; - 1\;\; - 1 \end{array} \right],$ | (3) |
| ${\omega _i} = \left[{\frac{4}{9}\;\;\frac{1}{9}\;\;\frac{1}{9}\;\;\frac{1}{9}\;\;\frac{1}{9}\;\;\frac{1}{{36}}\;\;\frac{1}{{36}}\;\;\frac{1}{{36}}\;\;\frac{1}{{36}}\;\;} \right].$ | (4) |
宏观密度与宏观速度的计算:
| $\begin{array}{*{20}{c}} {{p_i} = c_{\rm{s}}^2{f_i},}&{p = \sum\limits_i {{p_i},} }&{{p_0}u = } \end{array}\sum\limits_i {{p_i}{c_i}.} $ | (5) |
对于包含运动边界的问题,边界的运动会导致部分固体格点会成为流体格点,Ladd[23, 24]等假设颗粒内部也充满流体,计算过程中与外部流体遵循同样的演化方程.新出现的流体点就不需要赋值.Aidum等[25]提出一种去除内部流体的方法,该方法通过外推插值的方式获得新出现流体点的速度、密度及分布函数.本文采用后者.
为了准确模拟颗粒的运动,纤维附近流场计算需要较高的网格精度.同时为了兼顾计算量,本文的流体计算采用Yu等[26]提出的多块网格加细技术,粗细网格之间由重叠部分来实现信息的相互传递,为了保证粗细网格交界处的速度、密度、压力及其空间导数的连续性,对于粗细网格比为m的网格,粗细网格之间碰撞后的分布函数转换方程为
| $\tilde f_i^c = f_i^{{\rm{eq}},{\rm{f}}} + \frac{{m\left( {{\tau ^{\rm{c}}} - 1} \right)}}{{{\tau ^{\rm{f}}} - 1}}\left[{\tilde f_i^{\rm{f}} - f_i^{{\rm{eq}},{\rm{f}}}} \right],$ | (6) |
| $\tilde f_i^{\rm{f}} = f_i^{{\rm{eq}},{\rm{c}}} + \frac{{{\tau ^{\rm{f}}} - 1}}{{m\left( {{\tau ^{\rm{c}}} - 1} \right)}}\left[{\tilde f_i^{\rm{c}} - f_i^{{\rm{eq}},{\rm{c}}}} \right].$ | (7) |
其中上标f表示细网格上的值,c表示粗网格上的值.$\tilde f$表示碰撞后的分布函数值.
1.2 颗粒运动的Lagrange跟踪方法对于浓度较小的稀薄颗粒两相流,可以进行单项耦合计算,即忽略颗粒对于流体及颗粒之间的相互作用.Lagrange跟踪方法将颗粒视为点源[20],通过经验或者理论公式结合流场的计算数据,计算颗粒的受力,由运动方程积分得到颗粒的速度和位置.本文考虑的颗粒直径dp<1 μm,此时曳力与布朗力为主要作用力,同时忽略电磁力、重力、范式力、虚拟质量力及颗粒碰撞等的影响.颗粒的运动方程为
| ${m_{\rm{p}}}\frac{{{\rm{d}}{u_p}}}{{{\rm{d}}t}} = {F_{\rm{d}}}\left( {t,x\left( t \right)} \right) + {m_{\rm{p}}}A\left( t \right),$ | (8) |
| $\frac{{{\rm{d}}{x_{\rm{p}}}}}{{{\rm{d}}t}} = {u_{\rm{p}}}.$ | (9) |
其中mp、up、xp为颗粒的质量、速度与位置,Fd为流体的曳力,A为只与时间相关随机加速度项,用来表征颗粒的随机布朗运动.本文中的颗粒雷诺数比较小,曳力采用Stokes曳力公式计算,即Fd=mp/τp(uf-up),τp为颗粒松弛时间表征颗粒响应流场变化的快慢.当颗粒运动的时间步长${\delta _{{\rm{tp}}}} \ll {\tau _{\rm{p}}}$,认为在该时间内流场速度、外力项均为定值,进而可以对式(8)、(9)进行积分[9].
| ${\tau _{\rm{p}}} = \frac{{{\rho _{\rm{p}}}d_{\rm{p}}^2{C_{\rm{c}}}}}{{18\mu }},$ | (10) |
式中:μ为流体粘度,ρp、dp为颗粒的密度与直径.当dp与空气的平均自由程λ同量级甚至更小时,需要引入Stokes-Cunningham修正系数[10]
| ${C_{\rm{c}}} = 1 + \frac{{2\lambda }}{{{d_{\rm{p}}}}}\left( {1.257 + 0.4{{\rm{e}}^{ - 1.1{d_{\rm{p}}}/\left( {2\lambda } \right)}}} \right).$ | (11) |
其中,对颗粒的跟踪需要选取合适的δtp,应满足${\delta _{{\rm{tp}}}} \ll {\tau _{\rm{p}}}$,同时也要远大于周围流体分子与颗粒碰撞的时间尺度[26].颗粒中心与纤维表面距离小于等于颗粒半径时,颗粒被捕集.
2 数值模拟及结果分析 2.1 问题描述及参数选择考虑的问题如图 1所示,计算区域为60D×30D,D为纤维的直径,并设置20D×10D的局部加细网格计算区域,纤维的初始位置位于(12D,15D)处,沿来流(水平)方向做正弦振动,运动方程为xc=ADsin(2.0πfct),其中xc为纤维偏离初始位置的位移,频率fc=f0f,幅值AD,f0为静止纤维的涡脱落频率.粗网格步长δxc=1/20D,细网格的步长为粗网格的1/2.左边的为速度入口边界,右边边界速度梯度为零,上下边界为自由滑移边界,纤维表面为无滑移的壁面边界.外边界采用非平衡外推方法处理,纤维表面的边界采用Yu提出的曲面边界处理方法.颗粒的投放应该保证包含所有入口释放能被捕集的颗粒,因此入口处的阴影区域为颗粒的随机投放区域(本文的捕集效率可折算为常用的投放区域为纤维投影面积的效率),流场计算稳定之后,在trel=10Tc时间内(Tc为纤维强迫振动的周期),每一时间步都随机投放20个颗粒,当颗粒全部被捕集或运动出流场时,计算终止.
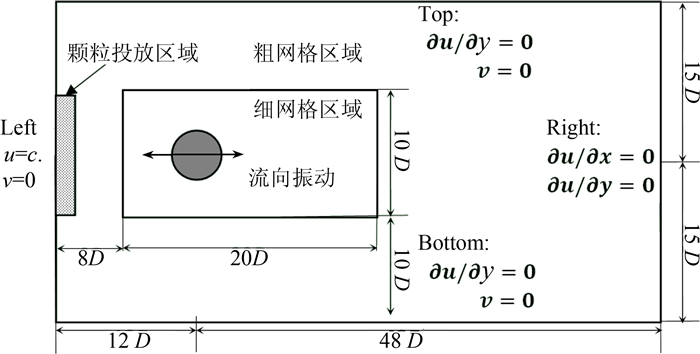 |
| 图1 模拟的计算区域图 Fig. 1 Definition of computational domain |
计算选用的流体为常温空气,颗粒为煤粉燃烧生成颗粒物,选用的实际物理参数如表 1所示,计算过程中需要将参数进行无量纲化[28],ρf为空气密度.
| 表1 模拟采用的气固两相流的物理参数 Table 1 Parameters settings of gas-solid flow simulation |
 |
| 点击放大 |
龚帅[20]等利用LB方法对Re=200的流向受迫振动问题进行了系统的研究,圆柱的运动方程xc=ADsin(2.0πfct).对于A=0.1D、A=0.3D时,不同振动频率的涡结构进行区分.根据上述研究结果,本文选取了4组具有代表性的f和A进行计算,随后的计算中将这四组频率与幅值作为本文的纤维振动参数.涡结构的模拟结果如表 2所示.
| 表2 计算中采用频率与振幅 Table 2 Frequency and amplitude |
 |
| 点击放大 |
为了保证计算模型的正确性,本文模拟了不同St数时的捕集效率与最大撞击角度.计算区域的设置与Haugen等[17]的一致,纤维位于12D×6D的计算区域的中心,上下边界为周期边界,固定密度比为1 000,此处St为Haugen等定义的,即St=ρpdp2CcU/9μD,其中U为入口处的流速,捕集效率η为捕集的颗粒数目ncap与投放颗粒总数ntot之比,撞击角度θ为撞击位置与圆心连线与来流反方向的夹角.验证的结果如图 2所示,可以看到本文的计算结果与文献结果十分吻合.
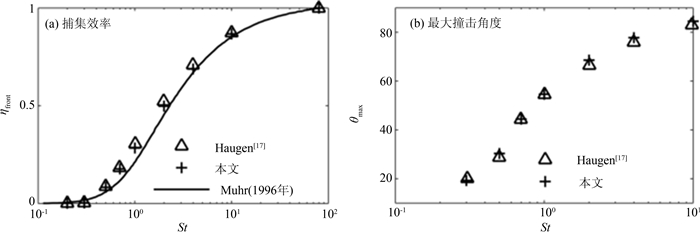 |
| 图2 不同St数时的捕集效率与最大撞击角度 Fig. 2 Capture efficiency and max hit angle at different St |
图 3为不同工况时,粒径分别为0.005、0.05和0.5微米的颗粒及涡量场的分布.dp=0.005 μm时,颗粒的松弛时间小表现出很好的跟随性,因而会被卷吸到尾涡中,此时布朗扩散的作用很强,会导致颗粒在尾涡中均匀分散.进而尾涡中的颗粒会被背风面捕集,并表现出很高的背风面捕集效率.dp=0.05 μm时,随着颗粒直径增大,颗粒的跟随性变差,虽然仍能进入尾涡,但是都分布在尾涡的边缘涡量较小的地方.当粒径达到0.5 μm时,尾涡中基本没有颗粒.背风面的捕集效率会降至最低.另外通过图 3各图的对比,不同的尾涡结构对于粒径为0.5 μm的颗粒影响最大.
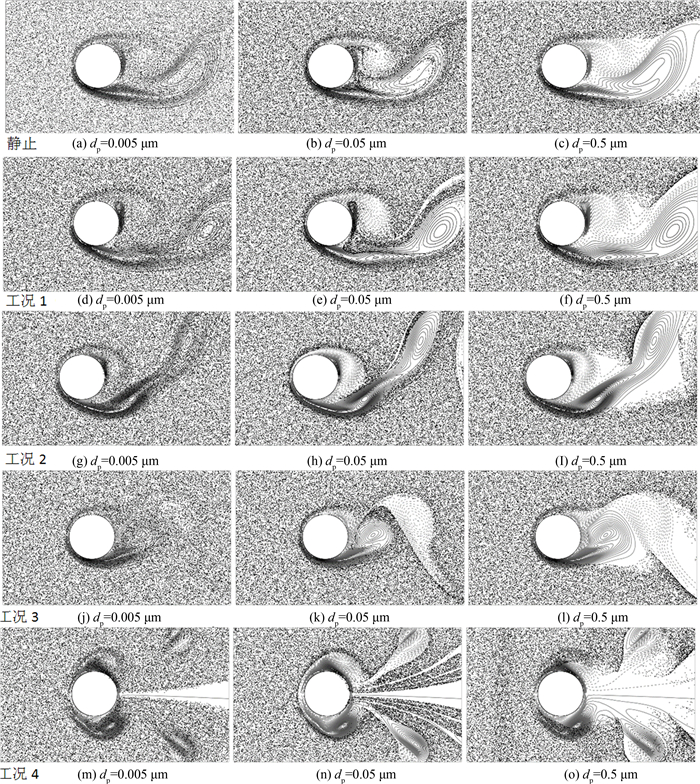 |
| 图3 不同工况时,流场的涡量场与颗粒分布,虚线为负涡,实线为正涡 Fig. 3 Contours of vorticity and distribution of particles in different cases |
图 4为不同工况时,颗粒的捕集效率随粒径的变化,纤维静止时随颗粒直径增加,捕集效率会先降低后增加,Lantermann等[10]对于Re较小的工况的研究发现了相似的趋势,在dp=0.5 μm附近颗粒的捕集效率会达到最小值.但是对于纤维振荡的工况,基本不会出现捕集效率下降段,且粒径的颗粒捕集效率会有6~39倍的提高,特别工况4时,颗粒的捕集效率要远优于其它工况.
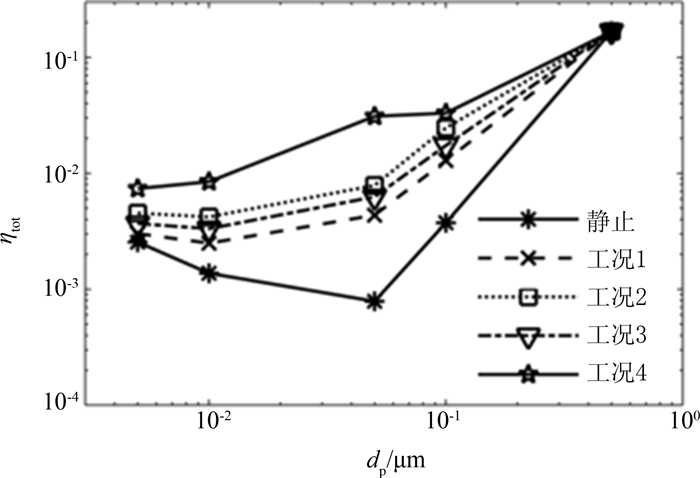 |
| 图4 不同工况下,不同粒径颗粒的捕集效率 Fig. 4 Capture efficiency with different diameters in different cases |
由于靠近纤维的颗粒必须穿越边界层才能接触到纤维表面,进而被捕集.小颗粒的松弛时间小,会沿流线绕过纤维.布朗力和惯性均能使颗粒偏离流线穿越边界层,这就是所谓的颗粒捕集的布朗机制与惯性机制.而拦截机制是指颗粒较大更容易接触纤维,在本文的研究中影响较小.所以纤维静止时,随着粒径的增大布朗作用减弱,dp<0.5 μm的颗粒的主要捕集机制—扩散机制会减弱,捕集效率会降低.dp>0.5 μm随着粒径的继续增加,颗粒惯性的增强和粒径的增加会使得拦截机制与惯性机制的效果增强,颗粒的捕集效率也会随之增加. Krick等[19]认为纤维自身的运动会改变颗粒相对纤维表面的速度,部分区域增大其它区域减弱,进而影响捕集效率,但是纤维的流向振动基本没有提升效果,而横向振动的提升效果比较显著.但是Krick等的分析中只考虑了相对运动速度的改变,没有考虑捕集体运动对于流动结构的影响.本文的模拟结果表明了流向振动也能够大幅度地提升颗粒的捕集效率.
为了更进一步分析捕集效率变化的原因,本文统计了纤维迎风面的捕集效率以及迎风面捕集的颗粒数目与捕集的总颗粒数目之比(Rfront).由图 5(a)可知,各工况迎风面的捕集效率差距不大.但是如图 5(b)所示,不同工况迎风面捕集的颗粒所占的份额的差距很大,其中在工况4时,迎风面捕集颗粒的份额远低于其它工况.
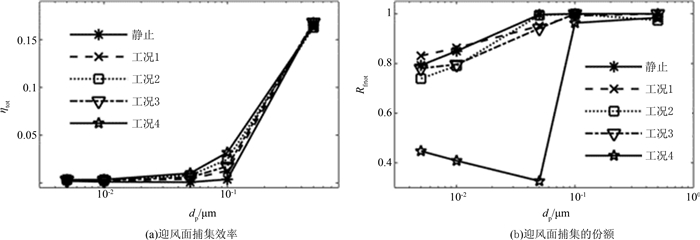 |
| 图5 不同工况下,不同粒径颗粒的迎风面捕集效率及其份额 Fig. 5 Front capture efficiency and share with different diameters in different cases |
我们统计了纤维背风面的捕集效率与背风面捕集颗粒所占的份额(Rfront),如图 6所示,工况4对于各个粒径的捕集效率均有很大的提升,但工况2只对于0.5 μm的颗粒才有明显的影响.其它工况捕集效率提升很少,工况1和3对于背部捕集效率的影响很小.
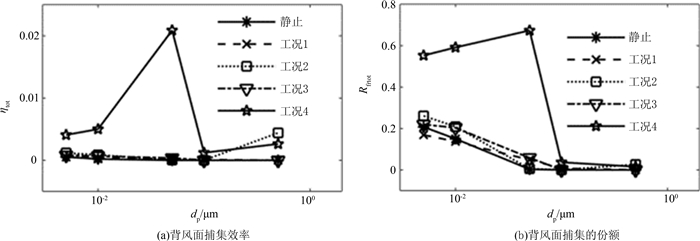 |
| 图6 不同工况下,不同粒径颗粒的背风面捕集效率及其份额 Fig. 6 Back capture efficiency and share with different diameters in different cases |
上述结果表明,不同工况对于迎风面与背风面的捕集效率影响不同,背风面捕集效率的差异更大.首先我们来考虑相对速度的影响,相对运动速度的大小与fcA成正比,虽然图 4总捕集效率的结果也表明,fcA越大,捕集效率越高.但是这不能表明相对运动速度改变起主导作用.一方面不同工况迎风面的捕集效率差距较小.由于上游的颗粒需要具有足够大的相对速度穿越迎风面的边界层而被捕集,即迎风面的捕集效率体现了相对运动速度对于捕集效率的影响相对较小;另一方面,不同工况的背部捕集效率相差较大,反映了流动结构改变对于颗粒运动的影响更大.这是因为在纤维下游,尾涡会卷吸颗粒回流,使得纤维的背风面能够捕集颗粒.而不同流动结构对于尾涡的影响更大.
2.3.3 颗粒的撞击角度分布图 7为被捕集颗粒的撞击角度的统计结果.颗粒的撞击角度为被捕集颗粒接触纤维的位置与圆心连线与入口流速方向的夹角,范围为-180°~180°;由于被捕集颗粒被投放位置的水平方向坐标对于捕集的影响可以忽略,此处只统计被捕集颗粒初始位置的竖直方向坐标的分布情况.
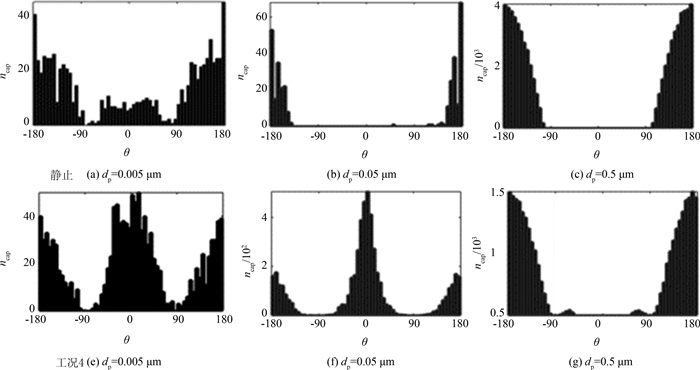 |
| 图7 不同工况下,不同粒径颗粒的撞击角度分布 Fig. 7 Distribution of hit-angle with different diameters in different cases |
纤维振动的撞击角度分布与静止工况有较大差异.以工况4为例,图 7所示颗粒撞击角度的分布与图 5、6中迎风面与背风面的效率统计是一致的.纤维静止时,大颗粒主要沉积在迎风面;随着颗粒变小,布朗运动增强,背风面开始出现颗粒的沉积.不同之处在于,静止工况时,dp=0.005 μm时才有颗粒沉积在纤维的背风面,但是工况4,dp=0.05 μm时就已经有颗粒沉积在背风面.
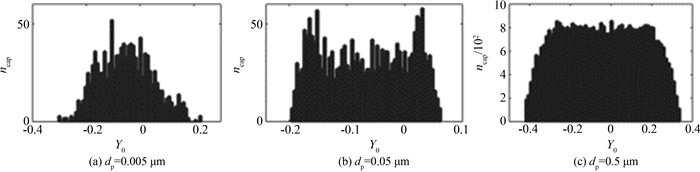
2.3.4 被捕集颗粒的初始位置的分布被捕集颗粒的初始位置的分布即“窗口”能够反映不同位置释放的颗粒捕集的难易程度,对于颗粒捕集过程具有指导意义.Esplnosa等[18]指出上游流场的振荡对于纤维附近颗粒的运动具有很重要的影响,会导致初始位置统计结果的峰值偏离入口中心位置,本文中同样发现该现象.
图 8所示的模拟过程中出现的3种具有代表性的分布形式,其中Y0=0代表入口的中心位置,图 8(a)、8(b)所示,初始位置都集中入口的中央,两端效率几乎没有.然而在图 8(c)统计结果的最高点基本关于中央对称,也就是说入口中央位置释放的颗粒并非是最容易捕集的.图 8(d)中,最高点仍在中央,但是在两端出现了对称的两个极值点.
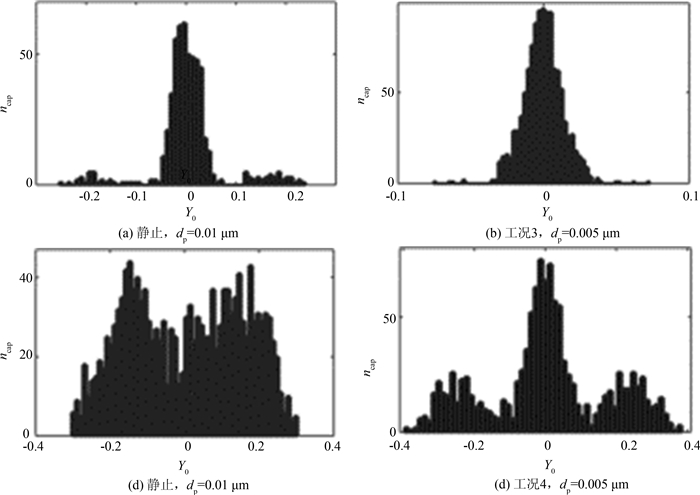 |
| 图8 不同工况下,被捕集颗粒的初始位置分布 Fig. 8 Distribution of initial position of captured particles |
图 9为工况2时被捕集颗粒的初始位置的统计结果.图 8中出现的统计结果都是关于Y0=0对称的形态,但是工况2即反对称AⅢ型涡结构时,被捕集颗粒的初始位置分布整体会偏离中心,由于其它的涡结构时,尽管瞬时的流场不对称,但是在一个周期的流动结构是对称变化的.而AⅢ形态的涡结构2Tc内脱落两个正涡和一个负涡,流场不是对称变化的,这种不对称效应的积累就会导致图 9中初始位置分布的不对称.
 |
| 图9 工况2,被捕集颗粒的初始位置分布 Fig. 9 Distribution of initial position of captured particles in Case 2 |
为了分析AⅢ形态时被捕集颗粒的初始位置分布偏离中心的原因,在入口的中心位置处0.04D宽度的区域投放颗粒,并记录某一时刻的颗粒分布以及涡量场信息.如图 10所示,其中左上角显示的是当前时刻的升阻力系数,在一个周期2Tc时刻内,只有在1/2Tc附近很短时间内颗粒才会经过纤维下方,其余时间颗粒都是经过纤维的上方.也就是说入口中央投放的颗粒大部分通过纤维的上方运动.这势必会导致入口上方区域投放的颗粒会在更上方运动,接触纤维的时间会更短.这就解释了被捕集颗粒的初始位置分布整体偏下的现象.
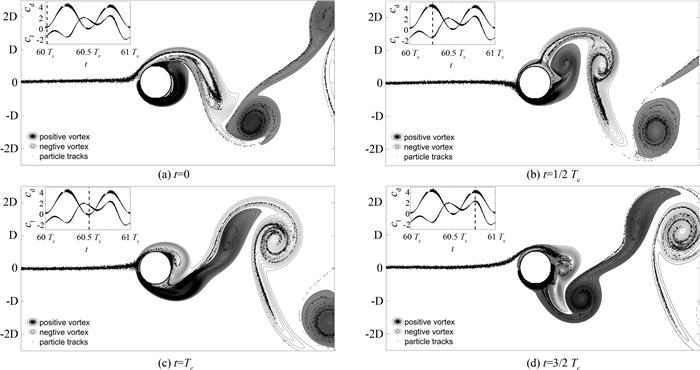 |
| 图10 工况2,dp=0.01 μm时,瞬时涡量场与颗粒分布 Fig. 10 Time snapshots in Case 2, dp=0.01 μm |
采用格子Boltzmann方法结合多块网格加细技术,对于Re=200的流向振动纤维捕集颗粒问题进行了模拟研究.验证了计算方法的精确度.计算了不同振动工况时不同粒径颗粒的捕集效率.发现纤维的流向振动能够显著提高亚微米颗粒的捕集效率.进而通过了颗粒撞击纤维的角度分布中发现,迎风面与背风面的颗粒的捕集效率明显不同.进一步对于被捕集颗粒的初始位置的统计过程中发现,在纤维静止、dp=0.1 μm等工况时,统计结果不是中央对称的单峰分布.特别是在AⅢ工况时,被捕集颗粒的初始位置的分布不再关于中心对称,而是整体会向下偏移.
| [1] | LEE K W, LIU B Y H. Experimental study of aerosol filtration by fibrous filters[J]. Aerosol Science and Technology, 1981, 1(1):35-46. |
| [2] | HADDADI H, SHOJAEI-ZADEH S, CONNINGTON K, et al. Suspension flow past a cylinder:particle interactions with recirculating wakes[J]. Journal of Fluid Mechanics, 2014, 760:R2. |
| [3] | 方鑫, 李珊红, 李彩亭,等. 布袋过滤除尘中气固两相流的格子Boltzmann模拟[J]. 环境工程学报, 2013,7(5):1883-1888. |
| [4] | MENG X, WANG L, GUO Z.Lattice Boltzmann simulation on carbonation of CaO with CO2[J].Chinese Journal of Computational Physics, 2014,31(2):173-184. |
| [5] | WANG H, ZHAO H, ZHENG C. Two-way coupling lattice Boltzmann model for gas-particle turbulent flows[J]. Chinese Journal of Computational Physics, 2013, 30(1):19-26. |
| [6] | HONG N, LI T, LI Q, SHI B. Lattice Boltzmann simulation of multiphase flows in a square cavity[J]. Chinese Journal of Computational Physics, 2013, 30(4):520-526. |
| [7] | NIE D, ZHENG M, ZHANG K. LB-DF/FD simulation of a drop-shaped particle in two dimensions settling in a vertical channel[J]. Chinese J Comput Phys, 2013,30(6):815-824. |
| [8] | FILIPPOVA O, HÄNEL D. Lattice-Boltzmann simulation of gas-particle flow in filters[J]. Computers & Fluids, 1997, 26(7):697-712. |
| [9] | ZARUTSKAYA T, SHAPIRO M. Capture of nanoparticles by magnetic filters[J]. Journal of Aerosol Science, 2000, 31(8):907-921. |
| [10] | LANTERMANN U, HÄNEL D. Particle Monte Carlo and lattice-Boltzmann methods for simulations of gas-particle flows[J]. Computers & Fluids, 2007, 36(2):407-422. |
| [11] | MASSELOT A, CHOPARD B. A lattice Boltzmann model for particle transport and deposition[J]. Europhys Lett, 1998, 42:259-264. |
| [12] | 蔡新桃, 郭照立, 郑林, 等. 方腔内微细颗粒物运动特性的格子Boltzmann方法模拟[J]. 计算物理, 2011, 28(3):355-360. |
| [13] | 王浩明, 赵海波, 郭照立, 等. 基于格子波尔兹曼气固两相流模型的清洁纤维捕集颗粒过程模拟[J]. 中国电机工程学报, 2012, 32(11):66-71. |
| [14] | 王浩明. 格子Boltzmann气固两相流模型及纤维捕集颗粒过程的数值模拟[D].武汉:华中科技大学,2013. |
| [15] | YAO J, ZHAO Y, HU G, et al. Numerical simulation of particle dispersion in the wake of a circular cylinder[J]. Aerosol Science and Technology, 2009, 43(2):174-187. |
| [16] | BRANDON D J, AGGARWAL S K. A numerical investigation of particle deposition on a square cylinder placed in a channel flow[J]. Aerosol Science & Technology, 2001, 34(4):340-352. |
| [17] | HAUGEN N E L, KRAGSET S. Particle impaction on a cylinder in a crossflow as function of Stokes and Reynolds numbers[J]. Journal of Fluid Mechanics, 2010, 661:239-261. |
| [18] | ESPINOSA A, GHISALBERTI M, ⅣEY G, et al. Numerical simulation of particle capture by circular cylinders[C]. 17th Australasian Fluid Mechanics Conference, 2010. |
| [19] | KRICK J, ACKERMAN J D. Adding ecology to particle capture models:Numerical simulations of capture on a moving cylinder in crossflow[J]. Journal of Theoretical Biology, 2015, 368:13-26. |
| [20] | 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京:科学出版社, 2009. |
| [21] | HE X, LUO L S. Lattice Boltzmann model for the incompressible Navier-Stokes equation[J]. Journal of Statistical Physics, 1997, 88(3-4):927-944. |
| [22] | LADD A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation[J]. Journal of Fluid Mechanics, 1994, 271:285-309. |
| [23] | LADD A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results[J]. Journal of Fluid Mechanics, 1994, 271:311-339. |
| [24] | 龚帅, 郭照立. 流向振荡纤维绕流的格子Boltzmann方法模拟[J]. 力学学报, 2011, 43(1):11-17. |
| [25] | AIDUN C K, LU Y. Lattice Boltzmann simulation of solid particles suspended in fluid[J]. Journal of Statistical Physics, 1995, 81(1-2):49-61. |
| [26] | YU D, MEI R, SHYY W. A multi-block lattice Boltzmann method for viscous fluid flows[J]. International Journal for Numerical Methods in Fluids, 2002, 39(2):99-120. |
| [27] | CHEN S, CHEUNG C S, CHAN C K, et al. Numerical simulation of aerosol collection in filters with staggered parallel rectangular fibres[J]. Computational Mechanics, 2002, 28(2):152-161. |
| [28] | 何雅玲,王勇,李庆. 格子Boltzmann方法的理论及应用[M]. 北京:科学出版社, 2009. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33

