2. Insititute of Energy Science and Engineering, Hangzhou Dianzi University, Hangzhou 310018, China
雷诺方程在连续相湍流的数值模拟中被广泛应用,湍流数值模拟的零方程模型、单方程模型、双方程模型、雷诺应力模型、代数应力模型等层出不穷,这些模型都是以平均Navier-Stokes方程为基础,而平均Navier-Stokes方程本身是不封闭的,需要附加各种近似假设和经验公式加以封闭,由于其本身具有无法克服的缺陷,他们的使用范围具有很大的局限性,比较具有代表性的标准 k-ε 模型[1]是以Boussinesq假设为基础,它只对高雷诺数的湍流有效,而且对模拟旋流和绕流也有缺陷.
与连续相雷诺方程类似,离散相雷诺方程也在数值模拟中被广泛采用,其核心思想是在Euler体系中构造方程使统计矩方程封闭,Reeks基于概率密度函数(PDF)框架得到双流体模型方程[2],利用Chapman-Enskog近似法得到三阶矩方程使模型封闭.Simonin[3]也采用概率密度函数方法推导颗粒的统计矩方程, Minier 和Perano[4]以及Minier和Pozorski[5]由PDF输运方程推导出类似雷诺展开得到的双流体模型,包括两相雷诺应力和湍流动能输运方程,用代数方程对不封闭的方程组加以封闭.van Slooten,Jayesh[6]仿照Rodi方程对雷诺应力方程进行处理,得到了颗粒应力代数方程,与颗粒相的连续方程、动量方程组成封闭的方程组.国内的周力行等人先后提出的 k-ε-kp 模型[7]、统一二阶矩模型[8]、代数应力模型[9],都采用经验公式或者近似假设,与连续相雷诺方程一样,其适用范围自然受到种种限制。
两相湍流流动的另外一种处理思路是离散相在Lagrange体系下采用颗粒的轨道方法,连续相依然采用雷诺方程数值模拟,这是一种非常重要并被广泛采用的计算方法,Xu和Pope[10],Li和Modest[11]以及柳朝晖[12]等人都曾采用常规的或者改造的Monte Carlo方法模拟两相湍流流动,Monte Carlo方法已经广泛用于颗粒随机轨道模型中.另外,徐江荣等先后建立了颗粒正应力轨道模型[13]和颗粒两阶矩轨道模型[14].Lagrange方法是求解PDF方程比较精确的方法,而且其封闭相对简单,但是要获得光滑连续的曲线往往需要计算大量颗粒的轨道,其光滑性也不如Euler方法。
两相湍流流动的Euler-Euler方法和Euler-Lagrange方法有各自的优点和局限性,本文试图有效地结合这两种方法,利用Lagrange方法易于封闭的优点,以Lagrange模型为基础推导模型的封闭形式,这与以往的仅在Euler体系中构造模型的思路不同,与以往的统计矩模型相比,新模型具有更为广泛的使用范围和更大的发展潜力,而且本文的研究可以为封闭模型提供一种新思路。
1 两相湍流颗粒二阶矩模型采用PDF方法给出两相湍流颗粒统计矩方程,典型的颗粒PDF输运方程为
| $\frac{{\partial {{\rm{P}}^r}}}{{\partial t}} + \frac{{\partial {U_{pi}}{P^r}}}{{\partial {x_i}}} - \frac{\partial }{{\partial {U_{pi}}}}\left[ {\left( {\frac{{{U_{pi}} - \left\langle {{U_{si}}} \right\rangle }}{{{\tau _p}}}} \right){P^r}} \right] + \frac{{\partial {g_i}{P^r}}}{{\partial {U_{pi}}}} = \frac{\partial }{{\partial {U_{pi}}}}\left[ {{\lambda _{ij}}\frac{{\partial {P^r}}}{{\partial {x_j}}} + {\mu _{ij}}\frac{{\partial {P^r}}}{{\partial {U_{pj}}}}} \right],$ | (1) |
定义颗粒数密度 np=∫P(x,Up,t)dUp, 对PDF输运方程(1)积分可以得到任意阶宏观矩方程,给出连续方程和动量方程
| $\left\{ \begin{array}{l} \frac{{\partial {n_p}}}{{\partial t}} + \frac{{\partial {n_p}\left\langle {{U_{pi}}} \right\rangle }}{{\partial {x_i}}} = 0,\\ \frac{{\partial \left\langle {{U_{pi}}} \right\rangle }}{{\partial t}} + \left\langle {{U_{pj}}} \right\rangle \frac{{\partial \left\langle {{U_{pi}}} \right\rangle }}{{\partial {x_j}}} = - \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial {x_j}}} + \frac{{\left\langle {{U_{si}}} \right\rangle - \left\langle {{U_{pi}}} \right\rangle + {\tau _p}{g_i}}}{{{\tau _p}}} - \left( {\left\langle {{u_{pi}}{u_{pj}}} \right\rangle + {\lambda _{ij}}} \right)\frac{1}{{{n_p}}}\frac{{\partial {n_p}}}{{\partial {x_j}}}. \end{array} \right.$ | (2) |
方程组(2)是基于方程式(1)的两阶矩Euler模型,(2)式中第一式是颗粒浓度方程,第二式是颗粒相平均速度方程,它含有不封闭项 〈upiupj〉, 若再由PDF输运方得到二阶矩方程,又将引入新的不封闭项,以往的做法是采用近似假设构造新方程使(2)式封闭,近似假设和经验公式只适用于特定的条件和流场,使模型不具有通用性,它的使用范围和发展空间都受到经验和假设的制约.
2 颗粒二阶矩模型的封闭颗粒运动Langevin方程[16]是PDF输运方程和统计矩模型的共同基础,对Langevin方程组系综平均可以得到平均Langevin方程[17]
| $\left\{ \begin{array}{l} \frac{{d\left\langle {{x_{pi}}} \right\rangle }}{{dt}} = \left\langle {{U_{pi}}} \right\rangle ,\\ \frac{{d\left\langle {{U_{pi}}} \right\rangle }}{{dt}} = \frac{1}{{{\tau _p}}}\left( {\left\langle {{U_{si}}} \right\rangle - \left\langle {{U_{pi}}} \right\rangle } \right) + {g_i},\\ \frac{{d\left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{dt}} = \frac{2}{{{\tau _p}}}\left( {\frac{{{\mu _{ij}} + {\mu _{ji}}}}{2} - \left\langle {{u_{pi}}{u_{pj}}} \right\rangle } \right). \end{array} \right.$ | (4) |
文[17]还从另外一种思路得到与之完全相同的结果,并利用方程组(4)对气固两相流场进行数值模拟,取得了理想的结果,方程组(4)在理论上和实践中都被证明是可靠的.对方程组(4)继续变形得到
| $\frac{{d\left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{dt}} = \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial t}} + \left\langle {{U_{pk}}} \right\rangle \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial {x_k}}} = \frac{2}{{{\tau _p}}}\left( {\frac{{{\mu _{ij}} + {\mu _{ji}}}}{2} - \left\langle {{u_{pi}}{u_{pj}}} \right\rangle } \right).$ | (5) |
方程式(5)只含有颗粒平均速度和二阶矩,没有其它不封闭量出现, 结合方程组(2)得到封闭的二阶矩模型
| $\left\{ \begin{array}{l} \frac{{\partial {n_p}}}{{\partial t}} + \frac{{\partial {n_p}\left\langle {{U_{pi}}} \right\rangle }}{{\partial {x_i}}} = 0,\\ \frac{{\partial \left\langle {{U_{pi}}} \right\rangle }}{{\partial {\rm{t}}}} + \left\langle {{U_{pj}}} \right\rangle \frac{{\partial \left\langle {{U_{pi}}} \right\rangle }}{{\partial {x_j}}} = - \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial {x_j}}} + \frac{{\left\langle {{U_{si}}} \right\rangle - \left\langle {{U_{pi}}} \right\rangle + {\tau _p}{g_i}}}{{{\tau _p}}} - \left( {\left\langle {{u_{pi}}{u_{pj}}} \right\rangle + {\lambda _{ij}}} \right)\frac{1}{{{n_p}}}\frac{{\partial {n_p}}}{{\partial {x_j}}},\\ \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial t}} + \left\langle {{U_{pk}}} \right\rangle \frac{{\partial \left\langle {{u_{pi}}{u_{pj}}} \right\rangle }}{{\partial {x_k}}} = \frac{2}{{{\tau _p}}}\left( {\frac{{{\mu _{ij}} + {\mu _{ji}}}}{2} - \left\langle {{u_{pi}}{u_{pj}}} \right\rangle } \right). \end{array} \right.$ | (6) |
以(5)式对不封闭的统计矩方程(2)加以封闭,推导过程是严格的,没有采用经验或半经验公式.方程的推导基于Lagrange模型,这一点与以往的在Euler体系中寻求封闭模型的思路不同.
3 两相壁面射流流场[8]的数值模拟两相壁面射流是一个典型的两相湍流流动[18],其流场特征参数见表1,计算区域见图1.本文采用混合二阶矩模型(Hybrid Second-order Moment Model,HSM)和有限分析/颗粒方法(Finite Analytic/Monte Carlo,FA/MC)[11]计算,连续相的计算采用标准 k-ε 模型,求解方法采用SIMPLE算法,计算网格数为175×100。
| 表1 流场特征参数 Table 1 Character of the cas |
 |
| 点击放大 |
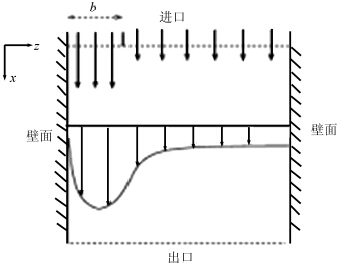 |
| 图1 壁面射流几何尺寸 Fig. 1 Geometry of wall jet test case |
图2为颗粒平均速度的计算结果与实验值的比较.计算结果十分理想,由图可知,HSM模型的计算结果与实验值更加符合,并且比FA/MC方法的计算结果更为光滑,HSM模型优于FA/MC方法。
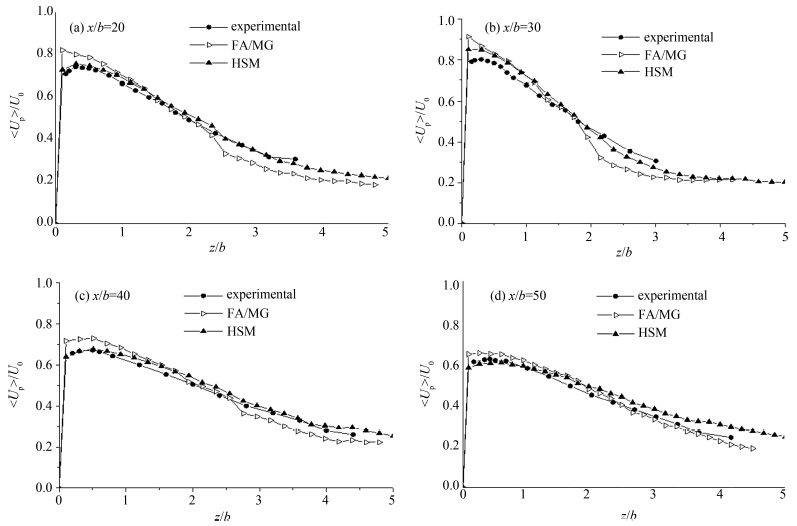 |
| 图2 颗粒平均速度的计算值与实验值 Fig. 2 Profiles of particle mean vertical velocities |
图3是颗粒脉动速度的对比分析,两种方法的颗粒脉动速度与实验值基本符合,HSM模型的计算结果更接近实验值,而且HSM模型依然可以获得更为光滑的计算结果。
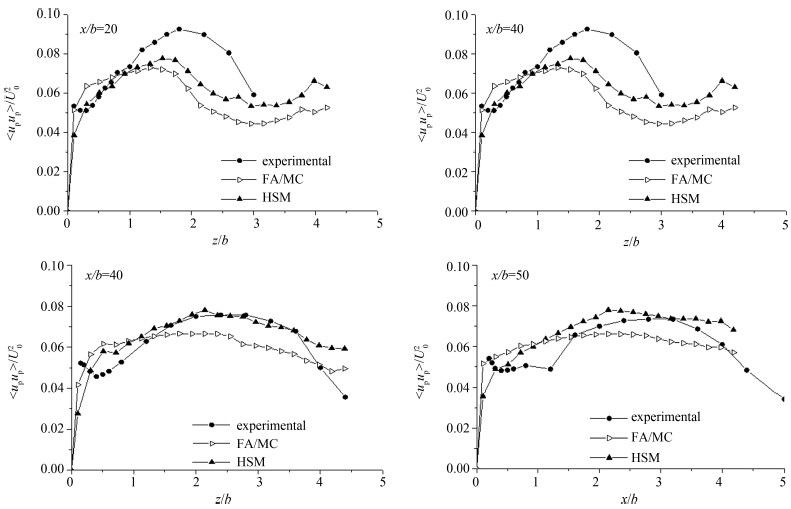 |
| 图3 颗粒脉动速度计算值与实验值 Fig. 3 Profiles of particle fluctuating vertical velocities |
图4给出了颗粒浓度的计算结果,与FA/MC方法相比,HSM模型的计算结果有所改善,新模型更加光滑的特点进一步得到体现,但在计算精度上仍然有一定的提升空间.
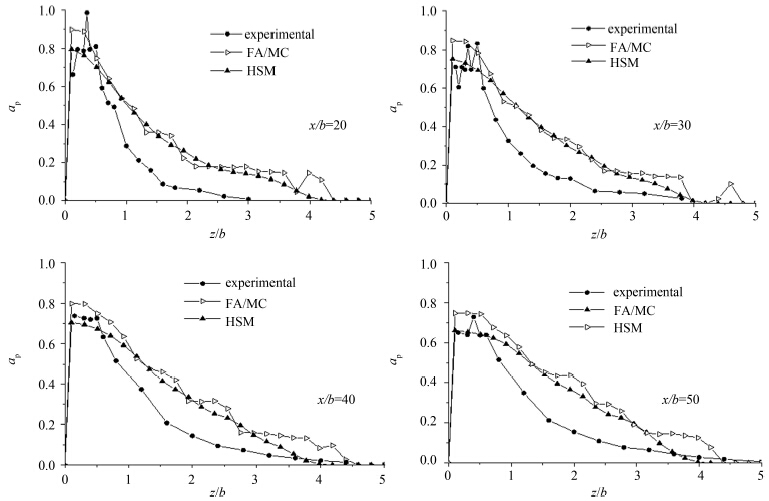 |
| 图4 颗粒浓度的计算值与实验值 Fig. 4 Profiles of particle volumetric fraction |
用Lagrange方法封闭的统计矩模型给出的混合二阶矩模型,不需附加其它近似假设,该方法具有更为广泛的使用潜力,可以为模型的不封闭问题提供新思路.根据对两相壁面射流流场的计算可知,新模型的计算结果整体优于有限分析/颗粒方法,计算结果更加准确合理,而且曲线更为光滑。
| [1] | ZHANG Z S, CUI G X, XU C X. Theory and modeling of turbulence [M]. Beijing: Tsinghua University Press, 2005:209-216. |
| [2] | REEKS M W. On the continuum equations for dispersed particles in non-uniform flows [J]. Phys Fluids A, 1992, 4(6): 1290-1302. |
| [3] | SIMONIN O, DEUTSCH E, MINIER J P. Eulerian prediction of the fluid-particle correlated motion in turbulent two-phase flows [J]. Flow, Turbulence and Combustion, 1993, 51(1-2): 275-283. |
| [4] | MINIER J P, PEIRANO E. The PDF approach to turbulent poly-dispersed two-phase flows [J]. Physics Reports, 2001, 352(1): 1-214. |
| [5] | POZORSKI J, MINTER J P. On the Lagrangian turbulent dispersion models based on the Langevin equation[J]. International Journal of Multiphase Flow, 1998, 24(6): 913-945. |
| [6] | van SLOOTEN P R, JAYESH Pope S B. Advances in PDF modeling for inhomogeneous turbulent flows [J]. Physics of Fluids, 1998, 10(1): 246-265. |
| [7] | ZHOU L X, LIN W Y, SUN K M. Simulation of swirling gas-particle flows using USM and k-ε-kp two-phase turbulence models [J]. Journal of Engineering Thermophysics, 1995, 4: 481-485. |
| [8] | ZHOU L X, CHEN T. Simulation of swirling gas-particle flows using the unified second-order moment model [J]. Acta Mechanica Sinica, 1998, 30(4): 385-390. |
| [9] | ZHOU L X. A unified correlation moment closure model of turbulent gas-particle flows and combustion [J]. Journal of Engineering Thermophysics, 1991, 12(2): 203-209. |
| [10] | XU J, POPE S B. Assessment of numerical. accuracy of PDF/Monte carlo methods for turbulent reacting flows [J]. Journal of Computational Physics, 1998, 152:192-230. |
| [11] | LI G, MODEST M F. An Effective particle tracing scheme on structured/unstructured grid in hybrid finite volume/PDF monte carlo methods[J]. Journal of Computational Physics, 2001, 173:187-207. |
| [12] | LIU Z H, ZHENG C G, ZHOU L X. A DSM-LPDF two-phase turbulence model and Monte-Carlo simulation of swirling two-phase flow [J]. Journal of engineering thermophysics, 2001, 22(5):641-644. |
| [13] | XU J R, ZHOU Z J, et al. Particles Reynolds stresses trajectory model and numerical simulation for a backward-facing step two-phase flow [J]. Chinese Journal of Computational Physics, 2004, 21(6): 538-542. |
| [14] | XU J R, WANG L. Two-order moment trajectory model of two-phase turbulence flow based on particle PDF transport equation[J]. Applied Mechanics and Materials, 2014, 668-669: 318-321. |
| [15] | MINIER J P, PEIRANO E. The PDF approach to turbulent poly-dispersed two-phase flows[J]. Physics Reports, 2001, 352(1): 1-214. |
| [16] | RISKEN H. The fokker-planck equation: Methods of solution and applications [M]. New York: Springer,1989. |
| [17] | WANG L. A two-order moment Lagrange model based on PDF two-phase theory and its simulation [D]. Hangzhou: Hangzhou Dianzi University,2013. |
| [18] | SATO Y, HISHIDA K, MAEDA M. Effect of dispersed phase on modification of turbulent flow in a wall jet [J]. Journal of Fluids Engineering, 1996, 118: 307-315. |
 2016, Vol. 33
2016, Vol. 33


