| 火星进入器小攻角飞行的静不稳定性 |
美国火星科学实验室(Mars Science Laboratory,MSL)成功在火星登陆后,印度也成功向火星发射了环绕探测器,针对火星的深空探测活动又开始在世界范围内活跃起来.未来大量的火星进入及登陆任务,以及火星采样返回、载人登陆和火星基地建设等计划,都要求对火星大气环境下探测器进入的气动特性做出准确预测[1, 2, 3, 4].陌生的大气环境、技术手段的局限和基础数据的缺乏都对气动特性预测带来了极大的挑战.
以美国为例,对火星进入气动特性的预测经历了以试验为主到以计算为主,计算方面也经历了由简单模型至复杂模型的变化过程.NASA首次成功登陆火星的进入器是海盗号(Viking)1号和2号,它们均以约10°配平攻角进入火星大气[5].当时受限于计算流体力学(Computational Fluid Dynamics,CFD)的发展水平,海盗号的飞行前气动特性评估主要采用地面试验数据,附加CO2大气环境修正.随后的火星探路者号(Mars Pathfinder,MPF)和火星探索漫游者号(Mars Exploration Rovers,MER)等都采用0°攻角进入方式,此时的气动特性评估则几乎全部基于CFD预测结果[6, 7, 8],没有开展关于气动特性的地面实验研究.及至最近成功的火星科学实验室,由于质量显著增加又重新采用了升力式进入方案,其飞行前气动评估与飞行后数据重建依旧以CFD计算为主.可见计算流体力学在火星进入气动力特性预测中扮演了极其重要的作用.
火星大气气动预测对CFD带来的极大挑战来源于和地球完全迥异的大气环境.火星大气主要由95.7%的CO2、2.7%的N2和1.6%的Ar组成,密度只有地球大气的十分之一至百分之一,温度也较地球大气更低,因此飞行器进入火星大气和再入地球大气完全不同.针对火星大气的CFD模拟需要重新建立适应的物理、化学模型,针对地球大气建立的数值模型和方法也需要考察其用于火星大气环境模拟的适用性.和NASA数十年的理论、数值和实验相结合的研究相比,国内对火星大气进入的研究刚刚起步[9].虽然已有的CFD技术经过了地球再入等问题的考验[10],但火星进入相关的物理化学模型目前只能由文献得到,需要深入分析来完成验证和掌握,解决火星进入中面临的问题,更重要的是发现并解决新的问题.
通过Viking飞行数据验证高温气体模型与数值计算方法,针对MPF探测器沿飞行轨道开展三维数值研究,通过比较分析小攻角飞行时进入器的气动系数及其变化规律,掌握CFD模型对气动力特性预测的实用性,着重探讨2°攻角飞行时进入器沿轨道出现的静不稳定现象及和机理,对于火星探测具有支撑作用.
1 模型和方法 1.1 几何模型选用火星探路者号为研究对象,由于后体对火星探测器气动特性的影响非常小,因此只考虑进入器前体,如图 1所示,具体尺寸参考文献[11].特征长度取前体直径2.65 m,参考面积为前体面积,质心位置为xcg=0.662 m.图 1右是采用的表面网格.
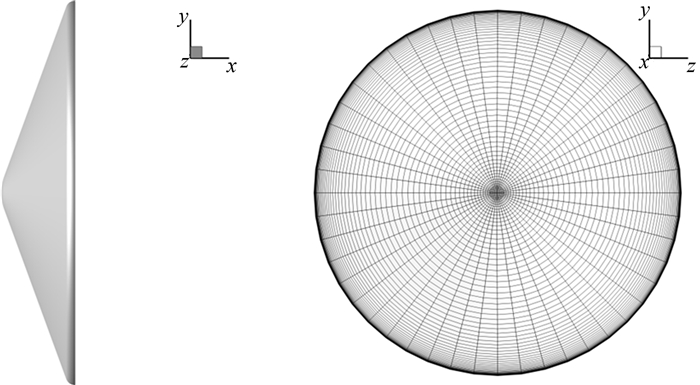 |
| 图1 MPF前体模型与表面网格 Fig. 1 Geometry mode and surface mesh of MPF forebody |
流动考虑层流状态,直角坐标系下的三维可压缩层流Navier-Stokes方程可以写为
| $ \begin{array}{l} \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} + \frac{{\partial H}}{{\partial z}} = \frac{{\partial {F_V}}}{{\partial x}} + \frac{{\partial {G_V}}}{{\partial y}} + \frac{{\partial {H_V}}}{{\partial z}} + S,\\ U = \left\{ \begin{array}{l} {\rho _i}\\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{array} \right\},F = \left\{ \begin{array}{l} {\rho _i}u\\ \rho {u^2} + p\\ \rho uv\\ \rho uw\\ u\left( {\rho E + p} \right) \end{array} \right\},C = \left\{ {\begin{array}{*{20}{c}} {{\rho _i}u}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {\rho vw}\\ {v\left( {\rho E + p} \right)} \end{array}} \right\},H = \left\{ {\begin{array}{*{20}{c}} {{\rho _i}w}\\ {\rho uw}\\ {\rho vw}\\ {\rho {w^2} + p}\\ {w\left( {\rho E + p} \right)} \end{array}} \right\},\\ {F_v} = \left\{ {\begin{array}{*{20}{c}} {{D_i}\frac{{\partial {\rho _i}}}{{\partial x}}}\\ {{\tau _{xx}}}\\ {{\tau _{xy}}}\\ {{\tau _{xz}}}\\ {{\tau _{xx}}u + {\tau _{xy}}v + {\tau _{xz}}w - {q_x}} \end{array}} \right\},{G_v} = \left\{ {\begin{array}{*{20}{c}} {{D_i}\frac{{\partial {\rho _i}}}{{\partial y}}}\\ {{\tau _{yx}}}\\ {{\tau _{yy}}}\\ {{\tau _{yz}}}\\ {{\tau _{yx}}u + {\tau _{yy}}v + {\tau _{yz}}w - {q_y}} \end{array}} \right\},\\ {H_v} = \left\{ {\begin{array}{*{20}{c}} {{D_i}\frac{{\partial {\rho _i}}}{{\partial z}}}\\ {{\tau _{zx}}}\\ {{\tau _{zy}}}\\ {{\tau _{zz}}}\\ {{\tau _{zx}}u + {\tau _{zy}}v + {\tau _{zz}}w - {q_z}} \end{array}} \right\},S = \left\{ {\begin{array}{*{20}{c}} {{{\dot \omega }_i}}\\ 0\\ 0\\ 0\\ 0 \end{array}} \right\} \end{array} $ |
数值算法方面,对流项采用AUSM+-up格式[12],其中界面值通过使用minmo d限制器的MUSCL方法得到;粘性项采用二阶中心格式;时间推进采用LU-SGS方法.
1.3 热化学模型完全气体模型参数由CO2气体给定,比热比取等效比热比.
真实气体模型的热力学参量,如比热cP、焓H等,输运系数,如粘性系数μ、热传导系数k、扩散系数Di等,均通过温度拟合多项式得到.混合气体的对应参数由Wilke公式计算.化学反应源项通过有限速率化学反应模型得到,若将化学反应写作
| $ \sum\limits_{i=1}^{ns}{V_{ij}^{f}{{R}_{i}}}\rightleftharpoons \sum\limits_{i=1}^{ns}{V_{ij}^{b}{{R}_{i}}},\ \ \ \ j=1,\cdots ,nr, $ |
| $ {{\dot \omega }_i} = {M_i}\sum\limits_{j = 1}^{nr} {\left( {V_{ij}^b - V_{ij}^f} \right)} \left\{ {\sum\limits_{n = 1}^{ns} {{\lambda _{jn}}} \left[ {{X_n}} \right]} \right\}\left( {k_j^f\prod\limits_{n = 1}^{ns} {{{\left[ {{X_n}} \right]}^{V_{nj}^f}}} - k_j^b\prod\limits_{n = 1}^{ns} {{{\left[ {{X_n}} \right]}^{V_{nj}^b}}} } \right), $ |
考虑到火星大气中CO2和N2占绝对多数,且CO2和CO的热非平衡松弛过程非常迅速,因此在忽略热非平衡效应的假设下,将Park反应模型简化为8组分(CO2,CO,O2,O,C,N2,N,NO)、 9反应的化学反应动力学模型.具体反应如表 1所示,反应常数参见文献[13].
| 表1 化学反应 Table 1 Chemical reactions |
 |
| 点击放大 |
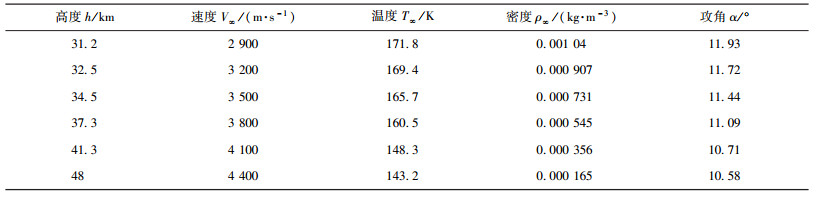
选择海盗号飞行试验数据和NASA通用代码LAURA的计算结果验证方法与模型.表 2所列为计算中选用的海盗号飞行轨道中的典型状态点.
| 表2 验证算例计算状态 Table 2 Computational conditions in validation |
 |
| 点击放大 |
图 2展示了海盗号外形,以及h=41.3 km状态所得Ma数等值面和飞行器周围气流轨迹.空间流线显示气体穿过飞行器前部弓形激波后受到强烈压缩,绕过肩部后在飞行器底部和尾迹流动中呈现出涡运动等复杂流动特征.
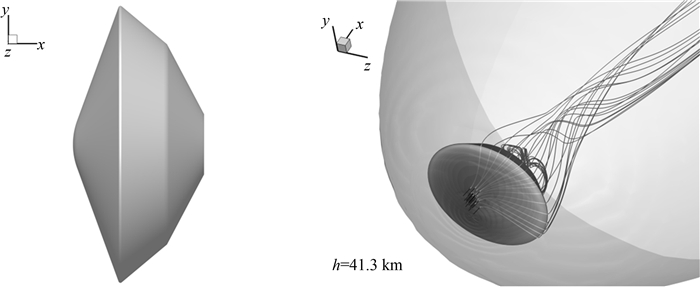 |
| 图2 海盗号外形及空间流线和Ma等值面 Fig. 2 Configuration of Viking: Space streamlines and Ma iso-surfaces |
图 3是海盗号升力和阻力系数的飞行数据、LAURA结果和本文计算结果的比较,可见现有结果和飞行数据符合很好,升力系数预测值和LAURA一致,在低Ma数范围较飞行数据稍低.阻力系数和LAURA结果变化规律一致,偏差保持稳定,约1.2%,但比LAURA结果更接近飞行数据,最大偏差约为3%.验证了所用的物理化学模型、数值方法和程序代码.
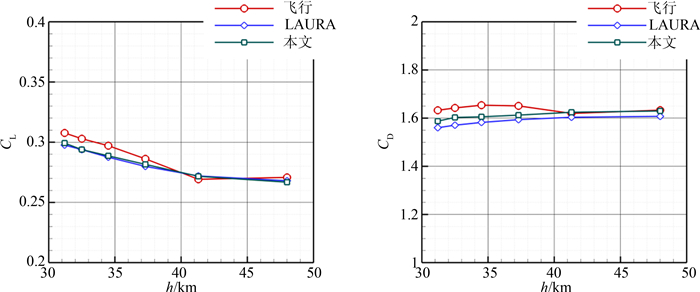 |
| 图3 海盗号升力和阻力系数验证 Fig. 3 Validation of lift and drag coefficients of Viking |
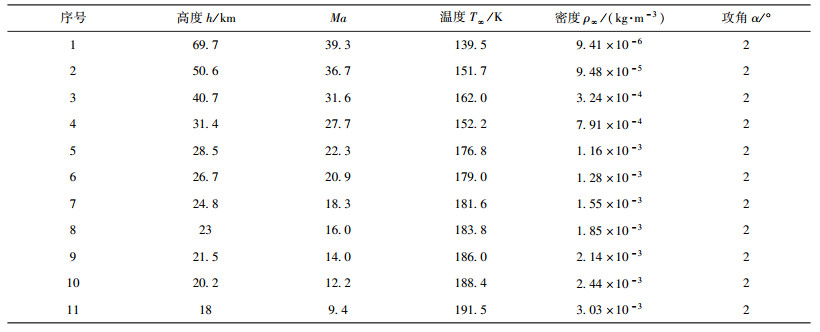
MPF计算状态为其飞行轨道,具体参见表 3.壁面取无滑移等温条件,TW=700 K.
| 表3 MPF计算状态 Table 3 Computational conditions for MPF |
 |
| 点击放大 |
图 4是MPF的升力和阻力系数沿轨道的变化.结果显示真实气体模型预测结果和LAURA的计算结果非常接近,与Viking验证算例一致,升力系数二者完全相符,阻力系数偏差不超过1.2%,证实了模型和方法的适用性.完全气体模型的升力系数和复杂模型的结果非常接近,而阻力系数较为平坦,偏差稍大.在飞行过程中,随高度下降飞行器周围的气体经历平衡-非平衡-冻结的变化过程,其比热比会呈现先减小后增大的变化,即激波后流动压缩性先加强后减弱,表现为阻力系数先上升后下降,真实气体模型预测结果准确反映了这一规律.
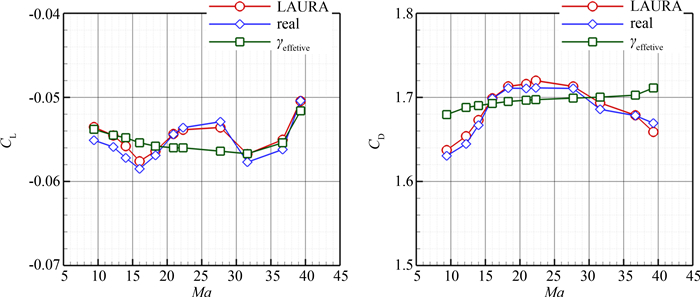 |
| 图4 MPF升力系数和阻力系数沿轨道变化 Fig. 4 Lift and drag coefficients of MPF along trajectory |
图 5是MPF俯仰力矩系数沿轨道的变化.由于俯仰力矩系数本身数值非常小,对计算模型的要求也就更高.同样的,复杂模型结果非常接近,显示出飞行器在沿轨道下降过程中出现两处静不稳定区域,而完全气体模型的预测值均约等于0,接近配平状态.
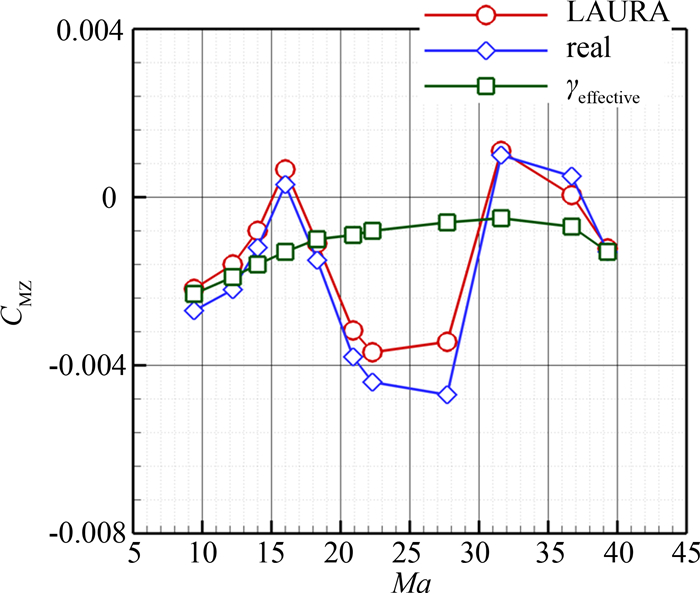 |
| 图5 MPF俯仰力矩系数沿轨道变化 Fig. 5 Pitching moment coefficient of MPF along trajectory |
图 6是沿轨道6个不同状态下真实气体模型和完全气体模型得到的对称面亚声速区分布情况.可见,真实气体模型得到的流场内,亚声速区随着轨道下降呈现周期变化规律,而完全气体模型的结果显示各状态的亚声速区域基本没有变化.由真实气体模型得到的亚声速区分布情况来看,首先是大面积亚声速区完全包裹背风区和迎风区,和边界层完全融合.随后,背风区亚声速区变化为一个区域泡,和边界层割离,而迎风面声速线向鼻部方向略有移动.Ma数继续降低后,背风区边界层外已完全是超声速流动,迎风面亚声速区域也受到压缩,声速线位置相比较稍微更加远离肩部.随着Ma数进一步下降,背风区从无亚声速区到出现亚声速区域泡、再到完全的大面积亚声速区.迎风区声速线位置则反向运动,变为逐渐更加靠近肩部.考虑到肩部膨胀区后压力下降非常剧烈,若存在较大的亚声速区覆盖肩部附近区域,将导致压力变化向上游传导,改变表面压力分布,进而造成配平特性和静稳定特性的变化.
 |
| 图6 不同Ma数MPF对称面亚声速区分布 Fig. 6 Subsonic area on symmetric plane with different Mach number |
图 7和图 8是3个典型状态的亚声速线分布和表面压力系数在对称面的变化曲线.迎风面肩部附近由于声速线位置差异,导致低Ma数状态压力系数存在较长的平台,随着Ma数的增大,压力系数平台区域减小,靠近肩部压力明显下降的范围扩大.对于背风区,Ma数越高锥面压力系数越大,由于Ma=27.7状态无亚声速区,压力系数在肩部以前均保持大致不变; Ma=36.7状态存在较大亚声速区域,因此从靠近肩部位置压力系数即出现明显下降; Ma=31.6状态出现亚声速区泡,肩部膨胀区对上游影响有限,故肩部压力系数反而高于Ma=36.7状态,在锥面近似分布平稳,这一差别正是造成俯仰力矩变为抬头力矩的原因.因此,飞行器俯仰力矩系数先增大后减小,即高温气体效应导致的声速线位置移动和亚声速区分布变化是造成飞行器出现静不稳定的主要原因.
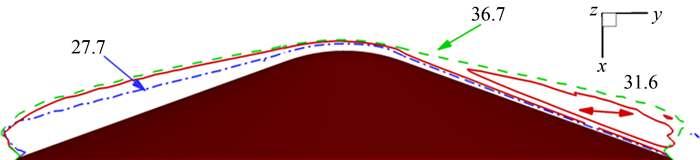 |
| 图7 对称面声速线 Fig. 7 Subsonic line on symmetric plane |
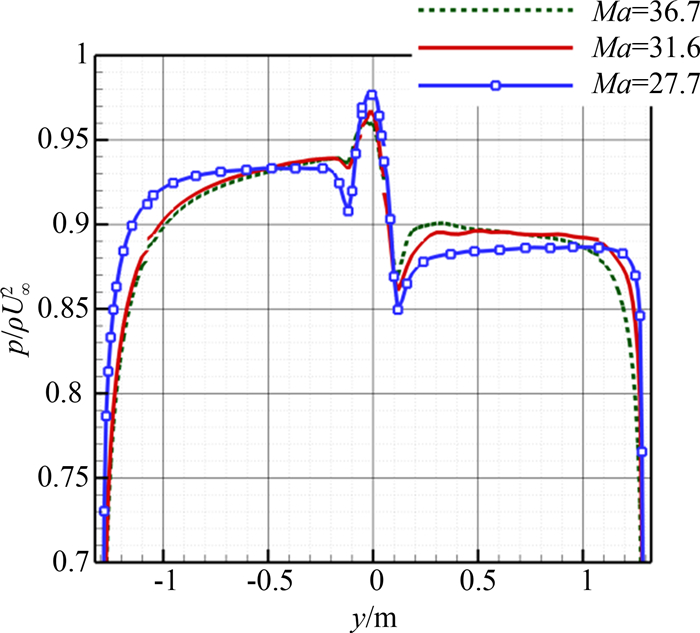 |
| 图8 对称面飞行器表面压力系数 Fig. 8 Surface pressure coefficient on symmetric plane |
通过三维数值模拟,分别采用真实气体模型和完全气体模型对探测器进入火星大气进行了流场解算和气动预测,与飞行数据和文献结果进行了对比,并分析了飞行器升阻特性和配平特性的变化规律,得到以下结论:
1) Viking预测升阻特性同飞行数据最大偏差不超过3%,和LAURA结果偏差1.2%,验证了物理化学模型和数值计算方法;
2) MPF小攻角飞行时,真实气体模型预测气动特性和LAURA结果符合很好,偏差1.2%,保持稳定,证明了模型和方法对不同探测器和飞行轨道的适用性.采用等效比热比的完全气体模型所得结果与复杂模型较为接近,但对细节变化的模拟明显不足,无法反映真实流动中的物理化学过程;
3) 进入器在小攻角飞行时,沿轨道存在静不稳定现象,完全气体模型无法模拟;通过机理分析发现,激波层内高温气体效应导致的声速线位置移动和亚声速区分布变化,以及这种变化沿轨道所表现的周期性,是造成静不稳定的主要原因.
| [1] | BRAUN R D, MANNING R M. Mars exploration entry, descent and landing challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2):310-323. |
| [2] | WRIGHT M J, TANG C Y, EDQUISK K T, et al. A review of aerothermal modeling for mars entry missions[R]. AIAA paper 2010-443, 2010. |
| [3] | DRUGUET M C. Prediction of the flow field over an orbiter entering the Mars atmosphere[J]. Shock Waves, 2010, 20(3):251-261. |
| [4] | VIVIANI A, PEZZELLA G. Aerodynamic analysis of a capsule vehicle for a manned exploration mission to Mars[R]. AIAA paper 2009-7386, 2009. |
| [5] | INGOLDBY R N, MICHEL F C, FLAHERTY T M, et al. Entry data analysis for Viking Landers 1 and 2 final report[R]. NASA CR-159388, 1976. |
| [6] | GNOFFO P A, BRAUN R D, WEILMUENSTER K J, et al. Prediction and validation of Mars Pathfinder hypersonic aerodynamic database[J]. Journal of Spacecraft and Rockets, 1999, 36(3):367-373. |
| [7] | GNOFFO P A, WEILMUENSTER K J, BRAUN R D, et al. Influence of sonic-line location on Mars Pathfinder Probe aerothermodynamics[J]. Journal of Spacecraft and Rockets, 1996, 33(2):169-177. |
| [8] | SCHOENENBERGER M, CHEATWOOD F M, DESAI P N. Static aerodynamics of the Mars Exploration Rover entry capsule[R]. AIAA Paper 2005-0056, 2005. |
| [9] | LV J, MIAO W, CHENG X, et al. Impact of trajectory deviations on aerodynamic characteristics of Mars Science Laboratroy[J]. Chinese J Comput Phys, 2014,31(6):668-674. |
| [10] | MIAO W, HUANG F, CHENG X, et al. Plasma prediction of reentry vehicle and gas components[J]. Chinese J Comput Phys, 2015,32(1):27-32. |
| [11] | GUPTA R N, LEE K P, SCOTT C D. Aerothermal study of Mars Pathfinder aeroshell[J]. Journal of Spacecraft and Rockets, 1996, 33(1):61-69. |
| [12] | LIOU M S. A sequel to ASUM, Part Ⅱ:AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 214(1):137-170. |
| [13] | PARK C, HOWE J, JAFFE R, et al. Review of chemical-kinetic problems of future NASA missions, Ⅱ:Mars entries[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1):9-23. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
