| 跨音速自然层流翼型多目标优化设计 |
现代中远途民用客机和高空高速长航时无人机巡航状态的阻力主要由摩擦阻力和升致阻力构成,分别占总阻力的55%和35%左右[1].飞机的总阻力每减小1%,直接使用成本可以降低0.2%或者增加1.6吨的有效载荷[2].目前,在跨音速状态下,层流化是能够大幅度减小摩擦阻力的有效方法.研究表明:飞机机翼表面层流区域从10%扩到90%弦长时,航程可以增加近50%;或者说减少一半以上的起飞重量[3].
超临界翼型的发展,使得飞机在跨音速状态下能够实现较高的升阻比,所以跨音速大展弦比飞机都采用中等后掠角的超临界机翼.然而在飞行雷诺数约107条件下,后掠翼极易诱发前缘附着线转捩及边界层展向流的不稳定,从而使机翼过早地发生转捩进入到湍流状态,大大增大了飞机的摩擦阻力[4].但是大展弦比超临界机翼的设计是高空高速长航时无人机的需要,拥有成熟的跨音速自然层流翼型/机翼设计技术,会极大地延长高空长航时无人机的留空时间,使其具备持久的情报收集和战场监视能力;另外对于民航客机而言,层流化技术不仅可以减小CO2的排放量,亦可提高运营效率[5].
自从第一架飞机问世以来,到目前为止还没有一架层流飞机被投入航线服务于人类,由此可见层流飞机设计的复杂性[4].层流翼型设计的难点之一就是流动转捩位置的准确预测.经过科研工作者几十年的努力,人们从实验、理论以及数值计算上对流动的转捩机理以及预测方法进行了较为详细的研究,取得了丰硕的成果.
自然层流翼型设计的关键就是使翼型表面保持大范围的顺压梯度,然而在跨音速状态下,层流翼型表面流向大范围顺压梯度的存在,使得翼型后缘因压力恢复产生较强的激波,在减小摩擦阻力的同时又增加了激波阻力,反而消弱了层流化的效果,因此应用多目标优化方法解决层流翼型设计过程中遇到的转捩位置和激波强度相互矛盾的问题.使用基于线性稳定性理论的eN方法作为转捩判断的工具,鼓包控制激波技术弱化翼型后缘的激波强度,进而基于多目标优化方法在推迟翼型表面转捩位置降低摩擦阻力的同时优化鼓包外形(高度、位置和长度)来控制后缘激波,得到带激波控制的自然层流翼型.
1 流动计算和边界层方程求解层流翼型设计的关键是能够准确判断流动发生转捩的位置.通常Reynolds Average Navier-Stokes (RANS) 方程耦合湍流模型不能准确地判断翼型表面的转捩位置,而基于小扰动理论的eN转捩判断方法具有完善的理论基础,能够得到比较准确的转捩位置而被广泛应用,但是需要准确的边界层内速度分布.另一方面,由于翼型优化过程耗时较长,因此节省时间成为转捩位置判断工具选取的标准.耦合Euler方程、边界层方程和线性稳定性方程获得转捩位置的方法需要多次迭代才能获得准确的物面压力分布,才能得到准确的转捩位置;而求解RANS方程只需一次计算就可以得到准确的物面压力分布,再耦合边界层方程和线性稳定性方程迭代只需要极少的时间,因此比求解Euler方程的方法效率高很多.基于以上原因,流场计算采用RANS方程.
精确的边界层速度型分布是eN方法准确预测转捩位置的前提,常用求解边界层的方法主要有求解RANS方程和求解边界层方程两种方法.在RANS方程求解中,如果采用二阶精度的数值格式,边界层内数值粘性和物理粘性量级相当,难以精确求得边界层内速度型;如果利用四阶或者更高阶的数值格式,可以降低误差,但是CPU时间将会大大的增加.相比较而言,如果利用积分形式的边界层方程,求解时引入速度分布函数,在获得较高计算精度的同时不会增加计算时间.所以利用求解边界层方程来获得相对精确的速度型分布.
大量的计算结果表明采用二阶精度计算格式求解耦合湍流模型的RANS方程时,可以得到准确的物面压力分布,因此基于RANS方程的解可以得到准确的边界层外边界的速度分布.然而在跨音速状态下,由于翼型表面出现激波,使得流动不等熵,采用等熵关系求解边界层外边界速度分布会有误差,因此需要通过熵修正得到边界层外边界速度分布,其熵修正过程如下:假设自由流参数为P∞、T∞和M∞,波前边界层外边界的总压P01为
P01/P∞=[1+0.5(γ-1)M∞2]γ/(γ-1).
设波前边界层外边界的静压为P1,则波前边界层外边界的马赫数M1为
P01/P1=[1+0.5(γ-1)×M12]γ/(γ-1).
由激波前后总压关系
P02/P01=[1+2γ(γ+1)-1(M12-1)]1/(1-γ){(γ+1)M12/[(γ-1)M12+2]}γ/(γ-1),
求得波后边界层外边界的总压P02.再次利用等熵关系式求得波后流动参数对应等熵条件下的自由来流静压P′∞,其关系式为P02/P′∞=[1+(γ-1)/2×M∞2]γ/(γ-1),
最后利用P∞和P′∞分别求解激波前后边界层外边界的速度分布.激波前边界层外边界无量纲速度关系为
| $ {{\tilde u}_e}\left( {{x_i}} \right) = \sqrt {1 - \frac{2}{{\gamma - 1}}\frac{1}{{M_\infty ^2}}\left( {\bar p_1^{\left( {\gamma - 1} \right)/\gamma } - 1} \right)} ; $ |
| $ {{\tilde u}_e}\left( {{x_i}} \right) = \sqrt {1 - \frac{2}{{\gamma - 1}}\frac{1}{{M_\infty ^2}}\left( {\bar p_2^{\left( {\gamma - 1} \right)/\gamma } - 1} \right)} , $ |
其中 $\bar p$1=pe/p∞,$\bar p$2=pe/p′∞,pe=pw,pw、 pe分别为物面压力和边界层外边界的压力.$\bar u$e(xi)=ue(xi)/u∞,ue(xi)为边界层外边界处的速度,M∞为来流马赫数,γ=1.4.
为了说明计算边界层外边界速度分布时考虑熵修正的必要性,下面通过两个算例进行验证.其一是跨音速状态下RAE2822翼型的绕流流动,另一个为高超音速下NACA0012翼型绕流流动.图 1(a)和图 1(c)分别为跨音速状态下的弱激波和超音速状态下的强激波压力云图.图 1(b)为等熵和考虑熵修正时求出的RAE2822翼型上下表面在M∞=0.729、迎角α=2.31°、雷诺数Re=1.5×107状态下的边界层外边界无量纲速度分布,图 1(d)为等熵和考虑熵修正时求出的NACA0012翼型上下表面在M∞=3.0、迎角α=0°、雷诺数Re=6.2×107状态下的边界层外边界无量纲速度分布.结果表明当流场中出现较强激波时,相应地穿过激波时的熵增也较大,等熵公式计算得到的边界层外边界速度分布与考虑熵修正时的值相差很大,此时必须考虑熵修正,如图 1(d)所示.但是当激波较弱时,熵变化量较小,相应地引起的边界层外速度变化也是小量,可以不考虑熵修正,如图 1(b)所示.
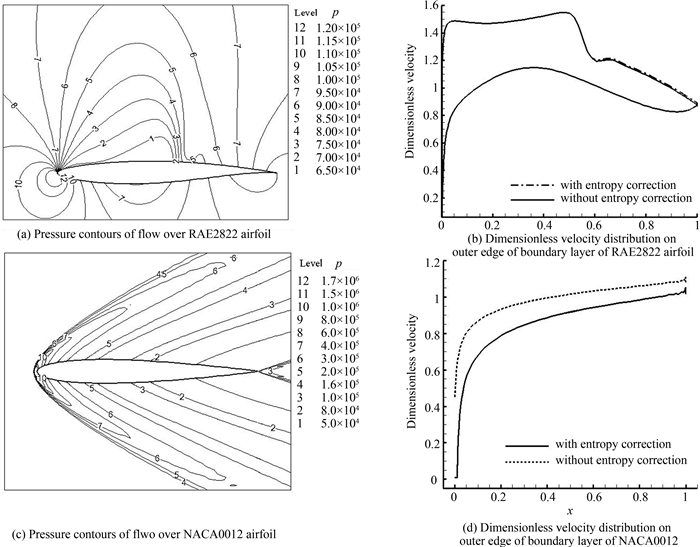 |
| 图1 翼型压力云图和等熵公式与熵修正公式求出的翼型上下表面的无量纲速度分布 Fig. 1 Pressure contours of flow over airfoils and dimensionless velocity distribution of airfoils obtained with isentropic formula and entropy correction formula |
求得边界层外边界的速度分布后,将其作为边界层方程求解的输入,进而求得精确、可靠的边界层内速度型等参数,为线性稳定性方程的求解提供输入[7].
常用的求解边界层方程的方法有Crank-Nicolson方法和Keller的“box”方法,其中Keller的“box”方法更为常用.基于边界层外边界速度分布,使用中心差分格式Keller方法离散曲线坐标系下的边界层方程,再利用牛顿法对离散后的方程线性化得到线化方程组,最后采用“块矩阵消去法”求解得到边界层解,边界层内湍流模型选用Cebeci-Smith湍流模型[6, 7].
2 转捩预测方法及算例验证转捩位置的预测一直是流体力学的一个难题,影响流动转捩的主要机理有T-S波不稳定性、横流不稳定性、附着线转捩和高湍流度状况下的旁路转捩[8].本文研究翼型的自然转捩,高湍流度情况下的旁路转捩和三维效应引起的附着线转捩、横流不稳定性不在研究范围内.
2.1 线性稳定性理论eN方法是基于小扰动理论建立起来的转捩判断方法.通过将一个微小的正弦扰动引入到给定的层流流动中,观察这个扰动随着时间的推移是放大还是衰减来判断流动是否发生转捩.如果扰动衰减,就认为流动保持层流状态;如果扰动足够大,则流动就会发生转捩并发展成湍流.
稳定性方程是从可压缩Navier-Stokes (NS)方程导出的,将方程中独立的物理量分解为平均量与扰动量之和 ${q_i} = {{\bar q}_i} + {{\tilde q}_i}$,并进行线化处理,得到可压缩线性扰动方程组,详细推导参考文献[9, 10].
将上一步求解可压缩边界层方程得到的边界层的解作为线性稳定性方程的输入,通过求解线性稳定性方程得到空间扰动放大率,进一步通过eN方法求解得到扰动放大因子.图 2为Blasius流典型的(αr,R)和(ω,R)稳定性关系图.图中描绘了扰动在给定雷诺数下的三种状态:衰减的、中性的和放大的.αi等于零的曲线为中性稳定性曲线,它把流场分成衰减区域和放大区域.中性稳定性曲线上雷诺数最小的点具有特别的意义,因为小于这个值的所有区域均为稳定的区域,这个最小值称为临界雷诺数.
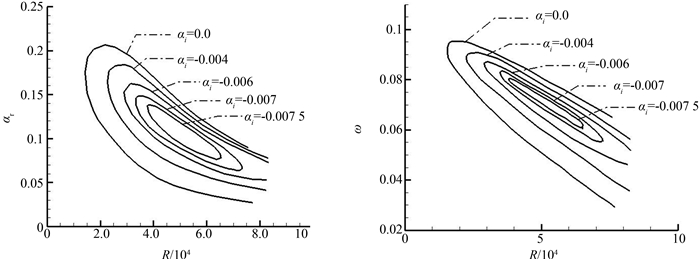 |
| 图2 Blasius流动的稳定性曲线图 Fig. 2 Stability diagram for Blasius flow |
转捩位置的计算起始于中性稳定性曲线下半部分上的一个点,其雷诺数稍大于临界雷诺数.通过求解线性稳定性方程得到不稳定区域内不同频率扰动波在各个位置处的特征值-αi,然后对不同频率的扰动波通过下式积分求得放大因子N,如图 3.依据工程经验取值9作为转捩判断的阈值[7, 11].
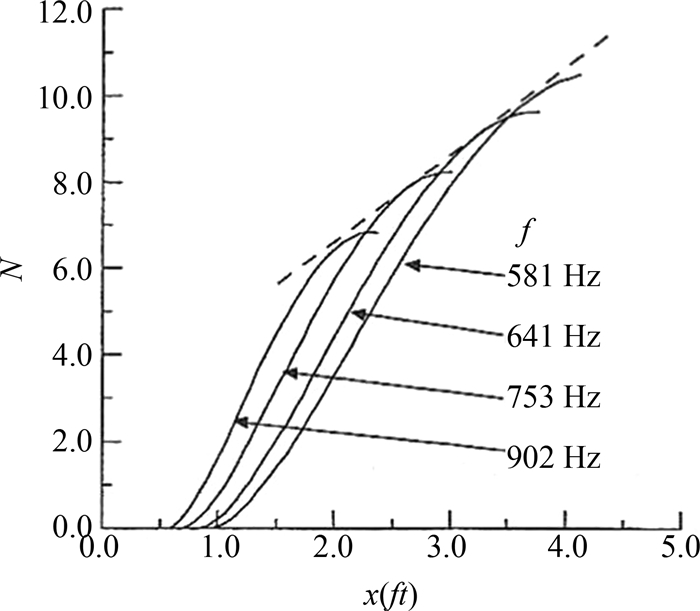 |
| 图3 不同频率扰动的放大因子积分曲线 Fig. 3 Integrated amplification factors as functions of distance at various frequencies |
| $ N = - \int_{{x_0}}^x {{\alpha _i}dx} . $ |
把求解得到的转捩点代入到边界层方程中,再次求解边界层方程,基于得到的边界层内速度分布再次求解线性稳定性方程,进而得到新的转捩位置,然后重复上述过程直到转捩点收敛.
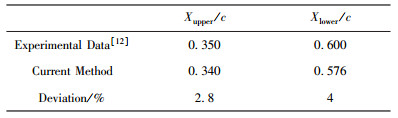
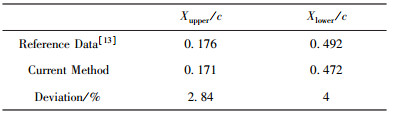
2.2 实例验证选用NLF416翼型和NACA0012翼型作为算例对转捩预测方法进行验证.表 1是NLF416翼型在来流马赫数M∞=0.3、迎角α=2.03°、雷诺数Re=6×106状态下,通过eN方法计算的转捩位置与实验结果[12],表中xupper和xlower分别为翼型上下表面转捩位置.相比于实验值,本方法求解得到的转捩位置略小,但上下翼面误差分别为2.8%和4%,在可接受的范围之内.图 4为NLF416翼型上下翼面不同频率扰动波放大因子积分曲线图.表 2为NACA0012翼型在来流马赫数M∞=0.4、迎角α=2°、雷诺数Re=8×106的状态下,eN方法计算的转捩位置和文献[13]的结果对比.从表中看出本方法计算得到的翼型上下表面转捩位置分别为0.171和0.472弦长,均接近于文献中的值.图 5为NACA0012翼型上下翼面不同频率扰动波放大因子积分曲线图.
| 表1 NLF416翼型转捩位置结果对比 Table 1 Predicted transition locations and experimental result of NLF416 airfoil |
 |
| 点击放大 |
| 表2 NACA0012翼型转捩位置结果对比 Table 2 Predicted transition locations and reference date of NACA0012 airfoil |
 |
| 点击放大 |
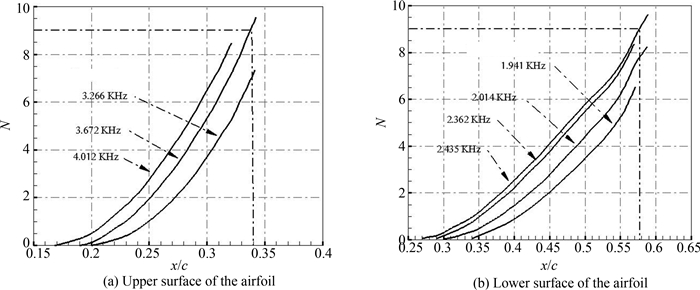 |
| 图4 不同频率扰动的放大因子积分曲线图 Fig. 4 Integrated amplification factors as functions of distance at various frequencies |
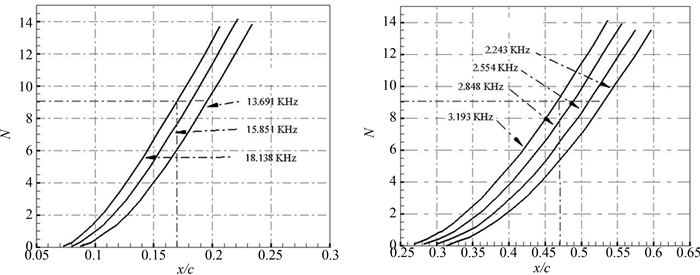 |
| 图5 不同频率扰动的放大因子积分曲线图 Fig. 5 Integrated amplification factors as functions of distance at various frequencies |
通过两组算例发现eN方法计算得到的翼型转捩位置与实验和参考文献结果比较接近,误差在可接受的范围之内,具有较高的准确性,可以作为自然层流翼型设计中转捩判断的依据.
3 层流翼型优化设计及激波控制方法早期层流翼型的设计,很重视提高失稳临界雷诺数.直到上世纪70年代才认识到这个失稳临界雷诺数在决定转捩位置时并非是最重要的.因为转捩是当边界层内的扰动达到一定大小时才发生的,所以边界层内扰动的增长和它们随扰动频率的变化才是更重要的.研究表明在一定的顺压梯度下,尽管失稳点在翼型的前缘附近,但转捩点可能达到70%弦长位置[7, 14].下文利用推迟流动转捩位置进行自然层流翼型优化设计.
3.1 自然层流翼型的优化设计自然层流翼型的设计原则就是推迟流动发生转捩的位置,即
| $ \left\{ \begin{array}{l} \mathop {Max}\limits_y {f_{trans}},\\ y = \left\{ {{y_{1\_up}}, \cdots ,{y_{7\_up}};{y_{1\_low}}, \cdots ,{y_{7\_low}}} \right\}, \end{array} \right. $ |
选用RAE2822翼型为初始翼型,在来流马赫数M∞=0.729,迎角α=2.31°,雷诺数Re=1.5×107状态下,基于单目标遗传算法,以上下翼面转捩位置最大化为优化目标进行层流翼型优化设计,考虑升力约束后的优化问题;
| $ \left\{ \begin{array}{l} \mathop {Max}\limits_y {f_{trans}} = \left( {{x_{upper}} + {x_{lower}}} \right) + \beta \left( {{C_L} - {C_{L0}}} \right)C_{{L_{\rm{0}}}}^{{\rm{ - 1}}}\left( {{x_{upper}} + {x_{lower}}} \right),\\ subject\;\;to:\\ {C_L} \ge {C_{{L_0}}},\;\;\;\beta = 0,\\ {C_L} < {C_{{L_0}}},\;\;\;\;\beta = 1,\\ y = \left\{ {{y_{1\_up}}, \cdots ,{y_{7\_up}};{y_{1\_low}}, \cdots ,{y_{{\rm{7}}\_up}}} \right\}, \end{array} \right. $ |
上式中y1_up,…,y7_up和y1_low,…,y7_low分别为Bezier曲线控制多边形控制点的y坐标,这里为设计变量; CL0为约束升力系数,xupper为翼型上翼面转捩位置,xlower为下翼面转捩位置.翼型优化迭代过程如图 6所示,从图中看出上下翼面转捩位置随着优化代数的增加而增大,约30代时转捩位置基本稳定,达到最优解.从表 3中可以看出优化后翼型的上下翼面的转捩位置推迟了,上翼面从原来的13.6%弦长推迟到59%弦长,下翼面较初始翼型也增加了7%.
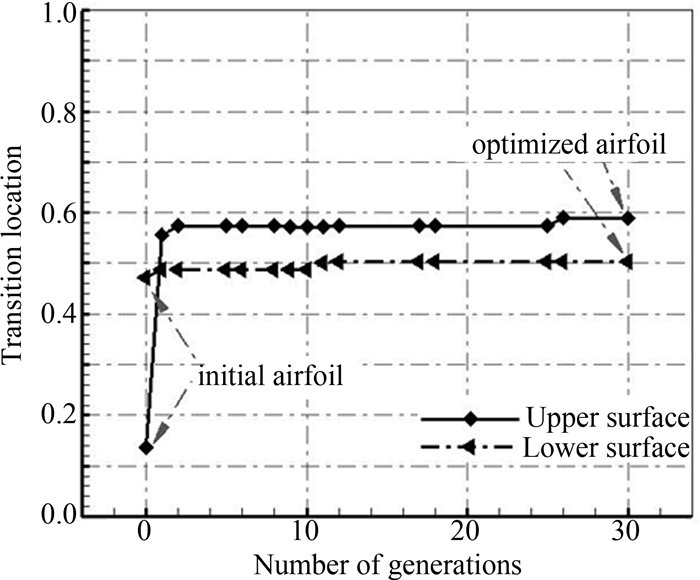 |
| 图6 层流翼型优化历程图 Fig. 6 Convergence history of laminar airfoil optimization |
| 表3 翼型优化前后气动数据对比 Table 3 Aerodynamic performance of RAE2822 airfoil and optimized airfoil |
 |
| 点击放大 |
层流化的目的是为了减阻,但是减阻设计却未必能实现层流化.为此目的,将同样条件下的减阻优化结果和层流设计结果进行了比较.对比图 7(a)中RAE2822翼型、以层流区域最大化为优化目标得到的翼型和以总阻力最小为优化目标得到的翼型的压力分布图和表 3中对应翼型的数据可以得出:以总阻力最小为优化目标得到的翼型的阻力明显减小,但是转捩位置不但没有推迟,反而前移了,所以以总阻力最小为优化目标不能实现层流翼型的优化设计.另一方面,由于摩擦阻力很难通过CFD精确计算,即使以总阻力最小为优化目标得到的优化结果其实际总阻力未必是最小的.相比而言,以转捩位置最大化为优化目标得到的翼型的层流区域明显增加.本文的核心是层流翼型优化设计,所以层流设计就应该以转捩位置作为优化目标.图 7(b)、7(c)和7(d)分别为层流化后得到的翼型、RAE2822翼型和总阻力最小化得到的翼型的压力云图.
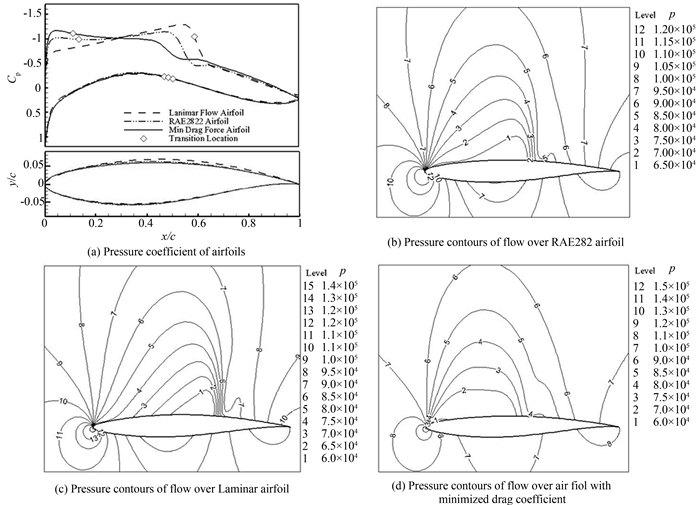 |
| 图7 RAE2822翼型和不同优化目标获得的翼型的表面压力系数分布和压力云图 Fig. 7 Pressure coefficient and pressure contours of flow over airfoils |
从图 7(a)中层流化得到的翼型和初始翼型的压力分布图可以发现,优化后翼型激波强度较初始翼型明显增加,这说明了实现翼面大范围的层流区域,由于顺压梯度的存在必然会产生更强的激波,增加激波阻力,进而消弱层流翼型设计的效果.对比图 7(b)和图 7(c)中层流化翼型和初始翼型的压力云图,同样可以发现层流化得到翼型的激波强度强于初始翼型.因此在层流翼型优化设计的同时有必要寻求一种控制激波强度的方法.
3.2 鼓包减阻优化设计如前所述,在跨音速自然层流翼型的设计过程中,为了推迟转捩位置,就要使得设计翼型上下翼面保持大范围的顺压梯度,这样势必由于翼型后缘驻点的压力恢复,产生较强的激波,在层流翼型设计过程中又不可避免地增加了激波阻力.所以在增加层流区域的同时,也要寻求减小激波阻力的方法.目前有效的激波控制手段有两种:一种是鼓包控制激波技术,如图 8所示,另外一种是后缘调整片技术[15].
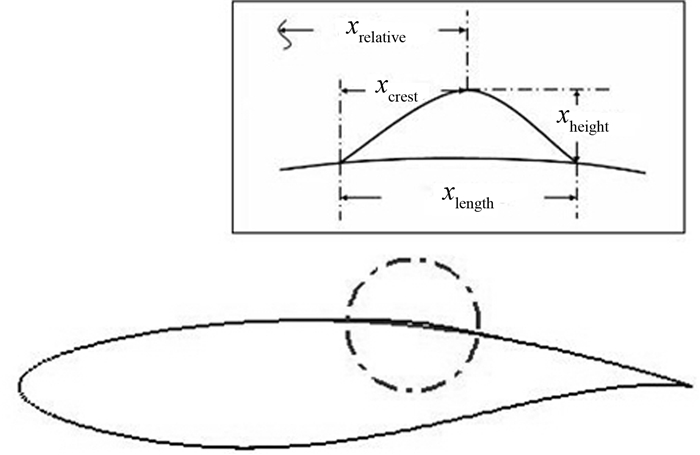 |
| 图8 鼓包示意图 Fig. 8 Schematic diagram of a bump |
鼓包减阻是飞机设计后期提高飞行性能的一种有效技术.其优点是在不改变已有翼型的基础上,增加鼓包装置来控制激波,实现减阻的效果,因此具有很强的应用价值[1, 16].文中利用Hicks-Henne形函数来模拟鼓包的形状[17],其表达式
| $ {Y_k}\left( x \right) = {x_{hei}}{\sin ^3}\left\{ {\pi \left[ {\frac{1}{{{x_{len}}}}\left( {x - {x_{rel}}} \right)} \right]} \right\}, $ |
| $ \left\{ \begin{array}{l} \mathop {Min}\limits_x {C_{Dw}},\\ x = \left\{ {{x_{hei}},{x_{len}},{x_{rel}}} \right\}. \end{array} \right. $ |
应用遗传算法以RAE2822翼型为基准,在来流马赫数M∞=0.729,迎角α=2.31°,雷诺数Re=1.5×107状态下,以激波阻力最小化为优化目标,对鼓包长度、高度和安装位置进行优化.通常波阻很难从压阻(压致阻力)中分离出来,而且跨音速状态下翼型的压阻主要来源于波阻,因此本文直接应用压阻代替波阻作为优化目标进行设计,考虑升力约束后的优化问题:
| $ \left\{ \begin{array}{l} \mathop {Min}\limits_x {f_{{C_D}}} = {C_{{D_p}}} - \beta \left( {{C_L} - {C_{L0}}} \right)C_{L0}^{ - 1}{C_{{D_p}}},\\ subject\;to:\\ {C_L} \ge {C_{L0}},\;\;\beta = 0,\\ {C_L} < {C_{L0}},\;\;\beta = 1,\\ x = \left\{ {{x_{rel}},{x_{hei}},{x_{len}}} \right\}. \end{array} \right. $ |
鼓包优化迭代过程如图 9所示.从图中看出,阻力系数从初始的0.013 2经过优化后下降到0.011 9,翼型的激波强度明显减弱.这也可以从图 10和图 11两个翼型的压力系数曲线图和压力云图中可以看到,加装鼓包优化后翼型的激波强度较初始翼型确有明显减弱,因此鼓包具有控制激波、减小波阻的效果.初始翼型和加装鼓包优化后的翼型气动力系数见表 4.从表中可以得出加装鼓包优化后翼型的气动性能明显得到了改善,升力系数CL增加了2.03%,压致阻力系数CDP减小了9.85%.
| 表4 翼型加装鼓包优化后与初始翼型的气动数据对比 Table 4 Aerodynamic coefficient of airfoil with optimized bump and RAE2822 airfoil |
 |
| 点击放大 |
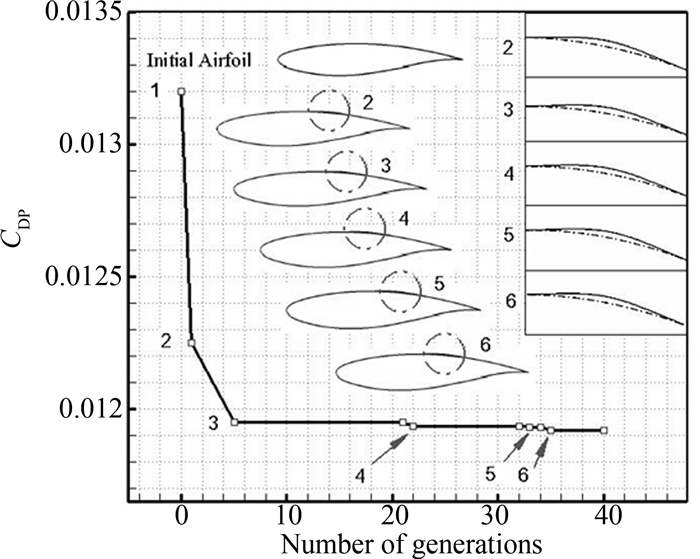 |
| 图9 鼓包优化过程中压致阻力及鼓包形状变化 Fig. 9 Convergence history of bump optimization |
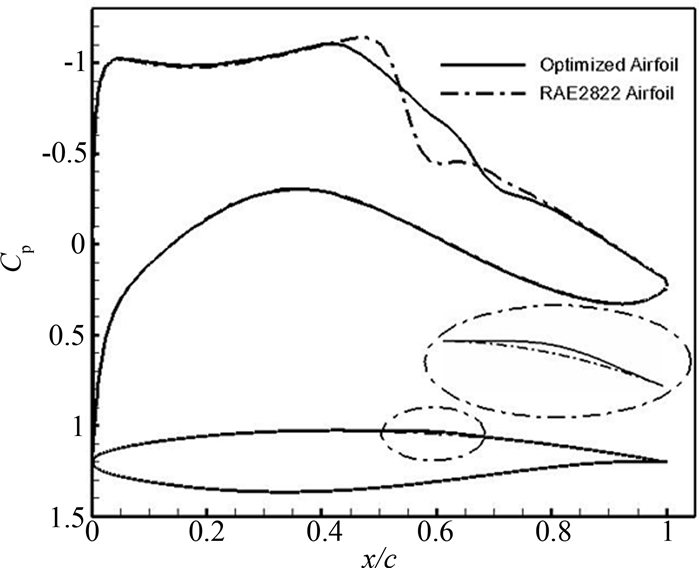 |
| 图10 RAE2822翼型和鼓包优化后翼型压力系数对比 Fig. 10 Pressure coefficients of RAE2822 airfoil and airfoil with optimized bump |
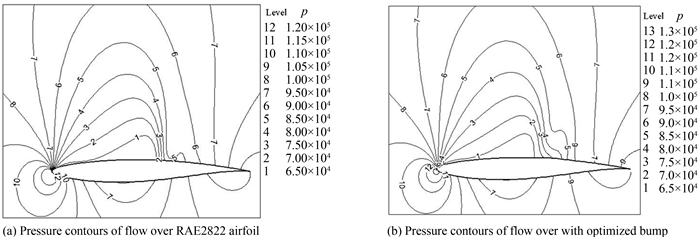 |
| 图11 RAE2822翼型和鼓包优化后翼型的压力云图 Fig. 11 Pressure contours of flow over RAE2822 airfoil and airfoil with optimized bump |
从层流翼型优化设计的结果可以得出,单独进行层流优化设计可以推迟转捩位置,然而由于翼型后缘压力恢复产生较强的激波,明显消弱了层流翼型设计的效果,这就需要对翼型后缘的激波进行控制.另一方面通过对翼型激波位置处加装鼓包并优化鼓包形状确实可以有效地消弱激波强度.为此应用多目标优化方法来解决层流翼型设计过程中转捩位置和激波强度相互矛盾的问题.
4.1 多目标优化方法多目标遗传优化方法其基本原理是模拟达尔文的生物进化论中适者生存和近代生物遗传学机理的计算模型,属于全局搜索最优解的一种方法[18].通常多目标遗传算法有几种常见的处理方式:对不同的目标进行给定的权因子后求和,再对求和的值进行优化;非支配多目标遗传算法;采用Nash均衡的遗传算法等[19].本文使用非支配多目标遗传算法,其流程图见图 12.
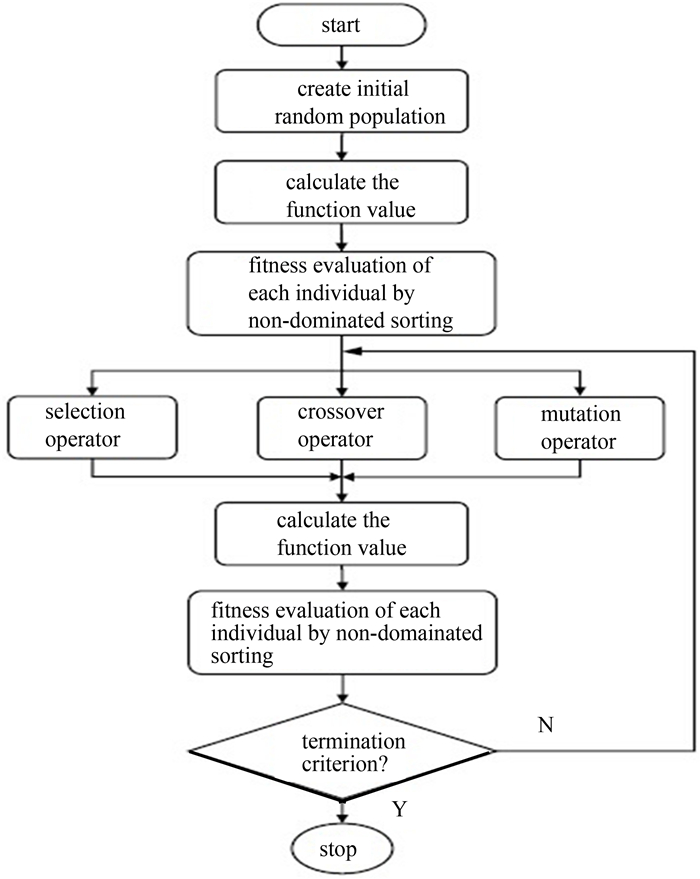 |
| 图12 非支配多目标遗传算法流程图 Fig. 12 Flow chart of non-dominated multi-objective genetic algorithm |
在设计带激波控制的跨音速自然层流翼型的过程中,层流优化的结果是转捩位置的推迟,但是激波阻力也随之增加,所以总阻力不一定有效的减小.因此在层流优化过程中,激波控制是多目标优化的另一个重点和难点.层流翼型设计过程中需要解决的问题有:1) 翼型表面实现大面积的层流区域,即推迟流动转捩的发生;2) 减小后缘由于压力恢复而产生的激波.因此优化问题可以概括为
| $ \left\{ \begin{array}{l} \mathop {Max}\limits_{\left( {x,y} \right)} {f_{trans}},\\ \mathop {Min}\limits_{\left( {x,y} \right)} {f_{{C_D}}},\\ x = \left\{ {{x_{rel}},{x_{len}},{x_{hei}}} \right\}\\ y = \left\{ {{y_{1\_up}}, \cdots ,{y_{7\_up}};{y_{7\_low}}, \cdots ,{y_{7\_low}}} \right\}. \end{array} \right. $ |
以RAE2822翼型为初始翼型,以层流区域最大化和激波阻力最小化为优化目标,应用多目标优化方法,在马赫数M∞=0.729,迎角α=2.31°,雷诺数Re=1.5×107的状态下进行优化设计,考虑升力约束后的优化问题如下:
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{\left( {x,y} \right)} {f_{Trans}} = \left( {{x_{upper}} + {x_{lower}}} \right) + \beta \left( {{C_L} - {C_{L0}}} \right)C_{L0}^{ - 1}\left( {{x_{upper}} + {x_{lower}}} \right),\\ \mathop {\min }\limits_{\left( {x,y} \right)} {f_{{C_D}}} = 30\left[ {{C_{{D_p}}} - \beta \left( {{C_L} - {C_{L0}}} \right)C_{L0}^{ - 1}{C_{{D_p}}}} \right],\\ Subject\;\;to:\\ {C_L} \ge {C_{{L_0}}},\;\;\;\beta = 0,\\ {C_L} < {C_{{L_0}}},\;\;\;\beta = 1,\\ x = \left\{ {{x_{rel}},{x_{len}},{x_{hei}}} \right\},\\ y = \left\{ {{y_{1\_up}}, \cdots ,{y_{7\_up}};{y_{1\_low}}, \cdots ,{y_{7\_low}}} \right\}. \end{array} \right. $ |
在优化过程中,翼型的形状由初始翼型附加Bezier曲线来控制,即Y=YIni+ΔY.其中YIni为初始翼型坐标值,ΔY为Bezier函数拟合的曲线[20].式中
| $ \Delta Y = P\left( t \right)\sum\limits_{i = 0}^n {{P_i}{B_{i,n}}\left( t \right),0 \le t \le 1.} $ |
上式中,Pi为各顶点的位置向量,Bi,n(t)为伯恩斯基多项式.Bezier曲线参数和鼓包参数及变化范围参见图 13和表 5、6.图 14为多目标优化流程图.
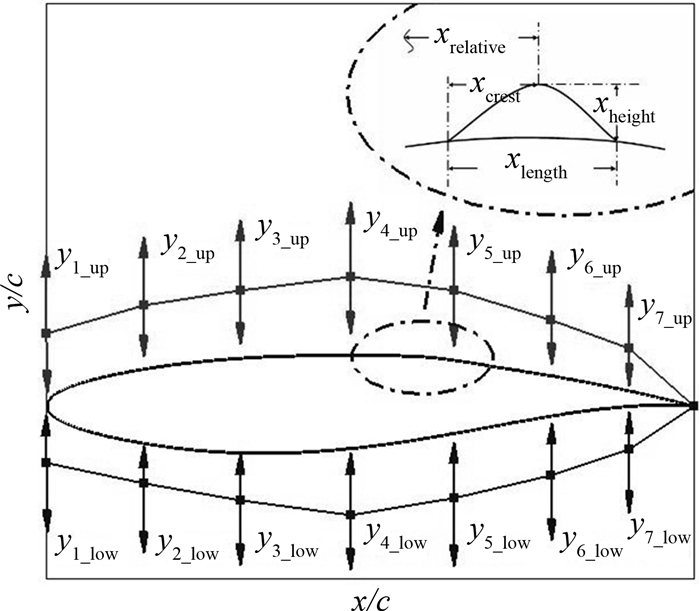 |
| 图13 翼型和鼓包设计变量示意图 Fig. 13 Schematic diagram of design variables of airfoil and bump |
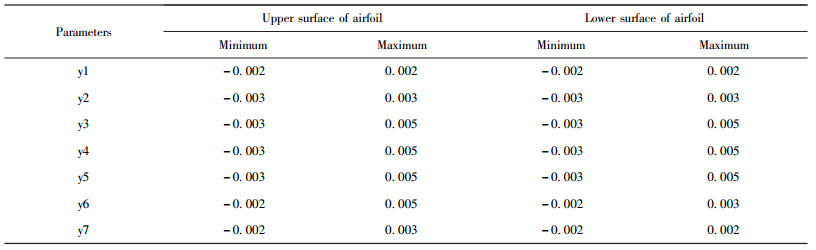
| 表5 翼型参数取值范围 Table 5 Search space of airfoil parameters |
 |
| 点击放大 |
| 表6 鼓包参数取值范围 Table 6 Search space of bump parameters |
 |
| 点击放大 |
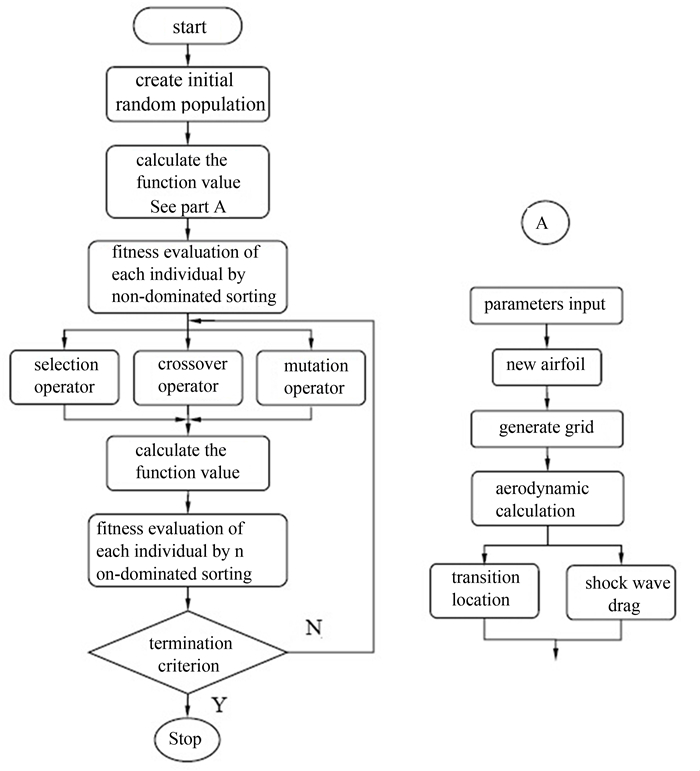 |
| 图14 多目标优化流程图 Fig. 14 Diagram of multi-objective optimization |
经过优化后得到该多目标问题的Pareto阵面,见图 15,其上一系列的点给出了翼型气动性能的变化趋势:阵面上,随着翼型转捩位置的推迟,翼型的激波阻力也随之增强;层流区域最大的翼型,其激波强度明显强于别的翼型;阵面上对应的所有翼型其层流区域及激波强度相比初始翼型均有所改善.在跨音速状态下,由于超临界翼型上表面中段比较平坦,激波不易稳定存在于此区域,转捩有可能发生在失稳点附近,即压力最低点或者激波位置处,所以Pareto阵面中间出现不连续的情况.
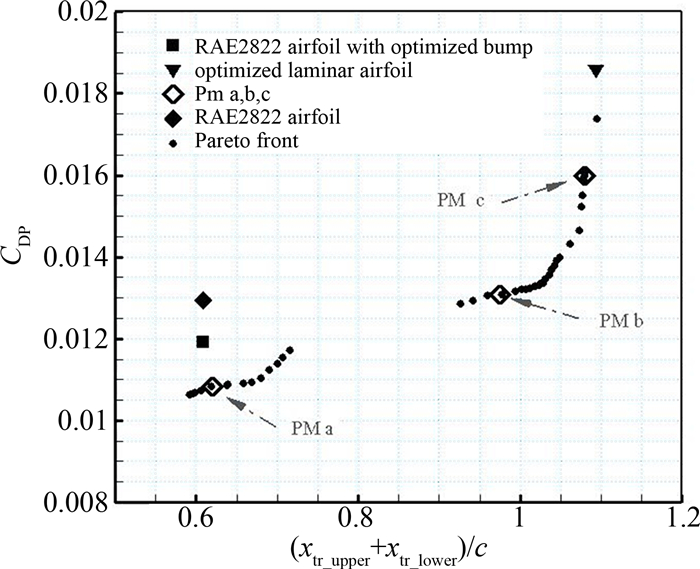 |
| 图15 Pareto阵面 Fig. 15 Pareto front |
由于单独鼓包优化过程中调整的只是鼓包参数,而多目标优化过程中翼型参数和鼓包参数同时影响翼型的压力分布及激波强度.因此,改变翼型和鼓包参数的多目标优化设计对激波的控制优于单独鼓包优化的翼型.所以,单独鼓包优化得到的翼型不在Pareto阵面上.
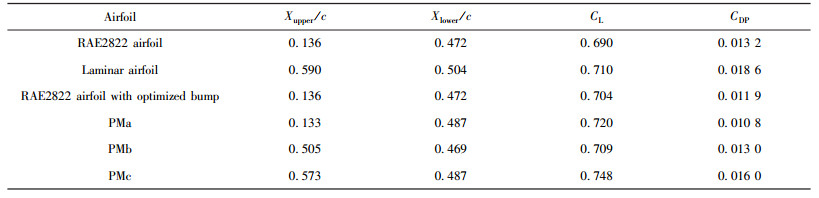
表 7中为初始翼型、RAE2822翼型、带优化后鼓包的RAE2822翼型、优化后层流翼型和阵面上PMa (Pareto Member a)、PMb和PMc三个翼型的气动数据对比,图 15为初始翼型和Pareto阵面上翼型以及分别单独优化鼓包和单独层流设计后翼型的气动性能对比.从图(表)中发现单独鼓包优化后,翼型的激波有所减弱,但是转捩位置仍然在翼型的前缘,翼型表面仍然为湍流流动,所以翼型的摩擦阻力仍旧很大.而单独层流优化得到的翼型,其转捩位置大大推迟,从初始翼型的13.6%弦长推迟到60%弦长,但是翼型的激波强度也增大近40%,明显大于初始翼型,这就消弱了层流翼型优化设计的效果.相比之下,Pareto阵面上翼型的转捩位置及激波强度明显优于初始翼型,阵面上左下缘对应翼型的激波强度较初始翼型减小约18%,右上缘对应翼型的转捩位置由初始翼型的13.6%增加到约57%弦长,而阵面上中部对应翼型的转捩位置推迟到50%弦长,而激波强度几乎没有增加.图 16为阵面上PMa、PMb和PMc三个翼型与初始翼型的压力系数和转捩位置对比图,图 17为阵面上PMa、PMb和PMc三个翼型的压力云图,这些图更为清晰的证明了上面的结论.综上所述,Pareto阵面上翼型的总体性能较初始翼型均有明显改善.
| 表7 阵面上PMa、PMb和PMc翼型与初始翼型、单独鼓包优化后翼型和单独层流优化后翼型的气动数据 Table 7 Aerodynamic performance of airfoils |
 |
| 点击放大 |
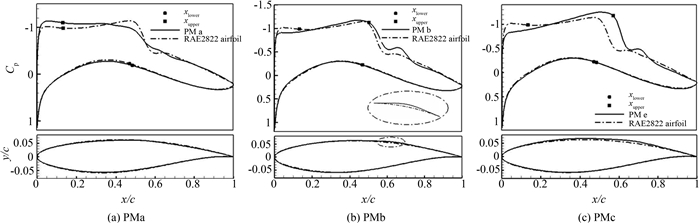 |
| 图16 翼型的压力系数及转捩位置对比 Fig. 16 Pressure coefficients and transition locations of different airfoils |
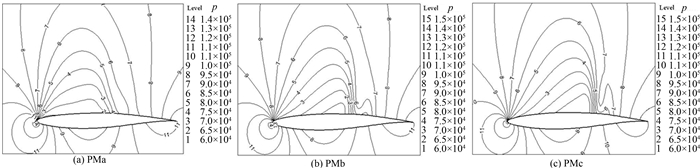 |
| 图17 Pareto阵面上翼型的压力云图 Fig. 17 Pressure contours of flow over airfoils on the Pareto front |
利用求解RANS方程和边界层方程得到边界层内的速度分布、位移厚度、动量厚度等,然后求解可压缩线性稳定性方程,积分得到空间扰动放大率,以此方法作为转捩位置判断的准则,并通过NLF416和NACA0012翼型验证本方法的准确性,结果证明此方法能够比较准确的预测流动的转捩,可以作为翼型转捩预测的方法.
跨音速自然层流翼型的设计需要保持翼面上大范围的顺压梯度,随着顺压梯度区域的增大,在翼型后缘由于压力恢复,必将产生更强的激波,不可避免地增加了激波阻力.为减弱翼型的激波强度,利用鼓包控制激波的方法弱化激波,达到减小激波阻力的目的.
通过分析分别以转捩位置最大和总阻力最小为优化目标得到的翼型的气动性能得出:以总阻力最小为优化目标得到的翼型并不一定能扩大层流区域,因此采用转捩位置最大化作为优化目标进行层流设计.
通过分析得到层流翼型设计的可行性、鼓包控制激波的可行性之后,基于多目标优化方法从RAE2822翼型出发,以翼面层流区域最大化和激波阻力最小化为设计目标,设计出了带激波控制的跨音速自然层流翼型.得到了该多目标问题的Pareto阵面解,通过对阵面上翼型与初始翼型的气动性能对比分析得到:优化后翼型的层流区域和激波强度较初始翼型均有所改善;其性能明显优于单独层流或者单独鼓包获得的翼型.同时也证明了本文发展的多目标优化方法是可行的,可以有效地解决层流翼型优化设计过程中转捩位置和激波强度之间的矛盾
| [1] | JONE E G. Laminar flow control-back to future[R]. AIAA-2008-3738. American Institute of Aeronautics and Astronautics, 2008:1-23. |
| [2] | RENEAUX J. Overview on drag reduction technologies for civil transport aircraft[C]//Rossi T. European Congress on Computational Methods in Applied Science and Engineering. France:ONERA, 2004:2-13. |
| [3] | PETER S. An aerodynamic design method for supersonic natural laminar flow aircraft[D]. Stanford:Department of Aeronautics and Astronautics, 2004. |
| [4] | ZHU Z Q, WU Z C, DING J C. Laminar flow control technology and application[J]. Acta Aeronautics et Astronautics Sinica, 2011, 32(5):765-784. |
| [5] | JOSLIN R D. Overview of laminar flow control[R]. NASA TP-1998-208705. Langley Research Center, 1998:3-28. |
| [6] | CEBECI T, KAUPS K, JUDY A R. A general method for calculating three dimensional compressible laminar and turbulent boundary layers on arbitrary wings[R]. NASA CR-2777, Langley Research Center, 1977:1-8. |
| [7] | CEBECI T, COUSTEIX J. Modeling and computation of boundary layer flow:laminar, turbulent and transitional boundary layers in compressible flows[M]. Long Beach:Horizons Publishing, 2003:58-230. |
| [8] | DONG M. A study on the mechanism of bypass transition[J]. Physics of Gases, 2012, 7(4):21-29. |
| [9] | CHEN L. Studies of vortical structures and transition mechanisms in transitional boundary layers[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2010. |
| [10] | 王博. 二维可压缩流动转捩计算[D]. 西安:西北工业大学, 2004. |
| [11] | KRUMBEIN A. Automatic transition prediction and application to the high-lift multi-element configurations[J].Journal of Aircraft, 2005, 42(5):1150-1164. |
| [12] | JEN D L, A JAMESON. Natural-laminar-flow airfoil and wing design by adjoint method and automatic transition prediction[R]. AIAA-2009-897. American Institute of Aeronautics and Astronautics, 2009:1-5. |
| [13] | DRIVER J, ZINGGY D W. Optimized natural-laminar-flow airfoils[J]. AIAA Journal, 2002, 40(6):4-6. |
| [14] | LUO J S, LU C G, ZHOU H. A numerical investigation for the propagation velocity of small amplitude disturbance in the problem of hydrodynamic stability[J]. Acta Aerodynamica Sinica, 2002, 20(1):1-8. |
| [15] | COUSTOLS E, PAILHAS G, SAUVAGE P. Scrutinising flow field pattern around thick cambered trailing edges:experiments and computations[J]. International Journal of Heat and Fluid Flow, 2000, 21(3):264-270. |
| [16] | PATZOLD M. Numerical optimization of finite shock control Bumps[R]. AIAA 2006-1054. American Institute of Aeronautics and Astronautics, 2006:2-4. |
| [17] | ZHONG X P, DING J F, LI W J. Robust Airfoil optimization with multi-objective estimation of distribution algorithm[J]. Chinese Journal of Aeronautics, 2008, 21(4):289-295. |
| [18] | DEVILLER J. Genetic algorithm in molecular modeling[M]. London:Academic Press, 1996:25-136. |
| [19] | TANG Z L, DONG J. On coupling in multi-criterion aerodynamic design optimization problems using adjoint methods and game strategies[J]. Chinese Journal of Aeronautics, 2009, 22(1):1-8. |
| [20] | 陈元琰, 张睿哲, 吴东. 计算机图形学实用技术[M]. 北京:清华大学出版社, 2007:167-173. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
