0 引言

在实际工程问题中，流场中经常会同时出现可压缩与不可压缩区域同时存在的问题，发展能够快速、准确地求解这类流动问题的计算流体力学(CFD)数值算法成为工程应用必然的要求.

随着CFD算法研究的不断深入，通过求解可压缩Euler方程或者Navier-Stokes方程模拟流动过程的方法，在亚跨声速、超声速及高超声速流动的数值分析中已经取得广泛的应用.为了求解这类偏微分方程并准确反映其背后的不同物理过程，提出了一系列数值通量离散方法，如Roe格式^[1]、AUSM类格式^{[2, 3, 4, 5]}、CUSP类格式^{[6, 7]}等.1983年，Harten^[8]提出了一种迎风Godunov类型的迎风HLL格式，经不断改进形成了满足非线性差分方程所要求的稳定性条件、熵条件及正守恒条件的HLLEW格式^{[9, 10, 11, 12]}.HLLEW格式因其较强的非线性处理能力及良好的计算稳定性，在可压缩流动的数值模拟中得到广泛的应用^{[13, 14, 15]}.

虽然在可压缩流动的数值模拟上取得巨大的成功，对于低速流动的模拟，包括HLLEW格式在内的一般的迎风格式并不适用^[16]：一方面，迎风格式的数值粘性大多根据系统的特征值构造，低速流动中由于声速远大于流动速度，这将引起过大的数值耗散，降低对问题的求解精度；另一方面，由特征线理论可以知道，扰动在理想气体的等熵流动中的传播速度为系统的特征值，对于低速流动而言不同方向扰动传播速度相差很大，即所求解的线性方程组的条件数很大，由此引起收敛变慢、求解效率减低的问题.受Chorin^[17]的虚拟压缩方法启发，Turkel^[18]提出了用可压缩方程求解低速流场的预处理方法：通过改变方程的时间导数，使控制方程的各特征速度保持在同量级，从而有效提高对低速流动的求解精度及求解效率.

我们在可压缩Navier-Stokes方程中引入低速预处理技术，重新构造HLLEW格式的耗散项，推导出适用于全速域流场模拟的预处理HLLEW格式.并根据预处理后的雅克比矩阵，基于LU-SGS方法构造隐式时间推进方程.通过对NACA 4412翼型的低速绕流及RAE 2822翼型的跨声速绕流问题的模拟，验证所发展的方法对可压缩及不可压缩流动的处理能力.

1 数值求解方法 1.1 控制方程

在贴体曲线坐标系下的Navier-Stokes方程组的时间导数项前面乘以预处理矩阵Γ，便可得到求解定常流动的预处理控制方程组

$ \Gamma \frac{\partial \hat{W}}{\partial t}+\frac{\partial \hat{E}}{\partial \xi }+\frac{\partial \hat{F}}{\partial \eta }+\frac{\partial \hat{G}}{\partial \xi }\text{=}\frac{\partial {{{\hat{E}}}_{v}}}{\partial \xi }+\frac{\partial {{{\hat{F}}}_{v}}}{\partial \eta }+\frac{\partial {{{\hat{G}}}_{v}}}{\partial \zeta }, $

(1)

其中 $\hat{W}$=(p u v w T)^T，根据原始变量 $\hat{W}$形式的不同预处理矩阵有不同的形式^{[19, 20, 21, 22]}.采用Weiss-Smith^[22]提出的预处理矩阵，该方式处理的控制方程除了在驻点会产生奇异外，不存在声速点奇异和外部边界敏感等不稳定因素，因此具有更好的计算稳定性.Weiss-Smith预处理矩阵

$ \Gamma =\left( \begin{matrix} \Theta & 0 & 0 & 0 & {{\rho }_{T}} \\ {{\Theta }_{u}} & \rho & 0 & 0 & {{\rho }_{T}}u \\ {{\Theta }_{v}} & 0 & \rho & 0 & {{\rho }_{T}}v \\ {{\Theta }_{w}} & 0 & 0 & \rho & {{\rho }_{T}}w \\ \Theta H-1 & \rho u & \rho v & \rho w & {{\rho }_{T}}H+\rho {{C}_{p}} \\ \end{matrix} \right), $

其中，${{\rho }_{T}}=\frac{\partial \rho }{\partial T}\left| _{p} \right.$，$\Theta =\left( \frac{1}{U_{r}^{2}}-\frac{{{\rho }_{T}}}{\rho {{C}_{p}}} \right)$，U_r称为参考速度，本文中参考速度按照以下计算得到

$ {{U}_{r}}={{M}_{r}}c, $

(2)

$ {{M}_{r}}=\min \left( 1,\max \left( k{{M}_{\infty }},M \right) \right), $

(3)

式(2)、(3)中，c为声速，M为流场的当地马赫数，M_∞为无穷远来流马赫数.k为常数，通过调节k的大小可以避免驻点附近的奇异问题，文中统一取k=0.5.

预处理控制方程雅克比矩阵的特征值

$ \lambda \left( {{\Gamma }^{-1}}\frac{\partial \hat{H}}{\partial \hat{W}} \right)=U,U,U,U'-C',U'+C', $

(4)

其中，

$ \begin{align} & U={{n}_{x}}u,+{{n}_{y}}v+{{n}_{z}}w, \\ & U'=\frac{1}{2}U\left( 1+M_{r}^{2} \right), \\ & C'=\frac{1}{2}\sqrt{{{\left( 1-M_{r}^{2} \right)}^{2}}{{U}^{2}}+4M_{r}^{2}{{C}^{2}},} \\ & C=c\sqrt{n_{x}^{2}+n_{y}^{2},+n_{z}^{2}}, \\ \end{align} $

${\hat{H}}$代表无粘通量，n=(n_x,n_y,n_z)为界面的法线方向.

预处理改变了控制方程和声速有关的两个特征值的形式，从而起到调节不同方向扰动传播速度的效果.当流动速度为超声速时，参考马赫数M_r=1，特征值与可压缩流动控制方程的特征值恢复一致；在低速区域M_r→0，预处理方程的特征值大小与U为同一量级.因此，对于不同流速的流动预处理方程的条件数能保持在合理的范围内.

1.2 预处理HLLEW格式

预处理控制方程中，无粘通量采用可压缩流动中得到成功应用的HLLEW格式^{[9, 12]}.与Roe格式一样，HLLEW格式属于Godunov类型迎风格式的一种.相对Roe格式^[1]来讲，在流动连续区域HLLEW格式退化为Roe格式，在间断处HLLEW格式提高了对接触间断的分辨能力，同时可以避免解的非物理震荡和过高的人工粘性，在跨声速流场分析中得到广泛应用.

HLLEW格式根据系统的特征值构造耗散项，在低速流动中由于声速远大于流动速度，这将引起不符合实际物理过程的过大的数值耗散.在预处理方程中，需要相应地改变HLLEW格式的耗散项，以满足对低速流动的流场模拟的需求.

以ξ方向为例，HLLEW格式的数值通量可以写为

$ {{{\hat{E}}}_{i\text{+}1/2,j,k}}=\frac{1}{2}\left( {{{\hat{E}}}_{i,j,k}}+{{{\hat{E}}}_{i+1,j,k}} \right)-\frac{1}{2}{{\left| {\tilde{A}} \right|}_{i+1/2,j,k}}\left( {{{\hat{Q}}}_{i+1,j,k}}-{{{\hat{Q}}}_{i,j,k}} \right), $

(5)

这里 ${\hat{Q}}$=(ρ ρu ρv ρw ρE)^T为守恒变量,${\tilde{A}}$为无粘通量的雅克比矩阵.预处理的HLLEW格式需要改变它粘性项的形式，具体形式

$ \left| {\tilde{A}} \right|\Delta \tilde{Q}\approx \tilde{A}\Delta \tilde{Q}=\Gamma {{\Gamma }^{-1}}\frac{\partial \hat{E}}{\partial \hat{Q}}\Delta \hat{Q}=\Gamma \left( {{\Gamma }^{-1}}\frac{\partial \hat{E}}{\partial \hat{W}} \right)\Delta \hat{W}\approx \Gamma \left| {{{\tilde{A}}}_{\Gamma }} \right|\Delta \tilde{W}=\Gamma \left( \tilde{T}\left| {{{\tilde{\Lambda }}}_{\Gamma }} \right|{{{\tilde{T}}}^{-1}}\Delta \tilde{W} \right), $

(6)

其中，${{{\tilde{A}}}_{\Gamma }}=\partial \hat{E}/\partial \hat{W}$，是预处理方程的雅克比矩阵，Λ=diag(U,U,U,U′-C′,U′+C′)是预处理雅克比矩阵的特征值，${\tilde{T}}$和${\tilde{T}}$^－1分别是预处理方程雅克比矩阵的左右特征向量矩阵，雅克比矩阵及特征向量矩阵的具体形式参见附录A及附录B.b_R⁺和b_L^－反映流场中波传播速度

b_R⁺=max(U′+C′,U′_R+C′_R,0)，

b_L^－=min(U′－C′,U′_R－C′_R,0).

为了降低格式的数值耗散，提高接触间断处的分辨能力，对系统的特征值作以下改动

$ {{{\bar{\Lambda }}}_{\Gamma }}=\frac{b_{R}^{+}+b_{L}^{-}}{b_{R}^{+}-b_{L}^{-}}\Lambda -2\frac{b_{R}^{+}b_{L}^{-}}{b_{R}^{+}-b_{L}^{-}}I. $

(7)

$ {{{\bar{\Lambda }}}_{\Gamma }}=diag\left[ {{{\bar{\lambda }}}_{1}}-2\delta \min \left( b_{R}^{+},b_{L}^{-} \right),{{{\bar{\lambda }}}_{2}}-2\delta \min \left( b_{R}^{+},b_{L}^{-} \right),{{{\bar{\lambda }}}_{\text{3}}}-2\delta \min \left( b_{R}^{+},b_{L}^{-} \right),{{\lambda }_{\text{4}}},{{\lambda }_{\text{5}}} \right], $

(8)

其中

$ \begin{align} & \delta =\min \left( \frac{{{{\tilde{\rho }}}_{1}}}{\left| {{\sigma }_{1}} \right|},\frac{1}{2} \right) \\ & {{\sigma }_{1}}=\Delta \rho -\frac{\Delta p}{{{{\tilde{c}}}^{2}}}. \\ \end{align} $

上述格式，满足非线性差分方程所要求的稳定性条件、熵条件及正守恒条件，具有良好的计算稳定性.通过对系统特征值的修改，HLLEW格式避免了低速流动中过大的数值耗散，适合应用于对低速流动的数值分析.

2 隐式时间推进方法

Yoon和Jameson提出的LU-SGS方法是目前应用比较广泛的隐式时间推进方法.该方法通过简化正负特征矩阵分裂，使得构造的L、U矩阵不包含矩阵求逆，大大提高计算效率.

从控制方程(1)出发，将时间微分项采用一阶近似，对无粘通量采用隐式离散，粘性通量采用显式离散，得到半离散控制方程

$ {{\Gamma }_{i,j,k}}\frac{\hat{W}_{i,j,k}^{n+1}-\hat{W}_{i,j,k}^{n}}{\Delta \tau }+\delta \left( \hat{E}+\hat{F}+\hat{G} \right)_{i,j,k}^{n+1}=\delta \left( {{{\hat{E}}}_{v}}+{{{\hat{F}}}_{v}}+{{{\hat{G}}}_{v}} \right)_{i,j,k}^{n}. $

(9)

对无粘通量做线性化处理，略去二阶及更高阶项有

$ \begin{align} & \frac{{{\Gamma }_{i,j,k}}}{\Delta \tau }\Delta \hat{W}_{i,j,k}^{n}+{{\delta }_{\xi }}\left( \hat{E}+{{A}_{\Gamma }}\Delta \hat{W} \right)_{i,j,k}^{n}+{{\delta }_{\eta }}\left( \hat{F}+{{B}_{\Gamma }}\Delta \hat{W} \right)_{i,j,k}^{n} \\ & \ \ \ \ \ \ \ \ \ \ \ \ +{{\delta }_{\zeta }}\left( \hat{G}+{{C}_{\Gamma }}\Delta \hat{W} \right)_{i,j,k}^{n}=\delta \left( {{{\hat{E}}}_{v}}+{{{\hat{F}}}_{v}}+{{{\hat{G}}}_{v}} \right)_{i,j,k}^{n} \\ \end{align} $

整理后，有

$ \begin{align} & \frac{\Gamma _{i,j,k}^{n}}{\Delta t}\Delta \hat{W}_{i,j,k}^{n}+\left( {{A}_{\Gamma }}\Delta \hat{W} \right)_{i+1/2,j,k}^{n}-\left( {{A}_{\Gamma }}\Delta \hat{W} \right)_{i-1/2,j,k}^{n}+\left( {{B}_{\Gamma }}\Delta \hat{W} \right)_{i,j+1/2,k}^{n}-, \\ & \left( {{B}_{\Gamma }}\Delta \hat{W} \right)_{i,j-1/2,k}^{n}+\left( {{C}_{\Gamma }}\Delta \hat{W} \right)_{i,j,k+1/2}^{n}-\left( {{C}_{\Gamma }}\Delta \hat{W} \right)_{i,j,k\text{-1/2}}^{n}=-\hat{R}_{i,j,k}^{n} \\ \end{align} $

(10)

其中残差 $\hat{R}_{i,j,k}^{n}=\delta \left( \hat{E}+\hat{F}+\hat{G} \right)_{i,j,k}^{n}-\delta \left( {{{\hat{E}}}_{v}}+{{{\hat{F}}}_{v}}+{{{\hat{G}}}_{v}} \right)_{i,j,k}^{n}$，对方程(10)中的雅克比矩阵按照其特征值符号的正负采用迎风分裂，有

$ \begin{align} & {{\left( {{A}_{\Gamma }}\Delta \hat{W} \right)}_{i+1/2,j,k}}=A_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+A_{\Gamma i+1,j,k}^{-}\Delta {{{\hat{W}}}_{i+1,j,k}}, \\ & {{\left( {{A}_{\Gamma }}\Delta \hat{W} \right)}_{i-1/2,j,k}}=A_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+A_{\Gamma i-1,j,k}^{-}\Delta {{{\hat{W}}}_{i-1,j,k}}, \\ & {{\left( {{B}_{\Gamma }}\Delta \hat{W} \right)}_{i+1/2,j,k}}=B_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+B_{\Gamma i,j+1,k}^{-}\Delta {{{\hat{W}}}_{i,j+1,k}}, \\ & {{\left( {{B}_{\Gamma }}\Delta \hat{W} \right)}_{i-1/2,j,k}}=B_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+B_{\Gamma i,j-1,k}^{-}\Delta {{{\hat{W}}}_{i,j-1,k}}, \\ & {{\left( {{C}_{\Gamma }}\Delta \hat{W} \right)}_{i+1/2,j,k}}=C_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+C_{\Gamma i,j,k+1}^{-}\Delta {{{\hat{W}}}_{i,j,k+1}}, \\ & {{\left( {{C}_{\Gamma }}\Delta \hat{W} \right)}_{i-1/2,j,k}}=C_{\Gamma i,j,k}^{+}\Delta {{{\hat{W}}}_{i,j,k}}+C_{\Gamma i,j,k-1}^{-}\Delta {{{\hat{W}}}_{i,j,k-1}}, \\ \end{align} $

代入(10)上式整理，有

$ \begin{align} & \frac{I_{i,j,k}^{n}}{\Delta \tau }+\left( \tilde{A}_{\Gamma i,j,k}^{+}-\tilde{A}_{\Gamma i,j,k}^{-}+\tilde{B}_{\Gamma i,j,k}^{+}-\tilde{B}_{{{\Gamma }_{i,j,k}}}^{-}+\tilde{C}_{\Gamma i,j,k}^{-} \right)]\Delta \hat{W}_{i,j,k}^{n}+ \\ & \left( \tilde{A}_{\Gamma i+1,j,k}^{-}\Delta \hat{W}_{i+1,j,k}^{n}+\tilde{B}_{\Gamma i,j+1,k}^{-}\Delta \hat{W}_{i,j+1,k}^{n}+\tilde{C}_{\Gamma i,j,k+1}^{-}\Delta \hat{W}_{i,j,k+1}^{n} \right)- \\ & \left( \tilde{A}_{\Gamma i-1,j,k}^{-}\Delta \hat{W}_{i-1,j,k}^{n}+\tilde{B}_{\Gamma i,j-1,k}^{-}\Delta \hat{W}_{i,j-1,k}^{n}+\tilde{C}_{\Gamma i,j,k-1}^{-}\Delta \hat{W}_{i,j,k-1}^{n} \right)=-\Gamma _{i,j,k}^{-1}\hat{R}_{i,j,k}^{n}, \\ \end{align} $

(11)

其中，

$ \tilde{A}_{\Gamma }^{\pm }=\frac{1}{2}{{\Gamma }^{-1}}\left( {{A}_{\Gamma }}\pm \chi {{\sigma }_{{{A}_{\Gamma }}}}I \right),\ \tilde{B}_{\Gamma }^{\pm }=\frac{1}{2}{{\Gamma }^{-1}}\left( {{B}_{\Gamma }}\pm \chi {{\sigma }_{{{B}_{\Gamma }}}}I \right),\ \tilde{C}_{\Gamma }^{\pm }=\frac{1}{2}{{\Gamma }^{-1}}\left( {{C}_{\Gamma }}\pm \chi {{\sigma }_{{{C}_{\Gamma }}}}I \right), $

σ_AΓ,σ_BΓ,σ_CΓ为谱半径.对式(11)左端采用近似LU分解，有

$ \left( L+D \right){{D}^{-1}}\left( D+U \right)\Delta \hat{W}_{i,j,k}^{n}=-\Gamma _{i,j,k}^{-1}\hat{R}_{i,j,k}^{n}, $

(12)

其中，

$ \begin{array}{l} L = - \left( {\tilde A_{\Gamma i{\rm{ - 1,}}j,k}^ + + \tilde B_{\Gamma i{\rm{,}}j - 1,k}^ + + \tilde C_{\Gamma i{\rm{,}}j,k - 1}^ + } \right),\\ D = \frac{{{I_{i,j,k}}}}{{\Delta t}} + \chi \left( {{\sigma _{A\Gamma }} + {\sigma _{{\rm B}\Gamma }} + {\sigma _{C\Gamma }}} \right){I_{i,j,k}},\\ U = \left( {\tilde A_{\Gamma i + {\rm{1,}}j,k}^ - + \tilde B_{\Gamma i{\rm{,}}j + {\rm{1}},k}^ - + \tilde C_{\Gamma i{\rm{,}}j,k + {\rm{1}}}^ - } \right). \end{array} $

求解方程(12)，具体推进过程分两步进行

$ \begin{align} & \left( L+D \right)\Delta {{{\hat{W}}}^{*}}=-{{\Gamma }^{-1}}\hat{R} \\ & \left( D+U \right)\Delta \hat{W}=D\Delta {{{\hat{W}}}^{*}}. \\ \end{align} $

(13)

最后更新数值解，得到第n+1时间层守恒变量值

$ \hat W_{i,j,k}^{n + 1} = \hat W_{i,j,k}^n + \Delta {{\hat W}_{i,j,k}}. $

(14)

3 计算结果与讨论

为了验证预处理HLLEW格式对可压缩及不可压缩流动的求解能力与精度，计算NACA 4412二维翼型低速绕流与RAE 2822翼型跨声速绕流问题，计算的马赫数范围从0.01到0.729不等.

3.1 NACA 4412翼型低速绕流

为了考察预处理HLLEW格式对低速不可压缩流动问题的求解能力，计算NACA 4412翼型绕流.计算工况如下：来流马赫数M_∞=0.2，攻角α=13.87°，雷诺数Re=1.52×10⁶.计算网格采用C型结构网格，共分布有96×448个网格单元，其中翼型表面分布256个网格单元，边界层首层网格高度为8×10^－6倍弦长.为了进一步验证本文方法，在同样攻角和雷诺数下，增加了M_∞=0.01工况.在这两个工况的计算中，湍流模型采用k－ω SST两方程模型.

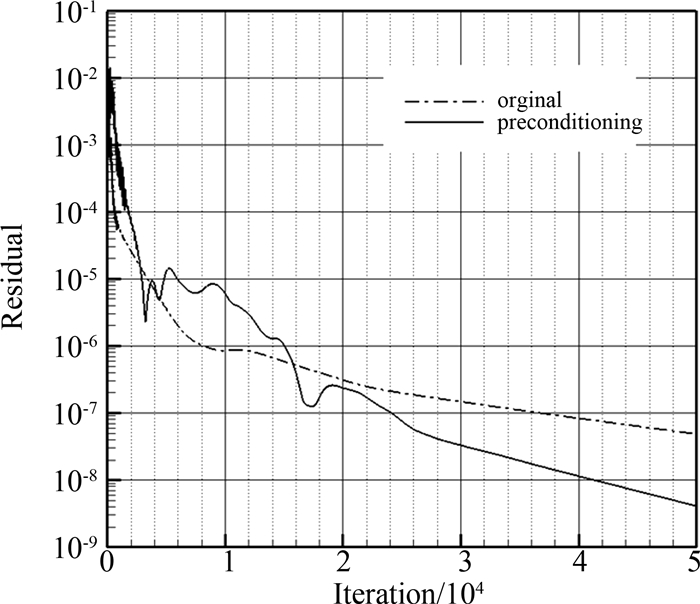
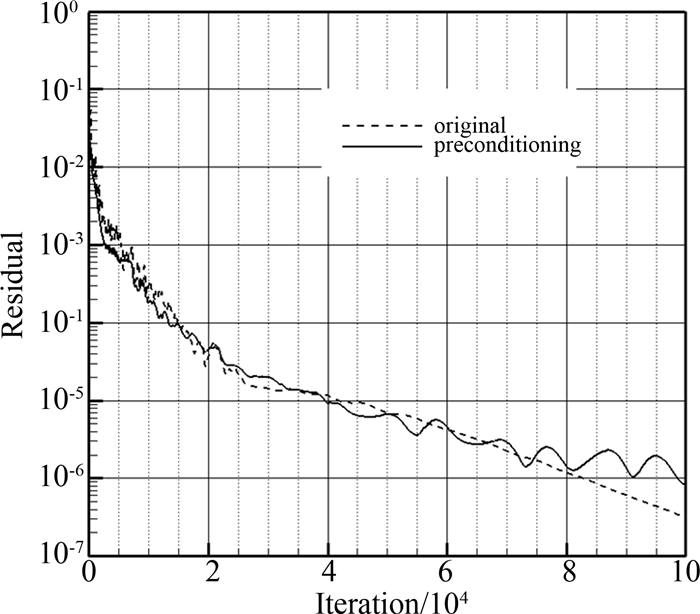
图 1给出了来流马赫数为0.2条件下，预处理方法与原有方法收敛速率的对比.从图中可以看出：相对原始方法，在计算初始阶段预处理方法的残差波动较大，随着计算结果的逐渐收敛，预处理方法的残差波动逐渐消失；从总的计算过程来看，预处理方法的残差下降速度要高于原始方法，说明预处理方法相对原始方法具有更高的收敛速率.

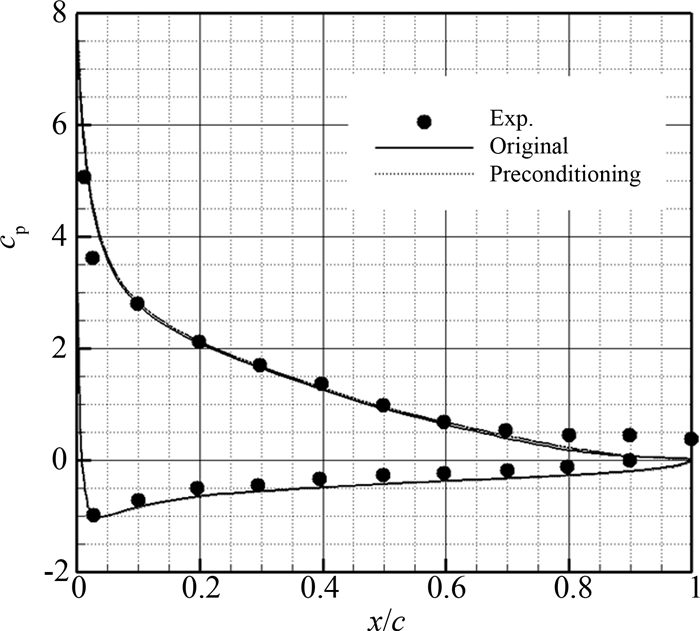
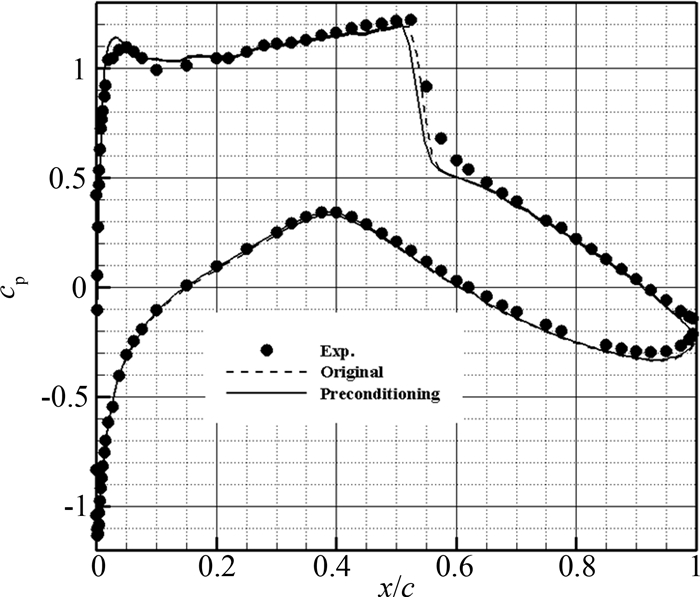
图 2给出了预处理方法和原有方法计算得到的翼型表面压力分布与实验结果^[23]的对比.从图中可以看出，两种方法计算得到的表面压力分布基本一致，与实验结果吻合良好；在后缘的分离区附近，两种方法的计算结果都低估分离区的大小，计算得到后缘上表面的压力系数小于实验值.

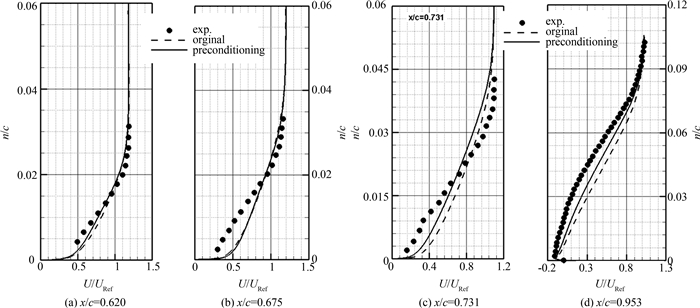
图 3 给出了翼型上表面不同站位上的速度分布与实验结果的对比.从图中可以看出，在上表面分离区之前，两种方法得到的速度分布基本一致；在分离区，预处理方法计算得到的分离强度要大于原有方法，所预测的速度分布更接近实验结果.

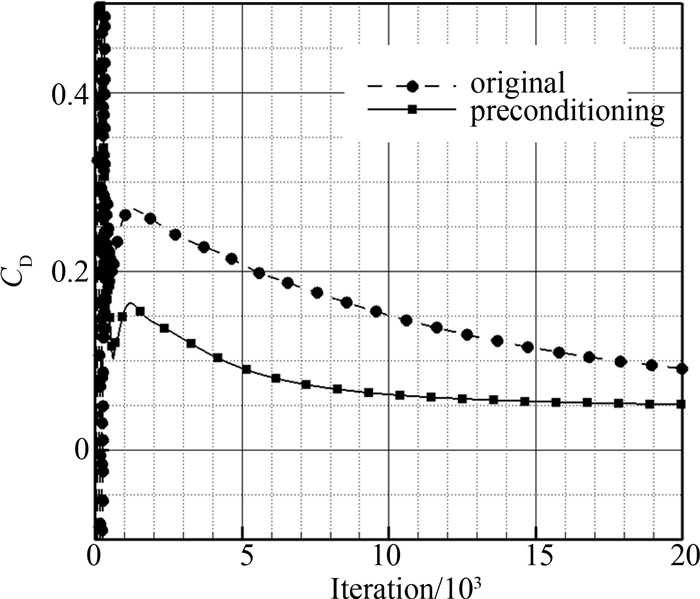
为了进一步对比研究预处理方法与原有方法对低速不可压缩流动问题求解效率，计算了来流马赫数M_∞=0.01的情况，并对比两种方法阻力系数收敛速率.图 4给出了两种方法阻力系数收敛曲线，从图中可以看出：在计算初始阶段，预处理方法的阻力系数的波动程度远小于原有方法；随着计算时间的推进，预处理方法的阻力系数相对原有方法能够更快的收敛.

3.2 RAE 2822跨声速绕流

为了验证预处理方法对跨声速可压缩流动的计算精度，计算了RAE 2822翼型在来流马赫数M_∞=0.729时的定常流动，相对弦长的雷诺数Re=6.5×10⁶，来流攻角α=2.31 °.所求解的雷诺平均Navier-Stokes(RANS)方程中，采用k－ω SST 两方程模型.计算网格采用C型结构网格，共分布有64×368个网格单元，其中翼型表面分布304个网格单元，边界层首层网格高度为1×10^－5倍弦长.

图 5给出了预处理方法和原有方法的残差收敛曲线.从图中可以看出，相对原有方法预处理方法的残差收敛存在一定的波动，总得来说二者的收敛速率基本相当.图 6给出了预处理方法与原有方法计算得到的表面压力分布与实验结果的对比.在流动连续区，预处理方法与原有方法预测的表面压力分布基本一致，都与实验结果吻合良好；在间断处，预处理方法预测的激波位置较原有方法略微靠后，与实验结果略有偏差.

4 结论

引入Weiss-Smith预处理方法，将在可压缩流动中得到广泛应用的HLLEW格式与预处理技术结合，构造适用于全速域流场的数值模拟方法.预处理方法改变系统的特征值大小，降低系统刚性、加快流场的求解效率；通过对HLLEW格式中耗散项的修改，避免不可压缩流动中过大的非物理耗散，提高对低速流动的求解精度.

对NACA 4412低速绕流及RAE 2822跨声速绕流问题的模拟结果表明：低速不可压流动中，预处理方法具有更高的收敛速率和求解精度；在跨声速可压缩流动中，预处理方法的求解能力与原有方法相当.总的来讲，预处理HLLEW方法具有更好的鲁棒性，适合于用于全速域流场的数值模拟.

附录A 雅克比矩阵

$ \begin{array}{l} \Gamma = \left( {\begin{array}{*{20}{c}} \Theta &0&0&0&{{\rho _T}}\\ {\Theta u}&\rho &0&0&{{\rho _T}u}\\ {\Theta v}&0&\rho &0&{{\rho _T}v}\\ {\Theta w}&0&0&\rho &{{\rho _T}w}\\ {\Theta H - 1}&{\rho u}&{\rho v}&{\rho w}&{{\rho _T}H + \rho {C_p}} \end{array}} \right),\\ {\Gamma ^{ - 1}} = \left( {\begin{array}{*{20}{c}} {\frac{{\rho {C_p} + {\rho _T}\Psi }}{\Phi }}&{\frac{{{\rho _{\rm{T}}}u}}{\Phi }}&{\frac{{{\rho _T}v}}{\Phi }}&{\frac{{{\rho _T}w}}{\Phi }}&{ - \frac{{{\rho _T}}}{\Phi }}\\ { - u/\rho }&{1/\rho }&0&0&0\\ { - v/\rho }&0&{1/\rho }&0&0\\ { - w/\rho }&0&0&{1/\rho }&0\\ {\frac{{1 - \Theta \Psi }}{\Phi }}&{ - \frac{{\Theta u}}{\Phi }}&{ - \frac{{\Theta v}}{\Phi }}&{ - \frac{{\Theta w}}{\Phi }}&{\frac{\Theta }{\Phi }} \end{array}} \right), \end{array} $

其中,

$ \begin{array}{l} \Phi = \rho \Theta {C_p} + {\rho _T},\;\;\;\Psi = H - \left( {{u^2} + {v^2} + {w^2}} \right),\\ H = {C_p}T + \frac{1}{2}\left( {{u^2} + {v^2} + {w^2}} \right). \end{array} $

雅克比矩阵

$ \begin{array}{l} \frac{{\partial \hat H}}{{\partial \hat W}} = \left( {\begin{array}{*{20}{c}} {{\rho _p}U}&{\rho {n_x}}&{\rho {n_y}}&{\rho {n_z}}&{{\rho _T}U}\\ {{\rho _p}uU + {n_x}}&{\rho \left( {U + u{n_x}} \right)}&{\rho u{n_y}}&{\rho u{n_z}}&{{\rho _T}uU + {n_x}{\rho _T}}\\ {{\rho _p}vU + {n_y}}&{\rho v{n_x}}&{\rho \left( {U + v{n_y}} \right)}&{\rho v{n_z}}&{{\rho _T}vU + {n_z}{\rho _T}}\\ {{\rho _p}wU + {n_z}}&{\rho w{n_x}}&{\rho w{n_y}}&{\rho \left( {U + w{n_z}} \right)}&{{\rho _T}wU + {n_z}{\rho _T}}\\ {{\rho _p}HU}&{\rho \left( {H{n_x} + uU} \right)}&{\rho \left( {H{n_y} + vU} \right)}&{\rho \left( {H{n_z} + wU} \right)}&{{\rho _T}HU + \rho U{C_p}} \end{array}} \right),\\ {\Gamma ^{ - 1}}\frac{{\partial \hat H}}{{\partial \hat W}} = \left( {\begin{array}{*{20}{c}} {\frac{{\left( {{\rho _T} + \rho {C_p}{\rho _p}} \right)U}}{\Phi }}&{\frac{{{\rho ^2}{C_p}{n_x}}}{\Phi }}&{\frac{{{\rho ^2}{C_p}{n_x}}}{\Phi }}&{\frac{{{\rho ^2}{C_p}{n_x}}}{\Phi }}&0\\ {{n_x}/\rho }&U&0&0&0\\ {{n_y}/\rho }&0&U&0&0\\ {{n_z}/\rho }&0&0&U&0\\ {\frac{{\left( {{\rho _p} - \Theta } \right)U}}{\Phi }}&{\frac{{\rho {n_x}}}{\Phi }}&{\frac{{\rho {n_y}}}{\Phi }}&{\frac{{\rho {n_z}}}{\Phi }}&U \end{array}} \right), \end{array} $

对于量热完全气体可化简为

$ {\Gamma ^{ - 1}}\frac{{\partial \hat H}}{{\partial \hat W}} = \left( {\begin{array}{*{20}{c}} {M_r^2U}&{\rho U_r^2{n_x}}&{\rho U_r^2{n_y}}&{\rho U_r^2{n_z}}&0\\ {{n_x}/\rho }&U&0&0&0\\ {{n_y}/\rho }&0&U&0&0\\ {{n_z}/\rho }&0&0&U&0\\ {\frac{{\left( {M_r^2 - 1} \right)U}}{{\rho {C_p}}}}&{\frac{{U_r^2{n_x}}}{{{C_p}}}}&{\frac{{U_r^2{n_y}}}{{{C_p}}}}&{\frac{{U_r^2{n_z}}}{{{C_p}}}}&U \end{array}} \right). $

附录B 雅克比矩阵的特征系统

$ {\Gamma ^{ - 1}}\frac{{\partial \hat H}}{{\partial \hat W}} = \left( {\begin{array}{*{20}{c}} {M_r^2U}&{\rho U_r^2{n_x}}&{\rho U_r^2{n_y}}&{\rho U_r^2{n_x}}&0\\ {{n_x}/\rho }&U&0&0&0\\ {{n_y}/\rho }&0&U&0&0\\ {{n_z}/\rho }&0&0&U&0\\ {\frac{{\left( {M_r^2 - 1} \right)U}}{{\rho {C_p}}}}&{\frac{{U_r^2{n_x}}}{{{C_p}}}}&{\frac{{U_r^2{n_y}}}{{{C_p}}}}&{\frac{{U_r^2{n_z}}}{{{C_p}}}}&U \end{array}} \right). $

雅克比矩阵的特征值：λ_1,2,3=U,λ_4,5=U′ $\mp $C′.

其中

$ \begin{array}{l} U = {n_x}u + {n_y}v + {n_z}w,\\ U' = \frac{1}{2}U\left( {1 + M_r^2} \right),\\ C' = \frac{1}{2}\sqrt {{{\left( {1 - M_r^2} \right)}^2}{U^2} + {\rm{4}}M_r^2{C^2}} ,\\ C = c\sqrt {n_x^2 + n_y^2 + n_z^2} . \end{array} $

${{\Gamma }^{-1}}\frac{\partial \hat{H}}{\partial \hat{W}}$的特征矩阵

$ T = \left( {\begin{array}{*{20}{c}} 0&0&0&{\rho {C_p}}&{\rho {C_p}}\\ 0&{ - \frac{{{n_z}}}{{{n_x}}}}&{ - \frac{{{n_y}}}{{{n_x}}}}&{ - \frac{{2{n_y}{C_p}}}{r}}&{ - \frac{{2{n_y}{C_p}}}{s}}\\ 0&0&1&{ - \frac{{2{n_z}{C_p}}}{r}}&{ - \frac{{2{n_y}{C_p}}}{s}}\\ 0&1&0&{ - \frac{{2{n_z}{C_p}}}{r}}&{ - \frac{{2{n_z}{C_p}}}{s}}\\ 1&0&0&1&1 \end{array}} \right), $

$ {T^{ - 1}} = \left( {\begin{array}{*{20}{c}} { - \frac{1}{{\rho {C_p}}}}&0&0&0&1\\ 0&{ - \frac{{{n_x}{n_z}}}{{{n^2}}}}&{ - \frac{{{n_y}{n_z}}}{{{n^2}}}}&{\frac{{n_x^2 + n_y^2}}{{{n^2}}}}&0\\ 0&{ - \frac{{{n_x}{n_y}}}{{{n^2}}}}&{\frac{{n_x^2 + n_z^2}}{{{n^2}}}}&{ - \frac{{{n_y}{n_x}}}{{{n^2}}}}&0\\ {\frac{r}{{4\rho c'{C_p}}}}&{ - \frac{{{n_x}U_r^2}}{{2c'{C_p}}}}&{ - \frac{{{n_y}U_r^2}}{{2c'{C_p}}}}&{ - \frac{{{n_z}U_r^2}}{{2c'{C_p}}}}&0\\ { - \frac{s}{{4\rho c'{C_p}Q}}}&{\frac{{{n_x}U_r^2}}{{2c'{C_p}}}}&{\frac{{{n_y}U_r^2}}{{2c'{C_p}}}}&{\frac{{{n_z}U_r^2}}{{2c'{C_p}}}}&0 \end{array}} \right), $

其中,

$ \begin{array}{l} r = \left( {1 - M_r^2} \right)U + \sqrt {{{\left( {1 - M_r^2} \right)}^2}{U^2} + 4U_r^2{n^2}} ,\\ s = \left( {1 - M_r^2} \right)U - \sqrt {{{\left( {1 - M_r^2} \right)}^2}{U^2} + 4U_r^2{n^2}} ,\\ {n^2} = n_x^2 + x_y^2 + n_z^2. \end{array} $