0 引言

在流体力学数值模拟中，欧拉方法(Eulerian)和拉格朗日方法(Lagrangian,简称拉氏方法)是可压缩流体力学数值模拟的两类主要方法，国内外学者在这方面进行了大量的探索，取得了巨大的成就^[1]，这些方法在科学研究及实际应用中发挥了重要的作用.

欧拉方法对应流体力学方程的Euler形式，除了考虑由源项或拉格朗日项引起的变化，还必须考虑通过网格的物质输运，由于网格固定不动，给计算带来很大的方便，然而欧拉方法数值耗散大，模拟多介质流动时会遇到许多难以处理的问题.拉氏方法对应流体力学方程的Lagrange形式，在Lagrange形式中导数通常称物质时间导数，它包含了流体的输运项，与Euler形式都是用来描述同一物理过程，本质上是等价的，但在数值计算上两者却有很大的差异.由于不含输运项，拉氏方法计算公式简单，网格随流体运动，数值耗散小，界面清晰.自从Neumann和Richtmyer^[2]在一维计算中引入人工粘性处理激波取得成功后，人们自然希望将其推广到二维的计算中去，后经历了许多发展，取得了很大进展.然而当流场中存在剪切变形时，会导致Lagrange网格的扭曲变形，以至于很难在整个计算过程使用相同的Lagrange网格来处理.为了抑制网格的扭曲变形，在拉氏计算中加入网格重分以提高方法的抗变形能力，Hirt等所开创的ALE(Arbitrary Lagrangian-Eulerian)方法就是基于这一思想发展起来的^{[3, 4]}.一般来说ALE方法分为三步，即拉氏步、重分步和重映步，拉氏步由某时刻物理量出发，求解不含对流项的拉氏形式的方程，只考虑压力梯度对速度和能量改变的影响，并得到网格的拉氏位置和相应的物理量.重分步对网格进行重新构造得到较高质量的新网格，重映步则将拉氏网格上的物理量映射到新的网格上，这一方法由于比较灵活而得到较多的应用，在不改变网格拓扑结构时，对于真正的大变形问题存在与拉式方法同样的困难.

与ALE方法接近的是移动网格方法，Tang^{[5, 6]}等人发展了基于守恒插值的移动网格方法，与ALE不同，它第一步求解的是Euler方程，再进行网格的移动与重映.另一种移动网格方法由Harten等开创，它在时空多面体上运用有限体积方法，避免了显式的重映，后被发展到高维空间，但由于形式复杂，使得物理意义不明显，在高维时很难把握数值精度.介于Euler与Lagrange方法之间的另一种方法是所谓的统一坐标方法，借助统一坐标变换方法，Jin & Xu等^[7]发展了自适应变换的统一坐标变换的动理学数值方法，它仍然是利用坐标变换的思想，但这时不是对宏观的流体方程进行变换，而是对BGK方程进行坐标变换，得到逻辑空间的BGK方程，再构造相应的动理学数值方法，避免了复杂的逻辑空间的流体力学方程，比较容易处理粘性项，它充分保留了动理学方法的特点，对运动边界的流动问题的数值模拟具有很大的优越性，但需要构造充分大的计算区域，以避免边界的误差传递到内部区域.

在自适应变换的动理学数值方法的基础上，Ni等^{[8, 9, 10]}进一步发展了移动网格的动理学方法.它直接从积分形式的流体力学方程出发，对于任意的网格运动速度，得到严格意义上成立的离散格式，只要构造适当的网格移动速度，就可以进行物理量的更新，它避免了物理量的重映，这里的数值通量对通常的构造方法都适用，它是一种无重映的移动网格的数值方法.

与移动网格相似的还有自适应的网格划分AMR(Adaptive Mesh Refinement)技术，这一技术近年来也得到迅速发展，它根据物理量的变化对网格进行局部加密与粗化，网格的拓扑结构不断的发生变化，Berger^[11]在80年代初就进行了这方面的开创性的工作，先是对一般的双曲型方程研究了AMR方法，再用于气体动力学的数值求解中，之后这一方法用于物理、力学与工程等领域的数值模拟^{[12, 13]}，它的不足在于由于网格的结构的不断变化，计算程序的数据结构复杂，理论分析比较困难.

自适应的移动网格方法可以提高数值模拟精度与效率，其应用领域不断扩大，特别是运动边界问题的数值模拟^{[5, 14, 15, 16, 17, 18]}，它的特点是计算区域的边界运动是确定的，如振动Naca0012翼型问题，由于它在空气动力学中的重要性，已发展了一些不同的方法和技术，一般是在运动的网格上求解流体力学方程，为提高计算效率，通常是在计算区域生成非一致的三角网格，使得在机翼附近能有较高的分辨率，这样计算网格运动速度时比较简单，但是外边界需要特别进行处理，由于翼型的振动，计算区域要适当大，才能保证外边界的计算误差不影响翼型附近的流场，这给数值方法带来许多困难.

本文研究振动Naca0012翼型的无重映的移动网格数值模拟.该方法中，由于网格的运动速度是任意的，可以根据需要确定不同区域的网格速度，将计算区域的外边界固定，即外边界的网格速度为0，翼型附近的网格速度由翼型的振动速度确定，内部的网格速度则按照流场的分布自适应的调整，这样就可以直接进行单元上的物理量的更新.与以往的方法相比，是一种高效、高精度的数值方法.

1 移动非结构网格上的流体力学方程的离散格式

利用理想的可压流体力学方程模型，对于无粘的可压缩的流体力学方程，其微分形式有^[1]

$ \left\{ \begin{align} & \frac{\partial }{\partial t}\rho +\nabla \cdot \left( \rho U \right)=0, \\ & \frac{\partial }{\partial t}\left( \rho U \right)+\nabla \cdot \left( \rho UU+P \right)=0, \\ & \frac{\partial }{\partial t}\left( \rho E \right)+\nabla \cdot \left( \rho U\left( E+P \right) \right)=0, \\ \end{align} \right. $

(1)

其中的ρ,U,P,E分别为流体的密度、速度、压力及能量，对粘性流体力学，还需考虑应力及热传导等.若考虑控制体Ω(t)内流体的运动，设其边界速度为U_g，则对应的流体方程组的有积分形式

$ \left\{ \begin{align} & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho d\Omega }=-\int_{S\left( t \right)}{\rho \left( U-{{U}_{g}} \right)\cdot nds}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ud\Omega }=-\int_{S\left( t \right)}{\rho U\left( U-{{U}_{g}} \right)\cdot nds-\int_{S\left( t \right)}{pnds}}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ed\Omega }=-\int_{S\left( t \right)}{\rho E\left( U-{{U}_{g}} \right)\cdot nds}-\int_{S\left( t \right)}{pU\cdot nds}. \\ \end{align} \right. $

(2)

其中S(t)是控制体Ω(t)的边界,n是边界单位外法向.记e=E－U²/2为比内能. 当U_g=0，方程组(2)退化为流体力学方程欧拉形式(1)，当U_g=U时,则为对应的拉氏形式.

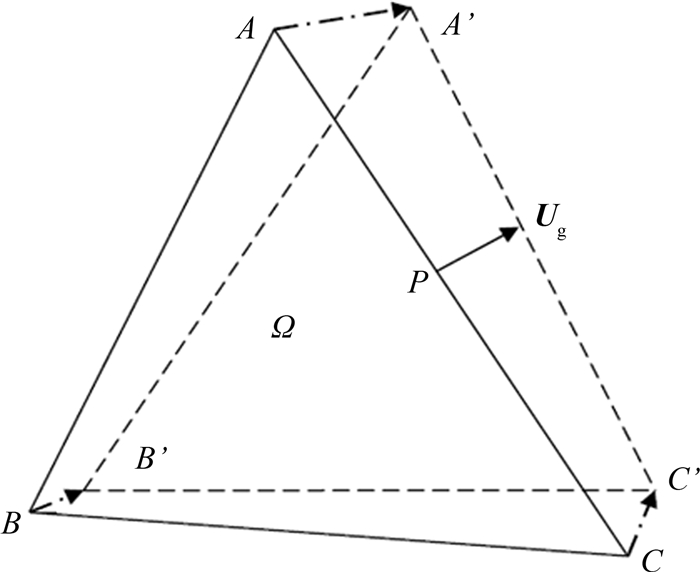
当Ω(t)取三角形单元,如图 1，定义单元边界的相对速度U=(U－U_g)，对应边e_i的速度记为Uⁱ=(U－U_g)|_ei. 方程组(2)可离散为

$ \left\{ \begin{align} & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho d\Omega }=\sum\limits_{i=1}^{3}{{{F}_{\rho ,{{e}_{i}}}}}\left( t \right), \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ud\Omega }=\sum\limits_{i=1}^{3}{\left( {{F}_{\rho {{U}_{{{e}_{i}}}}}}\left( t \right)+U_{g}^{i}{{F}_{\rho ,{{e}_{i}}}}\left( t \right) \right)}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ed\Omega }=\sum\limits_{i=1}^{3}{\left( {{F}_{\rho E,{{e}_{i}}}}\left( t \right)+U_{g}^{i}{{F}_{\rho {{U}_{{{e}_{i}}}}}}\left( t \right)+\frac{1}{2}{{\left( U_{g}^{i} \right)}^{2}}{{F}_{\rho ,{{e}_{i}}}}\left( t \right) \right)}, \\ \end{align} \right. $

(3)

其中

$ \left\{ \begin{align} & {{F}_{\rho ,{{e}_{i}}}}\left( t \right)=-\int_{{{e}_{i}}}{\rho U\cdot nds}, \\ & {{F}_{\rho U{{e}_{i}}}}\left( t \right)=-\int_{{{e}_{i}}}{\rho UU\cdot nds}+\int_{{{e}_{i}}}{pnds,} \\ & {{F}_{\rho E,{{e}_{i}}}}\left( t \right)=-\int_{{{e}_{i}}}{\rho \left( \frac{1}{2}{{U}^{2}}+\varepsilon \right)U\cdot nds}+\int_{{{e}_{i}}}{pnds}, \\ \end{align} \right. $

这里F_ρ,ei,F_ρUei,F_ρE,ei分别为通过边界e_i的质量通量、动量通量和能量通量.(3)式表明只需运动边界上的流通量，则可以更新单元上的物理量.

为构造边界上的数值通量，将边界运动速度分解为法向与切向速度分量,记边界e_i法向方向为n=(cosα,sinα)，速度为U=(U,V)，则法向速度U′和切向速度V′分量为

$ \left\{ \begin{align} & U'=U\cos \alpha +V\sin \alpha ,\\ & V'=-U\sin \alpha +V\cos \alpha . \\ \end{align} \right. $

这样可将方程组 (3) 离散为

$ \left\{ \begin{align} & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho d\Omega }=\sum\limits_{i=1}^{3}{{{F}_{\rho ,{{e}_{i}}}}\left( t \right)}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ud\Omega }=\sum\limits_{i=1}^{3}{{{F}_{\rho Y,{{e}_{i}}}}\left( t \right)}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Vd\Omega }=\sum\limits_{i=1}^{3}{{{F}_{\rho V,{{e}_{i}}}}\left( t \right)}, \\ & \frac{d}{dt}\int_{\Omega \left( t \right)}{\rho Ed\Omega }=\sum\limits_{i=1}^{3}{{{F}_{\rho E,{{e}_{i}}}}\left( t \right)}, \\ \end{align} \right. $

(4)

其中

$ \left\{ \begin{align} & {{F}_{\rho U,{{e}_{i}}}}\left( t \right)=\sin \alpha {{F}_{\rho U',{{e}_{i}}}}\left( t \right)+\cos \alpha {{F}_{\rho V',{{e}_{i}}}}\left( t \right)+U_{g}^{i}{{F}_{\rho ,{{e}_{i}}}}\left( t \right), \\ & {{F}_{\rho V,{{e}_{i}}}}\left( t \right)=-\cos \alpha {{F}_{\rho U',{{e}_{i}}}}\left( t \right)+\sin \alpha {{F}_{\rho V',{{e}_{i}}}}+V_{g}^{i}{{F}_{\rho ,{{e}_{i}}}}\left( t \right), \\ & {{F}_{\rho E,{{e}_{i}}}}\left( t \right)={{F}_{\rho E,{{e}_{i}}}}\left( t \right)+\left( U_{g}^{i}\sin \alpha -V_{g}^{i}\cos \alpha \right){{F}_{\rho U',{{e}_{i}}}}\left( t \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( U_{g}^{i}\cos \alpha +V_{g}^{i}\sin \alpha \right){{F}_{\rho V',{{e}_{i}}}}\left( t \right)+\frac{1}{2}\left[ {{\left( U_{g}^{i} \right)}^{2}}+{{\left( V_{g}^{i} \right)}^{2}} \right]{{F}_{\rho ,{{e}_{i}}}}\left( t \right). \\ \end{align} \right. $

方程组(4)是移动网格下有限体积半离散格式. 记不同时刻的控制体Ω′=Ω(tⁿ⁺¹)和Ω=Ω(tⁿ)，控制体上质量、动量和能量的质量平均值定义为

$ \bar{\rho }\left( t \right)=\frac{1}{\Omega }\int_{\Omega }{\rho \left( x,t \right)dx},\bar{\rho }\bar{U}\left( t \right)=\frac{1}{\Omega }\int_{\Omega }{\rho U\left( x,t \right)dx},\bar{\rho }\bar{E}\left( t \right)=\frac{1}{\Omega }\int_{\Omega }{\rho E\left( x,t \right)dx}. $

对半离散格式(4)，从时间tⁿ到tⁿ⁺¹积分,由此得到方程组(4)的全离散格式，其分量形式，

$ \left\{ \begin{align} & {{{\bar{\rho }}}^{n+1}}=\left( {{{\bar{\rho }}}^{n}}\left| \Omega \right|+\sum\limits_{i=1}^{3}{{{\Gamma }_{\rho ,{{e}_{i}}}}} \right)/\left| \Omega ' \right|, \\ & \bar{\rho }{{{\bar{U}}}^{n+1}}=\left( \bar{\rho }{{{\bar{U}}}^{n}}\left| \Omega \right|+\sum\limits_{i=1}^{3}{{{\Gamma }_{\rho U,{{e}_{i}}}}} \right)/\left| \Omega ' \right|, \\ & \bar{\rho }{{{\bar{V}}}^{n+1}}=\left( \bar{\rho }{{{\bar{V}}}^{n}}\left| \Omega \right|+\sum\limits_{i=1}^{3}{{{\Gamma }_{\rho V,{{e}_{i}}}}} \right)/\left| \Omega ' \right|, \\ & \bar{\rho }{{{\bar{E}}}^{n+1}}=\left( \bar{\rho }{{{\bar{E}}}^{n}}\left| \Omega \right|+\sum\limits_{i=1}^{3}{{{\Gamma }_{\rho E,{{e}_{i}}}}} \right)/\left| \Omega ' \right|. \\ \end{align} \right. $

(5)

其中Γ_Φ,ei=ΔtF_Ψ,ei(t).

式(5)中的数值通量可以利用不同的方法得到，这里利用Riemann解法器构造,由于本文考虑的是理想流体，在一维方程组的情形，通过解Riemann问题得到相应的解析解，再根据波速的值通过取样到中心点的值，进而得到相应的数值通量，对二维方程组的情形，则采用分裂方法得到，这里不再叙述，具体步骤可参考文献[19].

2 网格移动速度

对振动Naca0012翼型的数值模拟，这里根据计算区域的特点，考虑三种类型的网格速度，计算区域外边界、内边界及计算区域内部三种，计算区域外边界固定，所以，速度为零，计算区域内边界由翼型的周期运动确定，而计算区域的内部则利用自适应的移动方法确定，若能确定下一时刻的网格节点位置，则就得到当前时刻到下一时刻的平均速度，即

$ {{U}_{g}}=\left( {{X}^{n+1}}-{{X}^{n}} \right)/\Delta t, $

其中Xⁿ⁺¹和Xⁿ分别为新旧网格节点坐标,Δt是时间步长,再利用线性关系就得到边界的移动速度.

新时刻位置利用变分原理得到,它基于等分布原理，假设x=x(ξ)是计算域到物理域的坐标映射,ξ=ξ(x)是逆映射. 定义计算区域网格能量泛函为

$ E\left( x \right)=\frac{1}{2}\sum\limits_{k=1}^{d}{\int_{\Omega k}{{{\nabla }^{T}}{{x}_{k}}{{G}_{k}}\nabla {{x}_{k}}d\xi }}, $

(6)

其中d是空间维数,G_k是给定的对称正定矩阵,形式为G_k=wI，其中I是单位矩阵,w是非负加权函数. 利用其极小化原理就可以得到相应的微分方程，能量泛函 (6) 对应的欧拉-拉格朗日方程为

$ \nabla \cdot \left( w\nabla {{x}_{k}} \right)=0,\ \ \ 1\le k\le d. $

(7)

利用有限体积方法可得到网格移动方程 (7) 的离散格式即离散的网格方程,加权函数w取值为

$ w=\sqrt{1+{{\alpha }_{1}}{{\left( \frac{{{u}_{\xi }}}{\underset{\xi }{\mathop{\max }}\,\left| {{u}_{\xi }} \right|} \right)}^{2}}+{{\alpha }_{2}}{{\left( \frac{{{s}_{\xi }}}{\underset{\xi }{\mathop{\max }}\,\left| {{s}_{\xi }} \right|} \right)}^{2}}}. $

其中熵s=p/ρ^γ，u_ξ为相应单元的物理量,α₁和α₂是可调非负参数,数值算例中取值为1.0与10.0,它由数值实验确定.

3 振动Naca0012翼型的数值模拟

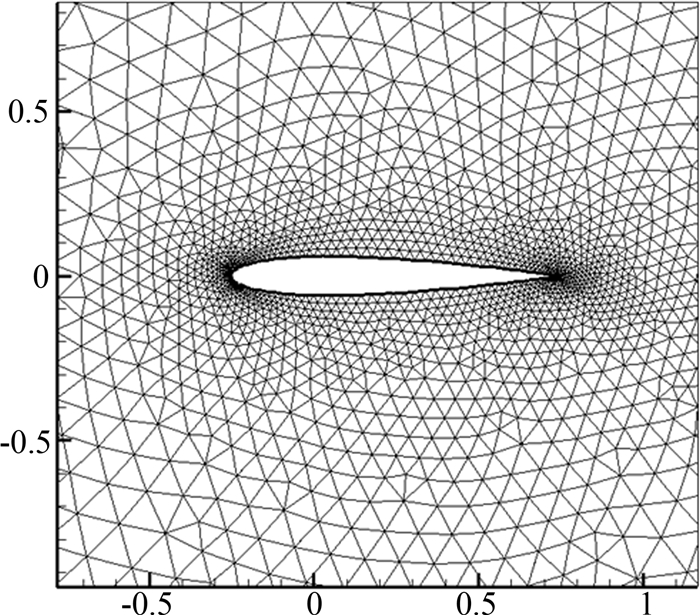
本节利用上述移动网格方法振动Naca0012翼型进行直接的数值模拟,翼型是标准的三维机翼的截面，翼弦为通过翼型的前缘与后缘的连线，取单位长1，翼型的中心为弦线上距前缘1/4的点，翼型的振动则围绕中心点上下运动.图 2是在翼型附近生成的局部的非结构网格.

该问题是空气动力学的重要研究对象，目前对该问题的数值模拟分两类，一种是固定翼型的模拟，在数值模拟中，考虑一致的流场穿过翼型，经过一个时间段，翼型附近的流场可以达到稳定的状态.另一种是翼型作周期性的振动，在数值模拟中，翼型附近的网格与翼型作为整体运动，在通常的数值方法中，处理此类问题有一定的难度.本文中的移动网格方法比较容易处理，由于网格的运动速度是任意的，这里将计算区域的边界固定，翼型附近的网格与翼型的振动一致，其余的网格则按照流场的分布自动调整，即为上节中给定的移动网格方法，剩下只需给定初始条件.

初始条件参考文[7]中算例给出，这里考虑计算区域[－10,10]×[－10,10]，区域的非结构网格单元数为7 366，翼弦绕翼型的中心点的角度运动方程为α=α_m+α₀ sin (ωt)，其中α为翼弦与x轴的夹角,ω为振动频率，这里取α_m=0.016°，α₀=-2.51°.

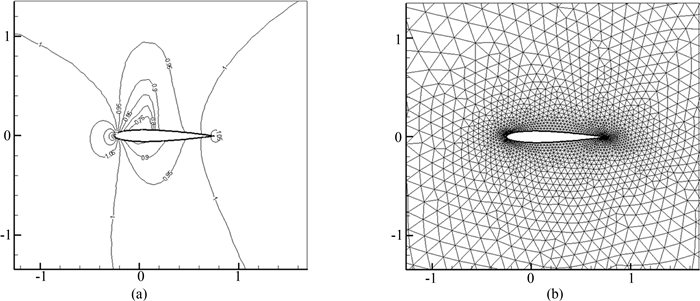
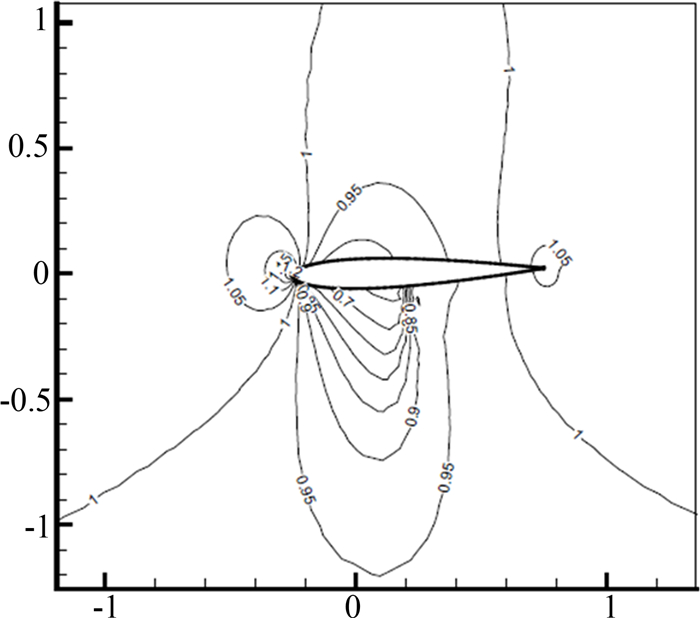
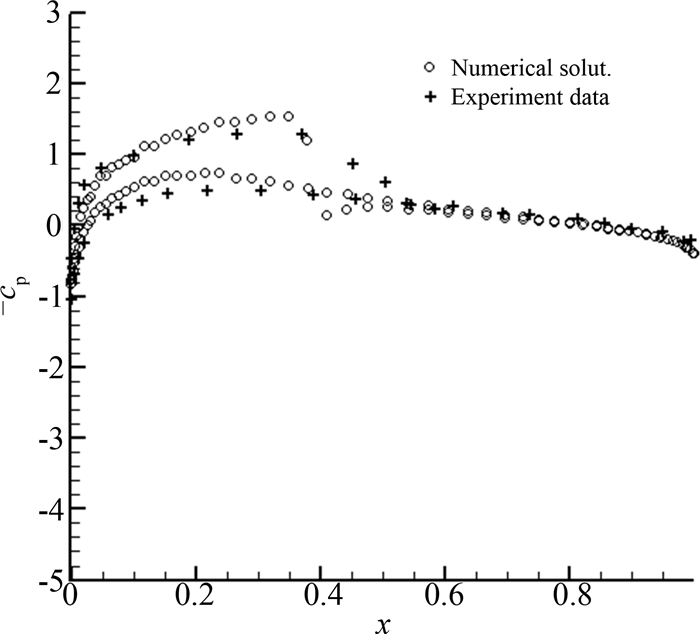
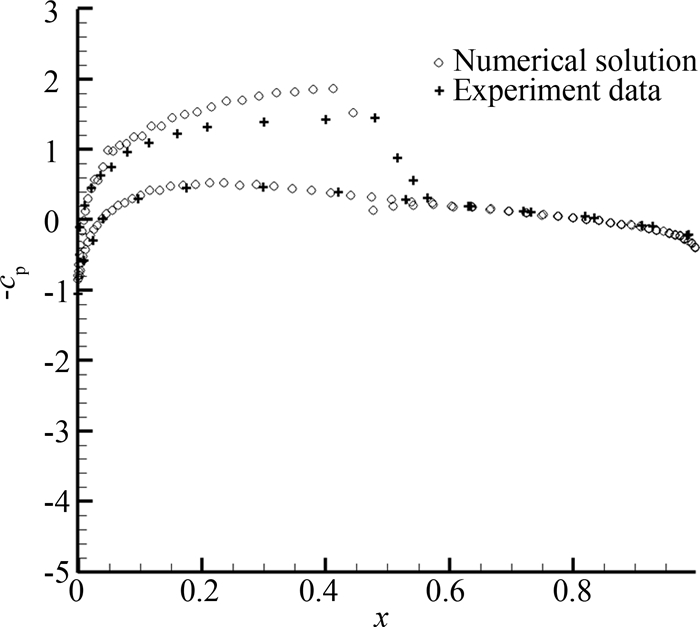
流体的初始密度与速度均为1，来流马赫数为0.755，计算区域左侧为入流边界条件，右侧为出流边界条件，上下均为一致流条件.数值结果如图 3~图 6所示,图 3和图 4分别对应α=－2.0°与α=2.01°时的密度等值线及网格分布，图 5和图 6则为相应的压强系数(c_p)分布，并给出与实验的对比，实验数据取自文献[7]，压强系数的计算公式为

$ {{c}_{p}}=\left( p-{{p}_{\infty }} \right)/\left( \rho u_{\infty }^{2}/2 \right), $

u_∞,p_∞为来流速度与压力，压强系数与文[7]中利用统一坐标变换的动理学格式结果吻合.

4 结论

给出振动Naca0012翼型问题的移动网格数值模拟. 这种移动网格方法避免了传统的移动网格方法中新旧网格物理量之间的重映,利用振动机翼Naca0012的特殊性，将网格的移动分成三类，对计算区域的内部网格，利用自适应移动网格方法得到网格移动速度,并在移动网格上计算流通量,实现物理量更新，它将一个运动边界问题的数值模拟转化为固定区域上的数值模拟，避免了繁琐的技术处理，提高了计算效率.数值试验表明,使用此格式获得了令人满意的数值结果.