| 基于GPU集群的Level Set并行高精度演化 |
数值模拟,特别是基于粒子的数值模拟所产生的数据场经常含有噪声.无网格数据转换成均匀网格时会产生噪声. EM(Electron Microscope,电子显微镜),MRI(Magnetic Resonance Imaging,磁共振成像)和CT(Computed Tomography,电子计算机断层扫描)等测量结果中难免带有噪声.由于噪声的存在,使人分辨不清物质界面和特征,给数据分析带来了困难,因此,需要对数据进行去噪处理.另一方面,在高性能计算机系统上,数值模拟产生大规模数据;随着测量仪器分辨率的提高,科学实验中也产生大规模数据.单个处理机已经很难对如此大规模的数据进行处理和绘制.大规模数据场需要高效的并行处理技术.
高档GPU是众核(many-core)处理器,它具有很强的并行计算能力.例如,Nvidia Quadro FX 5600图形卡,显存1.5GB,拥有128核. CUDA[1]是通用并行计算平台和应用程序编程接口,利用CUDA可以很方便地在GPU上实现通用计算.借助大规模GPU集群,能够大大提高数据场演化速度.GPU集群是混合体系结构.基于GPU集群的并行计算的基本思路是,将计算任务分配给各个计算节点,各计算节点由进程并行执行计算任务,每个进程内部在GPU上采用多线程进行并行计算.GPU集群的并行计算主要可以分为两个层次,进程级并行和线程级并行,是混合并行[2].
在Osher和Sethian提出的Level Set方法[3],Level Set(水平集、等值面)的演化速度是曲率的函数.数据场演化方程不同的演化模型,形式有所不同.Level Set方法可以用于去除噪声.用Level Set方法去除噪声,演化方程作用于整个数据场,而不仅仅作用于0值Level Set的邻域.Rosenfeld等给出多尺度特征(边界和曲线)探测结果[4].Witkin采用Gauss滤波实现1维多尺度滤波[5].它给出规范的公式,这个公式容易推广到高维[5].这里核函数为高斯函数.事实上,它是热扩散方程的解[5].从物理上讲,在热扩散的过程中,温度的分布越来越平滑,因此热扩散方程可以光顺图像.Perona和 Malik给出图像滤波方法[6] (简称为P&M方法),如果g′为常数,得到各向同性的热传导方程[5].解该方程等价于对能量泛函求极小值.热传导方程就是能量泛函 $ \int_{U}{{{\left\| \nabla I \right\|}^{2}}dxdy}$求极小值.通过对图像的各向异性扩散,光顺数据(去除噪声)并保持特征(edge).Alvarez 等人给出 $\partial \phi /\partial t=\left\| \nabla \phi \right\|g\left( \left\| \nabla \phi \right\| \right)\left( \nabla \cdot \left( \nabla \phi /\left\| \nabla \phi \right\| \right) \right)$[7],用于图像光顺和特征探测. Caselles等给出测地模型,它是黎曼空间面积∫Sg(‖▽I‖2)da(或长度)极小模型[8].如果g为常数,就是欧几里德空间的 $\int_{S}{da}$面积(或长度)极小模型.测地模型主要用于数据场分割.Rudin等给出Level Set演化的约束变分模型,能量泛函为 $E=\int\limits_{\Omega }{\sqrt{u_{x}^{2}+u_{y}^{2}}dxdy} $,约束条件为 $ \int\limits_{\Omega }{udxdy}=\int\limits_{\Omega }{{{u}_{0}}dxdy},\int\limits_{\Omega }{{{\left( u-{{u}_{0}} \right)}^{2}}}dxdy={{\sigma }^{2}}$图像中噪声的平均值为0,标准差为σ[9].该方法可以看作P&M方法的特例,$ g\left( \xi \right)=2\sqrt{\xi }$.
传统方法采用迎风格式近似地表示导数,从而得到差分方程,然后进行演化计算,这会带来一定的误差. B样条基函数的极限是高斯函数,B样条基函数导数的极限是高斯函数的导数[11, 12],而高斯函数是热扩散方程解的核函数[6]. 在演化计算中引入张量积B样条函数是自然的选择.
我们用Level Set方法去除3D数据场中的噪声.在GPU上实现基于B样条和均匀网格的Level Set方程解法器.在基于B样条函数的演化过程中每个时间步都需要反算B样条系数.反算B样条系数需要迭代方法或直接解法.由于GPU计算需要首先将数据从CPU内存装入GPU内存.虽然高档GPU和CPU之间可以采用PCI Express总线进行高速数据传输,数据从CPU内存传输到GPU内存需要一定的时间开销.在并行演化计算中如果采用迭代算法,需要不断从GPU中取出边界数据,在计算节点之间交换边界数据,并更新GPU内存中的相应数据,交换次数相对较多,这样会降低性能.如果分布于计算节点上的数据较大,在一步迭代中需要多次在CPU和GPU之间交换数据,真正的迭代计算时间很短,而数据交换时间较长,这样会大大降低性能.需要寻求非迭代的适合于GPU的反算B样条系数的方法.
1 算法 1.1 基于B样条的Level Set基本演化算法Level Set又可以称为等值面,一般方程为Φ(x,y,z,t)=C.方程两边对时间求导,得到等值面的演化方程∂Φ/∂t+▽Φ·v=0,又可以写成∂Φ/∂t+((▽Φ/‖▽Φ‖)·v)‖▽Φ‖=0,令vN=(▽Φ/‖▽Φ‖)·v,方程变成∂Φ/∂t+vN‖▽Φ‖=0,令vN=-F,方程可以写成
| $ \frac{\partial \phi }{\partial t}=F\left\| \nabla \phi \right\|, $ | (1) |
F一般为曲率的函数,三维空间点A(x0,y0,z0)的曲率是指过A点的等值面(Φ(x,y,z)=C)在点A的曲率.本文研究三维数据场的演化,F取为平均曲率κM,该模型称为平均曲率模型,它为面积极小模型.该模型可以起到光顺作用.
| $ {{\kappa }_{M}}\left\| \nabla \phi \right\|=\frac{{{\phi }_{xx}}\left( \phi _{y}^{2}+\phi _{z}^{2} \right)+{{\phi }_{yy}}\left( \phi _{x}^{2}+\phi _{z}^{2} \right)+{{\phi }_{zz}}\left( \phi _{x}^{2}+\phi _{y}^{2} \right)-2{{\phi }_{xy}}{{\phi }_{x}}{{\phi }_{y}}-2{{\phi }_{yz}}{{\phi }_{y}}{{\phi }_{z}}-2{{\phi }_{xz}}{{\phi }_{x}}{{\phi }_{z}}}{\phi _{x}^{2}+\phi _{y}^{2}+\phi _{z}^{2}} $ |
定义算子Η:$H\left( \phi \right)=\frac{{{\phi }_{xx}}\left( \phi _{y}^{2}+\phi _{z}^{2} \right)+{{\phi }_{yy}}\left( \phi _{x}^{2}+\phi _{z}^{2} \right)+{{\phi }_{zz}}\left( \phi _{x}^{2}+\phi _{y}^{2} \right)-2{{\phi }_{xy}}{{\phi }_{x}}{{\phi }_{y}}-2{{\phi }_{yz}}{{\phi }_{y}}{{\phi }_{z}}-2{{\phi }_{xz}}{{\phi }_{x}}{{\phi }_{z}}}{\phi _{x}^{2}+\phi _{y}^{2}+\phi _{z}^{2}}$时间均匀离散,时间步用p表示,时间步长用Δt表示,得到方程
| $ {{\phi }^{p+1}}={{\phi }^{p}}+H\left( {{\phi }^{p}} \right)\Delta t, $ | (2) |
3D空间离散成直线网格,网格结点用(i,j,k)表示;约定任意标量函数f在网格结点(i,j,k)上的值用fi,j,k表示. 据此,得到方程
| $ \phi _{i,j,k}^{p+1}=\phi _{i,j,k}^{p}+{{H}_{i,j,k}}\Delta t, $ | (3) |
其中,Hi,j,k=(H(Φp))i,j,k,i=d,…,L+1; j=d,…,M+1; k=d,…,N+1; p=0,1,….
在演化过程中,我们采用B样条[12, 13, 14],提高演化精度.在三维情况下,分别用Ni,dx(x),i=0,L; Nj,dy(y),j=0,M; Nk,dz(z),k=0,N表示定义于结点向量(x0,x1,…,xL+d+1),(y0,y1,…,yM+d+1),(z0,z1,…,zN+d+1)上的d(d≥3)次B样条基函数.在演化过程中,对每个时间步p(这里是人工时间),令
| $ {{\phi }^{p}}\left( x,y,z \right)=\sum\limits_{k=0}^{N}{\sum\limits_{j=0}^{M}{\sum\limits_{i=0}^{L}{c_{i,j,k}^{p}}N_{j,d}^{y}\left( y \right)N_{k,d}^{z}\left( z \right)}},\left( x,y,z \right)\in \left[{{x}_{d}},{{x}_{L+1}} \right]\times \left[{{y}_{d}},{{y}_{M+1}} \right]\times \left[{{z}_{d}},{{z}_{N+1}} \right], $ |
系数cj,k,lp是B样条系数.Φp是定义于3D直线网格上的张量积B样条函数,它在网格结点(i,j,k)上的值等于Φi,j,kp,i=d,…,L+1; j=d,…,M+1; k=d,…,N+1; 即Φp插值于Φi,j,kp. Φp的一阶偏导数、二阶偏导数或更高阶导数、曲率可以精确计算.
在本文中,p时刻演化函数Φp用定义于均匀网格上的三三次均匀B样条函数表示,要计算Hi,j,k,必须根据Φpi,j,k,反算出B样条系数ci,j,ki,即在每步演化前必须进行插值计算.反算B样条系数ci,j,kp,分三步进行,每一步沿一个方向反算.考虑到B样条基函数的局部支撑性,在沿某个方向进行计算时,沿该方向B样条系数具有局部相关性,B样条系数之间的关系可以用三对角方程组表示;在其它方向上数据没有相关性.
在实际计算中,以原始数据作为初值.在反算B样条系数时,令边界外结点的系数等于边界结点的系数.
在用追赶法解三对角方程组时,先进行LU分解,然后计算消元和回代过程.由于演化方程的解用张量积形式表示.沿同一方向,所有扫描行的三对角方程组的系数矩阵完全相同.在演化过程中,这些系数也不变化.因此,在整个演化过程中,每个方向只需要计算一次LU分解.
在演化过程中,采用三次B样条插值,Φ可以达到四阶精度,Φx,Φy,Φz,Φxy,Φyz,Φxz可以达到三阶精度,Φxx,Φyy,Φzz可以达到二阶精度,因此采用B样条进行演化可以期望达到较高的精度.采用一阶迎风格式的演化算法,只能达到一阶精度.
1.2 基于GPU集群的混合并行演化算法用笛卡尔网格组织当前的计算节点组,并按照同样的笛卡尔网格划分数据空间,即将全局空间(定义域)划分成Lp×Mp×Np的块(如图 1(a)),每一块分配到一个计算节点.沿每个方向,基于网格结点进行划分,分开的两部分不共享网格结点.
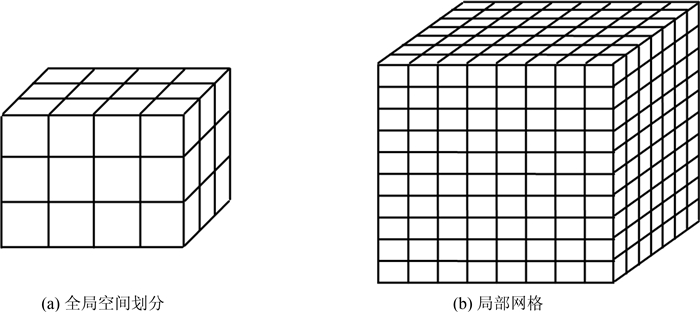 |
| 图1 全局空间划分与局部网格 Fig. 1 Whole space partition and local grid |
在每个计算节点中,如图 1(b),局部网格G(L×M×N)沿z方向的投影网格为Gz(尺寸为L×M),Gz每个网格结点对应G中z方向一行网格结点,称为z向局部扫描行,共有L×M扫描行.类似地,可以定义y向局部扫描行和x向局部扫描行.全局网格沿某个方向的一行网格结点,称为该方向的全局扫描行.全局扫描行与局部网格相交的部分就是相应方向的局部扫描行.
由于p时刻演化函数Φp用三三次B样条函数(张量积形式)表示,在数据场演化过程中,每个演化步,由两个阶段组成:
phase 1 反算B样条系数;
phase 2 根据式(3)进行演化计算.
现在分析每个演化步的并行性:
1) 由于三维张量积B样条系数的反算可以分解成三个1维 B样条系数的反算. 在沿某个方向进行计算时,沿该方向B样条系数具有相关性,B样条系数之间的关系可以用三对角方程组表示;在其它方向上B样条系数没有相关性.在沿某个方向反算B样条系数时,计算节点之间沿该方向存在相互依赖关系,在其它方向没有相互依赖关系. 这样把三维相关性转化为一维相关性,提高了并行度.
2) 计算每个网格结点的函数值,一阶导数、二阶导数值,需要取出以该网格结点为中心的2×2×2邻域网格(结点数为3×3×3)结点上的B样条系数.每个计算节点的局部网格中应该沿每个方向在边界上增加1层虚网格,每个方向的扫描行数也相应增加.虚网格结点上的B样条系数在phase 1通过通信或计算得到.大量的计算集中在phase 2,phase 2并行性很好.
反算B样条系数就是解三对角方程组,可以采用迭代方法或直接方法.如果采用迭代方法反算B样条系数,需要不断在计算节点之间交换边界数据,并更新GPU内存中的相应数据,交换次数相对较多,这样会降低性能.因此本文采用直接方法解三对角方程组.
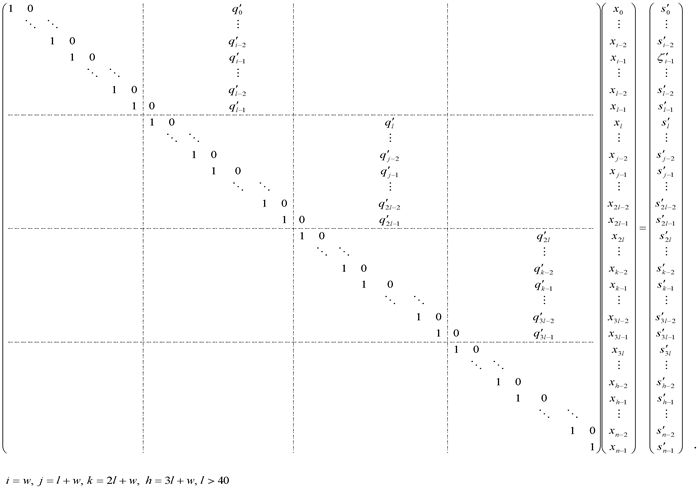
这里先给出解一个方程组的并行算法原理.对三对角系数矩阵A进行LU分解,于是A=LU.方程组Ax=r化成两个方程组Lζ=r,Ux=ζ.其中
| $ \begin{align} & A=\left( \begin{matrix} {{a}_{0}} & {{c}_{0}} & {} & {} & {} & {} & {} \\ {{b}_{1}} & {{a}_{1}} & {{c}_{1}} & {} & {} & {} & {} \\ {} & \ddots & \ddots & \ddots & {} & {} & {} \\ {} & {} & {{b}_{i}} & {{a}_{i}} & {{c}_{i}} & {} & {} \\ {} & {} & {} & \ddots & \ddots & \ddots & {} \\ {} & {} & {} & {} & \ddots & \ddots & {{c}_{n-2}} \\ {} & {} & {} & {} & {} & {{b}_{n-1}} & {{a}_{n-1}} \\ \end{matrix} \right),\\ & L=\left( \begin{matrix} {{\alpha }_{0}} & {} & {} & {} & {} & {} & {} \\ {{b}_{1}} & {{\alpha }_{1}} & {} & {} & {} & {} & {} \\ {} & \ddots & \ddots & {} & {} & {} & {} \\ {} & {} & {{b}_{i-1}} & {{\alpha }_{i-1}} & {} & {} & {} \\ {} & {} & {} & {{b}_{i}} & {{\alpha }_{i}} & {} & {} \\ {} & {} & {} & {} & \ddots & \ddots & {} \\ {} & {} & {} & {} & {} & {{b}_{n-1}} & {{\alpha }_{n-1}} \\ \end{matrix} \right),\\ & U=\left( \begin{matrix} 1 & {{\gamma }_{0}} & {} & {} & {} & {} & {} \\ {} & \ddots & \ddots & {} & {} & {} & {} \\ {} & {} & 1 & {{\gamma }_{i-1}} & {} & {} & {} \\ {} & {} & {} & 1 & {{\gamma }_{i}} & {} & {} \\ {} & {} & {} & {} & \ddots & \ddots & {} \\ {} & {} & {} & {} & {} & 1 & {{\gamma }_{n-2}} \\ {} & {} & {} & {} & {} & {} & 1 \\ \end{matrix} \right). \\ \end{align} $ |
解Lζ=r的过程也称为“追”的过程,解Ux=ζ的过程也称为“赶”的过程.在基于张量积B样条的演化过程中,每个方向存在许多方程组,并且方程组的系数相同,每个计算节点预先在CPU上采用双精度精确计算整体的LU分解,这只要很少的时间.
Larriba-Pey等针对向量机研究了对角占优的二对角方程组的R-CR和OPM方法[15]. 在R-CR方法中需要计算Spike,在OPM方法中方程组的划分有交叠部分.在本文中,采用均匀B样条,a0=5/6,c0=1/6,对f(n-1>f>0),af=4/6,bf=cf=1/6; an-1=5/6,bn-1=1/6.其中,α0=a0,α0γ0=c0,对f(n>f>0),αf+γf-1bf=af,αfγf=cf;不难证明αi>(2+3)/6,而且当i<n-1并且i较大时,αi≈(2+3)/6.首先分析方程组Lζ=r的解,消去系数矩阵第1行到n-1行的次对角元,并适当调整右端向量:r01=r0,对n>f>0,rf1=rf-(bf/αf-1)rf-11.对n>f≥0,ζf=rf1/αf.于是对n>f>w+1,有rf1=rf+ $\sum\limits_{i=1}^{w}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{b}_{f-j}}}/{{\alpha }_{f-j-1}} \right){{r}_{f-i}}+{{\left( -1 \right)}^{w+1}}pr_{f-w-1}^{1}$,$p={{\left( -1 \right)}^{w+1}}\left( \prod\limits_{j=0}^{w}{{{b}_{f-j}}/{{\alpha }_{f-j-1}}} \right) $,$ r_{f-w-1}^{1}={{r}_{f-w-1}}+\sum\limits_{i=1}^{f-w-1}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{b}_{f-w-1}}}/{{\alpha }_{f-w-i-1}} \right){{r}_{f-w-i-1}}r_{f-w-1}^{1}$是rg(0≤g<f-w)的线性组合.在本文中,$\left| p \right|=\prod\limits_{j=0}^{w}{\left| {{b}_{f-j}} \right|}/\left| {{\alpha }_{f-j-1}} \right|<{{\left( 1/\left( 2+\sqrt{3} \right) \right)}^{w+1}}\left( {{\log }_{10}}\left( 2+\sqrt{3} \right)<0.5719 \right)$,如果w足够大,p是一个很小的数,rg(0≤g<f-w)对ζf的影响很小. 如果w=20,当n>f>21,|p|<10-12.于是,可以忽略(-1)w+1pr1f-w-1,得到近似解 $\zeta {{'}_{f}}=\left[{{r}_{f}}+\sum\limits_{i=1}^{w}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{b}_{f-i}}/{{\alpha }_{f-j-1}}} \right){{r}_{f-i}} \right]/{{\alpha }_{f}}$,在此基础上可以依次解出后面的近似解. 方程组中第f-w到第f-1行方程称为后面方程的关联方程组,这里w称为关联方程组的宽度. ζ′f只依赖于关联方程组.
现在分析方程组Ux=ζ的解,从下到上依次消去第n-2行到第0行的上次对角元并适当调整右端向量ζ的相应元素: sn-1=ζn-1,对n-1>f≥0,sf=ζf-γfsf+1.对n>f≥0,xf=sf.对n-w-2>f≥0,${{s}_{f}}={{\zeta }_{f}}+\sum\limits_{i=1}^{w}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{\gamma }_{f+j}}} \right){{\zeta }_{f+j}}+{{\left( -1 \right)}^{w+1}}q{{s}_{f+w+1}}$,$q={{\left( -1 \right)}^{w+1}}\prod\limits_{j=0}^{w}{{{\gamma }_{f+j}}}$,${{s}_{f+w+1}}={{\zeta }_{f+w+1}}+\sum\limits_{i=1}^{n-f-w-2}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{\gamma }_{f+w+j+1}}} \right){{\zeta }_{f+w+i+1}}$.如果w足够大,q是一个很小的数,ζg(n-1>g>f+w)对xf影响很小. 如果w=20,当n-22>f>0,相应的|q|<10-12,忽略(-1)w+1qsf+w+1,可以得到近似解 $x{{'}_{f}}={{\zeta }_{f}}+\sum\limits_{i=1}^{w}{{{\left( -1 \right)}^{i}}}\left( \prod\limits_{j=0}^{i-1}{{{\gamma }_{f+j}}} \right){{\zeta }_{f+i}}$,在此基础上,可以依次解出前面的解. 方程组中第f+1到第f+w称为前面方程的关联方程组. x′f的计算依赖于宽度为w的关联方程组.
三次样条插值基函数是波动函数,其振幅是指数衰减的[16],由此也可以说明远处的插值基点上的值,对B样条系数的影响较小.这与上面的分析是一致的.
基于以上分析给出如下的解三对角方程组的并行算法原理.
设某一方向的计算节点数为np,用np个计算节点解三对角方程组Ax=r.为便于描述,设系数矩阵A的阶数为n=npl,l≥40.将方程组尽可能均匀地划分成np个子方程组,并分配给np个计算节点. 下面以np=4为例说明三对角方程组的并行解法.设当前计算节点号为ip.
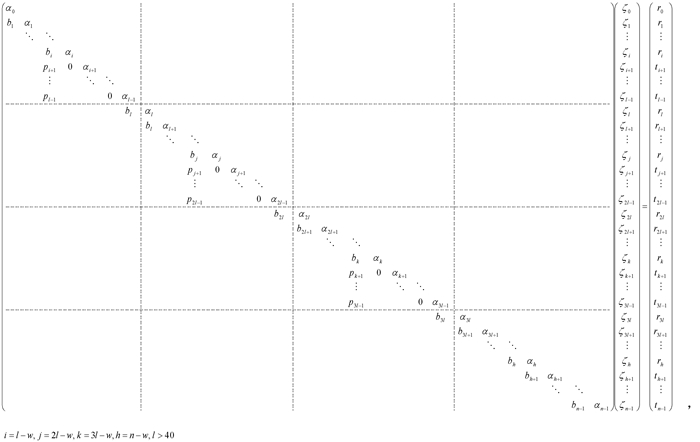
Stage 1) 以方程组(4)为例,if(ip<np){处理计算节点(ip+1)的关联方程组(由分配给计算节点ip的方程组的后w个方程组成),消去系数矩阵中相应的下次对角元素,并调整右端向量的相应元素,结果保存在临时缓冲区中: t(ip+1)l-w=r(ip+1)l-w,对(ip+1)l>f>(ip+1)l-w,tf=rf-(bf/αf-1)tf-1.这个过程引入填充项(fill-in) ${{p}_{f}}={{\left( -1 \right)}^{f-\left( {{i}_{p}}+1 \right)l+w}}{{b}_{\left( {{i}_{p}}+1 \right)l-w}}\prod\limits_{e=\left( {{i}_{p}}+1 \right)l-w}^{f-1}{{{b}_{e+1}}}/{{\alpha }_{e}}$.这里pf只是用于Stage 2推导填充项公式,在算法中不必计算. 对(ip+1)l>f>(ip+1)l-w,令τf=tf/αf,实际计算
|
(4) |
时采用如下公式: τ(ip+1)l-w=r(ip+1)l-w/α(ip+1)l-w,对(ip+1)l>f>(ip+1)l-w,τf=(rf-bfτf-1)/αf; 把τ(ip+1)l-1发送给计算节点 (ip+1). 这个阶段共需要w-1个乘法,w-1个减法和w个除法. }
Stage 2)以方程组(5)为例,if(ip>0){ 从计算节点(ip-1)接收数据τipl-1; 解分配给计算节点ip的方程组,消去系数矩阵中的下次对角元素,并调整右端向量的相应元素: ripl1=ripl-biplτipl-1; 对(ip+1)l>f>ipl,rf1=rf-(bf/αf-1)rf-11; 这个过程产生填充项 $p{{'}_{f}}={{\left( -1 \right)}^{f-{{i}_{p}}l+w}}{{b}_{{{i}_{p}}l-w}}\prod\limits_{e={{i}_{p}}l-w}^{f-1}{{{b}_{e+1}}}/{{\alpha }_{e}}$,$ \left( {{i}_{p}}+1 \right)l>f>{{i}_{p}}l-1$.对(ip+1)l>f>ipl-1,ζf=(rf1-p′fζipl-w-1)/αf,它依赖于ζipl-w-1; 如果|p′f |比较小,忽略p′fζipl-w-1,我们可以得到近似解ζ′f=rf1/αf,
|ζf-ζ′f|为误差. 如果w=20,对(ip+1)l>f>ipl-1,|ζf-ζ′f|<10-12|ζipl-w-1|.这里p′f只是用来估计误差,在算法中不必计算. 实际计算中采用如下算法: ζ′f=τipl-1,对(ip+1)l>f>ipl-1,ζ′f=(rf-bfζ′f-1)/αf.这个阶段共需要l个乘法,l个减法和l个除法.}
else if(ip=0){ζ′0=r0/α0,对l>f>0,ζ′f=(rf-bfζ′f-1)/αf.这个阶段计算ζ′f(l>f≥0)共需要l-1个乘法,l-1个减法和l个除法. }
以上描述了解方程组Lζ=r的并行算法. Lζ=r的近似解ζ′本文称为中间解.下面描述并行计算Ux′=ζ′的算法.
Stage 3) 以方程组(7)为例,if(ip>0){处理计算节点(ip-1)的关联方程组(由分配给计算节点ip的方程组的前w个方程组成),消去系数矩阵的上次对角元,并适当调整右端向量的相应元素,结果保存在临时缓冲区中: sipl+w-1=ζ′ipl+w-1;对ipl+w-1>f>ipl-1,sf=ζ′f-γfsf+1; 这个过程产生填充项 ${{q}_{f}}={{\left( -1 \right)}^{{{i}_{p}}l+w-1-f}}\prod\limits_{e={{i}_{p}}l+w-1}^{f}{{{\gamma }_{e}}}$,${{i}_{p}}l+w-1>f>{{i}_{p}}l-1$.这里qf只是用于Stage 4推导填充项公式,在算法中不必计算.把 sipl发送给计算节点(ip-1).实际算法中只需要计算sf(ipl+w-1>f>ipl-1),这个阶段共需要w-1个乘法和w-1个减法.}
Stage 4)以方程组(8)为例,if(ip<np-1){从计算节点(ip+1)接收s(ip+1)l,解分配给计算节点ip的方程组,消去系数矩阵中相应的上次对角元素,并适当调整右端向量: s′(ip+1)l=s(ip+1)l; 对(ip+1)l>f>ipl-1,
$
\left| {{\zeta }_{f}}-\zeta {{'}_{f}} \right|=\left| p{{'}_{f}} \right|\left| {{\zeta }_{{{i}_{p}}l-w-1}} \right|/\left| {{\alpha }_{f}} \right|<{{\left( 1/\left( 2+\sqrt{3} \right) \right)}^{w+1}}\left| {{\zeta }_{{{i}_{p}}l-w-1}} \right|,
$
(6)
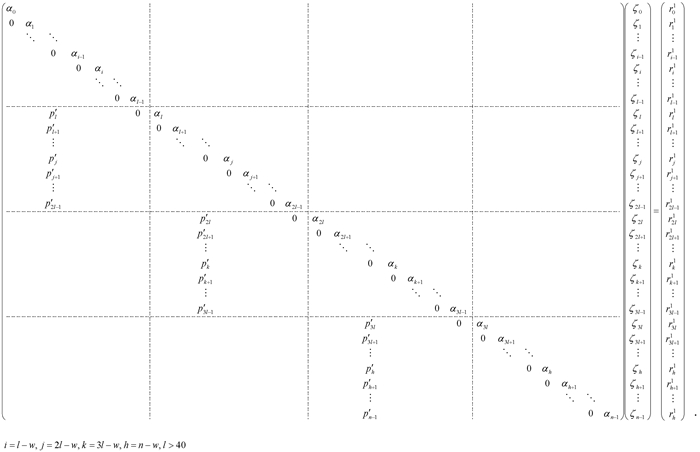
(5)
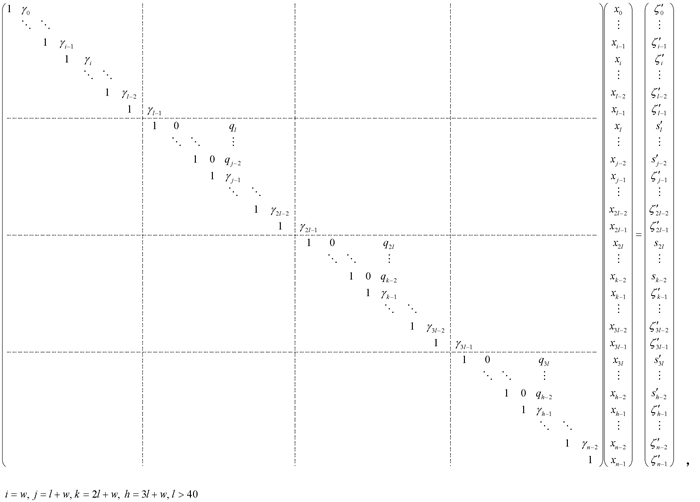
(7)
s′f=ζ′f-γfs′f+1.这个过程产生填充项 $q{{'}_{f}}={{\left( -1 \right)}^{\left( {{i}_{p}}+1 \right)l+w-1-f}}\prod\limits_{e=\left( {{i}_{p}}+1 \right)l+w-1}^{f}{{{\gamma }_{e}}}$,(ip+1)l>f>ipl-1.对(ip+1)l>f>ipl-1,x′f=s′f-q′fx′(ip+1)l+w,如果|q′f|比较小,忽略q′fx′(ip+1)l+w,我们有近似解,x″f=s′f.
(8)
| $ \left| x'{{'}_{f}}-x{{'}_{f}} \right|=\left| q{{'}_{f}}x{{'}_{\left( {{i}_{p}}+1 \right)l+m}} \right|<{{\left( 1/\left( 2+\sqrt{3} \right) \right)}^{w+1}}\left| x{{'}_{\left( {{i}_{p}}+1 \right)l+w}} \right|, $ | (9) |
else if(ip=np-1){s′npl-1=ζ′npl-1,对npl-1>f>(np-1)l-1,s′f=ζ′f-γfs′f+1;这一阶段共需要l-1个乘法和l-1个减法.}
该算法不必计算填充项,填充项只用来估计误差.根据式(6)和式(9),关联方程组的宽度w影响三对角方程组解的精度, w越大解越精确. w=20可以满足基本的精度要求,在实际应用中可以根据需要调整w.
采用这种方法,结点之间的数据交换次数远低于迭代方法.整个算法形式简单,计算量小,便于实现.以上给出解一个方程组的算法原理,事实上,每个方向上有许多扫描行,每个扫描行对应一个L方程组和一个U方程组,实际计算中需要采用上述算法先解这些L方程组,再解这些U方程组.
由于三维张量积B样条系数的反算可以分解成三个方向上1维 B样条系数的反算,在每个方向的计算中,计算节点之间需要传递虚网格数据.如图 2(上),以x方向9个计算节点为例,说明通信方式.每个中间节点需要两个通信,例如在“追”的过程中,中间节点需要从前一计算节点接收数据,又需要把数据发送给下一计算节点.这两个通信之间并无确定的顺序,当进行一个通信时,另一个通信必须等待,这样导致通信的依赖关系.在最坏的情况下,可能产生图 2(下)所示的通信依赖关系.
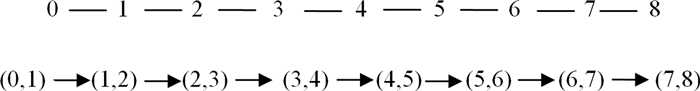 |
| 图2 x方向通信结构(上)和可能的通信依赖关系(下) Fig. 2 Communication topology in x direction(top) and dependence in communication(bottom) |
为了消除通信依赖关系,分两步进行通信,这样可以实现彻底的并行通信.如图 3(a)所示,在“追”的过程中本文采用如下的两步通信方法:
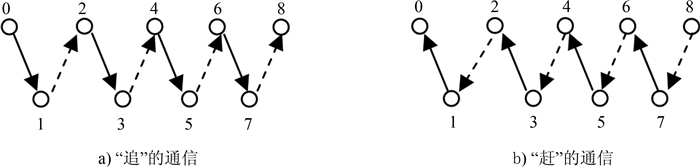 |
| 图3 两步通信算法 Fig. 3 Two steps communication algorithm |
step1)实线边并行通信:(0,1),(2,3),(4,5),(6,7);
step2)虚线边并行通信:(1,2),(3,4),(5,6),(7,8);
如图 3(b)所示,在“赶”过程中本文也采用两步通信方法.
采用两步通信方法,在每一步中,根据编号,结点两两成组,在组内进行通信.尽可能减少空闲结点,提高通信效率.如果计算节点数为奇数,每步各有1个空闲计算节点;如果计算节点数为偶数,第1步没有空闲计算节点,第2步有2个空闲计算节点.本文的通信结构为笛卡尔网格结构,如果各个方向计算节点较多,并行通信效率会较高.在实现时,进程之间通信采用MPI[18].
用Cuda实现Level Set演化方程的GPU解法器.在某个方向上,如果多于两个计算节点,采用多GPU混合并行方法.在沿该方向反算B样条系数时,相应扫描行之间具有独立性.这种独立性称为行独立性.因此具有并行性.每个计算节点在GPU上处理关联方程组和解所分配的方程组时,每个GPU线程可以计算一个扫描行,从而实现多线程并行计算.计算过程分为三个阶段:
phase1 如果必要用GPU处理关联方程组;
phase2 采用两步通信法传递数据;
phase3 解分配给本计算节点的方程组;
在有的方向上仅有一个计算节点,不需要多计算节点并行计算,不需要解关联方程组,这时,采用单GPU(多线程)方法解该方向的三对角方程组.该方向每个扫描行对应一个L方程组和一个U方程组.每个线程采用基于LU分解的追赶法解这些方程组.
在并行反算B样条系数之后,根据式(3)计算Φp+1,局部网格G中每个结点有独立性,称为网格结点独立性.如果每个网格结点都对应一个线程,这样对于大规模数据线程太多.因此,每个演化步的phase2,在GPU上采用多线程并行计算式(3),每个z扫描行分配给一个GPU线程,该线程对该扫描行的每个网格结点计算式(3).整个演化过程为:
for(p=0; p
沿z反算B样条系数;
沿y反算B样条系数;
沿x反算B样条系数;
根据式(3)计算Φp+1;
}
迭代步数n可以根据实际需要选取.
1.3 在并行演化过程中采用4阶Runge-Kutta方法为了提高演化精度,根据4阶Runge-Kutta的算法[17]思想改进演化方算法.如何把4阶Runge-Kutta的算法思想与具体的演化算法相结合,需要仔细考虑.
在下面的算法中,[·]表示对i=d,…,L+1; j=d,…,M+1; k=d,…,N+1执行括号中的操作·.
基本算法思想如下:Stage1 根据{Φi,j,kp},反算出 B 样条系数{ci,j,kp},得到 B 样条函数Φp;
[ki,j,k1=(H(Φp))i,j,k]; [Φi,j,kp+0.5=Φi,j,kp+ki,j,k1(0.5Δt)];
Stage2 根据{Φi,j,kp+0.5},反算B样条系数{ci,j,kp+0.5},得到B样条函数Φp+0.5;
[k2i,j,k=(H(Φp+0.5))i,j,k]; [Φp+0.5,2i,j,k=Φpi,j,k+k2i,j,k(0.5Δt)];
Stage3 根据{Φp+0.5,2i,j,k}反算B样条系数{cp+0.5,2i,j,k},得到B样条函数Φp+0.5,2;
[ki,j,k3=(H(Φp+0.5,2))i,j,k]; [Φi,j,kp+1,3=Φi,j,kp+ki,j,k3Δt];
Stage4 根据{Φi,j,kp+1,3}反算B样条系数{ci,j,kp+1,3},得到B样条函数Φp+1,3;
令[ki,j,k4=(H(Φp+1,3))i,j,k]; [Φi,j,kp+1= $ \frac{1}{6}$(ki,j,k1+2ki,j,k2+2ki,j,k3+ki,j,k4)Δt+Φi,j,kp];
把1.2节的并行算法应用到每一阶段,得到相应的并行算法.本文用Cuda实现了该算法. 2 测试结果算法在一个混合体系结构的Cluster上测试,每个计算结点上装有一个GPU,每个GPU有448个核. 在并行演化计算中采用双精度. 本文采用基于平均曲率的演化模型. 采用基于GPU的光线投射算法[19]绘制演化结果,以下测试中,如无特殊说明,关联方程组宽度w=20.
图 4(a)是MRI_head初始数据,大脑皮层不清晰;图 4(b)经过基于平均曲率的演化,去除噪声,可以清楚地看到大脑皮层. 图 4(c)并行计算时,每个计算节点单独计算,不考虑结点之间的依赖关系,MRI_Head演化结果有缝隙.图 4(d)并行计算时,考虑结点之间的依赖关系,采用基于LU分解的并行追赶法,MRI_Head演化结果无缝隙.
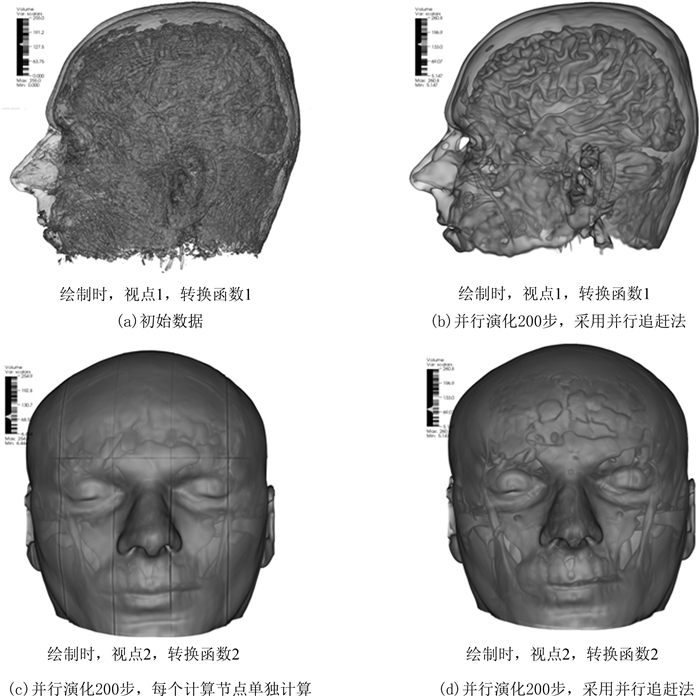 |
| 图4 MRI_Head 256×256×256数据 Fig. 4 MRI_Head 256×256×256 dataset |
图 5(a)是Pine_root初始数据,噪声很多,看起来象碎屑,不象树根.图 5(c)是并行演化结果,看起来更象树根. 图 5(b)并行计算,每个计算节点单独计算,不考虑结点之间的依赖关系,Pine_root演化结果有缝隙.图 5(c)并行计算,考虑结点之间的依赖关系,采用基于LU分解的并行追赶法,Pine_root演化结果无缝隙.
 |
| 图5 Pine_root 256×256×256数据 Fig. 5 Pine_root 256×256×256 dataset |
由图 4,图 5可见,本文的并行演化算法可以去除噪声,恢复物体的本来特征,并且可以消除缝隙.
图 6(a)给出XMas_Tree初始数据的绘制结果.图 6(b)给出XMas_Tree演化100步的结果,许多特征得到光顺,结果中没有缝隙.
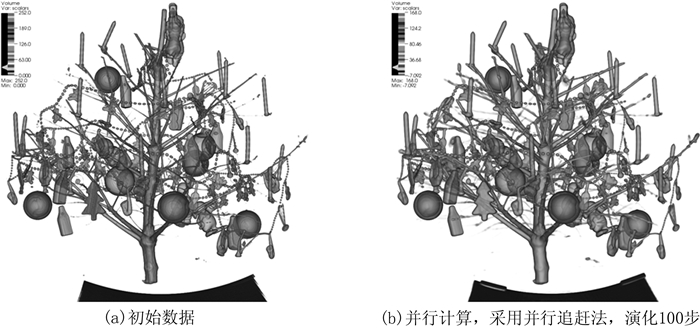 |
| 图6 XMas_Tree512×512×999数据 Fig. 6 XMas_Tree512×512×999 dataset |
图 7给出用36个计算节点对MRI_Head演化10 000步的结果.图 7(a)未采用Runge-Kutta方法,演化时间379.7秒.图 7(b)采用Runge-Kutta方法,对MRI_Head演化10 000步,演化时间1 599.9秒.图像略有差别,计算精度不同.
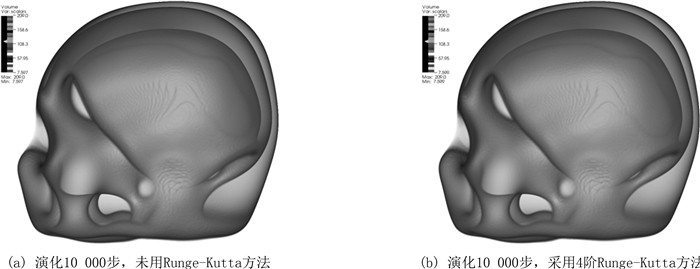 |
| 图7 MRI_Head 256×256×256数据,结果2 Fig. 7 MRI_Head 256×256×256 dataset, Result 2 |
本文称缓冲式发送和阻塞式接收的通信方法为单步法.图 8给出对数据XMas_Tree512×512×999,Z向“追”的过程,20计算节点采用单步法和本文两步法的通信时间.由图 8可见,在节点18和节点19上两种方法通信时间相当.在其余节点上,本文的两步通信法快于单步法.
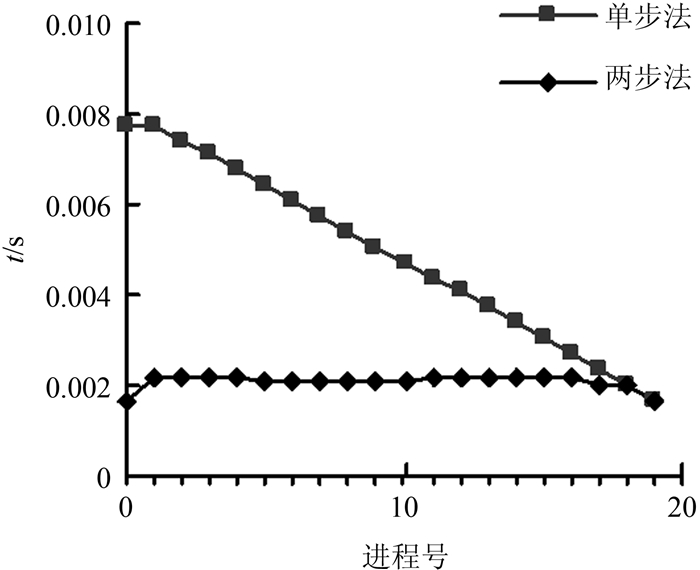 |
| 图8 Z向“追”的过程通信时间 Fig. 8 Communication time of elimination in Z |
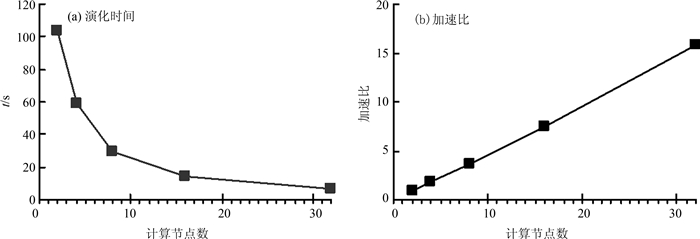 |
| 图9 MRI_Head数据并行演化的时间和加速比 Fig. 9 Time and speedup for parallel evolution of MRI_Head dataset |
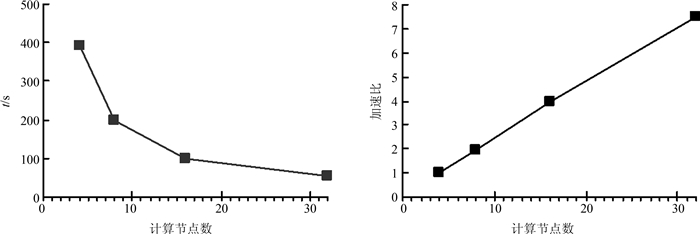 |
| 图10 XMas_Tree数据并行演化的时间和加速比 Fig. 10 Time and speedup for parallel evolution of XMas_Tree dataset |
图 9给出了MRI_Head256×256×256数据并行演化200步的时间和加速比.测试时,以2节点并行计算为基准.图 10给出了XMas_Tree512×512×999数据并行演化100步的时间和加速比,测试时,以4节点并行计算为基准.由图 9,图 10可见随着结点数的增加,计算时间减少,加速曲线几乎呈直线,并行方法是有效的,具有很好的可扩展性.
3 结论在数据场演化过程中,采用张量积B样条函数和4阶Runge-Kutta方法提高演化精度.采用张量积B样条函数把三维相关性转化为一维相关性,提高了并行度.实现了基于精确LU分解的高精度并行追赶法,该方法不必计算Spike,分割数据时不必交叠;采用两步通信方法,消除通信的依赖关系,实现有效的并行通信.在此基础上,实现Level Set并行高精度演化.实验结果表明,本文的并行算法是有效的.
| [1] | NVIDIA.NVIDIA_CUDA_Programming_Guide[CP/OL].[2015-03-09]http://docs.nvidia.com/cuda/pdf/CUDA_C_Programming_Guide.pdf. |
| [2] | HOWISON M, BETHEL E W, CHILDS H. Hybrid parallelism for volume rendering on large-, multi-, and many-core systems[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(1):17-29. |
| [3] | OSHER S, SETHIAN J. Fronts propagating with curvature dependent speed:Algorithms based on Hamilton-Jacobi formulation[J]. Journal of Computational Physics, 1988,79(1):12-49. |
| [4] | ROSENFELD A. Edge and curve detection for visual scene anaIysis[J]. IEEE Transactions on Computers, 1971, 20(5):562-569. |
| [5] | WITKIN A P. Scale-space filtering[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing 1984, Piscataway,NJ,USA:IEEE Press,1984:150-153. |
| [6] | PERONA P, MALIK J. Scale space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639. |
| [7] | ALVAREZ L, LIONS P L MOREL J M. Image selective smoothing and edge detection by nonlinear diffusion.Ⅱ[J]. SIAM Journal on Numerical Analysis,1992,29(3):845-866. |
| [8] | CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision,1997,22(1):61-79. |
| [9] | RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D Nonlinear Phenomena, 1992, 60(1/4):259-268. |
| [10] | UNSER M, ALDROUBI A, EDEN M. On the asymptotic convergence of B-spline wavelets to Gabor functions[J]. IEEE Transactions on Information Theory,1992, 38(2):864-872. |
| [11] | BRINKS R. On the convergence of derivatives of B-splines to derivatives of the Gaussian function[J]. Computational &Applied Mathematics,2008, 27(1):79-92. |
| [12] | de BOOR C. On calculation with B-spline[J].Journal of Approximation Theory,1972,6(1):50-62. |
| [13] | COX M G.The numerical evaluation of B-spline[J].IMA Journal of Applied Mathematics,1972,10(2):134-149. |
| [14] | 施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:北京航空航天大学出版社,1994. |
| [15] | LARRIBA-Pey J L, NAVARRO J J, JORBA A, et al. Review of general and toeplitz vector bidiagonal solvers[J]. Parallel Computing, 1996, 22(8):1091-1126. |
| [16] | 崔锦泰. 小波分析导论[M].程正兴,译.西安:西安交通大学出版, 1994. |
| [17] | 何旭初,苏煜成,包雪松. 计算数学简明教程[M]. 北京:高等教育出版社, 1980. |
| [18] | 莫则尧,袁国兴.消息传递并行编程环境[M].北京:科学出版社,2001. |
| [19] | 袁斌.改进的均匀数据场GPU光线投射[J].中国图象图形学报,2011,16(7):1269-1275. |
引用本文 |
 2016, Vol. 33
2016, Vol. 33
