| First-Principles Study of Electronic and Optical Properties of BxGa1-xAs Alloy |
2. Shanxi University, Taiyuan 030006, China
2. 山西大学, 太原 030006
Boron-containing Ⅲ-V alloys are promising semiconductor materials for potential applications in the field of band-gap and strain engineering as well as optoelectronic integration. Recently, incorporation of boron into GaAs and InGaAs has attracted more and more attention, which could provide a possible way to develop high-efficiency solar cells or detectors on GaAs substrates. On the other hand, incorporation of boron can reduce strain accumulation in highly-strained InGaAs/GaAs and GaAsSb/GaAs multiple quantum wells[1-6]. Despite the importance of BGaAs alloy, many basic properties have not been studied yet, due to the difficulty in synthesizing BGaAs alloy. Epitaxial growth of Bx Ga1-xAs has been realized by metalorganic chemical vapor deposition (MOCVD) and molecular-beam epitaxy (MBE). But, boron concentration x in Bx Ga1-xAs is still very low (x≤8%)[7-8]. Moreover, the optical properties of BGaAs alloy have been rarely reported so far. However, properties of BGaAs have played a great role in the fabrication of BGaAs-based devices. Theoretical calculations for boron incorporation behaviors and the physical properties of Bx Ga1-xAs alloy are urgently demanded.
In this study, using first-principles calculation, we investigate structural, electronic and optical properties of Bx Ga1-xAs alloy. The goal of this work is to get physical properties of BGaAs and to provide better insight into this promising material.
1 Computational methodsCalculations are preformed using density functional theory (DFT) within the local density approximation (LDA) in CASTEP simulation package[9-10]. The Brillouin zone is sampled with Monkhorst-Pack scheme (4×4×4 mesh). The Coulomb potential energy caused by electron-ion interaction is described using ultra-soft scheme[11]. B (2s22p1), Ga (3d104s24p1) and As (4s24p3) electrons are treated as valence electrons. Experimental lattice constants of GaAs were employed as an initial input geometry. The energy cutoff for plane wave expansion of the wave functions is 400 eV, which gives energy convergence less than 5×10-7eV. A more efficient special quasirandom structure (SQS) approach is employed to describe the random alloy, which has been used extensively to study electronic and thermodynamics properties of random alloys[12-14]. The SQS is designed so that the physically most relevant atom-atom correlation function of the SQS is closest to the random substitutional alloy within a finite supercell. Bx Ga1-xAs alloy is modeled with 64-atom SQS corresponding to 2×2×2 conventional cubic cells at x=0.062 5, 0.25, 0.5, 0.75 and 0.937 5.
2 Results and discussions 2.1 Structural propertiesThe structural properties of Bx Ga1-xAs alloy are calculated using optimized atomic positions at the equilibrium volumes. Our calculated lattice constant for GaAs and BAs are 5.574 7Åand 4.683 7Å. They are in good agreement with experimental and other theoretical results[15-16]. This indicates that the model and parameters are reasonable. Figure 1 shows calculated equilibrium lattice constant as a function of boron composition x. The solid line represents a linear interpolation of the Vegard's law and the pentacles represent the lattice constant obtained from DFT simulations. The lattice constant calculated by LDA is greater than the Vegard's law. A small deviation from Vegard's law is noticed. The magnitude of deviation can be attributed to the quality of description of interaction between the valence electrons and the ionic core. Physical origin of the deviation should be the change of bond energy and bond lengths that show relaxation from their ideal positions. The calculated bond lengths of RGaAs and RBAs are 2.413 9Åand 2.081 0Å, respectively. They are similar results of other calculations[17-18]. Figure 2 shows calculated average bond lengths of RB-As and RGa-As in Bx Ga1-x As as functions of composition x. In detail, there is an inward relaxation in GaAs by boron incorporation. It indicates a significant structural relaxation of RB-As and RGa-Asdue to the large discrepancy between atomic sizes of Ga and B ions. We notice that the bond lengths reveal a weak linear dependence on the alloy composition.
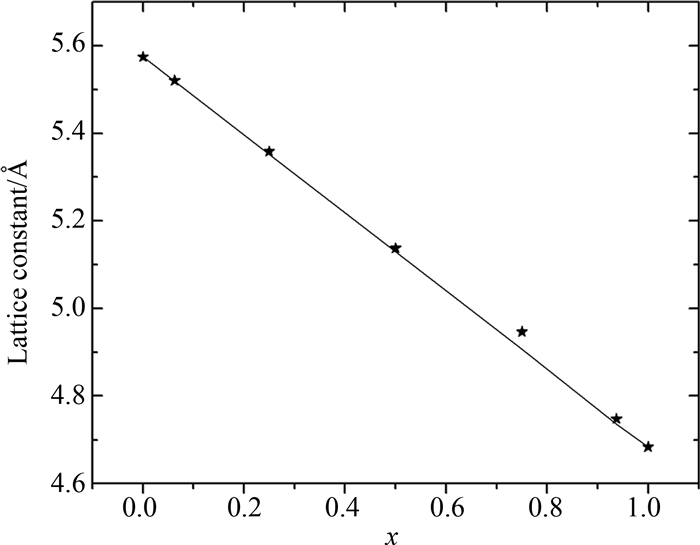 |
| Fig.1 Vegard's law and LDA calculated lattice constant of BxGa1-xAs. |
 |
| Fig.2 Calculated bond lengths of BxGa1-xAs alloy at different composition |
The bong-length and bond-angle distribution cause strain energy equal to the mixing enthalpy, which depends on the size of lattice mismatch of the alloy. Mixing enthalpy of Bx Ga1-xAs alloy can be estimated as
| $ \Delta H\left( x \right) = {E_{{{\rm{B}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}{\rm{As}}}} - x{E_{{\rm{BAs}}}} - \left( {1 - x} \right){E_{{\rm{GaAs}}}}, $ | (1) |
where EBxGa1-xAs, EBAs and EGaAs are calculated total energies of Bx Ga1-xAs, BAs and GaAs, respectively. Figure 3 shows the calculated mixing enthalpies of Bx Ga1-xAs at different composition x. ΔH can be expressed as a function of x by a third-order polynomial, ΔH=ωx(1-x). ω is a composition-dependent interaction parameter, which is related to the binding energy. By fitting the calculated formation enthalpies we obtained ω=(431.909x+384.642) meV·atom-1.
 |
| Fig.3 Calculated mixing enthalpy of BxGa1-xAs as a function of composition x |
A greater ΔH implies higher strain energy and critical temperature. According to general alloy theory[19], Gibbs free energy of mixing of an alloy is
| $ \Delta {\rm{G = }}\Delta H - T\Delta S. $ | (2) |
The entropy of mixing is assumed
| $ \Delta S = - {k_{\rm{B}}}\left[ {x\ln x + \left( {1 - x} \right)\ln \left( {1 - x} \right)} \right]. $ | (3) |
The temperature-composition phase diagram is shown in Fig. 4. The solid and dashed curves correspond to the binodal and the spinodal decomposition lines, respectively. The binodal curve is constructed using a common tangent approach. A miscibility gap exists between two binodal points. The spinodal curve is determined from the inflection points where ∂2ΔG/∂x2=0. We can draw the region of metastability from the spinodal curve. The calculated phase diagram shows a wide and asymmetric miscibility gap. In detail, e.g., at T=2 000 K, we predict a miscibility gap in a range 0.109≤x≤0.991. The critical temperature for phase separation is about 4 214.23 K at x=0.67. The miscibility gap disappears and a homogeneous random alloy is predicted above the critical temperature and composition.
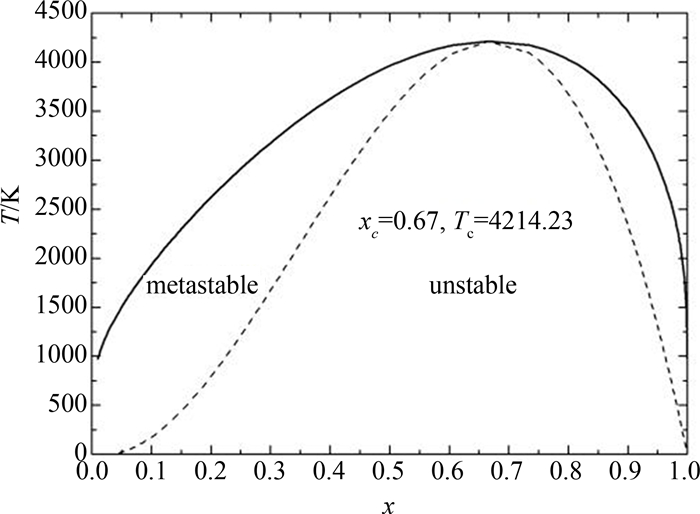 |
| Fig.4 Temperature-composition phase diagram of BxGa1-xAs |
We predicted the band structure of the alloy along high directions in the first Brillouin zone at the optimized lattice constant. Band gaps Eg of Bx Ga1-xAs alloy can be extracted from the following equation
| $ {E_g}\left( x \right) = \left( {1 - x} \right){E_{\rm{g}}}\left( {{\rm{GaAs}}} \right) + x{E_{\rm{g}}}\left( {{\rm{BAs}}} \right) - bx\left( {1 - x} \right). $ | (4) |
Deviation of Eg is characterized by the bowing parameter b. GaAs is a direct band gap (Γ-Γ) semiconductor. BAs has an indirect band gap along Γ-X direction. It is well known that the LDA systematically underestimates the band gap, but effect on accuracy of the bowing parameter is small. The LDA band gap error is canceled in deriving the bowing parameters[20-21]. Calculated band structures at x=6.25% and 25% are shown in Fig. 5 and Fig. 6, respectively. It shows that Bx Ga1-xAs alloy are direct band gap at x=6.25% and 25%. Since boron substitution breaks symmetry of the structure, there is no well-defined method to unfold band structure into the Brillouin zone of the primitive 2-atom zinc-blende unit cell, which does not allow us to distinguish between direct and indirect band gap at x=0.5 and 0.75. The direct character of the gap makes the crystal suitable for laser light generation.
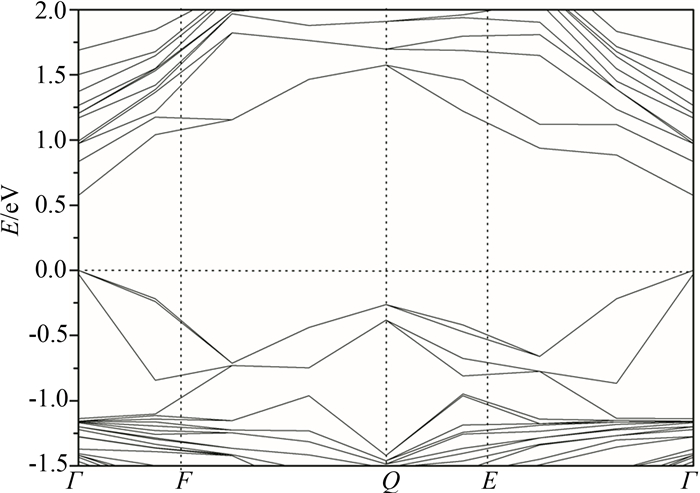 |
| Fig.5 Calculated band structures of BxGa1-xAs at x=6.25% |
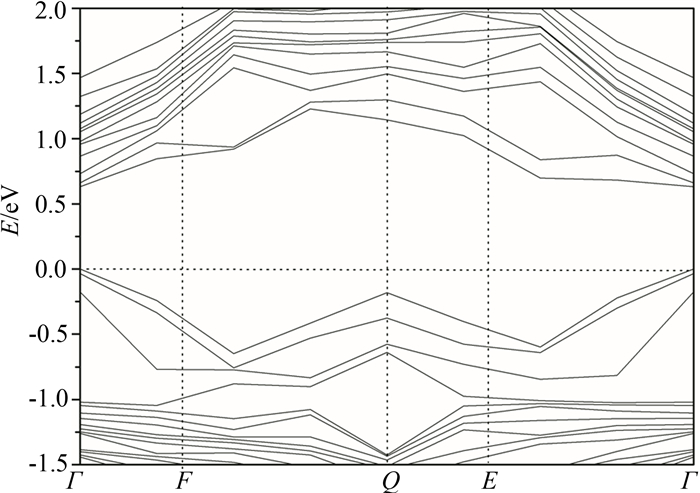 |
| Fig.6 Calculated band structures of BxGa1-xAs at x=25% |
The calculated band-gap results are corrected by applying a band-gap shift of the composition. Nonlinearity in the band-gap is due to volume deformation, charge transfer, as well as bond length relaxation. Direct band-gap of the alloy is obtained with experimental band gap of GaAs, GW-estimated value for BAs[22] and calculated bowing parameters. The band gaps indicate that the alloys are suitable for applications in infrared region and can be used to filter certain wavelengths. The results (Table. 1) show that BxGa1-xAs alloy has relatively small bowing parameters. The bowing parameters have a weak dependence on boron composition. Experimental data estimate a bowing parameter of (2.3±0.3) eV (x≤3%)[1]. Shan et al found a small increase (14 meV) of band gap with boron composition up to 3% experimentally[23]. Saidi et al show that the band gap of Bx Ga1-xAs increases slowly as the boron content increases (x≤7%)[24]. We notice that incorporation of a small boron (x≤6.25%) does not induce a significant change (17 meV) in band gap energy which is associated with the small bowing parameter. The trend is in good agreement with experimental data.
| Table 1 Direct band-gap and bowing parameter of BxGa1-xAs alloy at different boron composition |
 |
| Click to enlarge |
We now turn to optical properties of GaAs and BGaAs. We chose composition x=6.25% as a representative example for comparison. Interaction between photons and electrons can be described by the dielectric function ε(ω)=ε1(ω)+iε2(ω). The real part ε1(ω) is obtained by Kramers-Kronig relation. All optical properties, including absorption coefficient α(ω), reflectivity R(ω), refractive index n(ω) and energy loss spectrum L(ω) that are important for optical materials and related applications are studied.
Imaginary parts of the dielectric functions of GaAs and BGaAs are displayed in Fig. 7. ε2(ω) of GaAs show a strong peak at 4.2 eV and a small peak around 2.7 eV, which have red shifts of 0.6 eV and 0.4 eV from the experimental values, respectively[25]. This deviation may be related to the overestimation of momentum matrix elements and the neglection of excitonic effect. The absorption coefficient spectra are shown in Fig. 8. The prominent peaks occur at about 4.8 eV and 4.5 eV for GaAs and BGaAs. The absorption edge shifts towards lower energy as B is incorporated which reduces the transparency region of the alloy.
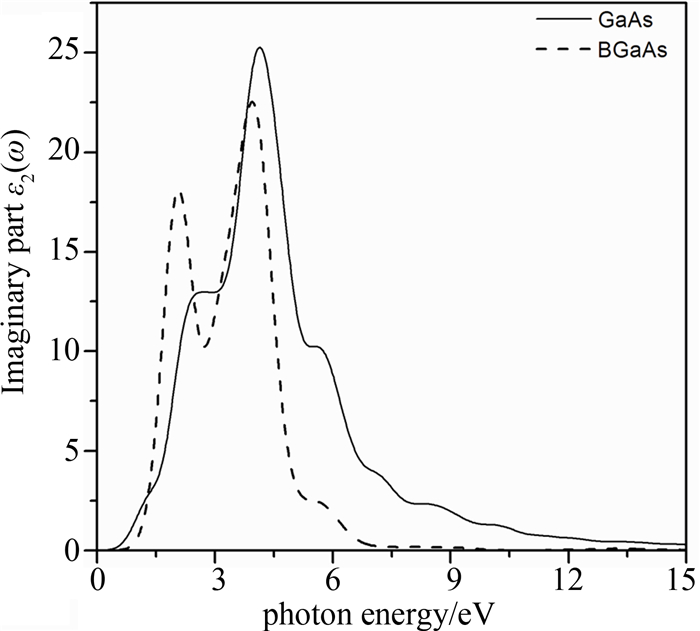 |
| Fig.7 Imaginary parts ε2 of dielectric functions of GaAs and BxGa1-xAs at x=6.25% |
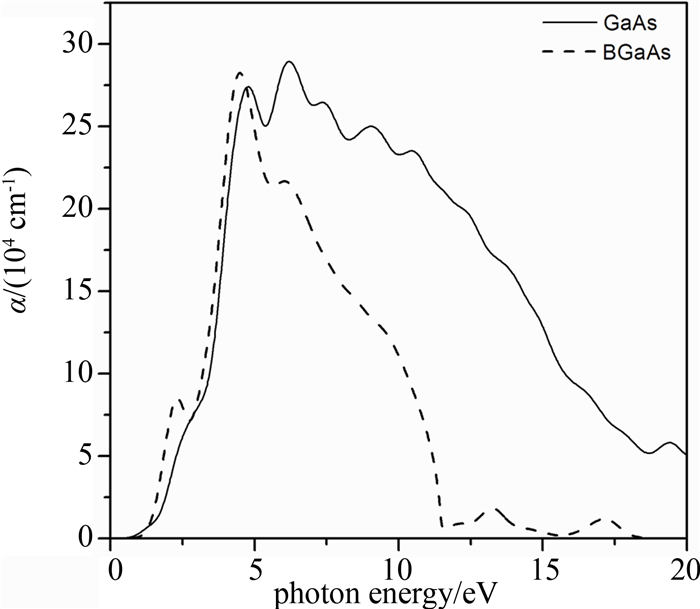 |
| Fig.8 Absorption coefficients spectrum of GaAs and BxGa1-xAs at x=6.25% |
Finally, reflectivity, refractive index and energy loss function were obtained (as shown in Fig. 9). The maximum peak with high reflectivity of BGaAs occurs in the energy range between 7 eV and 11 eV, while R(ω) of GaAs is small in this range. The refractive index is an important optical design parameter, such as distributed Bragg reflectors. We find n(0) of the alloy is lower than that of GaAs. n(ω) of GaAs is higher than that of BGaAs in low energy range with an exception of a shoulder around 1.7 eV for BGaAs and decreases with the increase of photon energy in the energy range of 3.6 eV-11 eV. The energy loss function is an important parameter describing energy loss of a fast electron traversing in a material. Its main peak is so called plasma frequency. There is no distinct peak in the range of 0-11 eV since the imaginary part is still large at these values. The peaks for GaAs and BGaAs are about 16.1 eV with a very broad peak and 11.4 eV with an especially clear peak and very narrow maximum. These peaks correspond to slow and rapid reduction of respective reflectivity[26].
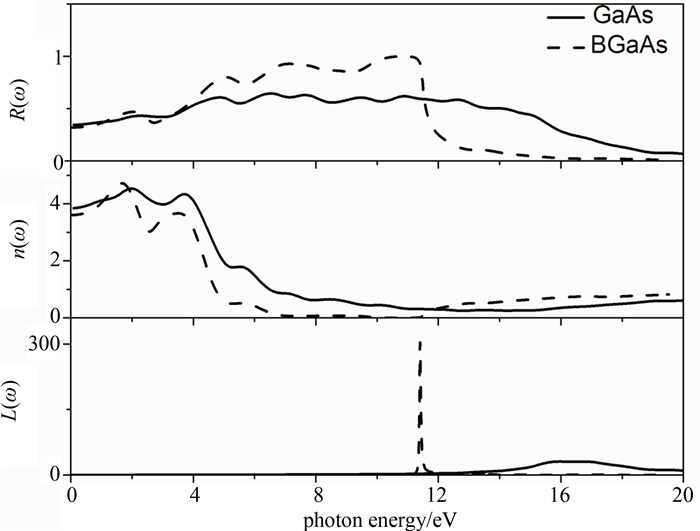 |
| Fig.9 Reflectivity, refractive index and energy loss functions of GaAs and BxGa1-xAs at x=6.25% |
In this work we studied structural, electronic and optical properties of Bx Ga1-xAs alloy with first-principles density-functional calculations. The lattice constant and internal parameters are optimized. The lattice constant of Bx Ga1-xAs exhibit a small deviation from the Vegard's law and the bond lengths reveal significant relaxations. The bowing coefficient is found small (2.57 eV-5.01 eV) and weakly composition-dependent. Finally, optical properties of the alloy are presented, which indicate that incorporation of boron can have significant effects on optical properties. The absorption edge has a significantly red shift compared to GaAs. The alloy is suitable for optical devices. Our results are helpful for further research.
| [1] | GEISZ J F, FRIEDMAN D J, OLSON J M, et al. BGaInAs alloys lattice matched to GaAs[J]. Appl Phys Lett , 2000, 76 (11) :1443–1445. doi:10.1063/1.126058 |
| [2] | GOTTSCHALCH V, LEIBIGERA G, BENNDORF G. MOVPE growth of BxGa1-xAs, BxGa1-x-yInyAs and BxAl1-xAs alloys on (001) GaAs[J]. J Cryst Growth , 2003, 248 :468–473. doi:10.1016/S0022-0248(02)01870-5 |
| [3] | WANG Q, REN X M, HUANG H, et al. Growth of BxGa1-xAs, BxAl1-xAs and BxGa1-x-yInyAs epilayers on (001) GaAs by low pressure metalorganic chemical vapor deposition[J]. Microelectron J , 2009, 40 (1) :87–91. doi:10.1016/j.mejo.2008.06.066 |
| [4] | WANG Q, JIA Z G, REN X M, et al. Effect of boron incorporation on the structural and photoluminescence properties of highly-strained InxGa1-xAs/GaAs multiple quantum wells[J]. AIP Adv , 2013, 3 (7) :072111(1-13). |
| [5] | HAMILA R, SAIDI F, MAAREF H, et al. Photoluminescence properties and high resolution X-ray diffraction investigation of BInGaAs/GaAs grown by the metalorganic vapour phase epitaxy method[J]. J Appl Phys , 2012, 112 (6) :063109(1-5). |
| [6] | JIA Z G, WANG Q, REN X M, et al. LP-MOCVD growth of BGaAsSb thick layers and BGaAsSb/GaAs quantum well structures on GaAs (001) substrates[J]. Journal of Crystal Growth , 2014, 394 :74–80. doi:10.1016/j.jcrysgro.2014.02.017 |
| [7] | HAMILA R, SAIDI F, RODRIGUEZ P H, et al. Growth temperature effects on boron incorporation and optical properties of BGaAs/GaAs grown by MOCVD[J]. J Alloys Compd , 2010, 506 (1) :10–13. doi:10.1016/j.jallcom.2010.06.169 |
| [8] | PTAK A J, BEATON D A, MASCARENHAS A. Growth of BGaAs by molecular-beam epitaxy and the effects of a bismuth surfactant[J]. J Cryst Growth , 2012, 351 (1) :122–125. doi:10.1016/j.jcrysgro.2012.04.026 |
| [9] | PERDEW J P, ZUNGER A. Self-interaction correction to density-functional approximations for manyelectron systems[J]. Phys Rev B , 1981, 23 (10) :5048–5078. doi:10.1103/PhysRevB.23.5048 |
| [10] | SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-principles simulation:ideas, illustrations and the CASTEP code[J]. J Phys Condens Matter , 2002, 14 (11) :2717–2744. doi:10.1088/0953-8984/14/11/301 |
| [11] | FURTHMULLER J, KACHELL P, BECHSTEDT F. Extreme softening of Vanderbilt pseudopotentials:General rules and case studies of first-row and d-electron elements[J]. Phys Rev B , 2000, 61 (7) :4576–4587. doi:10.1103/PhysRevB.61.4576 |
| [12] | ZUNGER A, WEI S H, FERRIRA L G, et al. Special quasirandom structures[J]. Phys Rev Lett , 1990, 65 (3) :353–356. doi:10.1103/PhysRevLett.65.353 |
| [13] | SHIN D, Van de WALLE A, WANG Y, et al. First-principles study of ternary fcc solution phases from special quasirandom structures[J]. Phys Rev B , 2007, 76 (14) :144204(1-10). |
| [14] | PEZOLD J V, DICK A, FRIAK M, et al. Generation and performance of special quasirandom structures for studying the elastic properties of random alloys:Application to Al-Ti[J]. Phys Rev B , 2010, 81 (9) :094203(1-7). |
| [15] | VURGAFTMAN I, MEYER J R, RAM-MOHAN L R. Band parameters for III-V compound semiconductors and their alloys[J]. J Appl Phys , 2001, 89 (11) :5815–5865. doi:10.1063/1.1368156 |
| [16] | WANG S Q, YE H Q. Plane-wave pseudopotential study on mechanical and electronic properties for IV and III-V crystalline phases with zinc-blende structure[J]. Phys Rev B , 2002, 66 (23) :235111(1-7). |
| [17] | HART G L W, ZUNGER A. Electronic structure of BAs and boride III-V alloys[J]. Phys Rev B , 2000, 62 (20) :13522–13537. doi:10.1103/PhysRevB.62.13522 |
| [18] | KOMSA H P, AROLA E, et al. Beryllium doping of GaAs and GaAsN studied from first principles[J]. Phys Rev B , 2009, 79 (11) :115208(1-9). |
| [19] | CHEN A B, SHER A. Semiconductor alloys:Physics and material engineering[M]. New York: Plenum Press , 1995 : 67 -86. |
| [20] | WEI S H, ZUNGER A. Giant and composition-dependent optical bowing coefficient in GaAsN alloys[J]. Phys Rev Lett , 1996, 76 (4) :664–667. doi:10.1103/PhysRevLett.76.664 |
| [21] | WEI S H, ZHANG S B, ZUNGER A. First-principles calculation of band offsets, optical bowings, and defects in CdS, CdSe, CdTe and their alloys[J]. J Appl Phys , 2000, 87 (3) :1304–1311. doi:10.1063/1.372014 |
| [22] | SURH M P, LOUIE S G, COHEN M L. Quasiparticle energies for cubic BN, BP, and BAs[J]. Phys Rev B , 1991, 43 (11) :9126–9132. doi:10.1103/PhysRevB.43.9126 |
| [23] | SHAN W, WALUKIEWICZ W, WU J, et al. Band-gap bowing effects in BxGa1-xAs alloys[J]. J Appl Phys , 2003, 93 (5) :2696–2699. doi:10.1063/1.1540230 |
| [24] | SAIDI F, HASSEN F, MAAREF H, et al. Optical study of BxGa1-xAs/GaAs epilayers[J]. Mater Sci Eng C , 2006, 26 (2-3) :236–239. doi:10.1016/j.msec.2005.10.056 |
| [25] | ASPNES D E, STUDNA A A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1. 5 to 6. 0 eV[J]. Phys Rev B , 1983, 27 (2) :985–1009. doi:10.1103/PhysRevB.27.985 |
| [26] | SUN J, WANG H T, HE J L, et al. Ab initio investigations of optical properties of the high-pressure phases of ZnO[J]. Phys Rev B , 2005, 71 (12) :125132(1-5). |
 2016, Vol. 33
2016, Vol. 33

