| mBBM方程的双扭结孤立波及其动力学稳定性 |
2. 甘肃民族师范学院 物理与水电工程系, 合作 747000
2. College of Physics and Hydropower Engineering, Gansu Normal University For Nationalitles, Hezuo 747000, China
1972年, Benjamin, Bona和Mahony在研究非线性水波时提出了Benjamin-Bona-Mahony (BBM)方程[1].该方程是描述弱非线性色散介质中非线性波单向传播的重要模型[2], 也出现在双温导热问题、岩石裂缝中的渗流问题等的研究中[3].如果非线性效应增强, 可得到如下Modified Benjamin-Bona-Mahony (mBBM)方程[4]
| $ {u_t} + {u_x} + {u^2}{u_x} + \alpha {u_{xxt}} = 0, $ | (1) |
其中α为色散系数.方程(1)是一典型的非线性偏微分方程, 有许多行之有效的方法可对这类方程进行求解, 如指数函数展开法[5]、F-展开法[6-8]、双曲函数法[9-13]、齐次平衡法[14]、假设法[15]等, 其中很多方法可利用Mathematica等计算机代数系统实现机械化计算.对数学物理方程来讲, 新解往往预示着新的物理现象, 所以对非线性偏微分方程的解进行研究可加深对物理现象本质特征的认识.
本文首先用双曲函数展开法求解方程(1), 得到四类孤立波解, 其中一类具有双扭结状结构.就我们所知, 目前尚无mBBM方程此类孤立波的相关报道.对孤立波的结构特征分析后发现该孤子在不同的极限情况下, 分别退化为扭结型孤立波或钟型孤立波.然后构造有限差分格式对双扭结状孤子的长时间动力学行为进行数值模拟, 该格式为两层隐式格式, 在线性化意义下绝对稳定.数值结果表明: mBBM方程描述的双扭结状孤子在各种不同类型的扰动下均稳定, 表现出很强的抗干扰性.这种稳定性很强的孤立波有利于实验观测.对双孤立波的碰撞过程进行数值模拟, 发现既存在弹性碰撞也存在非弹性碰撞.
1 mBBM方程的孤立波解及其结构特征双曲函数展开法[9]是一种求解非线性演化方程孤立波解的有效方法, 现已广泛用于很多方程的研究中.文献[10-11]中对该方法进行了扩展, 发现了mKdV与cKdV方程的一种具有新型结构的孤立波解.文献[12]采用扩展后方法求解了耦合KdV方程组, 发现其一组解存在双峰状或双扭结状的孤立波结构.是否其它非线性演化方程也具有这种新型结构的孤立波解呢?本文采用文献[10-12]中扩展的双曲函数展开法对mBBM方程(1)进行求解, 得到了四种类型的孤立波解.我们注意到mBBM方程也具有双扭结状孤立波解.数值模拟表明该结构的孤立波有很强的抗干扰性, 表现出很强的动力学稳定性.
双曲函数展开法在相关文献中有详细论述, 在此简述如下.对于方程, 比如两个独立变量x, t,
| $ K\left( {u,{u_t},{u_{xx}}, \cdots } \right) = 0 $ | (2) |
考虑其行波解
| $ u\left( {x,t} \right) = \phi \left( \xi \right),\;\;\;\;\;\;\xi {\rm{ = }}kx - \omega t + {x_0}. $ | (3) |
可将方程(2)化为关于ϕ的常微分方程(Ordinary Differential Equation, ODE).假设其解为
| $ \phi = \sum\limits_{i = 0}^M {{a_i}{f^i}} {\rm{ + }}\sum\limits_{j = 1}^M {{b_j}{f^{j - 1}}g} , $ | (4) |
其中f=f(ξ), g=g(ξ)称为展开函数, a0, ai, bi(i=1, 2, …, M)为待定系数; 通过平衡ODE的最高阶微分项和非线性项的阶数确定M.把(4)式代入ODE并利用f与g之间的关系式, 使得所得方程的各项中只含有f和g的幂次项且g的幂次不大于1.合并f和g的同次幂项并取其系数为零, 就得到包含所有待定常数的非线性代数方程组(Nonlinear Algebraic Equation System, NAES).求解此NAES (可借助计算机代数系统如Maple、Mathematica等完成)可以确定所有待定系数a0, ai, bi(i=1, 2, …, M)以及k, ω,从而最终得到方程(2)的精确解.
本文选择展开函数为文献[10-11]中所用的扩展的双曲函数.为书写方便, 我们将双曲函数转化为指数函数形式, 并记
| $ f\left( \xi \right) = 2/\left( {2r + {{\rm{e}}^\xi } + p{{\rm{e}}^{-\xi }}} \right), g\left( \xi \right) = \left( {{{\rm{e}}^\xi }-p{{\rm{e}}^{-\xi }}} \right)/\left( {2r + {{\rm{e}}^\xi } + p{{\rm{e}}^{ - \xi }}} \right), $ |
其中r, p为常数.下面列出用该方法得到的mBBM方程的4类精确解而略去详细的求解过程.后面讨论相关结果时, 也仅在实数范围内考虑并一律假定k≠0.
类型1
| $ u\left( {x,t} \right) = {\varepsilon _1}\sqrt {\frac{{3{k^2}\alpha \left( {{r^2} - p} \right)}}{{2 - {k^2}\alpha }}} f\left( \xi \right) + {\varepsilon _2}\sqrt k \sqrt \alpha \sqrt {\frac{{3k}}{{2 - {k^2}\alpha }}} g\left( \xi \right), $ | (5) |
其中,ε12=ε22=1,ω=2k/(2-k2α).若要求该解为实函数, 则应α>0,
类型2
| $ u\left( {x,t} \right) = \pm \sqrt k \sqrt \alpha \sqrt {\frac{{6k}}{{1 - 2{k^2}\alpha }}} \frac{{{{\rm{e}}^\xi } - p{{\rm{e}}^{ - \xi }}}}{{{{\rm{e}}^\xi } + p{{\rm{e}}^{ - \xi }}}}, $ | (6) |
其中,ω=k/(1-2k2α).若要求该解为实函数, 则应α>0,
类型3
| $ u\left( {x,t} \right) = \pm \sqrt k \sqrt p \sqrt \alpha \sqrt {\frac{{6k}}{{1 + {k^2}\alpha }}} \frac{2}{{{{\rm{e}}^\xi } + p{{\rm{e}}^{ - \xi }}}}, $ | (7) |
其中,ω=k/(1+k2α).若要求该解为实函数, 则应(i) α, p < 0,k2 > -1/α.此时波的相速度υp=1/(1+k2α) < 0,表明该波向左传播; 或(ⅱ)α>0, p < 0;或(ⅲ)α < 0, p>0,k2 < -1/α.对情形(ⅱ)和(ⅲ), 波的相速度υp=1/(1+k2α)>0,表明波向右传播.仅对情形(ⅲ), 该解为mBBM方程的钟型孤立波解, 无奇性; 对情形(i)和(ⅱ), 该解为奇异行波解.
类型4
| $ u\left( {x,t} \right) = \pm \sqrt {\frac{{ - 3{k^2}{r^2}\alpha }}{{{r^2}\left( {{k^2}\alpha - 2} \right) + 2p\left( {1 + {k^2}\alpha } \right)}}} \left[ {1 - \frac{{2{r^2} - 2p}}{r}f\left( \xi \right)} \right], $ | (8) |
其中,ω=2k(p-r2)/[r2(k2α-2)+2p(1+k2α)].若要求该解为实函数, 则应α/[r2(k2α-2)+2p(1+k2α)] < 0.当r>0, p≥0或-p < r≤0时, 该解为mBBM方程的孤立波解, 无奇性; 否则该解为奇异行波解.仅当α < 0, p < -r2/2, k2>2(r2-p)/[α(r2+2p)],波的相速度υp=2(p-r2)/[r2(k2α-2)+2p(1+k2α)] < 0,表明该波向左传播, 此时为奇异行波解;否则υp>0,波向右传播.
此种孤立波的结构与参数r与p的取值有很强的依赖性. 图 1显示(8)式(取“-”号)表示的波形随p值的变化, 各参数分别取为α=6, r=2, k=0.5, x0=0, t=0.从图 1可以看出, 当p=0.3时, 为典型的钟型孤立波; 当p=10-4时, 波形出现明显的双扭结状结构; 随着p的进一步减小, 如当p=10-7时, 双扭结状波的宽度进一步加大; 当p=0时, 波形变为单扭结状.
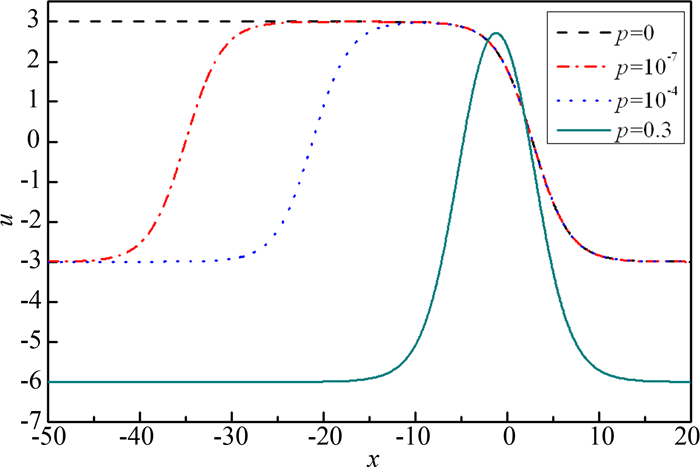 |
| 图 1 mBBM方程孤立波结构随参数p的变化(α=6, r=2, k=0.5, x0=0, t=0) Fig.1 Wave profiles of solitary wave at different p |
图 2显示具有双扭结状结构的孤立波u(x, t)及∂u/∂x在t=0时的波形.从图中可以看出, ∂u/∂x的波形具有反向双峰孤立子的结构特征.由于这里考虑的是行波, 故波在传播时, 波形及双峰之间的距离保持不变.定义∂u/∂x两波峰之间的距离为双扭结孤立波的波宽W,于是
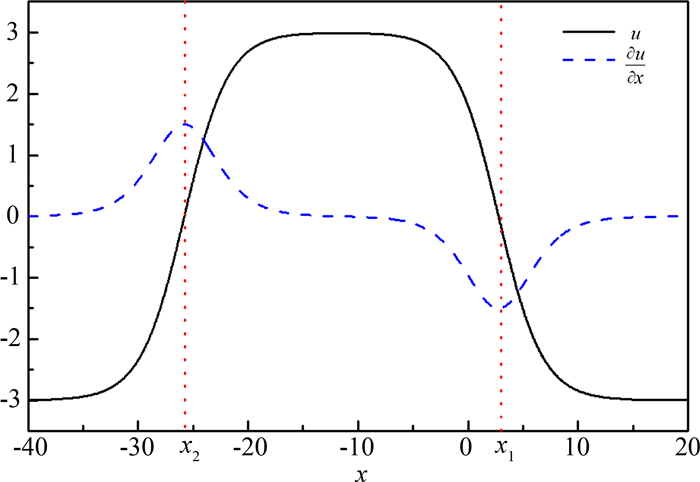 |
| 图 2 u(x, 0)和∂u(x, 0)/∂x的波形图(α=6, r=2, k=0.5, x0=0, t=0, p=10-5) Fig.2 Wave profiles of u(x, 0) and ∂u(x, 0)/∂x |
| $ W = \left| {{x_1}\left( t \right) - {x_2}\left( t \right)} \right| = \frac{1}{{\left| k \right|}}\left| {{\xi _1}\left( t \right) - {\xi _2}\left( t \right)} \right|, $ | (9) |
经简单计算得
| $ W = \frac{1}{{\left| k \right|}}\ln \left( {\frac{{1 + \sqrt {1 + 8\frac{p}{{{r^2}}}} + \sqrt 2 \sqrt {1 + 2\frac{p}{{{r^2}}} + \sqrt {1 + 8\frac{p}{{{r^2}}}} } }}{{1 + \sqrt {1 + 8\frac{p}{{{r^2}}}} - \sqrt 2 \sqrt {1 + 2\frac{p}{{{r^2}}} + \sqrt {1 + 8\frac{p}{{{r^2}}}} } }}} \right). $ | (10) |
从(10)式可以看出, 波宽W与波数k成反比且仅与p/r2的值有关.分析结果表明:当0 < p/r2≪1时, 该孤子具有明显的双扭结状结构; 当p/r2≈1或p/r2>1时, 该孤子为典型的钟型孤立波. 图 3显示k=0.5时波宽随p/r2的变化.从图中可以看出, 当p/r2逐渐减小时, 波宽W逐渐增大.当p/r2趋近0时, 波宽W急剧增加.理论计算表明, 当p/r2→+∞时, W趋于定值
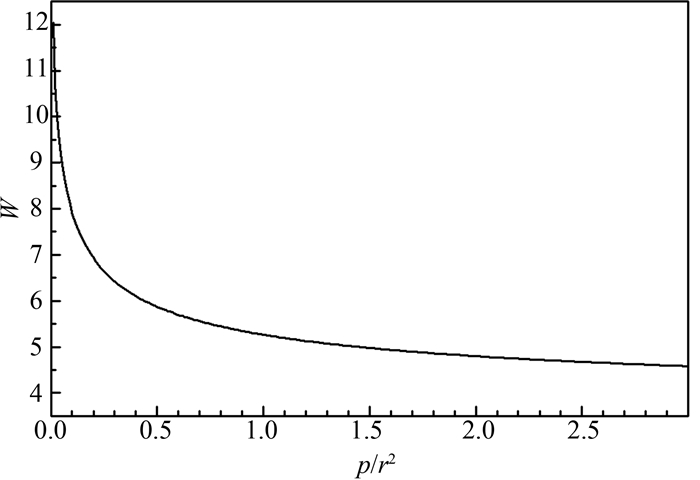 |
| 图 3 波宽W随p/r2的变化(k=0.5) Fig.3 Wave-width as a function of p/r2 |
振幅A可以定义为
| $ A = \mathop {\max }\limits_{ - \infty < x < + \infty } \left( {\left| {u\left( {x,t} \right)} \right| - u\left( {\infty ,t} \right)} \right). $ | (11) |
理论计算表明, 当x=1/(2k) lnp+ωt/k-x0/k时u取得极值
| $ u\left( {x,t} \right) = \mp \sqrt {\frac{{ - 3{k^2}\alpha }}{{\left( {{k^2}\alpha - 2} \right) + 2\left( {1 + {k^2}\alpha } \right)p/{r^2}}}} \left( {1 - 2\sqrt {p/{r^2}} } \right), $ | (12) |
且
| $ u\left( {\infty ,t} \right) = \pm \sqrt {\frac{{ - 3{k^2}\alpha }}{{\left( {{k^2}\alpha - 2} \right) + 2\left( {1 + {k^2}\alpha } \right)p/{r^2}}}} , $ | (13) |
从而得
| $ A = \sqrt {\frac{{-12{k^2}\alpha }}{{{k^2}\alpha-2 + 2\left( {1 + {k^2}\alpha } \right)p/{r^2}}}} \left| {1-\sqrt {\frac{p}{{{r^2}}}} } \right|. $ | (14) |
当p/r2接近于0时,
非线性波在传播时的动力学稳定性, 无论是理论上还是在实验上, 都是一个重要的问题.对于不稳定的波, 由于在实验中总存在不同程度的扰动, 故其无法长时间存在下去, 这样对于实验观测是很不利的.而稳定的波具有较强的抗干扰能力, 可以长时间存在, 故在实验中容易观测.下面采用数值方法研究mBBM方程孤立波的动力学稳定性.假设u0=u0(x, t)是mBBM方程的一精确解, 在t=0时刻对其加一个小的扰动u′(x, 0)=ε(x),记u(x, t)=[1+u′(x, t)]u0且设u(x, t)满足方程(1), 则可以通过考察u(x, t)随时间的演化而得知u0的动力学稳定性.一般说来, 若经过足够长时间的动力学演化后, 如果扰动的振幅没有产生明显的增加, 而且波形结构基本能够保持, 则可判定该波是动力学稳定的.若扰动的振幅产生明显的增加或波形结构发生明显改变, 则可判定该波是动力学不稳定的.
对mBBM方程(1), 建立如下有限差分格式对其孤立波进行动力学演化
| $ \begin{array}{*{20}{c}} {\frac{{u_j^{n + 1} - u_j^n}}{\tau } + \frac{{u_{j + 1}^{n + 1} - u_{j - 1}^{n + 1} + u_{j + 1}^n - u_{j - 1}^n}}{{4h}} + \frac{1}{9}{{\left( {u_{j + 1}^n + u_j^n + u_{j - 1}^n} \right)}^2}\frac{{u_{j + 1}^{n + 1} - u_{j - 1}^{n + 1} + u_{j + 1}^n - u_{j - 1}^n}}{{4h}} + }\\ {\alpha \frac{{u_{j + 1}^{n + 1} - u_{j - 1}^{n + 1} + u_{j + 1}^n - u_{j - 1}^n - 2u_j^{n + 1} + 2u_j^n}}{{{h^2}\tau }} = 0,} \end{array} $ | (15) |
其中τ和h分别为时间和空间方向步长, ujn表示u在(xj, tn)处的近似值.该格式为两层隐式格式, 其截断误差为
| $ \begin{array}{*{20}{c}} {T\left( {{x_j},{t_n}} \right) = \frac{\tau }{2}{{\left[ {\frac{{{\partial ^2}u}}{{\partial {t^2}}} + \left( {1 + {u^2}} \right)\frac{{{\partial ^2}u}}{{\partial {x^2}\partial {t^2}}}} \right]}_{\left( {{x_j},{t_n}} \right)}} + o\left( {{\tau ^2}} \right) + }\\ {\frac{{{h^2}}}{{12}}{{\left( {8u\frac{{\partial u}}{{\partial x}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2\frac{{{\partial ^3}u}}{{\partial {x^3}}} + 2{u^2}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \alpha \frac{{{\partial ^5}u}}{{\partial {x^4}\partial t}}} \right)}_{\left( {{x_j},{t_n}} \right)}} + o\left( {\tau {h^2} + {h^3}} \right) = o\left( {\tau + {h^2}} \right),} \end{array} $ | (16) |
故该格式对时间步长τ具有1阶精度, 对空间步长h则有2阶精度.对该格式进行线性稳定性分析[16], 设ujn=Vneijmh,得误差增长因子
| $ G = \frac{{18\left( {{h^2} - 2\alpha } \right) + 36\alpha \cos \left( {mh} \right) - {\rm{i}}h\left( {9 + {\sigma ^2}} \right)\tau \sin \left( {mh} \right)}}{{18\left( {{h^2} - 2\alpha } \right) + 36\alpha \cos \left( {mh} \right){\rm{ + i}}h\left( {9 + {\sigma ^2}} \right)\tau \sin \left( {mh} \right)}}, $ | (17) |
其中,
对格式(15), 当第n层的值已知而求第n+1层的值时, 其构成一线性代数方程组.实际计算是在一个有限区域上进行, 如果边界点的值已知, 则此代数方程组为三对角方程组, 可用追赶法求解.但一般情况下, 边界点的值未知, 则此时不宜采用追赶法求解.具体计算时, 我们选择计算区间x∈[-100, 100],步长τ=0.001, h=0.2,采用周期性边界条件.此时该代数方程组一般不构成三对角方程组, 可用高斯消元法进行求解.本文着重考察mBBM方程双扭结孤立波的稳定性, 故选择u0为(8)式(取“-”号), 其它参数取为r=2, k=0.5, x0=20.下面考察三种类型的初始扰动下孤立波的稳定性.
情况1:简谐波扰动.记初始扰动为
| $ \varepsilon \left( x \right) = A'\sin \left( {\frac{{2{\rm{\pi }}}}{\lambda }x} \right), $ | (18) |
其中A′, λ分别是扰动波的振幅和波长. 图 4显示当λ=20, A′=0.05时u(x, t)在不同时刻的波形图.可以看出, 随着时间的增加, 扰动波的振幅始终在很小, 没有明显的增加, 而且孤立波的波形结构也没发生明显改变.表明在长波扰动下, 该双扭结型孤立波是动力学稳定的. 图 5显示了当λ=2, A′=0.05时u(x, t)在不同时刻的波形图, 也可看出, 此时的双扭结孤立波在短波扰动下也是稳定的.数值模拟过程中, 我们考察了不同波长情况下的简谐波扰动, 但均没发现不稳定现象.在合理范围内改变参数k, p, r,也没观察到不稳定现象.该结果表明, mBBM方程描述的孤立波, 对于简谐波扰动, 具有很强的抗干扰性, 是动力学稳定的.
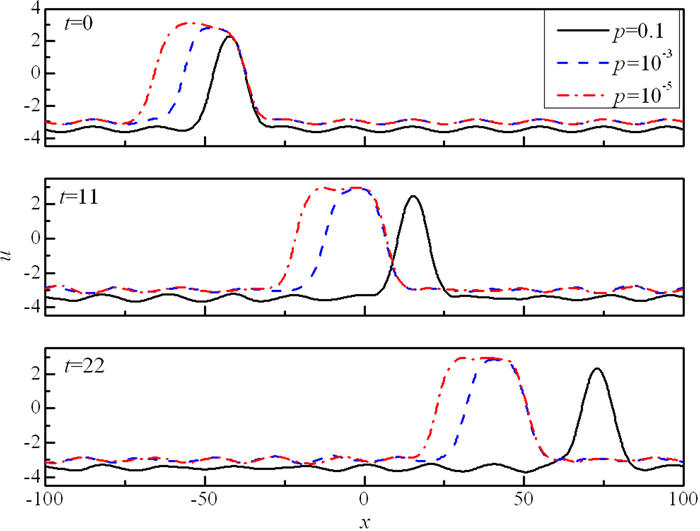 |
| 图 4 长波扰动下双扭结孤立波在不同时刻的波形图(λ=20, A′=0.05) Fig.4 Wave profiles of a solitary wave under long-wavelength disturbance at different time |
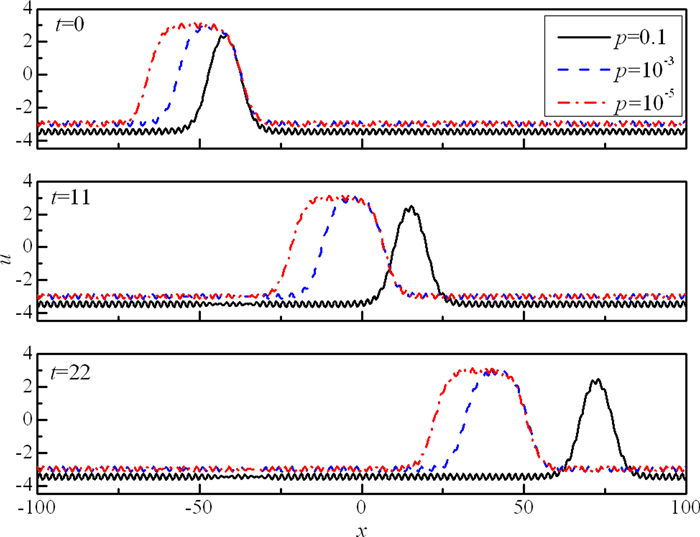 |
| 图 5 短波扰动下双扭结孤立波在不同时刻的波形图(λ=2, A′=0.05) Fig.5 Wave profiles of a solitary wave under short-wavelength disturbance at different time |
情况2:钟型波扰动.记初始扰动为
| $ \varepsilon \left( x \right) = A'{\mathop{\rm se}\nolimits} {\rm{ch}}\left( x \right), $ | (19) |
该扰动具有局域性, 其中A′表示初始扰动的振幅. 图 6显示了当A′=0.1时, 不同时刻的波形图.从图中可以看出, 随着时间的增加, 初始时刻局部的钟型扰动, 逐渐扩散为整个计算区间上的扰动, 但扰动的振幅并没发生明显增加.经长时间演化后, 孤立波的结构特征仍保持完好, 说明mBBM方程的双扭结孤立波在钟型波扰动下依然稳定.
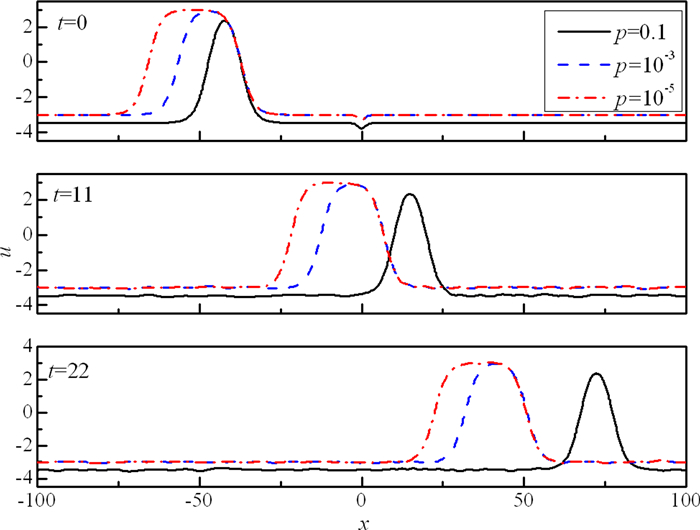 |
| 图 6 钟型波扰动下双扭结孤立波在不同时刻的波形图(A′=0.1) Fig.6 Wave profiles of a solitary wave under bell-like wave disturbance at different time |
这一点也可做如下理解:钟型波扰动可看做是很多简谐波扰动的叠加.由于在简谐波扰动时, 不存在不稳定波模, 故在钟型波扰动下, 该孤立波自然也是动力学稳定的.
情况3:随机扰动.设初始时刻各节点上的扰动为一随机数, 随机数区间取为[-0.005, 0.005].图 7显示了此时孤立波随时间的演化.从中可以看出, 扰动波的振幅始终保持很小, 而且孤立波结构也始终保持, 故此时的双扭结孤立波仍然稳定.该结果也可与前面做类似理解:随机扰动也可看做是很多简谐波扰动的叠加.由于不存在不稳定波模, 故在随机扰动下, 双扭结孤立波也是动力学稳定的.
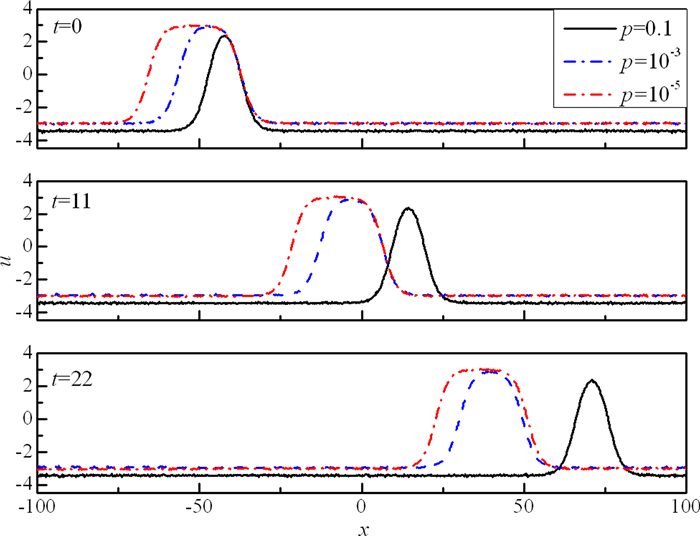 |
| 图 7 随机扰动下双扭结孤立波在不同时刻的波形图 Fig.7 Wave profiles of the solitary wave under random disturbance at different time |
前面的数值结果表明, mBBM方程的第4类孤立波是动力学稳定的.同样方法表明第3类孤立波也是动力学稳定的.下面对mBBM两孤立波的碰撞进行数值模拟研究, 数值格式仍采用有限差分格式(15).对(7)、(8)式表达的mBBM方程的非奇异孤立波, 其相速度υp>0,即波均向右传播.设初始时刻u(x, 0)=u(1)(x, 0)+u(2)(x, 0),其中u(i)(x, t)(i=1, 2)分别为由(7)式或(8)式表达的mBBM方程的孤立波解.初始时刻两孤立波波峰相距足够远, 且至少有一个孤立波具有局域性, 即u(1)(±∞, t)=0或u(2)(±∞, t)=0.通过数值研究u(x, t)随时间的演化便可模拟两孤立波的碰撞过程.数值模拟时, 我们取计算区间x∈[-100, 100],步长τ=0.001, h=0.2,采用周期性边界条件.不失一般性, 后面均取α=-1.
情况1完全弹性碰撞
取u(i)(x, t)(i=1, 2)为(7)式(取“-”号)表达的第3类孤立波, 此时u(i)(±∞, t)=0(i=1, 2).对应取两组不同参数k(1)=0.6, k(2)=0.4, p(1)=p(2)=1, x0(1)=36, x0(2)=0.两波若无相互作用, 其相速度分别为υp(1)=1.562 5,υp(2)=25/21≈1.190 5,有υp(1) > υp(2); 振幅分别约为1.837 12和1.069 05.初始时刻, 孤立波1位于孤立波2的左边. 图 8为双孤波碰撞过程的等值线图, 为使碰撞过程显示得更为清楚, 作图时只取了部分范围内数据.随着时间的增加, 第一个孤立波逐渐追上第二个孤立波并发生碰撞, 然后超过第二个孤立波, 直到两者再次分离, 并都恢复为初始时刻的波形.我们注意到, 在误差范围内, 碰撞后两孤波的振幅与速度均恢复为碰撞前的振幅与速度, 但位相产生明显变化.这一点与KdV方程描述的双孤子的碰撞极为类似.这种情况下的碰撞可看作是完全弹性碰撞.
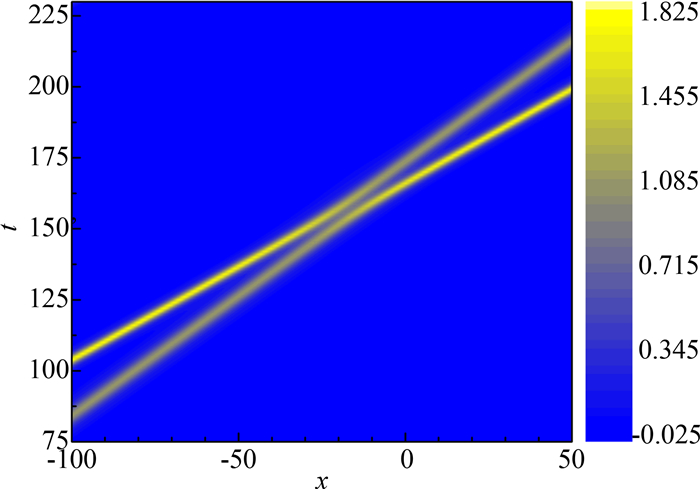 |
| 图 8 双孤波的完全弹性碰撞等值线图(k(1)=0.6, k(2)=0.4, p(1)=p(2)=1, x0(1)=36, x0(2)=0) Fig.8 Contour plot of a perfect elastic collision of two solitary waves |
情况2非完全弹性碰撞
取u(1)(x, t)为(7)式表达的孤立波(取“-”号), 其具有局域性, 即u(1)(±∞, t)=0; u(2)(x, t)为(8)式表达的孤立波(取“+”号), 有u(2)(±∞, t)≠0,即孤立波2是非局域性的; 其它参数分别取为k(1)=k(2)=0.5, p(1)=1, p(2)=5, r(2)=1.若两孤波之间不存在相互作用, 则孤波1的相速度υp(1)=4/3≈1.333 33,孤波2的相速度υp(2)=32/21≈1.523 81,有υp(1) > υp(2).但在数值模拟时发现, 由于孤立波2的非局域性, 两孤立波之间始终存在非线性相互作用, 孤立波1的速度实际大于孤立波2的速度, 分别为υp(1)′≈1.88,υp(2)′≈1.52,表明在这种非局域的相互作用下, 孤立波1的速度明显加快而孤立波2的速度基本不变. 图 9为此时两孤立波碰撞时的等值线图, 数值模拟时取x0(1)=40, x0(2)=20,即初始时刻孤立波1在孤立波2波峰的左边.随着时间的增加, 孤立波1逐渐追上孤立波2的波峰并发生碰撞, 但在此过程中产生了振幅和速度都很小的尾波.碰撞结束后, 两波的速度和振幅都近似地恢复到碰撞前.此情况下, 两孤立波之间的碰撞可看作非完全弹性碰撞.
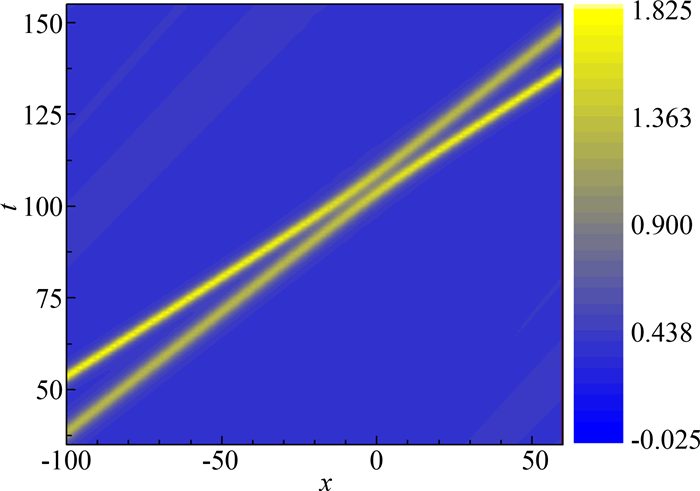 |
| 图 9 双孤波的非完全碰撞等值线图(k(1)=k(2)=0.5, p(1)=1, p(2)=5, r(2)=1,x0(1)=40, x0(2)=20) Fig.9 Contour plot of an non-perfect elastic collision of two solitary waves |
情况3完全非弹性碰撞.
取u(1)(x, t)为(7)式表达的孤立波(取“+”号), 其具有局域性, 即u(1)(±∞, t)=0; u(2)(x, t)为(8)式表达的孤立波(取“+”号), 有u(2)(±∞, t)≠0,即孤立波2是非局域性的; 其它参数分别取为k(1)=k(2)=0.5, p(1)=1, p(2)=5, r(2)=1(同情况2).若两孤波之间不存在相互作用, 则孤波1的相速度υp(1)≈1.333 33,孤波2的相速度υp(2)≈1.523 81,有υp(1) < υp(2).与情况2不同的是:尽管孤立波2具有非局域性, 两孤立波之间始终存在非线性相互作用, 但碰撞前孤立波1的速度仍小于孤立波2的速度, 分别为υp(1)′≈0.933 33,υp(2)′≈1.533 33. 图 10为此时两孤立波碰撞时的等值线图, 数值模拟时取x0(1)=20, x0(2)=40,即初始时刻孤立波2的波峰在孤立波1的左边.随着时间的增加, 孤立波2的波峰逐渐追上孤立波1并发生碰撞.在此过程中, 不断有尾波产生, 并且尾波的振幅相比情况2要大得多.数值模拟结果表明, 如果在计算时空间范围足够大, 则经长时间演化后, 原始的两孤立波的波形被破坏殆尽, 最终形成传播速度较快的孤立波在前(右边), 而速度较慢的波在后(左边)的孤立波序列.这种情况可看作是完全非弹性碰撞.
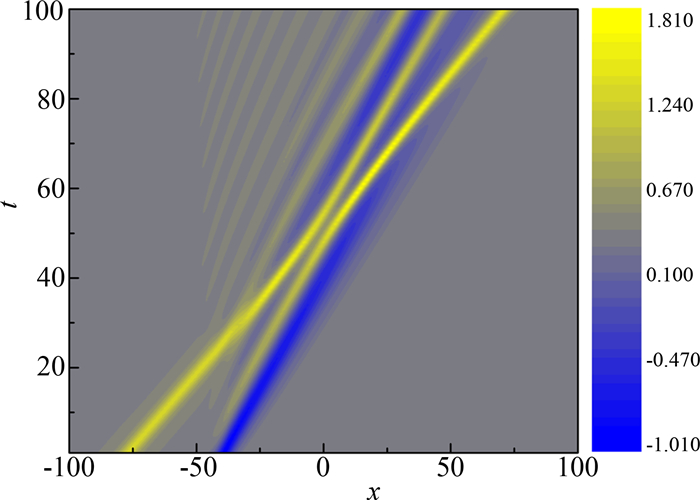 |
| 图 10 双孤波的完全非弹性碰撞等值线图(k(1)=k(2)=0.5, p(1)=1, p(2)=5, r(2)=1,x0(1)=20, x0(2)=40) Fig.10 Contour plot of a completely inelastic collision of two solitary waves |
采用扩展双曲函数展开法, 得到mBBM方程4类精确行波解, 其中一类具有扭结-反扭结状结构.在不同极限情况下, 该孤子分别退化为mBBM方程的扭结型或钟型孤立波解.对该类孤子的结构特征进行理论分析, 并构造有限差分格式对该类孤子的动力学稳定性进行数值研究.有限差分格式为两层隐式格式, 在线性化意义下绝对稳定.数值结果表明, mBBM方程的双扭结型孤立波解, 在不同类型的扰动下, 具有很强的稳定性.对双孤立波的碰撞过程进行数值模拟, 发现既存在弹性碰撞, 也存在非弹性碰撞.对于其它非线性演化方程, 是否存在双扭结状孤立波解, 以及孤立波是否稳定, 是值得研究的问题.
| [1] | BENJAMIN T B, BONA J L, MAHONY J J. Model equation for long waves in nonlinear dispersive systems[J]. Philos Trans Roy Soc London Ser , 1972, 272A :47–78. |
| [2] | MOLATI M, KHALIQUE C M. Symmetry classification and invariant solution of the variable coefficient BBM equation[J]. Applied Mathematics and Computation , 2013, 219 :7917–7922. doi:10.1016/j.amc.2013.02.036 |
| [3] | SHANG Yadong, NIU Pengcheng. Exact solitary wave solutions of several nonlinear evolution equations[J]. Pure and Applied Mathematics , 1998, 14 (1) :74–79. |
| [4] | YAN Fang, LIU Haihong, LIU Zengrong. The bifurcation and exact travelling wave solutions for modified Benjamin-Bana-Mahoney (mBBM) equation[J]. Commun Nonlinear Sci Numer Simulat , 2012, 17 :2824–2832. doi:10.1016/j.cnsns.2011.11.014 |
| [5] | YANG Kunwang. Applying EXP-function method for solving nonlinear evolution equations[J]. Pure and Applied Mathematics , 2012, 28 (1) :85–91. |
| [6] | LI Xiangzheng, WANG Mingliang, LI Xiaoyan. Applications of F-expansion to periodic wave solutions for KdV equation[J]. Mathematica Applicata , 2005, 18 (2) :303–307. |
| [7] | LIANG Liwei, LI Xingdong, LI Yuxia. The extended F-expansion method and new exact solutions of the generalized KdV equation[J]. Acta Physica Sinica , 2009, 58 (4) :2159–2163. |
| [8] | ZHANG Jinliang, WANG Mingling, WANG Yueming. The extended F-expansion method and the exact solutions to the KdV and mKdV equation with variable coefficients[J]. Acta Mathematica scientia , 2006, 26A (3) :353–360. |
| [9] | ZHANG Guxu, LI Zhibin, DUAN Yishi. Exact solitary wave solution of nonlinear wave equations[J]. Science in China Ser A , 2001, 44 (3) :396–401. doi:10.1007/BF02878721 |
| [10] | SHI Yuren, ZHANG Juan, YANG Hongjuan, DUAN Wenshan. Single soliton of double kinks of the mKdV equation and its stability[J]. Acta Physica Sinica , 2010, 59 (11) :7564–7569. |
| [11] | SHI Yuren, ZHOU Zhigang, ZHANG Juan, YANG Hongjuan, DUAN Wenshan. Solitary wave solutions of modified coupled KdV equation and their stability[J]. Chinese Journal of Computational Physics , 2012, 29 (2) :250–256. |
| [12] | SHI Yuren, ZHANG Juan, YANG Hongjuan, DUAN Wenshan. The single solitary wave with double peaks of the coupled KdV equation and its stability[J]. Acta Physica Sinica , 2011, 60 (2) :020401–1. |
| [13] | LAYENI O P, AKINOLA A P. A new hyperbolic auxiliary function method and exact solutions of the mBBM equation[J]. Commun Nonlinear Sci Numer Simulat , 2010, 15 (2010) :135–138. |
| [14] | CHEN Songlin, HOU Weigen. Explicit exact solutions of generalized B-BBM and B-BBM equations[J]. Acta Physica Sinica , 2001, 50 (10) :1842–1845. |
| [15] | TAOGETUSANG, SIRENDAOERJI. New exact solitary wave solutions to the BBM and mBBM equations[J]. Acta Physica Sinica , 2004, 53 (12) :4052–4060. |
| [16] | LU Jinfu, GUAN Zhi. Numerical methods for solving partial differential equations[M]. Beijing: Tsinghua University Press , 2003 : 28 -39. |
 2016, Vol. 33
2016, Vol. 33


