| 特低渗透油藏面积井网见水时间计算 |
2. 中国石油大学(北京), 北京 102249
2. China University of Petroleum-Beijing, Beijing 102249, China
目前,越来越多的特低渗透油藏已投入开发,且普遍采用注水开发技术.当注水井注水后,注入水沿最速流线到达采油井的时间为见水时间.油井的见水时间对油井生产管理影响重大,因此,能准确预测油井的见水时间至关重要.文献[1]根据油水两相渗流的Beckley-Leverett方程推导了定产条件下的油井见水时间公式.文献[2-4]运用等值渗流阻力方法,考虑水驱油的非活塞特性,推导了水平井与直井联合井网的油井见水时间公式.文献[5]基于渗流力学理论,推导了均质油藏反九点井网油井见水时间公式,并针对人工裂缝对公式进行了修正.特低渗透油藏的渗流特征与中、高渗储层存在明显差异,表现为非达西渗流[6-12],且由于地质沉积和微裂缝发育等因素的影响,特低渗透油藏往往表现出渗透率各向异性[13-17],因此,以上文献所给出的见水时间公式不适用于特低渗透油藏.文献[18-20]基于流管模型,推导了考虑启动压力梯度的四点井网、五点井网、反九点井网和菱形反九点井网的油井见水时间公式,但是公式并未考虑油水黏度差异以及渗透率各向异性等因素.因此,本文针对特低渗透油藏的特征,考虑启动压力梯度、渗透率各向异性以及油水黏度的差异,推导了特低渗透油藏常用面积井网(五点、反九点和菱形反九点井网)油水两相非活塞式驱替的油井见水时间公式,以指导特低渗透油藏开发.
1 一源一汇见水时间在一源一汇渗流场中(图 1),A为注水井,B为生产井,井间距离为L.根据渗流理论可知在主流线上的渗流速度最快,因此,当注入水沿着主流线向生产井突破时,油井开始见水.见水时间计算模型的假设条件包括:
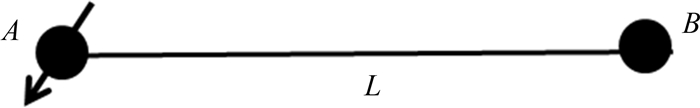 |
| 图 1 一注一采模型示意图 Fig.1 Schematic of injection-production model |
1) 流体为油水两相,且为非活塞式水驱油;
2) 不考虑多孔介质及流体的压缩性;
3) 地层均质等厚;
4) 不考虑毛管力和重力的作用;
5) 渗流过程是等温的;
6) 渗流方程考虑启动压力梯度.
在主流线AB上油水两相渗流的渗流速度[7]为
| $ v=\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda L \right)/\left[\frac{{{\mu }_{\text{o}}}}{k}\int\limits_{0}^{{{x}_{\text{f}}}}{\frac{\text{d}x}{{{\mu }_{\text{r}}}{{k}_{\text{rw}}}+{{k}_{\text{ro}}}}}+\frac{{{\mu }_{\text{o}}}\left( L-{{x}_{\text{f}}} \right)}{k} \right], $ | (1) |
式中,v为渗流速度,m·s-1;pi为注入井井底压力,MPa;pw为生产井井底压力,MPa;λ为启动压力梯度,MPa·m-1;L为流线长度,m;k为地层绝对渗透率, 10-3μm2; μ0为地层原油黏度,MPa·s;μr为油水黏度比,无因次;kro为油相相对渗透率,无因次;krw为水相相对渗透率,无因次;xf为流线中水驱前缘位置,m;
| $ \frac{{{\mu }_{\text{o}}}}{k}\int\limits_{0}^{{{x}_{\text{f}}}}{\frac{\text{d}x}{{{\mu }_{\text{r}}}{{k}_{\text{rw}}}+{{k}_{\text{ro}}}}}=\frac{{{\mu }_{\text{w}}}}{k}\int\limits_{0}^{{{x}_{\text{f}}}}{\frac{{{f}_{\text{w}}}\left( {{s}_{\text{w}}} \right)\text{d}x}{{{k}_{\text{ro}}}}}=\frac{{{\mu }_{\text{w}}}}{k}\frac{{{x}_{\text{f}}}}{f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)}\int\limits_{0}^{f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)}{\frac{{{f}_{\text{w}}}\left( {{s}_{\text{w}}} \right)}{{{k}_{\text{rw}}}}}\text{d}f{{'}_{\text{w}}}\left( {{s}_{\text{w}}} \right). $ | (2) |
式中,fw(sw)为含水率,无因次;f′w(swf)为前缘含水饱和度所对应的含水变化率,无因次.若令
| $ \frac{{{\mu }_{\text{o}}}}{k}\int\limits_{0}^{{{x}_{\text{f}}}}{\frac{\text{d}x}{{{\mu }_{\text{r}}}{{k}_{\text{rw}}}+{{k}_{\text{ro}}}}}=\frac{{{\mu }_{\text{w}}}{{x}_{\text{f}}}}{k}\alpha . $ | (3) |
当注采压差保持不变时,水驱前缘位置满足[8]
| $ {{x}_{\text{f}}}=\frac{f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)}{\phi }\int\limits_{0}^{t}{v}\text{d}t. $ | (4) |
式中,ϕ为孔隙度,无因次;t为时间,d.联立式(1)和式(4)可得
| $ {{x}_{\text{f}}}=\frac{f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)}{\phi }\int\limits_{0}^{t}{\frac{{{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda L}{\lambda {{'}_{\text{w}}}{{x}_{\text{f}}}+\lambda {{'}_{\text{o}}}\left( L-{{x}_{\text{f}}} \right)}}\text{d}t, $ | (5) |
式中,λ′w=μwα/k,λ′o=μo/k.
对式(5)先求导后积分可得
| $ \frac{\left( \lambda {{'}_{\text{w}}}-\lambda {{'}_{\text{o}}} \right)}{2}x_{\text{f}}^{2}+\lambda {{'}_{\text{o}}}L{{x}_{\text{f}}}-\frac{f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda L \right)t}{\phi }=0. $ | (6) |
当xf=L时油井见水,见水时间
| $ T=\frac{\phi \left( \lambda {{'}_{\text{w}}}+\lambda {{'}_{\text{o}}} \right){{L}^{2}}}{2f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda L \right)}. $ | (7) |
由以上分析可知五点井网(图 2)油水前缘到达生产井底的时间为
| $ T=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right){{d}^{2}}}{2kf{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda d \right)}. $ | (8) |
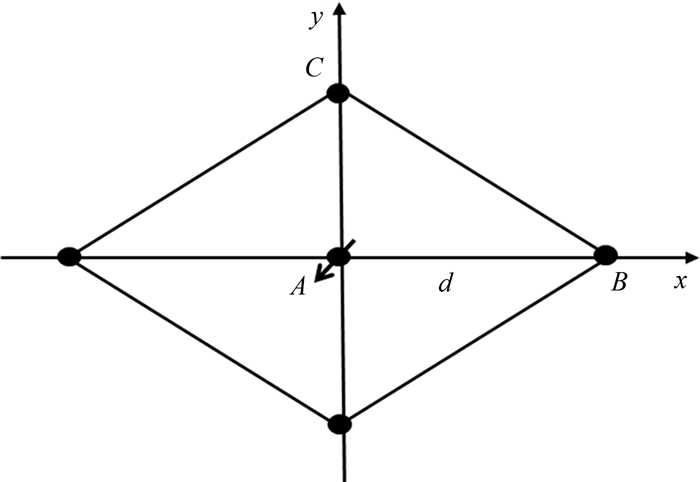 |
| 图 2 五点井网示意图 Fig.2 Schematic of 5-spot well pattern |
由于特低渗透油藏往往受沉积等地质因素的控制,储集层渗透率常表现出各向异性的特征.假设五点井网井排方向和渗透率主值方向平行或垂直,可通过坐标转化将原来渗流空间里以kx和ky为渗透率主值且各向异性强度为β(
主流线AB上注入水的突破时间为
| $ {{T}_{1}}=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right){{d}^{2}}/\beta }{2{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda d/\sqrt{\beta } \right)} $ | (9) |
主流线AC上注入水的突破时间为
| $ {{T}_{2}}=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right)\beta {{d}^{2}}}{2{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda \sqrt{\beta }d \right)}. $ | (10) |
因此,当考虑渗透率各向异性时,五点井网的见水时间为
| $ T=\min \left( {{T}_{1}}, {{T}_{2}} \right). $ | (11) |
反九点井网(图 3)的边井和角井具有不同的几何特征,因此需要分别考虑.边井与五点井网相似,可通过公式(11)求得反九点井网边井见水时间.角井的见水时间为
| $ T=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right)\left( \left( 1+{{\beta }^{2}} \right)/\beta \right){{d}^{2}}}{2{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda \sqrt{\left( 1+{{\beta }^{2}} \right)/\beta }d \right)}. $ | (12) |
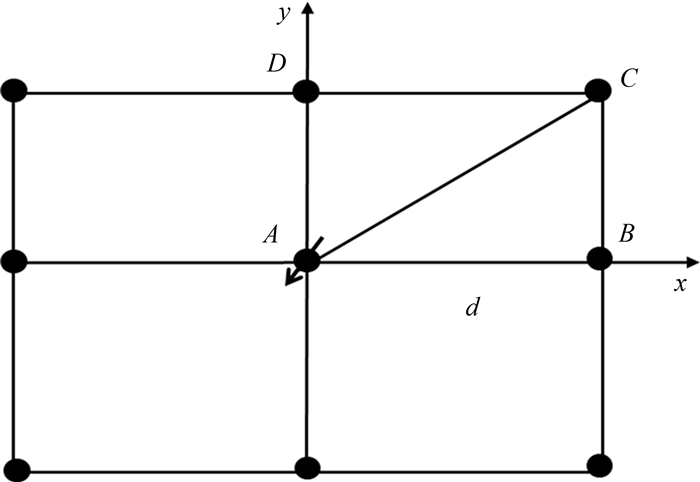 |
| 图 3 反九点井网示意图 Fig.3 Schematic of inverted 9-spot well pattern |
菱形反九点井网是特低渗透油藏注水开发常用井网(图 4),长轴方向井距为d1,短轴方向井距为d2,长轴方向(主流线AB)上注入水的突破时间为
| $ {{T}_{3}}=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right)d_{1}^{2}/\beta }{2{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda {{d}_{1}}/\sqrt{\beta } \right)}. $ | (13) |
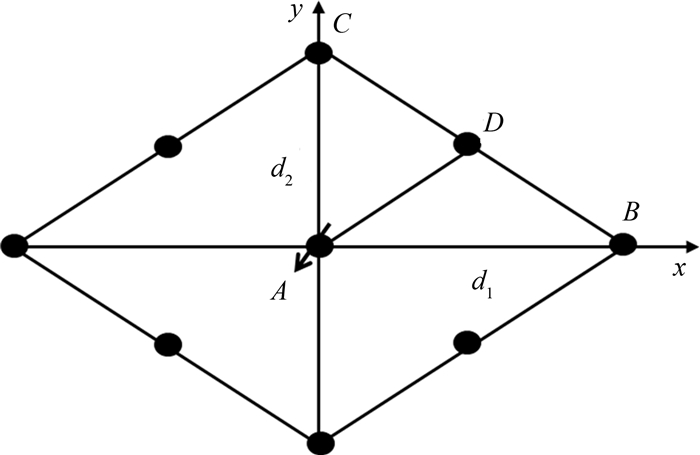 |
| 图 4 菱形反九点井网示意图 Fig.4 Schematic of diamond shaped inverted 9-spot well pattern |
短轴方向(主流线AC)上注入水的突破时间为
| $ {{T}_{4}}=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right)\beta d_{2}^{2}}{2{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda \sqrt{\beta }{{d}_{2}} \right)}. $ | (14) |
因此,菱形反九点井网角井的见水时间为
| $ T=\min \left( {{T}_{3}}, {{T}_{4}} \right). $ | (15) |
菱形反九点井网边井的见水时间为
| $ \begin{align} &T=\frac{\phi \left( {{\mu }_{\text{w}}}\alpha +{{\mu }_{\text{o}}} \right)\left( d_{1}^{2}/\beta d_{2}^{2} \right)}{8{{k}_{\text{eq}}}f{{'}_{\text{w}}}\left( {{s}_{\text{wf}}} \right)\left( {{p}_{\text{i}}}-{{p}_{\text{w}}}-\lambda \sqrt{d_{1}^{2}/\beta +\beta d_{2}^{2}/2} \right)}. \\ & \\ \end{align} $ | (16) |
以长庆鄂尔多斯盆地某一典型特低渗透油藏为例,分析油水黏度比、渗透率各向异性和启动压力梯度对特低渗透油藏见水时间的影响.油藏参数为:有效渗透率(k)为2×10-3 μm2,孔隙度为0.15,地层原油黏度为5 mPa·s,注入水的黏度为1.0 mPa·s,启动压力梯度为0.04 MPa·m-1,以油田的实际相渗曲线计算得到水驱前缘含水饱和度对应的含水变化率f′w(swf)=7.37,α=1.98.
3.1 油水黏度比针对五点井网,在井距为150 m、注采压差为30 MPa和启动压力梯度为0.04 MPa·m-1的情况下,研究油水黏度比对见水时间的影响.由表 1可知:对于相对渗透率曲线一定的油层,油井的见水时间取决于油水黏度比,且油水黏度比对见水时间的影响较大.当驱替液(水)黏度较小时,驱替液(水)的流动能力大于油的流动能力,驱替液(水)绕过油向前流动,从而使生产井过早见水;当驱替液(水)黏度较大时,驱替液(水)的流动能力变小,驱替趋向于活塞式,生产井见水越晚.因此,对于原油黏度较大的油藏,可通过运用化学试剂稠化注入水的方法来降低油井的见水时间.
| 表 1 油水黏度比对见水时间的影响 Table 1 Effects of viscosity ratio of oil and water on water breakthrough time |
 |
| 点击放大 |
由于受沉积等地质因素的影响,特低渗透油藏往往表现为渗透率各向异性,为了实现均衡驱替,长庆鄂尔多斯盆地常采用菱形反九点井网进行开发.菱形反九点井网的长轴方向井距和短轴方向井距之比为x(即图 4中d1/d2),在地层原油黏度为5 mPa·s、注入水的黏度为1.0 mPa·s、注采压差为30 MPa和启动压力梯度为0.04 MPa·m-1的情况下,研究渗透率各向异性对见水时间的影响.
从图 5可以看出:随着渗透率各向异性强度β的增大,短轴方向上的角井见水越晚,而长轴方向上的角井见水越早;当长轴方向井距与短轴方向井距之比x与渗透率各向异性强度β大致相等时,长轴方向角井与短轴方向角井同时见水.图 6为角井与注水井间压差保持为30 MPa,改变边井工作制度,在不同的边井与注水井间压差条件下,短轴方向上的角井和边井实现均衡驱替时x与β需满足的关系.从图 6可以看出:当边角井具有相同的工作制度时,即边角井注采压差相同,为实现短轴方向角井与边井同时见水,长轴方向井距与短轴方向井距之比x需大于渗透率各向异性强度β.因此,对于菱形反九点井网,在边角井具有相同的注采压差时,要实现边角井完全均衡驱替是不可能的,当长轴方向上的角井与短轴方向上的角井同时见水时,边井总是比角井先见水,此时可以通过适当减小边井与注水井间压差以达到边角井相对较高的均衡驱替.
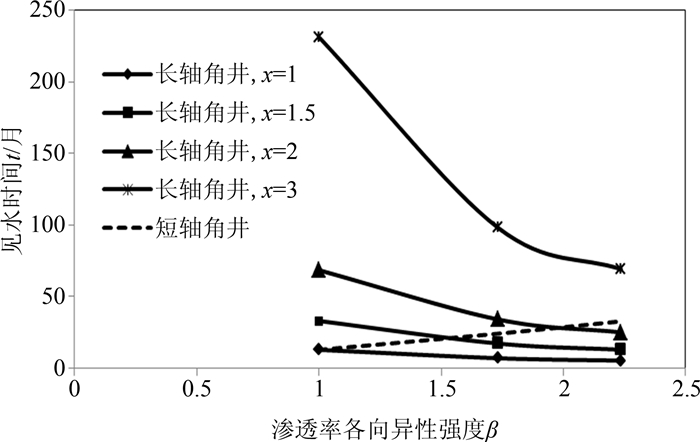 |
| 图 5 不同β与x条件下短轴方向角井及长轴方向角井的见水时间 Fig.5 Water breakthrough time of corner well under different β and x |
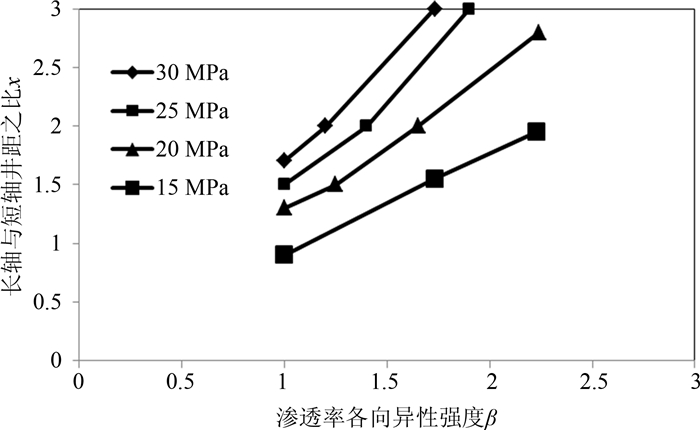 |
| 图 6 边井与短轴方向角井实现均衡驱替时β与x的关系 Fig.6 Relation between β and xas corner well and edge well are uniform displacement |
基于五点井网,在地层原油黏度为5 mPa·s、注入水的黏度为1.0 mPa·s、井距为150 m和注采压差为30 MPa的情况下,研究启动压力梯度对见水时间的影响.从图 7可以看出:随着启动压力梯度的增加,油井的见水越晚;当井距较小时,启动压力梯度对见水时间的影响较小,当井距较大时,启动压力梯度对见水时间的影响变得明显.这是因为由于启动压力梯度的存在,一部分生产压差需用于克服由启动压力梯度产生的额外阻力,造成有效生产压差减小,从而使得油井见水越晚,且当井距越大时,由启动压力梯度产生的额外阻力就越大,使得有效生产压差越小,油井的见水时间就越晚.
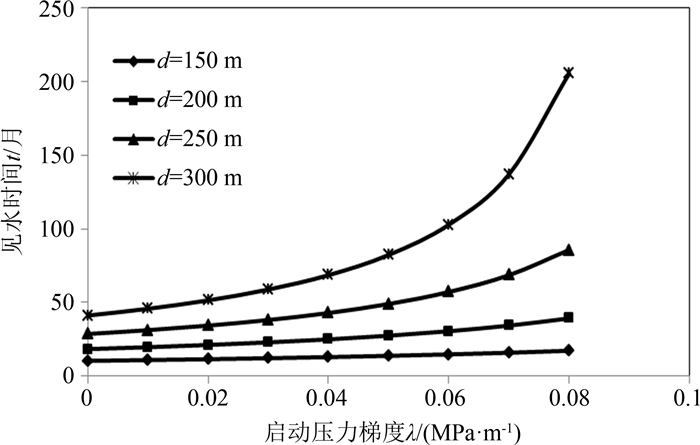 |
| 图 7 启动压力梯度对见水时间的影响 Fig.7 Effects of threshold pressure gradient on water breakthrough time |
鄂尔多斯盆地X油田属于特低渗透油藏,有效渗透率(k)为1.8×10-3 μm2,孔隙度为0.125,由于地质沉积和微裂缝发育的影响,X油田渗透率表现为各向异性,且各向异性强度为1.73.目前该区块采用菱形反九点井网开发,井排方向与渗透率主值方向平行(图 8),长轴方向井距(x方向)为480 m,短轴方向井距(y方向)为300 m,注采压差为30 MPa,地层原油黏度为2.0 mPa·s,注入水的黏度为0.4 mPa·s,启动压力梯度为0.03 MPa·m-1,以油田的实际相渗曲线计算得到水驱前缘含水饱和度对应的含水变化率f′w(swf)为7.37,α=1.98.
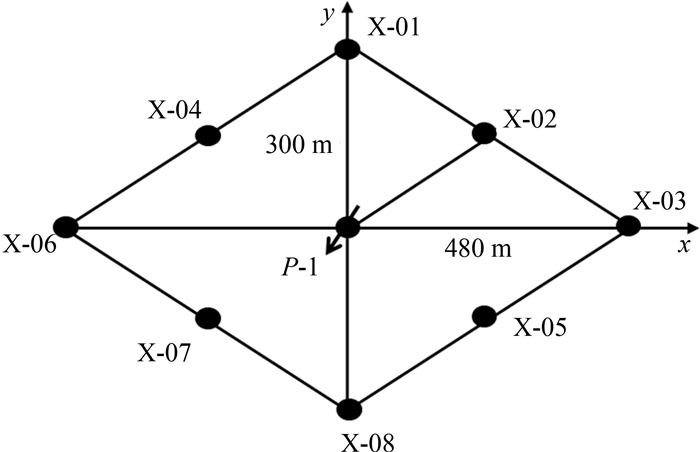 |
| 图 8 X油田P-1注采井组示意图 Fig.8 Schematic of P-1 well group in X oilfield |
根据该区块P-1注采井组实际含水率变化曲线(图 9)可以得到X-01井、X-02井和X-03井的见水时间分别为43个月、16个月和35个月.通过本文公式计算得到该区块P-1注采井组边角井的见水时间如表 2所示.对比本文公式计算结果和实际见水时间可知,理论计算值与实际值的计算误差在10%左右,基本符合油田含水率实际动态变化特征.同时,由于该区块所采用的菱形反九点井网的长轴方向井距与短轴方向井距之比等于1.6,与其渗透率各向异性强度相近,所以长轴方向与短轴方向见水时间相差不大,两个方向上的角井驱替均衡,但是边井的见水时间要早于角井.
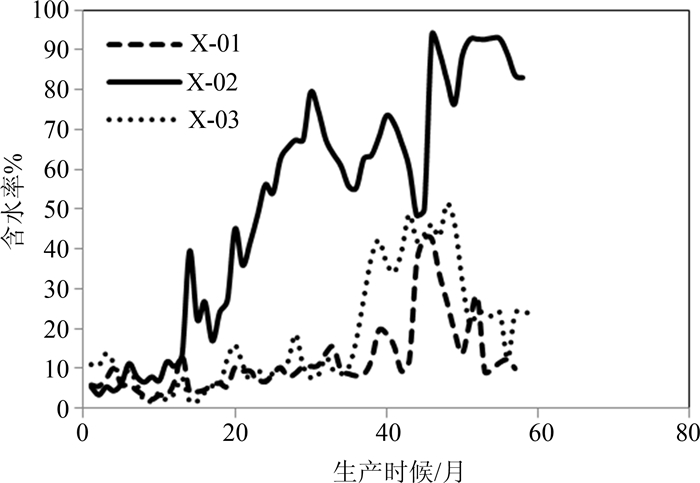 |
| 图 9 P-1井组含水率变化 Fig.9 Water cuts of P-1 well group |
| 表 2 P-1注采井组见水时间 Table 2 Water breakthrough time of P-1 well group |
 |
| 点击放大 |
1) 针对特低渗透油藏的渗透率各向异性和非达西渗流特征,推导了特低渗透油藏常用面积井网(五点、反九点和菱形反九点井网)油水两相非活塞式驱替的油井见水时间公式,并运用该公式对长庆鄂尔多斯盆地某特低渗透油藏实际井网进行见水时间计算,计算结果与实际动态符合性较好,能满足油藏工程的计算要求.
2) 油水黏度比越大,油井的见水时间越早;启动压力梯度的存在延缓了油井的见水时间,且生产井距越大,启动压力梯度的影响就越明显.
3) 当菱形反九点井网的长轴方向井距与短轴方向井距之比与渗透率各向异性强度大致相等时,长轴方向与短轴方向的角井能实现均衡驱替,要实现边井与角井的均衡驱替,则需通过调节油井的工作制度.
| [1] | JI Bingyu, ZHAN Jianfei, SU Zhixin. A theoretical calculation formula of responding and water breakthrough time of wells after water flooding[J]. Petroleum Geology & Oilfield Development in Daqing , 2000, 19 (5) :24–26. |
| [2] | WU Bingchang, YAO Jun, ZHANG Jihong, et al. Determination of water breakthrough time in horizontal-vertical well pattern[J]. Acta Petrolei Sinica , 2005, 26 (4) :111–114. |
| [3] | ZHAO Dongmei, WU Bingchang, YAO Jun, et al. Water breakthrough time in combination well pattern of horizontal and vertical well[J]. Journal of the University of Petroleum, China , 2005, 29 (5) :54–57. |
| [4] | YAO Kai, JIANG Hanqiao, WU Bingchang, et al. Water breakthrough time in combination well pattern of horizontal and vertical well[J]. Journal of Oil and Gas Technology , 2007, 29 (1) :114–117. |
| [5] | LI Peichao, DONG Hongmei, LI Yansheng, et al. Analytic formula for water breakthrough time of producers in inverted ninespot injection-production pattern[J]. Petroleum Geology & Oilfield Development in Daqing , 2009, 28 (1) :61–65. |
| [6] | HUANG Yanzhang. The mechanism of flow in low permeability reservoir[M]. Beijing: Petroleum Industry Press , 1998 : 58 -79. |
| [7] | GE Jiali. The modern mechanics of fluids flow in oil reservoir[M]. Beijing: Petroleum Industry Press , 2003 : 170 -199. |
| [8] | CHENG Linsong. Advanced fluid flow in porous media[M]. Beijing: Petroleum Industry Press , 2011 : 126 -142. |
| [9] | ONUR M, REYNOLDS A C. Nonlinear regression:The information content of pressure and pressure-derivative data[A]. SPE 79582, 2002:243-247. |
| [10] | XU Jianhong, CHENG Linsong, ZHOU Yin, et al. A new method for calculating kickoff pressure gradient in low permeability reservoirs[J]. Petroleum Exploration and Development , 2007, 3 (5) :594–597. |
| [11] | WU Yushu. Theoretical studies on non-Newtonian and Newtonian fluid flow through porous media[D]. University of California, Berkeley, 1990. |
| [12] | SHI Yu, YANG Zhengming, HUANG Yanzhang. Study on non-linear seepage flow model for low permeability reservoir[J]. Acta Petrolei Sinica , 2009, 30 (5) :731–734. |
| [13] | RAMEY H J. Interference analysis for anisotropic formations-a case history[J]. JPT , 1975, 27 (10) :25–29. |
| [14] | WALTER Rose. Permeability anisotropy in low permeability formations[J]. SPE 10810, 1982. |
| [15] | HIDAYATI D T, CHEN H Y. The reliability of permeability-anisotropy estimation from interference testing of naturally fractured reservoirs. SPE 59011, 2000. |
| [16] | CHEN H Y, TEUFEL L W. A quick method to determine permeability-anisotropy orientation from interference testing[J]. SPE 84090, 2003. |
| [17] | LIU Yuetian, XU Mingda, PENG Daogui, et al. Numerical simulation of petroleum reservoir with anisotropic permeability[J]. Chinses Journal of Computational Physics , 2007, 24 (3) :295–300. |
| [18] | GUO Fenzhuan, TANG Hai, LV Dongliang, et al. Calculation of water breakthrough time in non-Darcy seepage flow well pattern of low permeability reservoir[J]. Journal of Daqing Petroleum Institute , 2011, 35 (1) :42–45. |
| [19] | ZHU Shengju, WANG Ping, WANG Siyi, et al. Research on breakthrough time of diamond shaped inverted 9-spot pattern of low permeability reservoir[J]. Reservoir Evaluation and Development , 2013, 3 (2) :41–45. |
| [20] | GUO Fenzhuan, XI Tiande, MENG Xuangang, et al. Analysis of water breakthrough time of oil-well in low permeability reservoir[J]. Journal of Northeast Petroleum University , 2013, 37 (3) :87–93. |
 2016, Vol. 33
2016, Vol. 33

