| 多相非牛顿流体驱替过程的格子Boltzmann模拟 |
2. 北京大学工学院, 北京 100871
2. College of Engineering, Peking University, Beijing 100871, China
多相流体的驱替现象普遍存在于日常生活中,并且在微流体系统中得到广泛的应用,比如可以为芯片提供自身的逻辑控制[1-2],可以为生物化学实验提供良好的研究平台[3-7],并且在油气开采过程中十分普遍[8-10].这些应用往往涉及非常复杂的通道结构,并且流动特性复杂,存在很多的非牛顿流体,给研究带来了很大的困难.
对于复杂结构中的多相驱替问题,前人在理论以及数值模拟方面已经做了很多的工作[11-19],但绝大多数研究都是基于Darcy渗流理论并结合孔网模型[20]建立的,不仅结构被简化为由规则形状构建的网络,而且忽略了很多物理作用细节,并引入了很多经验参数,而正是这些细节,对于理解复杂结构中的驱替机理十分关键.
经过数十年的发展,格子Boltzmann方法(LBM)因其边界条件简单、易于处理复杂传递过程、易于并行等优点[21-24],已成为解决流动传热等问题的有效数值研究工具之一,能够从细节层面研究复杂结构中的多相驱替过程.在多相流方面,前人早期已经提出了多种LBM模型:Gunstensen等人提出的染色模型[25-26],Shan和Chen提出的拟势模型[27],Swift等人提出的自由能模型[28],以及He等人提出的平均场模型[29-30].但这些早期的模型有一个共同的缺陷,即难以处理大密度比的两相流动.为解决此问题,陆续发展了几种大密度比模型,如Inamuro等人提出的模型[31]和Zheng等人提出的模型[32].然而前者由于采用射影法将速度和压力解耦求解,过程繁琐,丧失了LBM的计算效率;相比于前者,后者则更为高效.
1 数值模拟方法 1.1 大密度比多相流LBM模型本文所采用的模型[33]是借鉴早期自由能模型[28]思想建立的,通过引入两个分布函数fi和gi,分别演化流体的质量和动量输运过程以及两相界面迁移过程.其离散化的LB方程为
| $ {f_i}\left( {{x} + {{c}_i}\Delta t,t + \Delta t} \right) - {f_i}\left( {{x},t} \right) = - \frac{1}{{{\tau _f}}}\left( {{f_i}\left( {{x},t} \right) - f_i^{{\rm{eq}}}\left( {{x},t} \right)} \right) + \frac{{3\Delta t{\omega _i}{{c}_{i\alpha }}\left( {\mu {\partial _\alpha }\phi + {\rho _0}{{F}_{g\alpha }}} \right)}}{{{c^2}}}, $ | (1) |
| $ {g_i}\left( {{x + }{{c}_i}\Delta t,t + \Delta t} \right) - {g_i}\left( {{x},t} \right) = \frac{1}{{{\tau _g}}}\left( {{g_i}\left( {{x},t} \right) - g_i^{{\rm{eq}}}\left( {{x},t} \right)} \right), $ | (2) |
其中,角标i为离散的速度方向,α和β为空间坐标分量(β在后文中出现),x为格点位置,c为离散的格子速度,t为运动时刻,Δt为时间步长;ωi为权系数,μ为化学势,Fg为外力对应的加速度;ϕ=(ρA-ρB)/2为两相界面示踪参数,ρ0=(ρA+ρB)/2为两相平均密度,A和B分别代表两相.
通过Chapman-Enskog展开,上述两个离散化的LB方程能够在二阶精度范围内很好地还原为宏观Navier-Stokes方程和Cahn-Hilliard方程(∂tφ+u·∇ϕ=M∇2μ).后者广泛地应用于相分离和扩散问题的过程描述,M为迁移率;在两相流问题中用于捕捉相界面的变化,并能很好的考虑大密度比(可超过1 000)的问题.因此,本文采用的模型能够很准确地模拟大密度比的两相流问题.
1.2 非牛顿流体的LBM实现在LBM中,粘度v与弛豫时间τf有如下关系:
| $ {\tau _f} = \frac{1}{2} + \frac{{3v}}{{c\Delta x}}. $ | (3) |
对于幂律流体,其运动粘度
| $ v = \frac{K}{\rho }{\gamma ^{n - 1}} = \frac{K}{\rho }{\left( {{S_{\alpha \beta }}{S_{\alpha \beta }}} \right)^{\left( {n - 1} \right)/2}}, $ | (4) |
其中,γ为剪切速率,Sαβ为应变张量,K为稠度系数,n为非牛顿指数.
并且依据文献[34-35],应变张量Sαυ与LBM中的分布函数有如下关系
| $ {S_{\alpha \beta }} = \frac{3}{{2\rho {\tau _f}{c^2}}}\sum\limits_i {{f_i}^{\left( 1 \right)}{e_{i\alpha }}{e_{i\beta }}} , $ | (5) |
其中,fi(1)为分布函数fi的一阶Chapman-Enskog展开分量,此处用其非平衡分布函数近似,即
| $ {f_i}^{\left( 1 \right)} \approx f_i^{{\rm{nep}}} = {f_i} - f_i^{{\rm{ep}}}. $ | (6) |
综合式(3)~(6),即可应用LBM求解单相幂律流体的流动.
对于多相非牛顿流体系统,两相界面处需要特殊处理,在得到界面两侧流体粘度vA和vB的基础上,本文依据两相界面示踪参数ϕ进行权重分配,保证界面处粘度v在两相间连续过渡
| $ v = {v_{\rm{A}}} + \frac{{\phi - {\phi _{\rm{A}}}}}{{{\phi _{\rm{B}}} - {\phi _{\rm{A}}}}}\left( {{v_{\rm{B}}} - {v_{\rm{A}}}} \right). $ | (7) |
至此,就建立了完整的多相非牛顿幂律流体LBM体系.
2 简单结构驱替分析为了分析驱替机理,本文设计了如图 1所示的简单结构驱替模型,计算格子数量为250×43,对应的实际物理尺度为25 mm×4.3 mm.底部直径d=5 mm的液滴以半圆形的初始状态放置,为减小入口边界效应的影响,设置其左边缘初始位置距入口7 mm;此外,在距入口15 mm处设置有一小的固体障碍,大小为0.4 mm×0.4 mm.上下均为固体壁面,采用Bounce-back边界条件;左边界为压力入口,右边界为压力出口,进出口压差ΔP=2 Pa,均采用Zou-He压力边界条件[36].
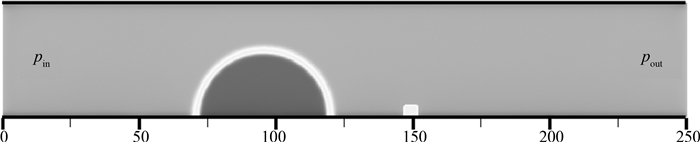 |
| 图 1 简单结构驱替模型 Fig.1 Simple structure displacement model |
驱替相(浅灰色)为非牛顿幂律流体,密度ρB=200 kg·m-3,静态粘度vB=1.8×10-4 m2·s-1,幂律指数n=0.9(剪切变稀),粘度系数K=0.02 Pa·sn;液滴(深灰色)为牛顿流体,作为被驱替相,密度ρA=900 kg·m-3,粘度vA=2.0×10-5m2·s-1.
2.1 牛顿流体与非牛顿流体驱替过程比较首先比较牛顿流体与非牛顿流体驱替过程.作为对照,牛顿驱替液粘度设置为与非牛顿驱替液静态粘度相同vN=1.8×10-4m2·s-1,其他物性参数与非牛顿驱替液相同.在此小节中,两相流体之间的界面张力σ=0.004 N·m-1,与固体之间都为中性润湿,即静态接触角θ=90°.定义驱替过程中三个临界时刻,分别为接触时刻(液滴右边界与障碍左侧接触瞬时)、越过时刻(液滴右边界与障碍右侧分离瞬时)和脱离时刻(液滴左边界与障碍右侧分离瞬时),对应于图 2所示的三种状态.
 |
| 图 2 驱替过程中三个临界状态 Fig.2 Three critical stateduring displacement |
图 3给出了牛顿流体驱替过程中液滴不同时刻的位置和形态.在所给定的压力下,液滴最终不能脱离障碍,而是经历接触(t=2.47 s)、越过(t=8.17 s)障碍两个阶段后,达到一稳定形态(t=14 s)吸附于障碍右侧,未能被成功驱替.应指出,若压力增大,液滴是有可能被成功驱替的.
 |
| 图 3 牛顿流体驱替过程 Fig.3 Newtonian fluid displacement |
图 4给出了非牛顿流体驱替过程中液滴不同时刻的位置和形态.在所给定的压力下,最终液滴能脱离障碍,被成功驱替.从开始运动到被成功驱替,整个过程用时14 s,接触障碍时刻为t=1.27 s、越过障碍时刻为t=4.07 s.
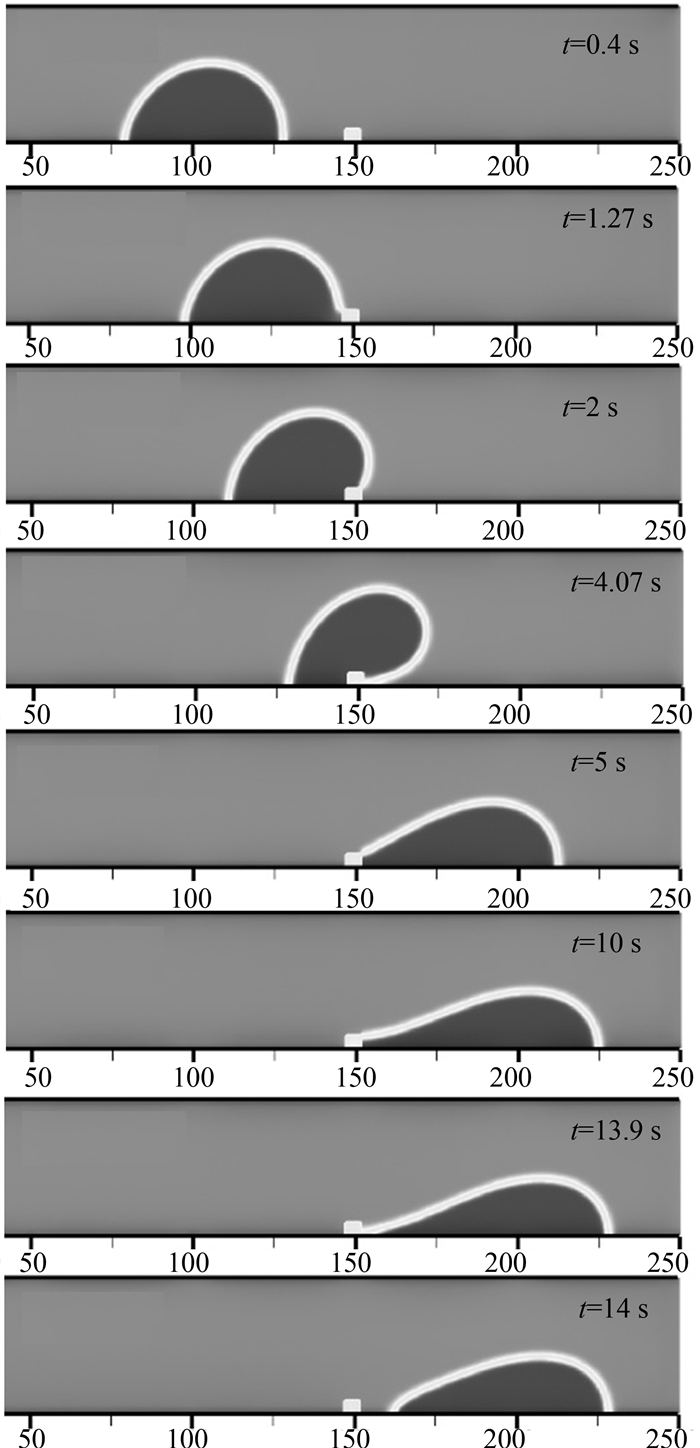 |
| 图 4 非牛顿流体驱替过程 Fig.4 Non-Newtonian fluid displacement |
比较图 3和图 4,可以得到:相比于牛顿流体,剪切变稀幂律流体驱替速度更快(接触障碍和越过障碍两个阶段所需时间分别缩短48.6%和50.2%),并且最终在所给定的压力下能成功驱替液滴.这是由于流体运动之后,流体的粘性会使其受到粘滞力作用,阻碍运动.对于牛顿流体,流动过程中其粘度不变;而对于剪切变稀幂律流体,其粘度随剪切速率增大而减小.进而对于静态粘度相同的两类驱替液,在同一剪切速率下,幂律驱替液所受到的流动阻力小于牛顿流体,因此其驱替能力更强.
2.2 界面张力对非牛顿流体驱替过程的影响界面张力是多相流问题中十分关键的参数之一,本小节详细讨论不同界面张力对非牛顿流体驱替过程的影响.为分析机理,仍采用如图 1所示的简单结构非牛顿流体驱替模型,除界面张力σ外,其他参数均保持一致,两相流体与固体之间都为中性润湿,即静态接触角θ=90°.
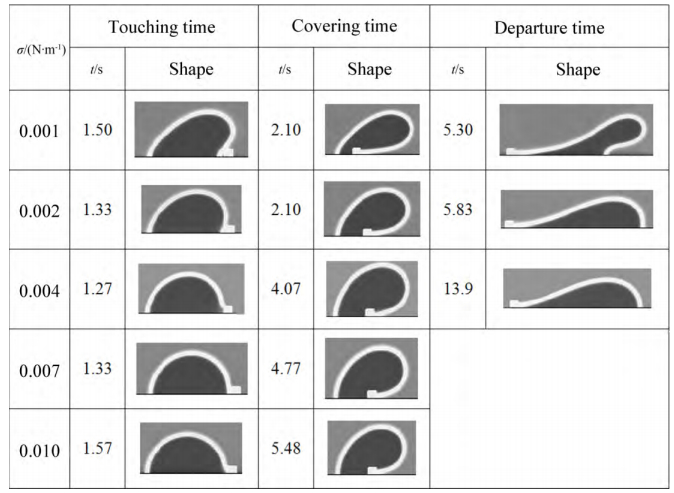
表 1比较了不同界面张力条件下,达到驱替过程中三个临界时刻所需时间及液滴对应的形态.对比几组临界时刻的液滴形态,观察到界面张力对于液滴运动形态的影响很大,界面张力越大,两相界面整体形状与圆弧形状越接近,随着界面张力的减小,界面形状的规则性越容易被破坏,形成较复杂的两相界面.这是因为界面张力是由同相流体内部分子吸引作用导致的,界面张力越大,表明内部吸引作用越强,越难被另一相流体干扰,从而整体上保持更规则的圆弧界面.
| 表 1 界面张力σ对非牛顿流体驱替过程的影响 Table 1 Impact of surface tension σ on non-Newtonian fluid displacement process |
 |
| 点击放大 |
另一方面,比较最终驱替成功所需的时间,可知界面张力越小,所需时间越短,随着界面张力增加,总驱替时间越长,甚至不能驱替成功.如图 5所示,分析越过和脱离两个阶段液滴所受的界面张力可知:在越过阶段,左侧界面张力几乎垂直,右侧则受到一个向左的界面长力;在脱离阶段则正好相反.因此,在驱替过程中,界面张力起阻碍液滴运动的作用,所以降低界面张力有助于提高驱替能力,减小总的驱替时间.
 |
| 图 5 驱替过程中的界面张力分析 Fig.5 Surface tension analysis during displacement |
同时注意到界面张力对接触障碍的时间影响并不大.这是由于在此算例中,液滴与固体之间为中性润湿,静态接触角为θ=90°,且在接触障碍之前,液滴运动缓慢,形变不明显,与固体壁面的动态接触角也都接近90°,界面张力的横向分量很小,因此界面张力对此阶段的影响不大.
3 多孔结构中非牛顿流体驱替过程模拟为了进一步研究实际复杂结构中的多相驱替过程,采用QSGS方法[37]生成了较为复杂的多孔结构,并构建了如图 6所示的复杂多孔结构驱替模型.总格子数量为200×52,对应的实际物理尺度为20 mm×5.2 mm,其中多孔结构区域大小为5 mm×5 mm,孔隙度为80%,初始时刻其孔隙完全由被驱替相填充.上下均为固体壁面,采用Bounce-back边界条件;左边界为压力入口,右边界为压力出口,均采用Zou-He压力边界条件[36].
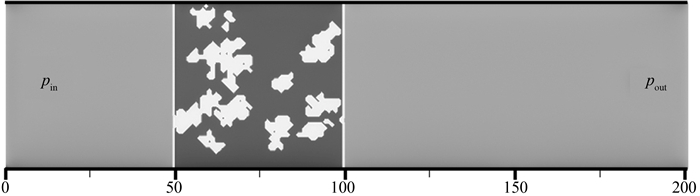 |
| 图 6 复杂多孔结构驱替模型 Fig.6 Porous structure displacement model |
驱替相(浅灰色)为非牛顿幂律流体,密度ρB=200 kg·m-3,静态粘度vB=1.8×10-4m2·s-1,幂律指数n=0.9(剪切变稀),粘度系数K=0.02 Pa·sn;被驱替相(深灰色)为牛顿流体,密度ρA=900 kg·m-3,粘度vA=2.0×10-5 m2·s-1.
3.1 压差和界面张力对非牛顿流体驱替过程的影响首先比较三组不同压差和界面张力参数下的驱替过程,如图 7所示(流体与固体之间设置为中性润湿,静态接触角θ=90°).三组结果中,图 7(a)和图 7(c)组中的大部分被驱替相能够被成功驱替,而图 7(b)组中的被驱替相最终与多孔结构形成附着,不能被驱替.对比图 7(b)和图 7(c)组,可以得到在相同界面张力下,提高压差的确能够提高驱替能力.对比图 7(a)和图 7(b)组,可以得到在压差下,减小界面张力也能够提高驱替能力,根据2.2节的机理分析,这一方面是由于界面张力在整个驱替过程中起阻碍作用,另一方面是由于低界面张力的流体更易于发生形变,在不规则的孔隙中的流动性更强.
 |
| 图 7 不同压差和界面张力参数下驱替过程对比 Fig.7 Displacement under various pressure difference and surface tension |
此外,在实际问题中,流体对固体的润湿特性也十分重要,因此在本小节详细讨论不同润湿性对非牛顿流体驱替过程的影响.图 8比较了三种不同润湿特性下非牛顿流体的驱替过程,分别为:被驱替相润湿(静态接触角θ=60°),中性润湿(静态接触角θ=90°)和驱替相润湿(静态接触角θ=120°).其他模拟条件均为:压差ΔP=20 Pa,界面张力σ=0.01 N·m-1.
 |
| 图 8 不同润湿特性下驱替过程对比 Fig.8 Displacement under different wettability |
从结果中可以看出,在该压差和界面张力下,三组中的大部分被驱替相都能被成功驱替,但图 8(a)组最终残余的被驱替相明显更多,并且从驱替时间来比较,图 8(a)组所需时间最多,其次是图 8(b)组,而图 8(c)组最快.这是因为润湿性好的液体更容易附着在固体表面,而润湿性差的会更容易被排挤离开固体表面.在图 8(a)组中,被驱替相的润湿性比驱替相的润湿性好,驱替相更容易附着在固体表面,难以被驱替;而在图 8(c)组中,驱替相的润湿性比被驱替相的润湿性好,驱替相更容易占据固体表面,并排挤被驱替相.因此,在相同的界面张力和压差下,提高驱替相的润湿特性(增加被驱替相的静态接触角)能够提高驱替能力.
根据上述分析,不难得出在实际应用中,提高压差,降低界面张力或是增加驱替相的润湿性都能够提高驱替能力.但是提高压差意味着增加功耗,需要更多的能源输入;而往往通过少量的添加剂进行调节,即可降低体系的界面张力或增强驱替相的润湿特性,所以后两种方法更为经济.
4 结论将非牛顿幂律流体模型引入多相LBM,建立了介观尺度分析多孔介质中非牛顿多相流体输运规律的数值计算框架,对多相非牛顿流体的驱替过程进行研究.相比于基于Darcy定律建立的传统方法,本文建立的数值计算框架能更好地捕捉过程中的流动细节,从而分析流动机理.通过比较牛顿流体和幂律流体的驱替过程,发现对于相同静止粘度的两种驱替液,由于流动过程中粘度不断减小,剪切变稀幂律流体的驱替能力更强,能更快地驱替管道中液滴.基于简单结构模型中非牛顿流体在不同界面张力参数下的驱替过程分析,得出界面张力在驱替过程中起阻碍作用,其它参数相同时,界面张力越低,流体的驱替能力越强.最后,多孔复杂结构内的非牛顿多相驱替过程模拟表明,提高压差,降低界面张力或是增加驱替相的润湿性都能够提高驱替能力;但相比于提高压差,降低体系的界面张力和增加驱替相的润湿性的方法可以节省能源,更为经济.为了结合实际应用,后续工作将进行三维驱替过程模拟,并考虑更多类型的非牛顿流体体系.
| [1] | FUERSTMAN M, GARSTECKI P, WHITESIDES G M. Coding/decoding and reversibility of droplet trains in microfluidic networks[J]. Science , 2007, 315 (5813) :828–832. doi:10.1126/science.1134514 |
| [2] | PRAKASH M, GERSHENFELD N. Microfluidic bubble logic[J]. Science , 2007, 315 (5813) :832–835. doi:10.1126/science.1136907 |
| [3] | THEBERGE A, COURTOIS F, SCHAERLI Y, et al. Microdroplets in microfluidics:An evolving platform for discoveries in chemistry and biology[J]. Angewandte Chemie International Edition , 2010, 49 (34) :5846–5868. doi:10.1002/anie.200906653 |
| [4] | KELLY B, BARET J, TALY V, GRIFFITHS A. Miniaturizing chemistry and biology in microdroplets[J]. Chemical Communications , 2007 (18) :1773–1788. doi:10.1039/b616252e |
| [5] | ZHENG B, ROACH L, ISMAGILOV R. Screening of protein crystallization conditions on a microfluidic chip using nanolitersize droplets[J]. Journal of the American Chemical Society , 2003, 125 (37) :11170–11171. doi:10.1021/ja037166v |
| [6] | SONG H, TICE J, ISMAGILOV R. A microfluidic system for controlling reaction networks in time[J]. Angewandte Chemie , 2003, 115 (7) :792–796. doi:10.1002/ange.200390172 |
| [7] | CYGAN Z, CABRAL J, BEERS K, AMIS E. Microfluidic platform for the generation of organic-phase microreactors[J]. Langmuir , 2005, 21 (8) :3629–3634. doi:10.1021/la0471137 |
| [8] | BRILL J. Multiphase flow in wells[J]. Journal of Petroleum Technology , 1987, 39 (1) :15–21. doi:10.2118/16242-PA |
| [9] | LENORMAND R, TOUBOUL E, ZARCONE C. Numerical models and experiments on immiscible displacements in porous media[J]. Journal of Fluid Mechanics , 1988, 189 (4) :165–187. |
| [10] | THORMAS S. Enhanced oil recovery-an overview[J]. Oil & Gas Science and Technology-Rev IFP , 2008, 63 (1) :9–19. |
| [11] | HAJIBEYGI H, JENNY P. Multiscale finite-volume method for parabolic problems arising from compressible multiphase flow in porous media[J]. Journal of Computational Physics , 2009, 228 (14) :5129–5147. doi:10.1016/j.jcp.2009.04.017 |
| [12] | NORDBOTTEN J. Adaptive variational multiscale methods for multiphase flow in porous media[J]. Multiscale Modeling & Simulation , 2009, 7 (3) :1455–1473. |
| [13] | NATVIG J, LIE K. Fast computation of multiphase flow in porous media by implicit discontinuous Galerkin schemes with optimal ordering of elements[J]. Journal of Computational Physics , 2008, 227 (24) :10108–10124. doi:10.1016/j.jcp.2008.08.024 |
| [14] | JENNY P, LEE S, TCHELEPI H. Adaptive fully implicit multi-scale finite-volume method for multi-phase flow and transport in heterogeneous porous media[J]. Journal of Computational Physics , 2006, 217 (2) :627–641. doi:10.1016/j.jcp.2006.01.028 |
| [15] | JENNY P, LEE S, TCHELEPI H. Adaptive multiscale finite-volume method for multiphase flow and transport in porous media[J]. Multiscale Modeling & Simulation , 2005, 3 (1) :50–64. |
| [16] | LUNATI I, JENNY P. Multiscale finite-volume method for compressible multiphase flow in porous media[J]. Journal of Computational Physics , 2006, 216 (2) :616–636. doi:10.1016/j.jcp.2006.01.001 |
| [17] | JUANES R. A variational multiscale finite element method for multiphase flow in porous media[J]. Finite Elements in Analysis and Design , 2005, 41 (7) :763–777. |
| [18] | PESZEYNSKA M, WHEELER M, YOTOV I. Mortar upscaling for multiphase flow in porous media[J]. Computational Geosciences , 2002, 6 (1) :73–100. doi:10.1023/A:1016529113809 |
| [19] | KIM J, DEO M. Finite element, discrete-fracture model for multiphase flow in porous media[J]. AIChE Journal , 2000, 46 (6) :1120–1130. doi:10.1002/(ISSN)1547-5905 |
| [20] | BLUNT M. Flow in porous media-pore-network models and multiphase flow[J]. Current Opinion in Colloid & Interface Science , 2001, 6 (3) :197–207. |
| [21] | CHEN S, DOOLEN G. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics , 1998, 30 (1) :329–364. doi:10.1146/annurev.fluid.30.1.329 |
| [22] | AIDUN C, CLAUSEN J. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics , 2010, 42 (1) :439–472. doi:10.1146/annurev-fluid-121108-145519 |
| [23] | WANG M, KANG Q. Electrokinetic transport in microchannels with random roughness[J]. Analytical Chemistry , 2009, 81 (8) :2953–2961. doi:10.1021/ac802569n |
| [24] | WANG M. Structure effects on electro-osmosis in microporous media[J]. Journal of Heat Transfer , 2012, 134 (5) :051020. doi:10.1115/1.4005711 |
| [25] | GUNSTENSEN A, ROTHMAN D, ZALESKI S, ZANETTI G. Lattice Boltzmann model of immiscible fluids[J]. Physical Review A , 1991, 43 (8) :4320–4327. doi:10.1103/PhysRevA.43.4320 |
| [26] | GUNSTENSEN A, ROTHMAN D. Lattice-Boltzmann studies of immiscible two-phase flow through porous media[J]. J Geophys Res , 1993, 98 (B4) :6431–6441. doi:10.1029/92JB02660 |
| [27] | SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E , 1993, 47 (3) :1815–1819. doi:10.1103/PhysRevE.47.1815 |
| [28] | SWIFT M, OSBORN W, YEOMANS J. Lattice Boltzmann simulation of nonideal fluids[J]. Physical Review Letters , 1995, 75 (5) :830–833. doi:10.1103/PhysRevLett.75.830 |
| [29] | HE X, CHEN S, DOOLEN G. A novel thermal model for the lattice Boltzmann method in incompressible limit[J]. Journal Computational Physics , 1998, 146 (1) :282–300. doi:10.1006/jcph.1998.6057 |
| [30] | HE X, CHEN S, ZHANG R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J]. Journal of Computational Physics , 1999, 152 (2) :642–663. doi:10.1006/jcph.1999.6257 |
| [31] | INAMURO T, OGATA T, TAJIMA S, KONISHI N. A lattice Boltzmann method for incompressible two-phase flows with large density differences[J]. Journal Computational Physics , 2004, 198 (2) :628–644. doi:10.1016/j.jcp.2004.01.019 |
| [32] | ZHENG H W, SHU C, CHEW Y T. A lattice Boltzmann model for multiphase flows with large density ratio[J]. Journal of Computational Physics , 2006, 218 (1) :353–371. doi:10.1016/j.jcp.2006.02.015 |
| [33] | HUANG J J, SHU C, CHEW Y T. Mobility-dependent bifurcations in capillarity-driven two-phase fluid systems by using a lattice Boltzmann phase-field model[J]. International Journal for Numerical Methods in Fluids , 2009, 60 (2) :203–225. doi:10.1002/fld.v60:2 |
| [34] | ARTOLI A. Mesoscopic computational haemodynamics[D]. Amsterdam, Netherlands:University van Amsterdam, 2003. |
| [35] | CHEN S, HE X, BERTOLA V, WANG M. Electrokinetic flow of non-Newtonian fluid in porous media[J]. Journal of Colloid and Interface Science , 2014, 436 :186–193. doi:10.1016/j.jcis.2014.08.048 |
| [36] | ZOU Q, HE X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids , 1997, 9 (6) :1591–1598. doi:10.1063/1.869307 |
| [37] | WANG M, WANG J, PAN N, CHEN S. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media[J]. Physical Review E , 2007, 75 (3) :036702. doi:10.1103/PhysRevE.75.036702 |
 2016, Vol. 33
2016, Vol. 33

