| 逆Compton散射的MonteCarlo模拟 |
逆康普顿散射是低能光子与相对论电子发生康普顿散射后获得能量的过程,是X射线天文学和γ射线天文学重要的辐射过程[1].逆康普顿散射或康普顿散射造成的辐射转移就是康普顿化过程.虽然可以通过求解Kompaneets方程[2]来解决低能光子在非相对论热电子中的康普顿化问题[3],但它并不能处理涉及极端相对论碰撞的康普顿化问题.Monte Carlo (MC)模拟方法在处理复杂、带有统计意义的粒子辐射输运问题时显示出巨大优势[4-5].
1983年和1984年,Pozdnyakov等人[6]和Gorecki等人[7]利用MC模拟方法解决光子在均匀、各向同性分布的相对论电子内的康普顿化问题,得出光子经多次逆康普顿散射或康普顿散射后的出射谱;1997年,Hua[4]利用MC方法模拟非均匀介质的康普顿化过程.在一定范围内已经成功地利用MC方法解决了光子在相对论等离子体内的康普顿化问题,但他们的方法都有各自的适用范围、优缺点,在极端相对论碰撞情况下可能不适用或者计算成本很高.所以有必要整合和完善逆康普顿散射的MC模拟方法.
在MC模拟时需要考虑计算成本,在整个逆康普顿散射的模拟中,以较低的抽样费用来抽取电子速度和光子散射方向或能量的样本是难点,而电子速度分布抽样费用和光子散射方向或能量分布抽样效率在很大程度上决定整个模拟的计算时间.已有的电子速度分布抽样方法和光子散射方向或能量分布抽样方法(文献[6-7, 4])都有各自的局限性,完善电子速度分布抽样方法和光子散射能量分布抽样方法,分析各种抽样方法保持较高抽样效率的条件对降低计算成本具有重要的意义.本文的第二部分描述MC模拟方法.第三部分是数值计算和验证.
1 MC模拟方法 1.1 物理模型与基本方程 1.1.1 基本假定在半径为R的球形内充满着均匀、呈各向同性分布的相对论电子云,电子的速度分布函数为N(v),密度为Ne;温度为Tr的黑体辐射源位于球心处,源光子将作为种子光子参与逆康普顿散射过程;光子与电子的碰撞只有康普顿效应,粒子在两次碰撞之间按直线运动, 方向和能量均不改变;为了便于模拟逆康普顿的散射过程,采用限制抽样方法确定自由程.
1.1.2 基本方程康普顿总散射截面由克莱因-仁科公式给出
| $ \sigma \left( \varepsilon \right) = \frac{3}{4}{\sigma _{\rm{T}}}\frac{1}{\varepsilon }\left[ {\left( {1 - \frac{4}{\varepsilon } - \frac{8}{{{\varepsilon ^2}}}} \right)\ln \left( {1 + \varepsilon } \right) + \frac{1}{2} + \frac{8}{\varepsilon } - \frac{2}{{2{{\left( {1 + \varepsilon } \right)}^2}}}} \right], $ | (1) |
式中σT是汤姆逊散射截面,ε=x,x/2是以mc2为单位的入射光子的能量,m是电子静止质量,c是光速.光子的入射能量x/2与散射能量x′/2之比
| $ r = x/x' = 1 + \varepsilon \left( {1 - \cos {\psi _1}/2} \right), $ | (2) |
式中的ψ1为光子入射方向与出射方向之间的夹角.为方便起见,对处于电子静止系的物理量加下标“1”描述(除x、x′、ε外),处于散射后状态的物理量加上标“′”描述.
假设光子和以速度v沿着z轴运动的相对论电子发生逆康普顿散射.在实验室坐标系下,光子的入射能量和出射能量分别为E、E′,入射方向和出射方向分别为Ω、Ω′,光子在电子静止坐标系和实验室坐标系下的入射能量、出射能量由洛伦兹变换联系
| $ x/2 = E\gamma \left( {1 - \nu \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}/c} \right)/mc,\;\;\;\;x'/2 = E'\gamma \left( {1 - \nu \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} '}}/c} \right)/m{c^2}. $ |
康普顿散射微分截面由Klein-Nishina公式给出
| $ \frac{{{\rm{d}}{\sigma _1}}}{{{\rm{d}}{{\mathit{\Omega '}}_1}}} = \frac{{3{\sigma _{\rm{T}}}}}{{16\pi }}X{\left( {x'/x} \right)^2}, $ | (3) |
这里X=x/x′+x′/x+4(1/x-1/x′)+4(1/x-1/x′)2,dΩ′1=sinθ′1dθ′1dϕ′1,其中θ′1为光子散射方向和v的夹角,ϕ′1为它与z轴所形成的方位角,而dΩ′1为围绕光子运动方向的立体角元.
| $ \frac{{{\rm{d}}\sigma }}{{{\rm{d}}\mathit{\Omega '}}} = \frac{{3{\sigma _{\rm{T}}}}}{{16\pi }}X{\left( {E'/E} \right)^2}{\gamma ^2}{\left( {1 - \nu \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}/c} \right)^2}. $ | (4) |
对(4)式中的立体角dΩ′积分,可以得到在实验室参考系下的康普顿散射总截面[4]
| $ \sigma \left( x \right) = \frac{3}{4}{\sigma _{\rm{T}}}\frac{1}{x}\left[ {\left( {1 - \frac{4}{x} - \frac{8}{{{x^2}}}} \right)\ln \left( {1 + x} \right) + \frac{1}{2} + \frac{8}{x} - \frac{1}{{2{{\left( {1 + x} \right)}^2}}}} \right]. $ | (5) |
在实验室系内光子的散射能量和入射能量之间的关系为[4, 6-7]
| $ E' = E\left( {1 - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nu /c} \right)/\left[ {1 - \nu \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} '}}/c + E\left( {1 - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} '}}} \right)/\gamma m{c^2}} \right]. $ | (6) |
光子的状态参量包括空间位置、能量、运动方向和权重.以Si=(ri, hνi, Ωi, wi)(i=0, 1, 2,…)表示一个源光子在相对论电子云中经过i次碰撞后的状态,其中ri表示光子第i次碰撞后的位置;Ωi表示光子第i次碰撞后的运动方向;hνi表示光子第i次碰撞后的能量;wi表示光子第i次碰撞后的权重,假设w0=1.
1.2.1 确定初始状态s0以球心为原点建立一固定的直角坐标系,称之为实验室坐标系一.光子的位置和运动方向在这一坐标系下可以表示为:r0=(0, 0, 0)、Ω0=(1, 0, 0).具有辐射温度kTr、能量E=hν的源的光子数密度分布为[6]
| $ p\left( E \right) = {b^3}{E^2}{\left( {{{\rm{e}}^{bE}} - 1} \right)^{ - 1}}/2.404, $ | (7) |
其中b=1/kTr.对分布p(E)采用加抽样[6]方法便可抽取E0.
1.2.2 确定下一个碰撞点逆康普顿散射平均截面〈σ〉为[4]
| $ \left\langle \sigma \right\rangle = \int_1^\infty {{\rm{d}}\gamma } \int\limits_{ - 1}^1 {{\rm{d}}\mu \left( {1 - v\mu /c} \right)\sigma \left( x \right)N\left( \gamma \right)/2} , $ | (8) |
其中,N(γ)为电子能量概率密度(〈σ〉的计算见文献[6]);μ=cosθ=v·Ωi/v.平均自由程λi=1/Ne〈σ〉.设光子当前位置到边界的距离为li(沿着方向Ωi),则光子在第i次碰撞后,直接逃逸出去的概率P(li)=exp (-Ne〈σ〉li),权重wi=wi-1(1-P(li-1)),自由程[6-8] λi=-λiln[1-ξ1(1-P(li))](ζn是在(0, 1)范围内均匀分布的随机数,n为整数,下同),下一碰撞点位置ri+1=ri+λiΩi.
1.2.3 确定电子的动量或速度本文分析两种不同的电子速度分布抽样方法,第一种是以文献[7]给出的具有普遍适用性的直接法;第二种是文献[4, 6]采用的乘抽样方法.
方法1 直接抽样法
该方法文献[7]已经详细给出,由于采用文献[7]的方法在对下文的(11)式抽样时,x必须小于1010,而且还存在百分之二的最大误差(文献[7]公式A13-A15),导致三角余弦值u < -1.02,为了改进这一不足,本文改用求反函数的直接法来对(11)式抽样.
文献[7]公式(A9)推导出的是散射电子速率的概率密度函数,这里把其改写成以洛伦兹因子γ为随机变量的概率密度分布
| $ {p_1}\left( \gamma \right) = \frac{{N\left( \gamma \right){\gamma ^{ - 1}}{{\left( {{\gamma ^2} - 1} \right)}^{ - 1/2}}\left\{ {F\left[ {{x_2}\left( \gamma \right)} \right] - F\left[ {{x_1}\left( \gamma \right)} \right]} \right\}}}{{\int_1^\infty {N\left( \gamma \right){\gamma ^{ - 1}}{{\left( {{\gamma ^2} - 1} \right)}^{ - 1/2}}\left\{ {F\left[ {{x_2}\left( \gamma \right)} \right] - F\left[ {{x_1}\left( \gamma \right)} \right]} \right\}} }}, $ | (9) |
其中
| $ F\left( x \right) = \left\{ \begin{array}{l} {x^2}/6 + 0.047{x^3} - 0.03{x^4} + {x^2}/2\left( {1 + x} \right);\;\;\;\;\;\;0 \le x \le 0.5,\\ \left( {1 + x} \right)\ln \left( {1 + x} \right) - 0.94x - 0.009\;25;\;\;\;\;\;\;0.5 \le x \le 3.5,\\ \left( {1 + x} \right)\ln \left( {1 + x} \right) - 0.5x - 13.16\ln \left( {2 + 0.076x} \right) + 9.214;\;\;\;\;\;\;3.5 \le x \le \infty . \end{array} \right. $ | (10) |
由(9)式可求出洛伦兹因子的概率分布,然后采用线性插值的方法对其抽样便可得到γ.
在取得γ的基础上,随机变量X的样本值x可通过求解下式获取[7]
| $ F\left( x \right) = F\left[ {{x_1}\left( \gamma \right)} \right] + {\xi _2}\left\{ {F\left[ {{x_2}\left( \gamma \right)} \right] - F\left[ {{x_1}\left( \gamma \right)} \right]} \right\}. $ | (11) |
文献[7]采用函数近似的方法求(11)式的反函数也可以取得x,但会有百分之二的最大误差,导致μ≤-1.02,而且当x>1010时该方法不适用.为了提高计算精度和能够模拟高能的碰撞,可以直接求解方程(11),把所得的根作为X的样本值.调用数学计算软件里专门解方程的库函数,就可以轻易地完成这一任务.下面以调用Matlab的库函数fzero为例来说明这一过程:
1) 计算F=F[x1(γ)]+ξ2{F[x2(γ)]-F[x1(γ)]}.
2) If F(0)≤F≤F(0.5)调用fzero求解方程F1(x)=F (F1(x)为式(10)的第一式),
else if F(0.5)≤F≤F(3.5)调用fzero求解方程F2(x)=F(F2(x)为式(10)的第二式),
else if F(3.5)≤F调用fzero求解方程F3(x)=F(F3(x)为式(10)的第三式,变量x的取值范围为3.5≤x < x2(γ)).显然,即使对于x>1010的高能情况,本算法也适用,而且计算结果的精度也更高,这是本文对直接法的改进.
在取得x后,便可求出电子运动方向与光子运动方向之间的夹角余弦
| $ \cos \theta = c\left( {1 - m{c^2}x/2h{\nu _i}\gamma } \right)/v. $ | (12) |
电子运动方向的方位角φ在(0, 2π)范围内均匀分布,所以φ=2πξ3.
利用电子运动方向与光子运动方向的几何关系和Ωi在实验室坐标系一的表达式,就可以确定电子运动方向在实验室坐标系一的方向余弦.至此,电子速度完全确定.
方法2 乘抽样法
第二种是以解析方法为主的乘抽样方法.文献[6]给出的这种方法只有在低能碰撞下才能保持较高的抽样效率.这种方法经文献[4]完善后,在x的量级比较大情况下仍可以保持较高的抽样效率,但文献[4]并没有分析乘抽样方法的抽样效率.实际上,在一定条件下这种方法会不适用(抽样效率很低),而且分析该抽样方法的抽样效率也是一个难点,为此下面详尽地分析这种方法的抽样效率,从而给出本方法的适用范围.
散射电子动量的概率密度分布可写成乘分布形式[4]
| $ {p_1}\left( \mathit{\boldsymbol{p}} \right) = {k_1}f\left( \mathit{\boldsymbol{p}} \right)N\left( \mathit{\boldsymbol{p}} \right), $ | (13) |
其中
1) 从动量的概率密度N(p)抽取样本.由于p是各向同性的,其方向向量v0={v10, v20, v30}可以利用直接抽样法获得.而p的大小可以通过对概率密度N(p)或N(γ)抽样获得.对于两种常见分布的抽样方法:(1) 麦克斯韦分布,采用乘抽样方法[4, 6];(2) 幂律谱N(γ)=Kγ-β,先求出分布函数,然后对其使用求反函数的直接抽样法即可.
2) 设f(p)的最大值为M,if ξ4 < f(p)/M,上一步抽出的p可以作为样本值,else回到“1”.
从f(p)的表达式可知,f(p)是一个关于μ、νi、γ的三元函数f(μ, νi, γ);在其取得最大值时μ一定等于-1.所以f(-1, νi, γ)的最大值即是M.
计算表明:当νi一定且1016≤νi < 1019(单位为Hz)时, f (-1, νi, γ)在1.4 < γ≤11.2范围内取得最大值M(σT≤M≤2σT),并且只有一个极值点,在区间(1,γM)内单调递增,在区间(γM,∞)内单调递减(γM是f(-1, νi, γ)取得最大值时的电子洛伦兹因子);当νi一定且1019≤νi≤1030时,f(-1, νi, γ)的最大值在1.001≤γ≤1.4范围内取得,f(-1, νi, γ)也只有一个极值点,单调性质和光子频率较低时的情况类似;当νi一定且νi < 1016时,f(-1, νi, γ)的最大值为2σT.
为了直观地反映f(-1, νi, γ)的性质,图 1给出νi依次为1016、1018、1020、1022、1024、1026、1028时,f(-1, νi, γ)在1≤γ≤109范围内的变化.从图 1可以看出,γ一定时,νi越大,f(-1, νi, γ)越小,特别地,当γ>105,νi>1020时,f(-1, νi, γ)/M < 10-4,这意味着乘抽样的拒绝率可能很高,这一特点极大地降低乘抽样效率.
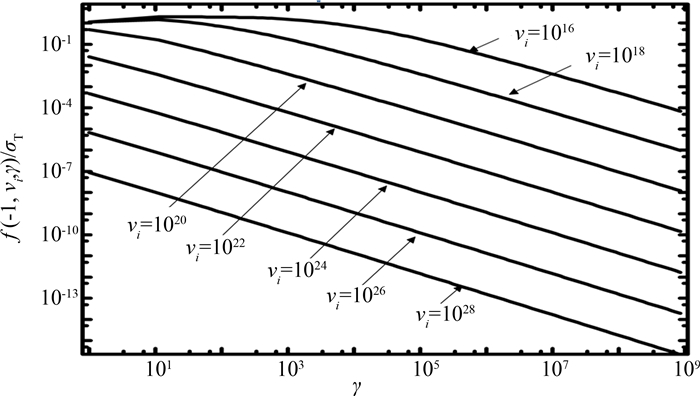 |
| 图 1 νi为1016、1018、1020、1022、1024、1026、1028时,f(-1, νi, γ)在1≤γ≤109范围内的变化 Fig.1 Variation of f(-1, νi, γ) as νi is 1016, 1018, 1020, 1022, 1024, 1026, 1028 and γ is in the rang of 1 to 109 |
由乘抽样效率公式E=1/k1M,可得E∝(λiM)-1.现在分析νi对E的影响,由于平均自由程λi随着νi的变大而变大,M却随着νi的变大而变小,所以νi对E的影响大小决定于两者贡献之和.但λi还和电子能量分布有关,所以要定量地算出E必须知道电子的能谱.
图 2给出了热电子谱(电子速度服从麦克斯韦分布)和幂律谱所对应的抽样效率随光子频率的变化.从图可知,对于麦克斯韦分布,光子频率和电子能量(n越大)越高,E就越小;对于幂律谱,E和能谱指数、能量的取值范围也有关,在相同条件下,β越小,E就越小;在β>1时,E大于0.1;在β < 1且ν不变时,γ从低能端到高能端之间的取值范围越大,E就越小;在β < 1且γ的取值范围一定时,ν越大,E就越小,并且在高频段已经非常之小.
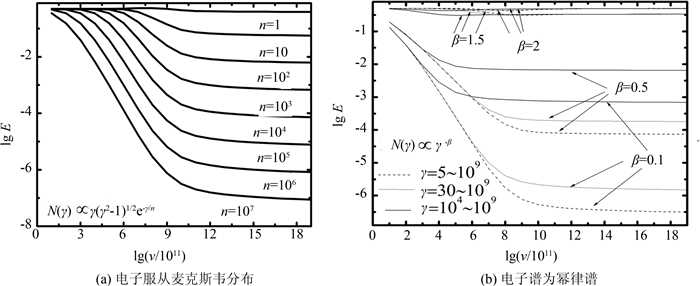 |
| 图 2 不同电子谱下,抽样效率随光子频率的变化 Fig.2 Selection efficiency E as functions of ν with different electronic distribution |
通过对图 1、图 2和乘抽样算法接受条件ξ5 < f(p)/M≤f(-1, νi, γ)/M的分析,可以得出低抽样效率的条件:光子能量比较高,连续分布的电子谱在低能区有定义并且γ的取值范围很广(γmax/γmin>105),电子密度分布函数值在整个高能段相对低能段仍较大.在图 2(a)的n很大和图 2(b)的β很小时(γmin也很小),高频段对应的E就属于这种情况.
从图 2和计算[6]可知在x
经过以上对抽样效率的分析,可以确定乘抽样方法的适用范围,从而完善这种抽样方法.
总体而言,第二种抽样方案相对简单明了,一般情况下作为首选,只有在抽样效率很低时采用直接法,后面将用计算证明这一点.
1.2.4 确定光子的散射方向和能量光子散射方向分布和能量分布的随机抽样方法有两种:一种是先从光子散射方向的概率密度函数抽取散射方向的样本[6-7],然后再从(6)式求出光子的散射能量;另一种是在电子静止系下采用乘加抽样方法抽取r,然后通过r求出散射能量、方向余弦,再把抽样所得的散射能量和方向余弦变换回实验室系[4].
方法1 在实验室系内的乘抽样法
文献[6]给出本方法简要的算法过程,文献[7]对整个抽样过程作了详细的推导.作为对文献[7]的补充,本文分析抽样效率,确定其适用范围.
1) 在电子静子系内计算μ′1=2ξ6-1;
2) 利用光行差公式把μ′1变回实验室系:μ′=(v/c+μ′1)/(1+vμ′1/c);
3) If ξ7 < X(x′/x)2/2,μ′可作为样本值,else回到“1)”.
抽样效率E(x)=2σ(x)/3σT,E随着x的增大而变小,如图 3所示.如取x=100,E(100)=0.025,可见这时的效率已经很低.所以本方法对于极端相对论碰撞不作为首选.散射方向与z轴(平行于v/v)的方位角ϕ′=2πξ8.利用光子散射方向与电子运动方向的几何关系就可以求出Ωi+1在实验室坐标系一的表达式.
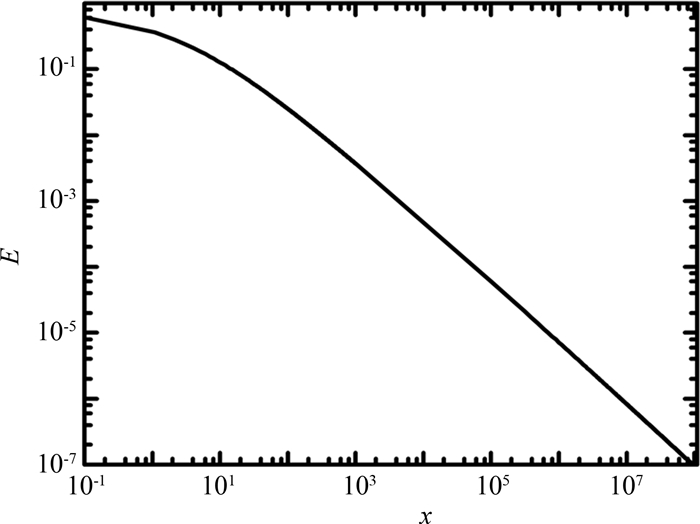 |
| 图 3 抽样效率E随x的变化 Fig.3 Sampling efficiency E as a function of x |
方法2 在电子静止系内的抽样方法文献[4]及文献[8]都介绍了这种抽样方法,通过对其抽样效率的分析知,文献[4]及文献[8]介绍的乘加抽样方法在ε>6 250时抽样效率已经很低.为了完善这种方法,降低计算费用,在ε>100时,本文对(14)式抽样采用求反函数的直接法.
以电子运动方向为z轴建立直角坐标系,称之为实验室坐标系二.在电子静止系也建立以电子运动方向为z′轴并和实验室坐标系二平行的坐标系,这两个坐标系中的物理量可以用特殊形式的洛伦兹变换相联系.实验室坐标系二的物理量又要变换到实验室坐标系一中,以实现对粒子位置的跟踪.
对(3)式立体角积分后可得到关于散射能量的微分散射截面
| $ f\left( r \right) = \left\{ \begin{array}{l} \left\{ {{{\left[ {\left( {\varepsilon + 2 - 2r} \right)/\varepsilon r} \right]}^2} + 1/r - 1/{r^2} + 1/{r^3}} \right\}/K\left( \varepsilon \right),\;\;\;\;\;\;1 \le r \le \varepsilon + 1,\\ 0,\;\;\;\;\;\;其它 \end{array} \right. $ | (14) |
上式中K(ε)=4εσ(ε)/3σT.对r的分布采用乘加抽样方法便可以得到r的样本值[4, 8].
该方法的抽样效率E=27(ε+1)K(ε)/2ε(2ε+29),E随ε的变化如图 4所示,当ε≈6时,E出现最大值,约为0.8,在ε < 1 000时抽样效率保持在比较高的水平;当ε>6,E不断地减小,在ε≈6 250处,E=0.01,抽样效率已经很低.
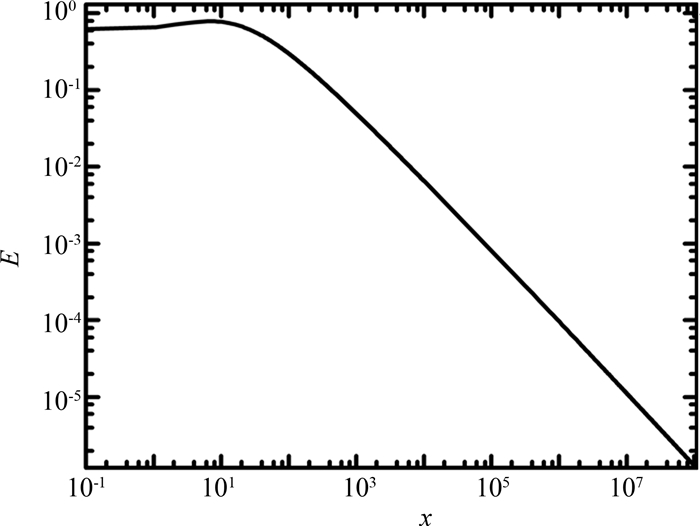 |
| 图 4 抽样效率E随ε的变化 Fig.4 Sampling efficiency E as a function of ε |
因为ε∝hνiγ/mc2,而在天体物理的高能辐射过程中,参与逆康普顿散射的种子光的能量与电子洛伦兹因子之积往往可超过10 000[9],所以有必要进一步完善上面给出的抽样方法.同样可采用求反函数的直接抽样法,具体过程如下:
1) 求出分布函数
| $ \begin{array}{l} f\left( r \right) = \left\{ {4r/{\varepsilon ^2} + \left( {1 - 4/\varepsilon + 4/{\varepsilon ^2}} \right)\ln r - \left[ {{{\left( {1 + 2/\varepsilon } \right)}^2} - 1} \right]/r - 1/2{r^2} - 1/2 - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left[ {4 - {{\left( {\varepsilon + 2} \right)}^2}} \right]/{\varepsilon ^2}} \right\}/K\left( \varepsilon \right),\;\;\;\;\;1 \le r \le \varepsilon + 1. \end{array} $ |
2) 借助方程求根算法求解方程F(r)=ξ9,把求出的根rroot作为样本值
可以对直接抽样法的使用界限设置一个判断阀值,从而将两种方法结合起来使用,比如阀值取100,当ε≤100时采用乘加抽样法,否则采用直接抽样法.
求得r后,便可以利用(2)式求出在电子静止系下的光子能量x/2和cosψ1.然后,由光行差公式求出在电子静止系中的入射角(入射光子运动方向与z轴间的夹角)余弦[10]cosθ1=(v·Ωi/v-v/c)/(1-v·Ωi/c).接着,利用球面三角公式cosψ1=cosθ1cosθ1′+sinθ1sinθ1′cos (ϕ-ϕ′)(方位角ϕ和ϕ′为洛伦兹不变量),即可求出光子散射角余弦cosθ1′.最后,再利用光行差公式求出实验室系下的光子散射角余弦cosθ′.
利用(6)式求出在实验室系下的散射能量后,状态参量hνi+1和Ωi+1都被确定了.
通过以上的分析可知,在实验室系内对光子散射方向分布抽样相对简单,对于x < 10的较低能的碰撞情况应该被首选;如果x≥10,应该在电子静止系内对光子散射能量分布抽样.
至此,光子的运动状态Si+1=(ri+1, hνi+1, Ωi+1, wi+1)已完全确定.
2 数值计算与验证理论分析表明[1, 6, 11]:在汤姆逊极限下,如果电子洛伦兹因子γ足够大,使得ν′=ν[1+4(γ2-1)/3]≈4γ2ν/3,而且电子能谱具有幂律形式或者麦克斯韦分布形式,那么,光子散射频率ν′(ν′
虽然本文计算所用的散射截面都是(5)式,但在一定程度上以上理论分析可以验证模拟结果是否正确.
下面的数值计算与验证主要涉及:①分别模拟麦克斯韦电子能谱、单幂律电子能谱所对应的辐射谱,然后把其谱指数和理论上的估计对比、把辐射谱与文献[6]给出的结果对比(主要是对比辐射谱的强度),以验证代码是否可行;②在得到相同计算结果的前提下,对比采用各种不同抽样方法所耗费的时间,以对上面关于抽样费用的计算分析进行验证.
2.1 电子服从麦克斯韦分布时的康普顿光谱图 5给出源位于球心处,源温度kTr=10-8mc2,电子云参数为n=4、τ=0.001,光子与电子散射次数为3,采用各种不同抽样方法所得的辐射谱:①电子速度抽样采用直接法,在电子静止系内对光子散射能量抽样;②电子速度抽样采用直接法,在实验室系对光子散射方向抽样;③电子速度抽样采用乘抽样(最大有效散射截面M随光子散射能量和电子能量的变化而变化)法,在电子静止系对光子散射能量抽样;④完全利用文献[6]的方法(最大有效散射截面M取固定值2σT,在实验室系内对光子散射方向抽样);⑤来自文献[6]的结果.从图可以看出,四种方法的结果都与文献[6]的结果高度相似,在τ
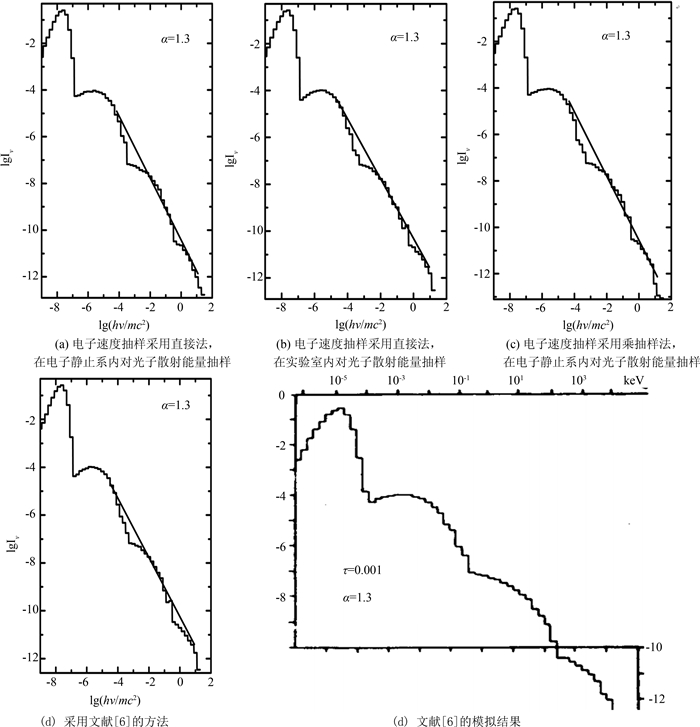 |
| 图 5 电子服从麦克斯韦分布时,采用不同抽样方法所得的辐射谱 Fig.5 Radiation spectrums obtained with different sampling methods for hot electrons |
在相同条件下(硬件条件:PC处理器AMD Athlon X2 240 2.80GHZ,内存2GB)模拟10 000光子的历史,利用四种不同方法所耗费的计算时间分别为:4分17秒、4分16秒、1分16秒、51秒.可见,对于较低能碰撞的情况,在实验室系内对光子散射方向分布抽样和在电子静止系内对光子散射能量分布抽样的计算时间相当;而电子速度抽样采用直接法会消耗更多的计算时间;文献[6]提供的方法最适用,因为按照上面对电子速度分布乘抽样效率的分析,n < 10和光子频率不太高的情况下,最大有效截面完全可以取固定值,这使得其与模拟图 5(c)的计算相比省去了求最值M的计算过程,但抽样效率仍达0.5.
2.2 电子谱为单幂律谱时的康普顿光谱图 6是源位于球心处,源温度分别为kTr=10-8mc2、kTr=10-4mc2,电子洛伦兹因子取为30 < γ < ∞,谱指数β=2,散射次数为1,采用不同方法所得的低频光子的单次散射谱:①电子速度抽样采用直接法,在电子静止系对光子散射能量抽样;②电子速度采用乘抽样方法,在电子静止系对光子散射能量抽样;③来自文献[6]的结果.从图可以看出:两种方法的计算结果几乎相同,和文献[6]所给的结果也很接近,只是文献[6]计算低温源的散射谱时采用了汤姆逊截面(本文引用到的其它的图的计算均用完全的散射截面),而本文的计算采用完全的散射截面,使得低温源的散射谱的强度比较小.显然,对于低温源的散射过程可认为是在汤姆逊极限下的,所以模拟结果与汤姆逊极限下的理论估计相一致,即在高频段谱指数都是0.5.对于高温源的散射谱,在一次散射谱的右侧(光子散射频率ν′
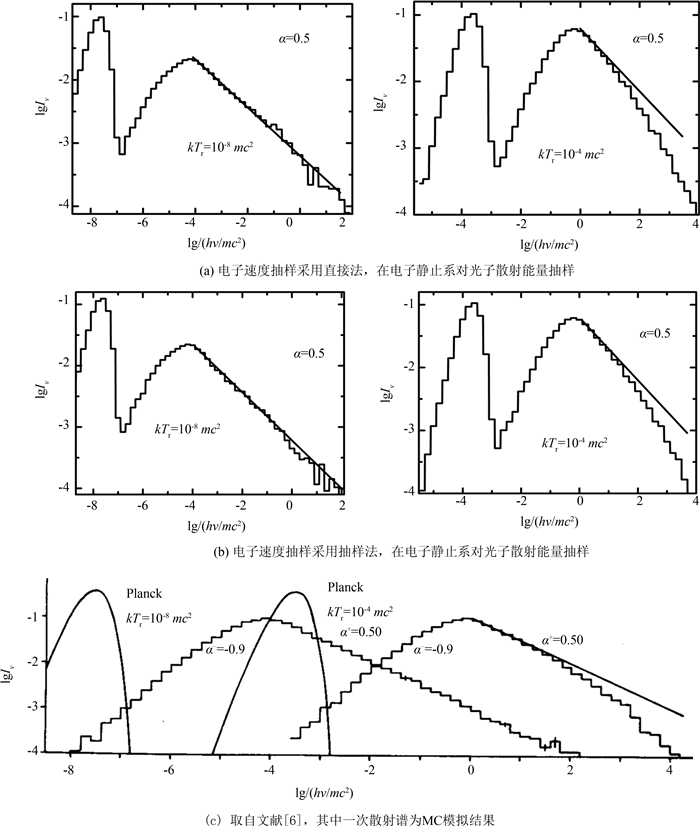 |
| 图 6 当源温度分别为10-8mc2、10-4mc2,电子谱为幂律谱(30≤γ≤∞),采用两种抽样方法所得的辐射谱 Fig.6 Radiation spectrums obtained with two sampling methods under conditions: kTr=10-8mc2, kTr=10-4mc2 and N(γ)=γ-2(30≤γ≤∞) |
在相同条件下模拟40 000个光子的历史,kTr=10-8mc2时,两种不同方法对应的计算时间分别为:16分13秒、10分2秒;kTr=10-4mc2时,计算时间分别为:16分45秒、10分20秒.这种结果和前面的抽样费用分析是一致的,因为在这种情况下图 2(b)给出的乘抽样方法的抽样效率比较高,而当采用直接法时,由于完成单次抽样需要相对较多的计算量,故总体的计算时间要比采用乘抽样法多.另外,由于β=2,乘抽样效率随源光子能量的增加而基本不变,所以两种源下的计算时间相差不大;直接法的计算费用本身就与源光子能量无关,所以两种情况下的计算时间非常接近.
图 7给出的是源位于球心处,源温度kTr=10-1mc2,散射次数为2,电子洛伦兹因子的取值范围为5 < γ < 108,谱指数为0.5,采用不同方法所得的辐射谱:①电子速度抽样采用直接法,在电子静止系对光子散射能量抽样;②电子速度采用乘抽样方法,在电子静止系对光子散射能量抽样.从图中可以看出:二重散射谱也有幂律谱型,但在大部分区域谱指数约为0.5,与理论估计值相差甚远.这是因为源光子的能量达不到汤姆逊极限的要求,由K-N截面主导的散射以及二重散射的影响使得汤姆逊极限下的谱指数估计理论不再适用.
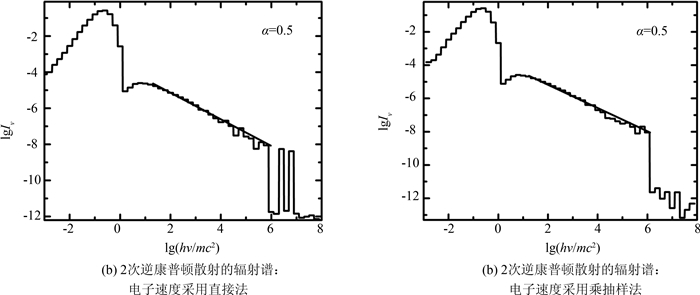 |
| 图 7 当源温度为10-1mc2,电子谱为幂律谱(5≤γ≤108 Fig.7 Radiation spectrums obtained with two sampling methods under conditions: kTr=10-1mc2 and N(γ)=γ-0.5(5≤γ≤108) |
在相同条件下采用两种不同的抽样方法模拟40 000个光子历史,所用的计算时间分别为:19分20秒、486分0秒,两者相差巨大!可见选择合适的抽样方法对节省计算时间的重要性.这一结果和上面的计算分析是相符合的,因为按照图 2(b),在这种情况下电子速度分布的乘抽样效率在光子的高频段非常低,而直接法的抽样费用和光子能量、电子谱分布基本无关.可见,在这种条件下,电子速度抽样采用直接法具有极大优势.表 1列出了在不同电子分布和辐射源下的各种抽样方案的计算时间.
| 表 1 不同电子分布、辐射源下的各种抽样方案的计算时间 Table 1 Caculation time of various sample plans with different electronic distribution and radiation source |
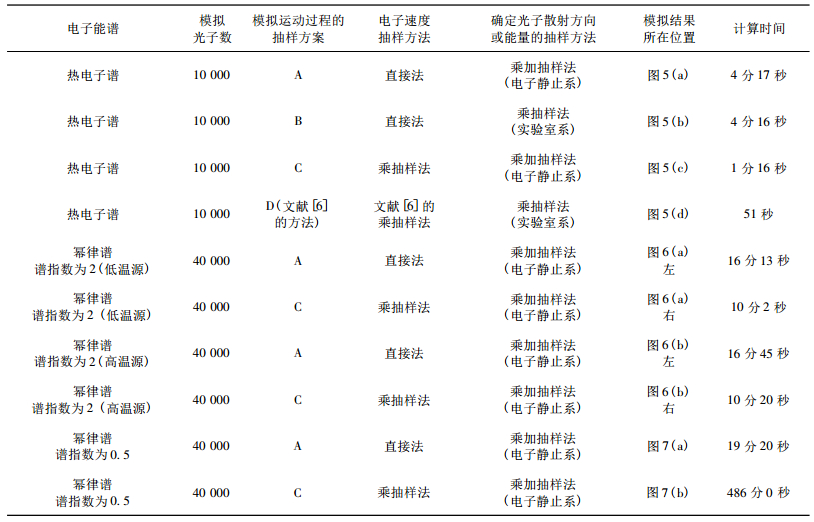 |
| 点击放大 |
1) 使用MC方法模拟黑体谱光子在均匀、各向同性球形相对论电子云中的康普顿化过程,所得的辐射谱谱型与理论分析基本符合,也与文献[6]的结果一致,验证了模拟方法的正确性.
2) 电子速度和光子散射能量或者方向的抽样费用对整个模拟费用的影响非常大.电子速度分布的乘抽样效率和光子的能量以及电子分布有关,一般情况下可以选择乘抽样方法对电子速度分布抽样,特别地,如果光子在电子静止系的能量x/2
3) 在经过求反函数的抽样方法完善电子速度抽样直接法和确定光子散射方向和能量的乘加抽样法后,这两种抽样方法适用于更高能的散射.在此基础上,采用已完善的乘加抽样法来确定光子能量和方向,并根据乘抽样方法抽样效率的分析结果选取合适的电子速度抽样方法(直接法或者乘抽样),以较低的计算费用模拟出高能的辐射谱,从而满足高能天体辐射的应用要求.
| [1] | 尤峻汉. 天体物理中的辐射机制[M].第二版. 北京: 科学出版社 , 1998 : 1 -408. |
| [2] | KOMPANEETS A S. The establishment of thermal equilibrium between quanta and electrons[J]. Soviet Physics JETP , 1957, 4 :730–737. |
| [3] | SUNYAEV R A, TITARCHUK L G. Comptonization of X-rays in plasma clouds -Typical radiation spectra[J]. Astrophysics , 1980, 86 (1) :121–138. |
| [4] | HUA X M. Monte Carlo simulation of Comptonization in inhomogeneous media[J]. Computational Physics , 1997, 11 (6) :1–17. |
| [5] | STERN B E, BEGELMAN M C, SIKORA M. A large-particle Monte Carlo code for simulating non-linear high-energy processes near compact objects[J]. MNRAS , 1995, 272 :291–307. doi:10.1093/mnras/272.2.291 |
| [6] | POZDNIAKOV L A, SOBOL I M, SIUNIAEV R A. Comptonization and the shaping of X-ray source spectra-Monte Carlo calculations[J]. Astrophysics and Space Physics Reviews , 1983, 2 :189–331. |
| [7] | GORECKI A, WILCZEWSKI W. A study of Compton of radiation in an electon plasma using the Monte Carlo method[J]. Acta Astronomica , 1984, 34 (2) :141–158. |
| [8] | 裴鹿成, 张孝泽. 蒙特卡罗方法及其在粒子输运问题中的应用[M].第一版. 北京: 科学出版社 , 1980 : 1 -550. |
| [9] | ZHENG Y G, KANG T. Evidence for secondary emission as the origin of hard spectra in Tev blazars[J]. ApJ , 2013, 764 :113–118. doi:10.1088/0004-637X/764/2/113 |
| [10] | YANG Chao, WANG Huihui, CHEN Ying, et al. Implementation of Monte Carlo collision algorithm in code CHIPIC[J]. Chinese J Comput Phys , 2012, 29 (5) :733–738. |
| [11] | GHISELLINI G. Radiative processes in high energy astrophysics[M]. arXiv:1202. 5949, 2012:94-97. |
 2016, Vol. 33
2016, Vol. 33


