| 同心壳层结构中超声速扩散辐射波的几何自由程 |
辐射输运在惯性约束聚变、天体物理及武器物理等领域都担当着重要角色[1-2],是高能量密度物理研究的重要内容.辐射输运的特性决定于辐射与物质原子之间的相互作用,同时与辐射传播速度是否超声速相关[3].对于辐射自由程相对很短的稠密物质,热波通常以亚声速传播,例如ICF靶丸的烧蚀热波[1];当物质的辐射自由程相对较长时,辐射会以超声速传播,例如激光ICF的固态黑腔[2]和Z箍缩的动(静)态黑腔[4].辐射输运过程可以用辐射输运方程[5]来描述,但通常情况下该方程的求解比较复杂和困难.采用扩散近似或者辐射热传导近似是对辐射输运方程进行简化处理的有效方法,在光学厚度较大的情况下,即使在扩散近似条件不严格成立的情况下也可适用[6].因此,人们往往避免大规模的辐射输运求解过程,而使用辐射扩散过程对物理问题进行分析和计算.
通常辐射自由程由物质吸收系数的平均而来,如光性厚情况下的Rosseland平均自由程和光性薄情况下的Plank平均自由程[7].在某些情况下,辐射平均自由程比传输通道的几何线度大得多,这时光子寿命主要取决于光子与固壁的碰撞,因此几何线度和特征是影响辐射能流大小的重要因素.在有限空间中则需要采用对横截面平均的辐射能流或简化模型得到与径向位置无关的几何自由程来描述器壁对光子的束缚作用.在简单的几何构型下,如光子在无限大平板夹层间的传播, 可以在直角坐标系中推导出辐射能流的近似解析结果[8],这种情况下几何自由程可取2ΔR0到8ΔR0/3,其中ΔR0为平板之间的距离的一半;对于柱形管中的辐射流传播也有了很好的研究结果[9],它的几何自由程更接近2ΔR0,并且给出随径向位置变化的修正方法,其中ΔR0为柱输运管的半径.
借鉴文献[8]关于直角坐标系下两平板间和文献[9]关于柱输运管中粒子传输的辐射能流计算的理论模型,本文将其理论模型运用到同心柱和同心球壳层结构中,给出壳层输运通道径向位置变化的谱辐射能流的计算公式,并分析其随径向位置变化的物理特性,同时给出不同壳层结构对应的几何自由程及修正因子.基于两同心球之间辐射输运问题,用类似的方法给出几何自由程计算方法和数值解并给出分析结果,最后基于严格数值计算结果给出便于应用的几何自由程拟合公式.
1 辐射能流的简化处理设fν(k, r, t)为空间r处t时刻,单位相空间一个量子态上沿Ω方向上传播的频率为ν的光子数,其中k=kΩ,c=2πν/k是光速,立体角Ω=Ω(θ, φ).设物质处于局部的热平衡,并忽略扩散过程,这样光的输运方程为
| $ \frac{{\partial {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right)}}{{\partial t}} + c\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right) = c{k'_\nu }\left( {{f_{\nu ,p}}\left( {\mathit{\boldsymbol{k}},r,t} \right) - {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right)} \right), $ | (1) |
其中fν, p=[exp (hν/kT)-1]-1,是物质温度为T时的Planck谱分布函数;k′ν为有效吸收系数.上式可用派尔斯积分形式写为
| $ \begin{gathered} {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right) = \int\limits_0^\infty {{{k'}_\nu }\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s,t - s/t} \right)} {f_{\nu ,p}}\left( {\mathit{\boldsymbol{k}},\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s,t - s/t} \right) \hfill \\ \exp \left( { - \int\limits_0^\infty {{{k'}_\nu }\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s,t - s'/t} \right)} {\rm{d}}s'} \right){\rm{d}}s, \hfill \\ \end{gathered} $ | (2) |
其中s是逆Ω方向上某点距r的距离,这样在r处s=0.
设τ=k′νs,则dτ=k′νds,由于光速很快,假设物质性能的变化在推迟时间s/c内可以忽略,则(2)式可写为
| $ \begin{array}{l} {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right) \approx \int\limits_0^\infty {{f_{\nu ,p}}\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s,t} \right){{\rm{e}}^{ - \tau }}{\rm{d}}\tau } = \hfill \\ \int\limits_0^\infty {\left[ {{f_{\nu ,p}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{t}}} \right) + \int\limits_0^s {\frac{{{\rm{d}}{f_{\nu ,p}}\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s',t} \right)}}{{{\rm{d}}s'}}{\rm{d}}s'} } \right]} {{\rm{e}}^{ - \tau }}{\rm{d}}\tau = \hfill \\ {f_{\nu ,p}}\left( {\mathit{\boldsymbol{r}},t} \right) + \int\limits_0^\infty {{{\rm{e}}^{ - \tau }}{\rm{d}}\tau } \int\limits_0^s {\frac{{{\rm{d}}{f_{\nu ,p}}\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}s',t} \right)}}{{{\rm{d}}s'}}{\rm{d}}s'} . \hfill \\ \end{array} $ | (3) |
注意到s在Ω的逆方向上,dfν, p/ds可写为
| $ \frac{{{\rm{d}}{f_{\nu ,p}}}}{{{\rm{d}}s}} = \frac{1}{{{{k'}_\nu }}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}{{k'}_\nu }. $ | (4) |
有两个同心的圆柱,其中外柱半径为R10,内柱半径R20,在两柱之间加入低密度光输运介质,这样的壳层作为光输运通道(如图 1(a)).假设外柱和内柱材料都为高Z介质,该介质中有效吸收系数k′ν很大,而在夹层的轻介质中k′ν很小由于光子主要在两同心柱间运动并沿z方向传输,因此温度T主要在z方向变化.设壳层宽度ΔR0=R10-R20,在垂直于轴心的圆环切面内,任意一点相对圆心的位置可用无量纲量ξ=r/R10来表示.柱的壳层结构和一般柱模型的主要区别在内柱器壁材料会吸收光子,导致空间某点接收到的辐射量降低.由图 1(b),在投影面上对于固定的ξ(r),直线BA与内圆相切,设直线BA与r的夹角为φ0(ξ),这里φ0(ξ)是ξ的函数,得到sinφ0(ξ)=R20/r=(1-ΔR0/R10)/ξ.当φ≤φ0时,在Ω的反方向光线和内柱外壁相交;φ>φ0时,Ω的任意反向延长线只和外柱内壁相交.于是可作以下近似
| $ {\left. {\frac{1}{{{{k'}_\nu }}}\nabla {f_{\nu ,p}}} \right|_{轻}}{\left. { \gg \frac{1}{{{{k'}_\nu }}} \cdot \nabla {f_{\nu ,p}}} \right|_{重}} \approx 0 $ | (5) |
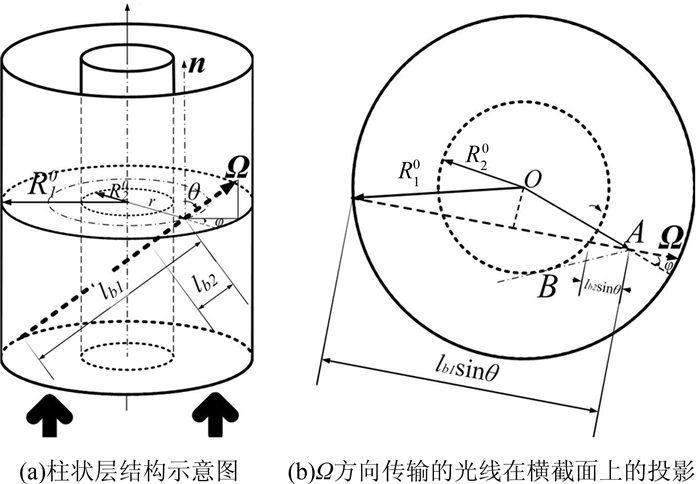 |
| 图 1 光子在两柱夹层中输运示意图 Fig.1 Photons transport between cylinder shell |
为了便于说明,下文中我们通过将长度变量除以光子物质自由程lν, m的方式将对应量无量纲化,仍用原来的符号,如R1即代表外圆半径除以物质自由程“R10/lν, m”, ΔR则代表夹层厚度除以物质自由程“(R10-R20)/lν, m”, 两者分别称为外圆柱径向光学厚度和圆柱壳层径向光学厚度.设lb1和lb2分别为点r沿Ω反方向到外柱内壁和内柱外壁的无量刚化的距离.式(4)可写为
| $ \int\limits_0^s {\frac{{{\rm{d}}{f_{\nu ,p}}}}{{{\rm{d}}s'}}} = - \int\limits_0^\tau \mathit{\Omega } \cdot \nabla {\rm{d}}{f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}{\rm{d}}\tau '{\rm{ = }}\left\{ \begin{gathered} \left\{ \begin{gathered} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}\tau ,\;\;\;\;\;\;\;\;\tau \leqslant {l_{\nu ,b2}}, \hfill \\ - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}{l_{\nu ,b2}},\;\;\;\;\;\tau > {l_{\nu ,b2}}, \hfill \\ \end{gathered} \right.\left| \varphi \right| \leqslant {\varphi _0}\left( \xi \right); \hfill \\ \left\{ \begin{gathered} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}\tau ,\;\;\;\;\;\;\;\;\tau \leqslant {l_{\nu ,b1}}, \hfill \\ - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}{l_{\nu ,b1}},\;\;\;\;\;\tau > {l_{\nu ,b1}}, \hfill \\ \end{gathered} \right.\left| \varphi \right| > {\varphi _0}\left( \xi \right); \hfill \\ \end{gathered} \right. $ | (6) |
设在r附近几个自由程区间内介质变化是均匀的,则可以认为从s=0开始的几个自由程内
| $ \int\limits_0^{{l_{\nu ,b2}}} {\tau {{\rm{e}}^{ - \tau }}{\rm{d}}\tau {\rm{ + }}{l_{\nu ,b2}}} \int\limits_{{l_{\nu ,b2}}}^\infty {{{\rm{e}}^{ - \tau }}{\rm{d}}\tau } = 1 - {{\rm{e}}^{ - {l_{\nu ,b2}}}},\;\;\;\;\;\;\left| \varphi \right| \leqslant {\varphi _0}\left( \xi \right); $ | (7) |
| $ \int\limits_0^{{l_{\nu ,b2}}} {\tau {{\rm{e}}^{ - \tau }}{\rm{d}}\tau {\rm{ + }}{l_{\nu ,b1}}} \int\limits_{{l_{\nu ,b2}}}^\infty {{{\rm{e}}^{ - \tau }}{\rm{d}}\tau } = 1 - {{\rm{e}}^{ - {l_{\nu ,b2}}}},\;\;\;\;\;\;\left| \varphi \right| > {\varphi _0}\left( \xi \right), $ | (8) |
得到
| $ {f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right) = \left\{ \begin{gathered} {f_\nu }\left( {r,t} \right) - {\left. {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}} \right|_{r,t}}\left( {1 - {{\rm{e}}^{ - {l_{\nu ,b2}}}}} \right),\;\;\;\;\;\;\left| \varphi \right| \leqslant {\varphi _0}\left( \xi \right); \hfill \\ {f_\nu }\left( {r,t} \right) - {\left. {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \cdot \nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}} \right|_{r,t}}\left( {1 - {{\rm{e}}^{ - {l_{\nu ,b1}}}}} \right),\;\;\;\;\;\;\left| \varphi \right| > {\varphi _0}\left( \xi \right). \hfill \\ \end{gathered} \right. $ | (9) |
根据几何关系,得到观测点到外柱和内柱的距离
| $ \begin{gathered} {l_{b1}} = \left( {\sqrt {R_1^2 - {r^2} + {r^2}{{\cos }^2}\varphi } + r\cos \varphi } \right)/\sin \theta = \\ {R_1}\left( {\sqrt {1 - {\xi ^2} + {\xi ^2}{{\cos }^2}\varphi } + \xi \cos \varphi } \right)/\sin \theta , \hfill \\ {l_{b2}} = \left( {r\cos \varphi - \sqrt {R_2^2 - {r^2} + {r^2}{{\cos }^2}\varphi } } \right)/\sin \theta = \\ {R_1}\left( {\xi \cos \varphi - \sqrt {{{\left( {1 - \beta } \right)}^2} - {\xi ^2} + {\xi ^2}{{\cos }^2}\varphi } } \right)/\sin \theta . \hfill \\ \end{gathered} $ | (10) |
平均每单位立体角上,与径向位置r相关的ν光子的谱辐射能流Fν为
| $ \begin{array}{l} {F_\nu } = \frac{1}{{4\pi }}\frac{{2h{\nu ^3}}}{{{c^2}}}\int\limits_\mathit{\Omega } {{f_\nu }\left( {\mathit{\boldsymbol{k}},r,t} \right)\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \hfill \\ = \left\{ \begin{gathered} \frac{1}{{4\pi }}\frac{{2h{\nu ^3}}}{{{c^2}}}\nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}\int\limits_\mathit{\Omega } {\left( {1 - {{\rm{e}}^{ - {l_{\nu ,b2}}}}} \right)\mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} ,\;\;\;\;\;\;\left| \varphi \right| \leqslant {\varphi _0}\left( \xi \right); \hfill \\ \frac{1}{{4\pi }}\frac{{2h{\nu ^3}}}{{{c^2}}}\nabla {f_{\nu ,p}}\frac{1}{{{{k'}_\nu }}}\int\limits_\mathit{\Omega } {\left( {1 - {{\rm{e}}^{ - {l_{\nu ,b1}}}}} \right)\mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} ,\;\;\;\;\;\;\left| \varphi \right| > {\varphi _0}\left( \xi \right); \hfill \\ \end{gathered} \right. \hfill \\ = \frac{1}{3}\frac{1}{{{{k'}_\nu }}}\nabla {I_{\nu ,p}} \cdot \mathit{\boldsymbol{Q}}\left( { - {l_{\nu ,b1}}, - {l_{\nu ,b2}},\xi } \right), \hfill \\ \end{array} $ | (11) |
其中
| $ \mathit{Q}\left( { - {l_{\nu ,b1}}, - {l_{\nu ,b2}},\xi } \right) = \left\{ \begin{gathered} I - \frac{1}{{4\pi }}\int\limits_\mathit{\Omega } {{{\rm{e}}^{ - {l_{\nu ,b2}}}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} ,\;\;\;\;\;\;\left| \varphi \right| \leqslant {\varphi _0}\left( \xi \right); \hfill \\ I - \frac{1}{{4\pi }}\int\limits_\mathit{\Omega } {{{\rm{e}}^{ - {l_{\nu ,b1}}}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} ,\;\;\;\;\;\;\left| \varphi \right| > {\varphi _0}\left( \xi \right); \hfill \\ \end{gathered} \right. $ | (12) |
为总的几何因子.只考虑其在z方向的分量η(R1, ΔR, ξ),则
| $ \begin{array}{l} \eta \left( {{R_1},\Delta R,\xi } \right) = 1 - \frac{3}{\pi }\left[ {\int\limits_0^{{\varphi _0}\left( \xi \right)} {\int\limits_0^{\pi /2} {\exp \left( { - {R_1}\frac{{\xi \cos \varphi - \sqrt {{{\left( {1 - \Delta R/{R_1}} \right)}^2} - {\xi ^2} + {\xi ^2}{{\cos }^2}\varphi } }}{{\sin \theta }}} \right)} } } \right. \hfill \\ \sin \theta {\cos ^2}\theta {\rm{d}}\theta {\rm{d}}\varphi + \hfill \\ \left. {\int\limits_{{\varphi _0}\left( \xi \right)}^\pi {\int\limits_0^{\pi /2} {\exp \left( { - {R_1}\frac{{\sqrt {1 - {\xi ^2} + {\xi ^2}{{\cos }^2}\varphi } + \xi \cos \varphi }}{{\sin \theta }}} \right)} } \sin \theta {{\cos }^2}\theta {\rm{d}}\theta {\rm{d}}\varphi } \right]. \hfill \\ \end{array} $ | (13) |
由于我们只关心几何因素在对z方向传输能流的影响,因此后文中将z方向的分量η(R1, ΔR, ξ)泛称为几何因子,设s=sinθ,w=2φ/π则
| $ \int\limits_{2{\varphi _0}\left( \xi \right)/\pi }^1 {\int\limits_0^1 {\exp \left( { - {R_1}\frac{{\sqrt {1 - {\xi ^2}{{\sin }^2}\left( {\frac{\pi }{2}w} \right)} - \xi \cos \left( {\frac{\pi }{2}w} \right)}}{s}} \right)} } s\sqrt {1 - {s^2}} {\rm{dsd}}w $ | (14) |
为了说明几何因子η(R1, ΔR, ξ)在径向上的特性,我们固定壳层的光学厚度ΔR和外柱半径R1来考察η(R1, ΔR, ξ)随径向ξ的变化.图 2中给出了ΔR/R1=0.5时,柱壳的外半径为ΔR=0.1, 1, 2的情况下,几何因子η(R1, ΔR, ξ)在径向上的变化规律.由于器壁对光子的吸收作用,靠近柱壁时几何因子明显下降,从而在壳层中成拱形分布.图 2(a)和(b)中,壳层两端(外柱内侧和内柱外侧)的几何因子并不相等,计算表明对于较小的输运通道,内柱外侧附近的几何因子η(R1, ΔR, |ξ|=R2/R1)会明显小于外圆内侧附近的几何因子η(R1, ΔR, |ξ|=1),而且介质的光学厚度越小,该现象越明显,造成这个现象主要原因是内外柱腔壁不同的曲率半径.这样通过辐射输运作用使光子沉积在内外器壁上, 并对内(外)柱器壁造成影响的空间总体积产生差异.当输运通道的光学厚度较小时,输运通道内的所有空间都对观察点有作用,因此对外壁作用的空间体积大于对内壁作用的空间体积;相反,当通道的光学厚度很大时,器壁只能感受到其局域空间范围内光子的作用,因此差异很小(如图 2(c)).对于径向光学厚度ΔR很大的请况,远离腔壁的空间几乎不受腔壁吸收的影响,几何因子几乎不变,而只有距离腔壁比较近时才会受其影响,距离器壁2~3个物质自由程内的光子才能被吸收,此时几何因子会明显减小.以上分析是ΔR/R1=0.5的情况,对于ΔR→R1的平板极限和ΔR/R1→1的圆柱极限,其物理现象和图 2相似,都存在ΔR比较小时壳层输运道两侧几何因子的不对称性.
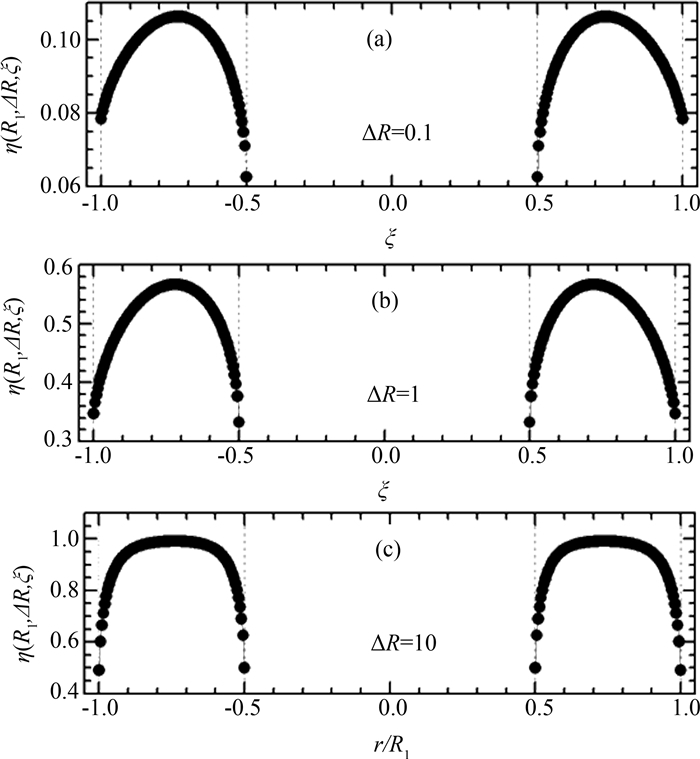 |
| 图 2 在ΔR=0.5R1的几何结构下,几何因子η(R, ΔR, ξ)随径向ξ的函数关系 Fig.2 Geometric factor η(R, ΔR, ξ) as functions of ξ as ΔR=0.5R1 |
我们计算对横截面平均的辐射能流和几何因子,并与文献给出的极限情况几何因子对比,将辐射能流对横截面求平均,得
| $ \overline {{F_\nu }} = \frac{{2\pi }}{S}\int\limits_{{R_2}}^{{R_1}} {{F_\nu }r{\rm{d}}r} = \frac{1}{3}\bar \eta \left( {\Delta R,{R_1}} \right){l_{\nu ,p}}\nabla {I_{\nu ,p}}, $ | (15) |
这里
| $ \begin{array}{l} \bar \eta \left( {{R_1},\Delta R} \right) = \frac{{2R_1^2}}{{\Delta R\left( {2{R_1} - \Delta R} \right)}}\int\limits_{1 - \Delta R/{R_1}}^1 {\eta \left( {{R_1},\xi } \right)\xi {\rm{d}}\xi } = \frac{{R_1^2}}{{\Delta R\left( {2{R_1} - \Delta R} \right)}}\left\{ {\frac{{\Delta R\left( {2{R_1} - \Delta R} \right)}}{{R_1^2}}} \right. - \hfill \\ 3\left[ {\int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } } \right.\int\limits_0^{2{\varphi _0}\left( \xi \right)/\pi } {{\rm{d}}w} \int\limits_0^1 {\exp \left( { - {R_1}\frac{{\xi \cos \frac{\pi }{2}w - \sqrt {{{\left( {1 - \Delta R/{R_1}} \right)}^2} - {\xi ^2}{{\sin }^2}\frac{\pi }{2}w} }}{s}} \right)} \hfill \\ s\sqrt {1 - {s^2}} {\rm{d}}\mathit{s} + \int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \int\limits_{2{\varphi _0}\left( \xi \right)/\pi }^1 {{\rm{d}}w} \int\limits_0^1 {\exp \left( { - {R_1}\frac{{\sqrt {1 - {\xi ^2}{{\sin }^2}\frac{\pi }{2}w} + \xi \cos \frac{\pi }{2}w}}{s}} \right)} \hfill \\ s\sqrt {1 - {s^2}} {\rm{d}}\mathit{s} + \int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \hfill \\ \left. {\left. {\int\limits_0^1 {{\rm{d}}w} \int\limits_0^1 {\exp \left( { - {R_1}\frac{{\sqrt {1 - {\xi ^2}{{\sin }^2}\frac{\pi }{2}w} + \xi \cos \frac{\pi }{2}w}}{s}} \right)} s\sqrt {1 - {s^2}} {\rm{d}}\mathit{s}} \right]} \right\}. \hfill \\ \end{array} $ | (16) |
对于平板和柱输运管,人们常用到以下的公式来表征平均几何因子[7-8],本文中也使用相同的定义
| $ \frac{1}{{{{\bar \eta }_e}{l_{\nu ,m}}}} = \frac{1}{{{l_{\nu ,m}}}} + \frac{1}{{e\Delta l}} \Rightarrow {{\bar \eta }_e} = \frac{1}{{1 + {l_{\nu ,m}}/e\Delta l}} = \frac{1}{{1 + 1/e\Delta R}}. $ | (17) |
该定义的含义为总的光学厚度ηelν, m等于物质自由程lν, m与几何自由程eΔl两者的“并联”效果,这里Δl和lν, m分别具有长度量纲的输运通道宽度和物质自由程,这样ΔR=Δl/lν, m即前面定义的用物质自由程无量纲化的壳层光学厚度.其中变量e是几何因子参数,它的物理含义为几何自由程相对输运通道径向宽度的倍数,只要确定几何因子参数e即可给出相应因子和几何自由程,后面我们主要针对几何因子参数e进行研究.例如,对于无穷大平板且光学厚度较大的情况对应e→8/3,这样对应的几何因子为:η8/3=[1+(8ΔR/3)]-1对于同心柱壳层模型,其结构完全不同于平板和圆柱结构,因此需要根据其结构重新修正.这时候我们提出的问题是对于确定的壳层光学厚度ΔR,参数e应该取多少才能很好地反映其几何约束效果?因此在式(17)基础上可以利用
| $ e = \frac{1}{{\left( {1/{{\bar \eta }_e} - 1} \right)\Delta R}} $ | (19) |
来确定几何因子参数,ηe则由方程(16)严格计算给出.图 3(a)给出了固定壳层长度和外柱半径比ΔR/R1的条件下几何因子参数e随输运通道的光学厚度ΔR的变化情况.点虚线对应ΔR/R1=1的完全圆柱极限情况,同时给出了文献[9]文中计算得到的结果作为比较(黑色的交叉点),圆柱计算结果与文献给出的结果完全吻合.黑色实线为ΔR/R1=0.02时的结果,这时对应内外柱半径非常接近平板极限(ΔR→R1),这时壳层内外器壁的曲率半径非常大.图中也标出了文献[8]中给出的平板模型计算结果作为对比(黑色圆圈点),这几个点和我们计算的平板极限曲线吻合也非常好,这说明ΔR/R1=0.02时柱壳层结构特性非常接近平板结构,同时也证明了我们理论计算的正确性.从图 3(a)中我们对几何因子参数的特性进行了总结,得到以下规律认识:①壳层光学厚度ΔR大于3个物质自由程时介质对光子的吸收是主导因素,器壁上光子的吸收对光子传输的影响较低,这时几何自由程比物质自由程大得多,几何因子
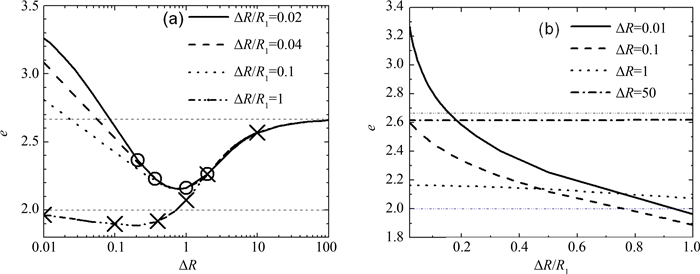 |
| 图 3 参数e随壳层光学厚度ΔR和几何结构ΔR/R1的变化 Fig.3 (a) Geometric factor e vs.optical thickness ΔR; (b) geometric factor e vs. geometric structure ΔR/R1 |
图 3(b)给出了对于不同的壳层光学厚度ΔR,几何因子参数e随柱几何结构ΔR/R1变化的规律(相当于变化外柱半径),体现外柱曲率变化对几何因子的影响.图的左端是R1=ΔR的圆柱情况,右端为R1
下面要研究的问题是两个同心的圆球模型,两球之间的壳层内填充低密度光输运介质作为光输运通道,考虑这样的几何结构对平均辐射的影响.为了讨论问题的方便,我们给圆球壳定一个方向,光从球壳的一端沿球壳传播到全空间,这样我们研究的问题便是轴对称性的.假设光子传播过程相对入射方向的轴线保持很好的对称性,则光子传播方向始终垂直于光子所在位置与过球心所确定的轴对称圆锥面,这个圆锥面就是我们研究辐射流所需要确定的截面.类似于方程(6)-(14),可以得到同心球结构下几何因子
| $ \begin{array}{l} \eta \left( {{R_1},\Delta R,\xi } \right) = \\ 1 - \frac{3}{2}\left[ {\int\limits_0^{\sin {\theta _0}} {\int\limits_0^1 {\exp {{\left( { - {R_1}\left( {s\xi \cos \left( {\frac{{e\pi }}{2}} \right) + \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}\cos \left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)}^2}} } } \right.s\sqrt {1 - {s^2}} {\rm{dsd}}w + \hfill \\ \int\limits_0^{\sin {\theta _0}} {\int\limits_0^1 {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}\cos \left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)} } s\sqrt {1 - {s^2}} {\rm{dsd}}w + \hfill \\ \int\limits_{\sin {\theta _0}}^0 {\int\limits_0^{2{\varphi _0}/\pi } {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) - \sqrt {{{\left( {1 - \beta } \right)}^2} - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)} } s\sqrt {1 - {s^2}} {\rm{dsd}}w + \hfill \\ \int\limits_{\sin {\theta _0}}^1 {\int\limits_{2{\varphi _0}/\pi }^1 {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) - \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)} } s\sqrt {1 - {s^2}} {\rm{dsd}}w + \hfill \\ \left. {\int\limits_{\sin {\theta _0}}^1 {\int\limits_0^1 {\exp \left( { - {R_1}\left( { - s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)} } s\sqrt {1 - {s^2}} {\rm{dsd}}w} \right]. \hfill \\ \end{array} $ | (20) |
图 4给出了不同光学厚度情况下,几何因子η(R1, ΔR, ξ)随径向的分布情况.球壳层情况下几何因子受器壁的影响比柱壳层更严重,由于球壁材料对辐射的吸收, 几何因子η(R1, ΔR, ξ)在球的壳层中成拱形分布.和柱壳结果相比,壳层光学厚度ΔR很小时,外球内侧的几何因子不会明显大于内球外侧,柱壳情况这种特征非常明显.另一点区别是曲线的最高点更偏向内球,这是由于几何结构的差别引起的.球壳层具有三维的封闭性,而柱壳层只在两维空间上具有约束.
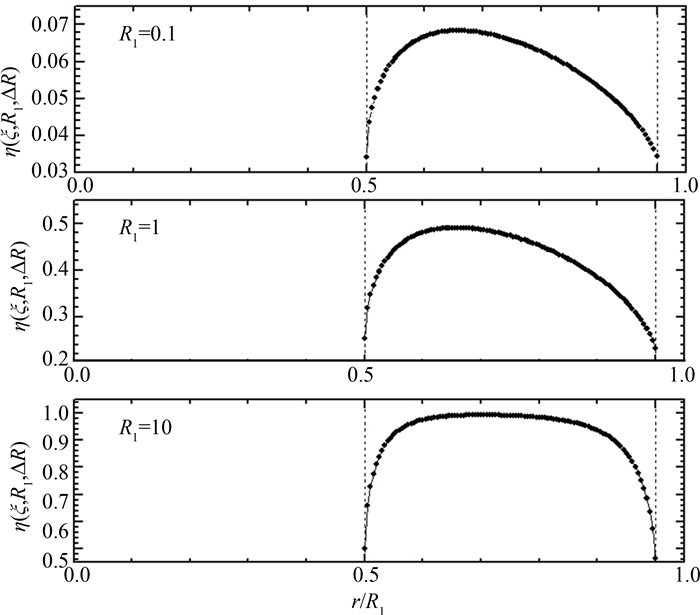 |
| 图 4 ΔR/R1=0.5的球壳层结构中,不同光学厚度情况下的几何因子η(R1, ΔR, r/R1)随径向ξ的函数关系 Fig.4 Geometric factor η(R, ΔR, ξ) as functions of ξ with spherical shell structure ΔR=0.5R1 |
类似于柱壳结构,平均几何因子η(R1, ΔR)是η(R1, ΔR, ξ)对横截面积平均的几何因子,由于介质内点r处的辐射Fν只是径向r的函数,而和角度ω无关,所以作面积平均时对任意的锥体张角ω均可,简单起见,选取ω=π/2所对应的平面, 这样面积为:
| $ \begin{array}{l} \bar \eta \left( {{R_1},\Delta R} \right) = \frac{{2R_1^2}}{{\Delta R\left( {2{R_1} - \Delta R} \right)}}\int\limits_{1 - \Delta R/{R_1}}^1 {\eta \left( {{R_1},\Delta R,\xi } \right)} \xi {\rm{d}}\xi = \\ \frac{{R_1^2}}{{\Delta R\left( {2{R_1} - \Delta R} \right)}}\left\{ {\frac{{\Delta R\left( {2{R_1} - \Delta R} \right)}}{{R_1^2}}} \right. - \hfill \\ 3\left[ {\int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } } \right.\int\limits_0^{\sin {\theta _0}} {{\rm{d}}w} \int\limits_0^1 {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \\ \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)} s\sqrt {1 - {s^2}} {\rm{d}}\mathit{w} + \hfill \\ \int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \int\limits_0^{\sin {\theta _0}} {{\rm{ds}}} \int\limits_0^1 {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \\ \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)s} \sqrt {1 - {s^2}} {\rm{d}}\mathit{w} + \hfill \\ \int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \int\limits_{\sin {\theta _0}}^1 {{\rm{ds}}} \int\limits_0^{2{\varphi _0}/\pi } {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \\ \sqrt {{{\left( {1 - \beta } \right)}^2} - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)s} \sqrt {1 - {s^2}} {\rm{d}}\mathit{w} + \hfill \\ \int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \int\limits_{\sin {\theta _0}}^1 {{\rm{ds}}} \int\limits_{2{\varphi _0}/\pi }^1 {\exp \left( { - {R_1}\left( {s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \\ \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)s} \sqrt {1 - {s^2}} {\rm{d}}\mathit{w} + \hfill \\ \left. {\int\limits_{1 - \Delta R/{R_1}}^1 {\xi {\rm{d}}\xi } = \int\limits_{\sin {\theta _0}}^1 {{\rm{ds}}} \int\limits_0^1 {\exp \left( { - {R_1}\left( { - s\xi \cos \left( {\frac{{w\pi }}{2}} \right) + \\ \sqrt {1 - {\xi ^2} + {\xi ^2}{s^2}{{\cos }^2}\left( {\frac{{w\pi }}{2}} \right)} } \right)} \right)s} \sqrt {1 - {s^2}} {\rm{d}}\mathit{w}} \right]. \hfill \\ \end{array} $ | (21) |
图 5给出了壳层光学厚度ΔR为0.1,1,10,50情况下,几何因子参数e随几何结构ΔR/R1变化的曲线.相对于柱壳层,在相同的内外半径情况下,球壳层器壁对应的曲率更大,并且由于球是完全封闭结构,光子会受到更强的三维约束.球壳层的几何因子参数有以下几方面的特性.①图上左端为ΔR/R1→0的平板近似情况,在这种极限下e接近8/3,但不会出现柱壳层中那种大于8/3的情况,这是由于球壳层的三维封闭结构;②当壳层结构ΔR→R1(圆球情况),对应几何因子参数均小于2,在壳层光学厚度很小时甚至出现e < 1.这是由于该情况下腔体的器壁曲率很大,而且形成球形封闭结构,对光子产生更大的束缚;③壳层的光学厚度非常小时(如ΔR=0.1对应的实线),介质对光子吸收的影响可以忽略,壳层的光输运通道完全“透明”,几何因子参数e完全由几何结构决定.
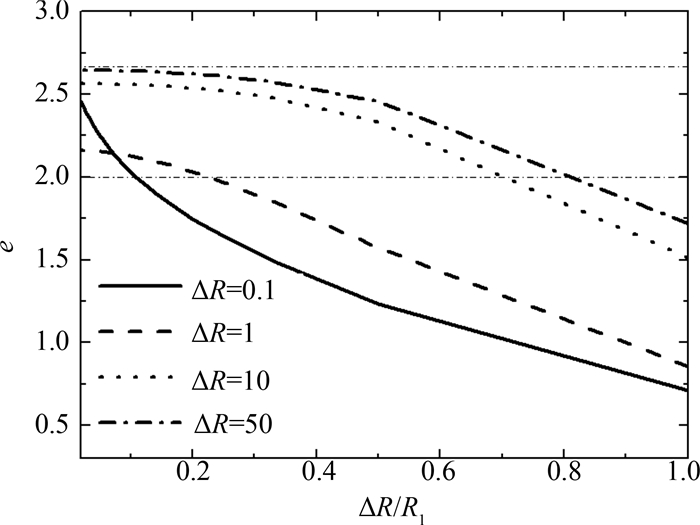 |
| 图 5 球壳层对应的几何因子会随着ΔR/R1的增大(内球半径的减小)而变小 Fig.5 Geometric factor decrees with ΔR/R1 |
几何自由程的计算公式(16)和(21)都非常复杂,需要进行繁琐的多重积分连续计算,而且需要足够细的积分区间划分才能保证精度.由于计算非常耗时,不便于辐射流体模拟程序直接使用.因此我们结合实际扩散(热传导)应用的需求,根据同心球壳层结构几何因子的数值计算结果,拟合出了便于调用的公式,
| $ {{\bar \eta }_{拟}} = \frac{{{a_1}\Delta R + {a_2}\Delta {R^2} + {a_3}\Delta {R^3}}}{{1 + {a_4}\Delta R + {a_5}\Delta {R^2} + {a_3}\Delta {R^3}}}. $ | (22) |
在0.2≤ΔR/R1≤0.4的范围内,可取a1=0.289 49+0.795 21ΔR/R1,a2=0.045 63+0.403 65ΔR/R1,a3=-0.022 95+0.157 55ΔR/R1,a4=0.463 85+0.741 75ΔR/R1,a5=0.036 57+0.502 75ΔR/R1,该拟合公式与公式(21)严格计算结果的误差在0.02%以内.在ΔR/R1 < 0.2和ΔR/R1 > 0.4时可使用同样的方法进行拟合,但相应拟合参数需要重新计算.
5 结论分析同心柱和同心球模型情况下,壳层输运介质中超声速扩散辐射波的几何自由程问题.得到两种模型辐射输运的能流和几何因子的计算公式,并通过数值求解给出几何因子ηe及几何因子参数e的数值结果,给出不同情况下几何因子的特性和修正方法.在ΔR=R1和R1
| [1] | LINDI J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J]. Phys Plasmas , 1995, 2 :3933–4024. doi:10.1063/1.871025 |
| [2] | ATZENI S, MEYER-TER-VEHN J. The physics of inertial fusion[M]. Oxford: Clarendon Press , 2003 : 204 -207. |
| [3] | MARSHAK R E. Effect of radiation on shock wave behavior[J]. Phys Fluids , 1958, 1 :24–32. doi:10.1063/1.1724332 |
| [4] | VESEY R A, HERRMANN M C, LEMKE R W, et al. Target design for high fusion yield with the double Z-pinch-driven hohlraum[J]. Phys Plasma , 2007, 14 :056302. doi:10.1063/1.2472364 |
| [5] | POMRANING G C. The equation of radiation hydrodynamics[M]. Oxford: Pergamon Press , 1973 . |
| [6] | ZELDOVICH Ya B, RAIZER, YU P. Physics of shock waves and high-temperature hydrodynamic phenomena[M]. New York: Dover Publications Inc , 1980 . |
| [7] | 李世昌. 高温辐射物理与量子辐射理论[M]. 北京: 国防工业出版社 , 1992 . |
| [8] | 于敏. 于敏论文集[M]. 北京: 北京应用物理与计算数学研究所 , 1996 . |
| [9] | 蓝可, 贺贤土, 赖东显, 李双贵. 柱输运管中扩散超声速辐射波的能流[J]. 物理学报 , 2006, 55 :3789–3795. |
 2016, Vol. 33
2016, Vol. 33

