| 第一性原理计算Cu-Cr共掺AlN稀磁半导体 |
氮化铝(AlN)是一种新型的III-V族直接带隙宽禁带[1]化合物半导体材料,在常温下是稳定的六方纤锌矿结构[2].在许多方面表现出非常独特的物理化学性能,具有广阔的应用前景.AlN 有良好的压电性质和较高的机电耦合系数,是GHz级声表面波装置的优选压电材料[3],此外 AlN 还具有无毒性,无环境污染和生产成本相对低廉等优点,是一种环保材料,在水和空气净化、消毒等方面也具有潜在应用价值[4-5],目前,对发展适用于器件的高质量n型和p型氮化铝晶体进行了深入研究,Ag具有电导率高,且为非磁性离子,在掺杂AlN中能得到光学质量较好的p型材料[6],研究者也已经成功完成了Si掺杂的AlN中的n型传导[4],具有很强的电导特性. 氮化铝晶体的n型掺杂问题已基本解决,但由于受到受主杂质的形成能高、电离能高以及易形成补偿效应等因素的影响,p型单掺氮化铝的空穴浓度极低.为实现高浓度空穴载流子以提高其导电性能,Reiss等人[7]提出了共掺杂理论,在克服宽禁带半导体的p型掺杂困难上引起了广泛关注,通过施主和受主有效地限制了本征缺陷的补偿效应,增强了p型受主的固溶度,降低了受主电离能并且改变载流子的迁移率,从而提高了p型传导率.
理想的DMS 应该在室温下具有铁磁性,而大量研究表明掺入磁性金属能得到高于室温的DMS[8-11].当采用磁性过渡金属掺杂AlN时,由于掺杂金属本身有磁性,它们的沉淀物以结团或者第二相的形式影响着铁磁性,因而在AlN 基的DMS 中,测量的平均磁矩要比预计的小得多,并且居里温度范围跨度也非常的大,这表明磁性杂质的贡献并不是一致的.Cui[12] 等计算表明,在GaN 基的DMS 中,Cr 的结团导致较低的平均磁矩.结团的 Cr 原子只存在反铁磁性的基态,因而降低总的磁矩,增强平均磁矩.同样的机理也可以用来解释以相似方法得到的AlN基的DMS.因而,在用磁性过渡金属掺杂AlN中,铁磁性的起源并不清楚.In杂质在GaAs 中是均匀的[13-14],表明用非磁性元素掺杂的方法可得到AlN 基DMS.因而,在用非磁性过渡族金属来代替磁性过渡族金属是可行的.这种杂质首先必须是没有磁性的,当掺杂以后,这些杂质应该和有限磁矩进行自旋极化,它们相互耦合产生铁磁性.Cu正是这样的杂质.第一性原理赝势计算法已经广泛应用于材料的性质研究[15-16],本文采用基于密度泛函理论的平面波赝势法(PWP)对Cu-Cr共掺杂AlN的32原子超原胞体系进行几何结构优化和性质计算,并对结果进行分析,研究掺杂体系的电子结构和光学性质.
1 模型结构与计算方法 1.1 模型构建理想的AlN多为六方纤锌矿结构,属于P63mc空间群,对称性为C6V-4,晶格参数为a=b=0.311 2 nm,c=0.498 2 nm,其中c/a为1.601[17].其晶胞由Al的六角密堆积与N的六角密堆积反向套构而成,比理想的六角密堆积结构的1.633小.计算基于超晶胞模型,取2×2×2(32原子)超晶胞体系,每个超晶胞包含16个Al原子和16个N原子.单掺时,由一个Cr原子替代体系中的一个Al原子实施掺杂,掺杂浓度为6.25%.Cu-Cr共掺AlN时在CuAl(Cu替换Al)原子固定下,分别对CrAlN(Cr替换Al)原子在1,2,3三种不同位置的情况下实现掺杂,超晶胞模型如图 1所示.
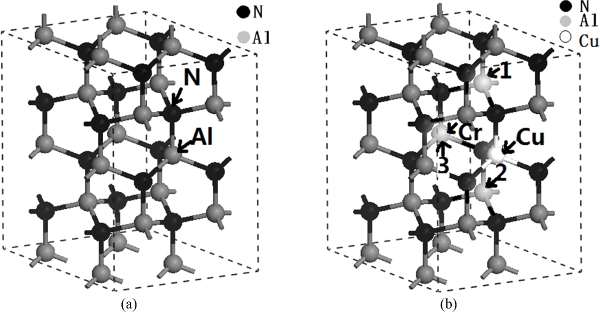 |
| 图 1 AlN和Cu-Cr共掺AlN 的32原子体系超晶胞结构图 Fig.1 Supercell structures of 32 atoms of AlN and Cu-Cr doped AlN |
计算由基于密度泛函理论(DFT)的量子力学程序[18]完成.计算中采用周期性边界条件,利用广义梯度近似(generalized gradient approximation,GGA)处理电子间的交换关联能.电子波函数采用平面波基超软赝势法[19]描述离子实与价电子间的相互作用,选取Al、N、Cu、Cr的价电子组态分别为Al: 3s23p1、 N: 2s22p3、 Cu: 3d104s1、 Cr: 3p63d54s1.在倒易的K空间中,所有的计算选取的平面波截断能(Ecut)为500 eV.体系总能和电荷密度在对布里渊(Brillouin)区的积分计算采用Monkhorst-Park[20]方案,对超晶胞体系选取K网格点为5×5×3,以保证体系能量和构型在准完备平面波基水平上的收敛,其自洽收敛精度为1.0×10-6 eV·atom-1.结构优化中采用BFGS[21]算法优化,其原子间相互作用力收敛标准设为0.01 eV,单原子能量收敛标准5.0×10-6 eV·atom-1,晶体内应力收敛标准为0.02 GPa,原子的最大位移收敛标准为5.0×10-5 nm.晶胞结构优化后,各项参数均优于收敛标准.
2 结果与讨论 2.1 纯AlN的电子结构由纯AlN计算所得,晶格参数a=b=0.311 2 nm,c=0.492 1 nm与实验值[22](a=b=0.311 2 nm,c=0.498 2 nm)相当接近,偏差仅为1.22%,说明本文的计算结果是可靠的.计算所得的带隙值为Eg=4.676 eV,比Miwa[23]等人的计算结果(4.09 eV)更接近实验值,但与实验值(6.2 eV)比较偏低,这是因为计算中采用的DFT为基态理论,而能系属于激发态,因此计算结果偏低.但不影响对AlN以及掺杂体系电子结构和性质的理论分析.图 2为AlN(2×2×2) 超原胞能带结构和态密度图.图中结果显示,AlN为直接带隙半导体.结合态密度可以看出,价带主要由N-2p态构成,而导带主要由Al-3p态构成,整体上表现出较明显的离子键性质.由总的态密度可以看出没有产生自旋劈裂现象,表明体系没有净磁矩.
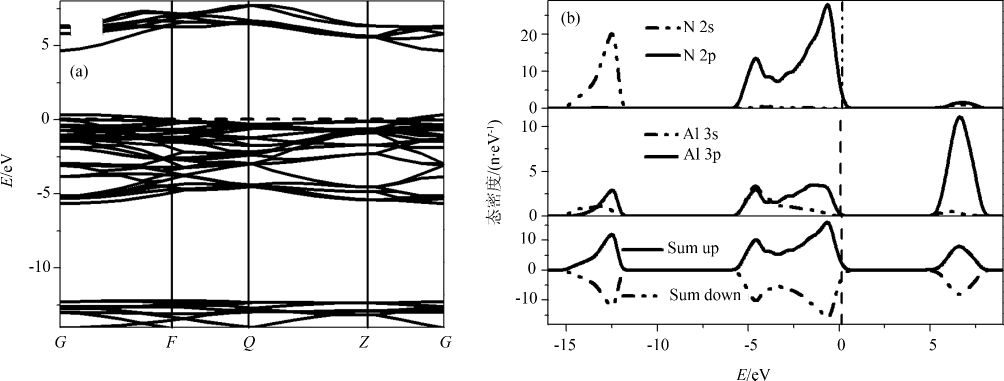 |
| 图 2 纯AlN(2×2×2) 超胞的能带结构图(a)和态密度图(b) Fig.2 Energy band structure (a) and DOS (b) of pure AlN (2×2×2) supercell |
已有研究表明[24-26]Cu掺杂AlN仍为直接带隙半导体,掺杂后体系带隙明显减小,费米能级贯穿于杂质带中,Cu的掺入在费米面上方引入了受主能级,因此,材料表现为半金属性. Cu-3d和N-2p电子的自旋向上和自旋向下的态密度发生劈裂,具有明显的铁磁性. 磁性的产生是通过Cu和相邻的N原子之间的p-d杂化作用来实现的.
图 3为Cr掺杂的AlN的自旋极化能带图. 由图可知,无论是自旋向上图 3(a)或自旋向下图 3(b)的能带图,导带底和价带顶位于Brillouin区的高对称点G点处,说明Cr掺杂AlN后的能带结构仍为直接带隙半导体,且都存在带隙,这表明Cr的掺杂未破坏AlN整体的半导体性质. 掺杂后在AlN 晶体的宽带隙中引入10条杂质带,其中5条自旋向上,5条自旋向下,杂质带宽为1.511 eV. 自旋向上的能带中,费米能级贯穿于杂质带,从而表现出一定的金属性. 而自旋向下的能带中,杂质带跨到费米能级上方,表现为半导体性质. 计算的带隙宽度达到4.214 eV,比上面计算的纯的AlN的带隙宽4.68 eV偏小. 因而,整体上掺杂体系呈现半金属性质. 半金属性的稳定性可以根据半金属带隙的大小判断,在能带图上可以看到半金属带隙为1.433 eV,这与樊玉勤[27]等人所计算的半金属带隙值相比偏大. Cr掺杂AlN有较稳定的半金属性,理论上可实现100%自旋极化载流的注入.
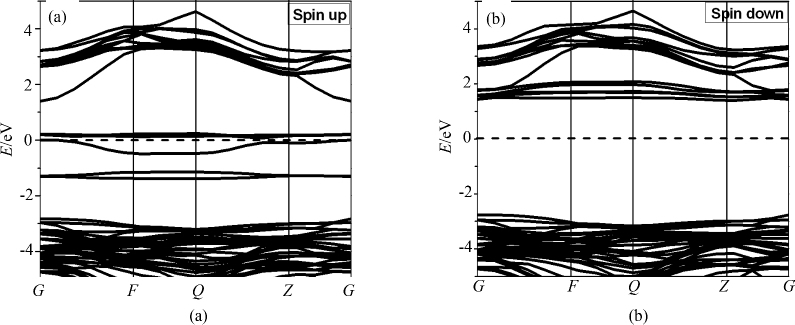 |
| 图 3 Cr单掺AlN的上自旋 (a)和下自旋 (b)的能带结构图 Fig.3 Spin polarized band structures of Cr doped AlN: (a) spin up,(b) spin down |
图 4为Cr掺杂AlN的自旋极化态密度图. 由于费米面附近的态密度分布决定着物质的铁磁性,因此主要讨论费米面附近的态密度. 从图 4可知,在费米面附近态密度出现了明显的劈裂现象,这表明体系中的电子通过相互交换作用出现了自旋有序排列. 自旋向上的电子跨过费米面,表现出金属性,自旋向下的电子在费米面处张开了一个较宽的带隙,表现出半导体性,这个结果和上面能带图的分析结果是一致的. 电子自旋向上与自旋向下的总态密度分布是不对称的,经对态密度积分计算可知,自旋向上的电子数多于自旋向下的电子数,体系的净磁矩为3.1 μB,主要是Cr的贡献,其余原子贡献微弱. 对比纯的AlN的分波态密度可知,最显著的变化来自于上价带与导带,上价带的峰值主要是Al-3s,3p、Cr-3d、N-2p电子构成,导带的峰值主要是Al-3p、Cr-3d电子构成.对于上自旋来说,Cr-3d和N-2p在0.1 eV几乎完全重叠耦合,出现非常强烈的杂化峰,显示了Cr和N之间的非常强烈的相互作用,即Cr-3d和N-2p发生杂化,结果表明Cr掺杂AlN的铁磁态是通过p-d杂化机理而存在的.
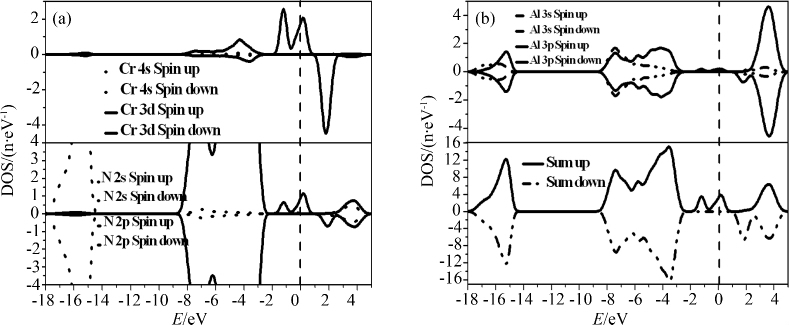 |
| 图 4 Cr单掺AlN的分波态密度图(a)和总的态密度图(b) Fig.4 DOS of Cr doped AlN: (a) partial DOS,(b) total DOS |
分别对纯AlN,Cr单掺AlN和Cu-Cr共掺AlN在Cu固定下,Cr在1,2,3不同掺杂位置的情况下进行计算.优化后的晶格常数和总能以及带隙值如表 1所示,可以看出,Cr单掺AlN和Cu与1,2,3不同位置的Cr共掺AlN的晶格常数a、b、c以及c/a,其计算结果都比纯AlN要大,主要是由于Cu,Cr原子的负电性较弱,AlN(Cr),Al(Cu-Cr)中无论是Cr3+还是Cu2+的半径都比Al3+的半径要大,这样Cr-N,Cu-N的键长都比Al-N的键长大,从而增大了晶格常数.对于Cu与1,2,3不同位置的Cr共掺AlN,由体系总能可以看出AlN(Cu-Cr)-3的这种掺杂位置优于其它两种掺杂位置.因此采用此结构的掺杂位置来分析AlN(Cu-Cr)-3的电子结构以及其光学性质.
| 表 1 纯AlN、Cr单掺和Cu-Cr共掺Al的晶格常数、总能和带隙值 Table 1 Lattice constant,total energy,and band gap of pure,Cr doped,and Cu-Cr co-doped AlN |
 |
| 点击放大 |
 |
| 图 5 Cu-Cr共掺AlN的上自旋 (a)和下自旋(b)的能带结构图 Fig.5 Band structures of Cu-Cr co-doped AlN: (a) spin up,(b) spin down |
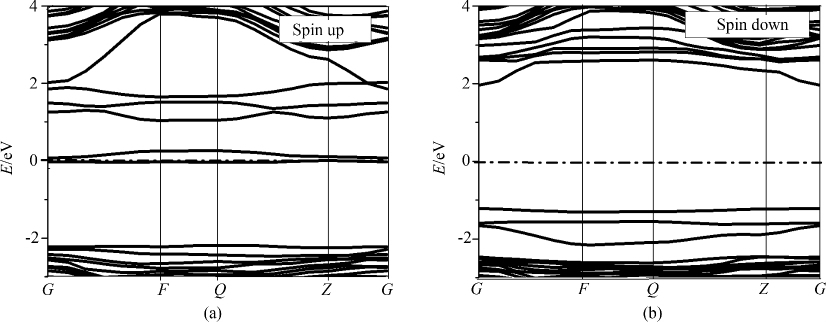
图 5为Cu-Cr共掺AlN的自旋极化能带图,由图可以看出:Cu-Cr共掺AlN后体系仍为直接带隙半导体,导带底和价带顶位于布里渊区的高对称点G点.无论是上自旋还是下自旋的能带图都存在带隙,这表明Cu-Cr原子的掺入并未破坏AlN整体的半导体性质.其下自旋带隙值为4.40 eV与Cr掺杂AlN的带隙值4.22 eV略大.但相比于纯AlN能带图的带隙值4.68 eV有所减小.从能带图中可知引入5条离散的未充满的杂质带,其中2条并入价带顶,杂质带位于带隙深处,杂质带宽度较Cr单掺时的0.25 eV增至1.89 eV,费米能级贯穿于这5条杂质带中,从而使Cu-Cr共掺体系整体表现出半金属性,且由于Cu原子的掺入增强了体系的金属性.这5条未充满的价带的作用像自由空穴一样,自旋向上态占据费米面,自旋向下未占据费米面,明显表现为自旋注入,即杂质带中可通过有效质量传输100%的自旋极化载荷子注入.该计算结果与Kim[28]采用第一性原理进行的能带计算结果类似.
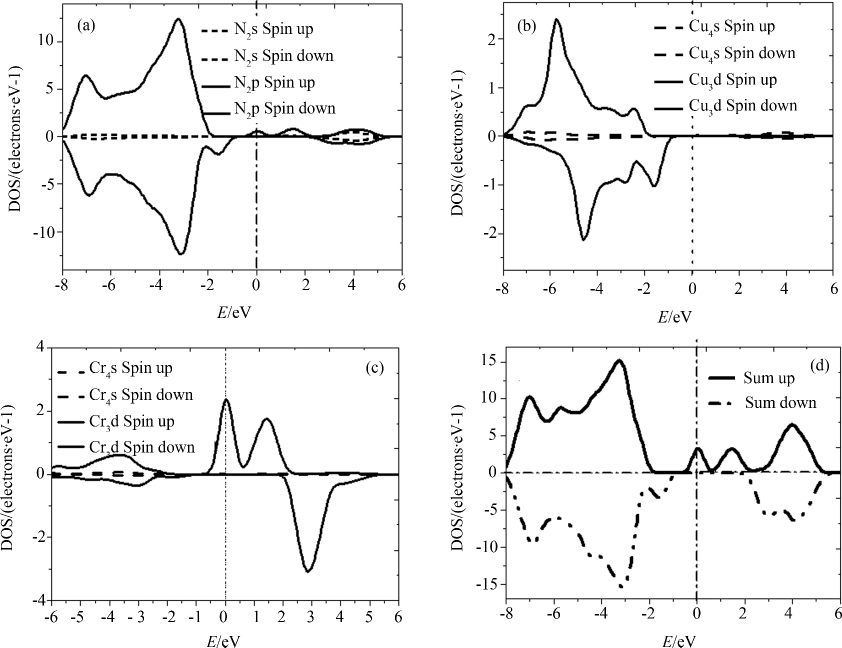
图 6为Cu、Cr、Al、N的分波态密度以及总的态密度,费米面附近的态密度分布决定着物质的磁性质,因此从总的态密度(d)以及结合图(a),(b),(c)可以看到,自旋向下的电子态密度在费米能级处张开一个能隙,说明Cu-Cr共掺并没改变AlN体系的半导体性质,而是引入自旋极化杂质带.自旋向上态中费米能级贯穿于Cu-3d杂质带中,自旋向下态中Cu-3d杂质带位于费米能级之上与导带底合并.说明Cu-Cr共掺杂体系仍具有半金属性,这与上面能带图的分析一致,在费米面附近,出现自旋向上和自旋向下的态密度分布劈裂,这表明体系中的电子通过交换相互作用出现了自旋有序排列.对费米能级以下的占据态进行态密度积分计算,自旋向上的电子数多于自旋向下的电子数,得出Cu-Cr共掺AlN后体系净磁矩为5.0 μB,其中Cr贡献3.16 μB,Cu贡献0.70 μB,Cu原子周围的四个N原子贡献为0.64 μB,其余N原子贡献甚微.因此对外表现净磁矩,其共掺杂后体系的净磁矩比Cr单掺AlN的增大,其贡献主要来源于Cu.因此,掺杂体系AlN(Cu-Cr)呈现铁磁性.
 |
| 图 6 Cu-Cr共掺AlN中N (a)、Cu (b)、Cr (c)的分波态密度及总的态密度(d) Fig.6 Partial DOS of (a) N,(b) Cu,(c) Cr and total DOS (d) of Cu-Cr co-doped AlN |
由Cu-Cr共掺杂的分波态图(a)、(b)、(c)可以看出,下价带的峰值主要来源于N-2s电子和Cu-4s电子,导带的峰值主要来源于Al-3p和Cu-4s电子,和Cr单掺AlN相比并没有发生变化,最显著的变化来源于上价带,上价带的峰值主要由Cr-3d和N-2p电子构成且二者形状极其相似,Cr-3d电子与N-2p电子在费米能级处峰值相对应,表明Cr-3d态电子和N-2p态电子发生强烈的p-d杂化效应,而Cu与N的相互作用相对较小.总体比Cr掺杂AlN的杂化效应要强.因此Cu-Cr和N的相互作用是铁磁态的,最近邻的N-2p电子更趋向与Cr-3d电子铁磁序排列. 由图 6(a)-(d)所示,费米能级进入价带顶,形成简并态,在费米能级附近引入了受主能级.掺杂使得AlN价带顶附近出现多余的载流子—空穴,而从由图 6(a)、(c)看出,自旋向上态中费米能级处出现Cu-Cr的3d态,使得费米能级处空穴密度增加,且杂质带加宽.
2.4 Cu-Cr共掺AlN的光学性质计算AlN掺杂前后的复折射率、介电函数、吸收谱、能量损失谱.根据半导体的光学性质,利用Kramers-Krönig关系,可以推导出晶体的介电函数的虚部、实部、吸收系数等[29].在线性响应范围内其宏观性质可以用复介电函数ε(ω)=ε1(ω)+iε2(ω)来描述,其中ε1(ω)=n2(ω)-k2(ω),ε2(ω)=2n(ω)k(ω),可以用ε1、 ε2描述晶体的光学性质,也可用n、 k来描述晶体的光学性质,二者是等价的.
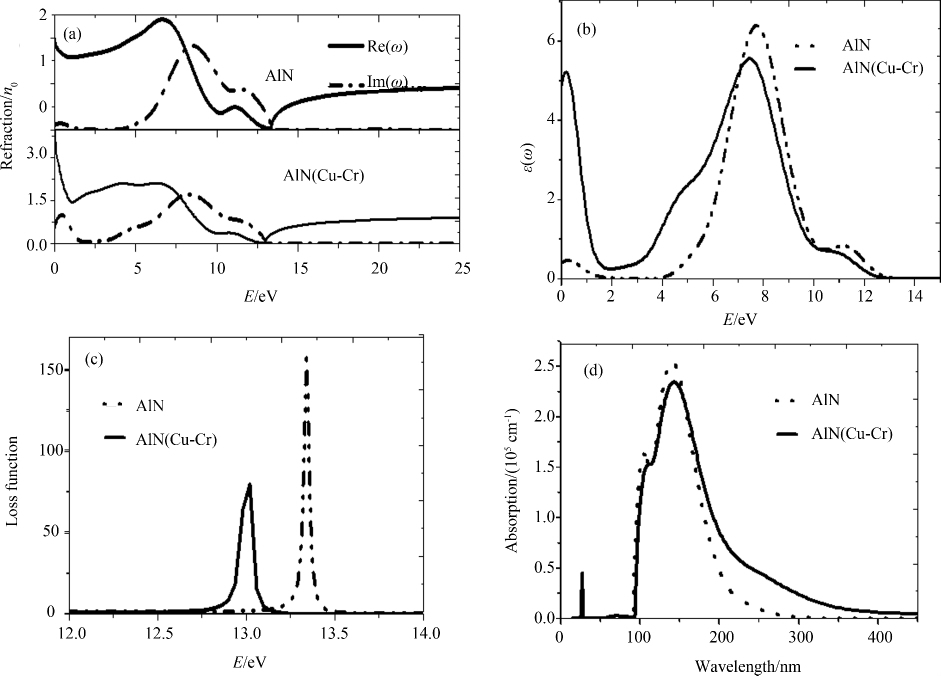
图 7为 Cu-Cr掺杂AlN的复折射率函数(a)、介电函数虚部(b)、AlN的能量损失谱(c)、吸收谱(d).由图 7(a)可知复折射率函数分别在AlN掺杂前后发生了明显的变化.可以看出,Cu-Cr共掺AlN后复折射率的实部和虚部都较纯AlN明显增大,即掺杂后吸收边发生了红移. 这和前面能带图中掺杂后带隙值变小相符合.图 7(b)为介电函数虚部,图中纯净的AlN的介电函数虚部有两个峰,其中峰1的能量为7.8 eV,峰2的能量11.3 eV,对应Cu-Cr共掺AlN后,在纯AlN 0-5.0 eV的原来没有峰的地方出现了两个峰,其中在0.3 eV的地方出现了一个更强的峰3,在能量为4.8 eV的地方出现了一个峰4,而Cu-Cr共掺AlN以后在0.3 eV的地方所出现的较强峰是由于Cr原子的3d态电子与N原子2p态电子发生强烈的杂化作用,且对应于纯AlN原来的两个峰(峰1和峰2) 向低能方向发生了偏移.介电函数虚部的图像明显变窄与能带图中带隙变窄相一致. 图 7(c)为能量损失谱,能量损失是描述电子在通过均匀的电介质时能量的损失情况的物理量,而能量损失峰则描绘等离子的共振频率[30].据该图可以看出,纯净AlN的损失峰位于13.4 eV左右,当Cu-Cr共掺AlN后,损失峰发生红移,向低能方向略有偏移对应着吸收谱的急剧下降,而Cu-Cr掺杂AlN后损失峰向低能方向偏移由纯AlN的大约13.4 eV移到位于12.9 eV的位置,且损失的能量较纯AlN减小约为纯AlN的1/2,图 7(d)为掺杂前后的光学吸收谱,可以得到吸收边换算到能量为4.0 eV左右,在200 nm以下吸收峰基本相符,但AlN(Cu-Cr)的吸收谱在25 nm左右的地方出现了一个尖锐的杂化峰,是由于Cr-3d电子与N-2p电子相互作用产生的,且可看出掺杂的吸收峰向长波方向延展,这也和掺杂后体系的带隙值变小,介电函数的吸收边发生红移相符合.
 |
| 图 7 Cu-Cr 共掺前后AlN的复折射率函数(a)、介电函数虚部(b)、能量损失谱(c)和吸收谱(d) Fig.7 Complex refractive index function (a),imaginary part of dielectric function (b),energy loss spectrum (c) and absorption spectrum (d) of AlN before and after Cu-Cr Co-doped |
采用基于密度泛函理论的总体能量平面波超软赝势方法,结合广义梯度近似(GGA),计算了Cr单掺AlN和Cu-Cr共掺AlN的晶格常数、能带结构、电子态密度以及体系的光学性质.结果表明,Cr单掺AlN以及Cu-Cr共掺AlN仍为直接带隙半导体,掺杂后体系带隙变窄,费米面附近引入深受主能级,体系表现出较稳定的半金属性;且Cu-Cr共掺杂AlN会产生强烈的自旋极化态,表明掺杂后材料引入了较强的铁磁性,掺杂后所得体系磁矩增大,通过对共掺杂后态密度的积分,可以看出磁性的产生其主要贡献来源于Cr,Cu原子以及与之相邻近的四个N原子.磁性的产生是通过Cu-Cr和与之相邻的N原子之间的p-d杂化来实现的.从而Cu-Cr共掺AlN可以获得铁磁性较好的稀磁半导体材料.通过对Cu-Cr共掺杂体系光学性质的分析表明,掺杂后,介电函数的吸收边发生红移,体系的吸收峰向长波方向延展,对长波的吸收加强,能量损失明显减小.
| [1] | LI J, NAM K B, NAKARMI M L, et al. Band structure and functional optical transition in wurtzile AlN[J]. Appl Phys Lett , 2003, 83 (25) :5163–5165. doi:10.1063/1.1633965 |
| [2] | YE H G, CHEN G D, ZHU Y Z, et al. First principle study of the native defects in hexagonal aluminum nitride[J]. Acta Phys Sin , 2007, 56 (9) :5376–5381. |
| [3] | LIU Y S, WANG L W, HUANG J P, et al. Growth of AlN thin film with ZnO buffer lawer[J]. Piezoelectrics & Acoustooptics , 2000, 22 (5) :322–325. |
| [4] | TANIYSU Y, KASU M, MAKIMOTO T. An aluminium nitride light-emitting diode with a wavelength of 210 nanometres[J]. Nature , 2006, 441 (7091) :325–328. doi:10.1038/nature04760 |
| [5] | DONG Y C, GUO Z Y, BI Y J, et al. First-principles calculation of AlN elecrtonic structure by doping with Zn and Cd[J]. Chinese J Lumin , 2009, 30 (3) :314–320. |
| [6] | DENG J Q, WU Z M, WANG A L, et al. First principle study of optical and electronic properties of Ag doped AlN semiconductors[J]. Chinese J Comput Phys , 2014, 31 (5) :618–624. |
| [7] | KOROTKOV R Y, GREGIE J M, WESSELS B W. Codoping of wide gap epitaxial 333-nitride semiconductors[J]. OptoElectron Rev , 2002, 10 (4) :243–248. |
| [8] | DIETL T, OHNO H, MATSUKURA F, et al. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors[J]. Science , 2000, 287 :1019–1022. doi:10.1126/science.287.5455.1019 |
| [9] | DIETL T, OHNO H, MATSUKURA F, et al. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors[J]. Phys Rev B , 2001, 63 :19–5205. |
| [10] | SATO K, KATAYAMA, YOSHIDA H. Material design for transparent ferromagnets with ZnO-based magnetic semiconductors[J]. Jpn J Appl Phys , 2000, 39 . |
| [11] | UEDA K, TABATA H, KAWAI T. Magnetic and electric properties of transition-metal-doped ZnO films[J]. Appl Phys Lett , 2001, 79 (7) :988–990. doi:10.1063/1.1384478 |
| [12] | CUI X Y, MEDVEDEVA J E, DELLEY B, et al. Role of embedded clustering in dilute magnetic semiconductors: Cr doped GaN[J]. Phys Rev Lett , 2005, 95 :256404–256407. doi:10.1103/PhysRevLett.95.256404 |
| [13] | CHO J H, ZHANG S B, ZUNGER A. Indium-indium pair correlation and surface ssegregation in InGaAs alloys[J]. Phys Rev Lett , 2000, 84 :3654. doi:10.1103/PhysRevLett.84.3654 |
| [14] | ZUNGER A, WOOD D M. Structural phenomena in coherent epitaxial solids[J]. Cryst Growth , 1989, 98 :1. doi:10.1016/0022-0248(89)90180-2 |
| [15] | LIU X K, ZHENG Z, LAN X H, et al. First-principles study of structure, elastic and thermodynamic properties of ZrV2[J]. Chinese J Comput Phys , 2013, 30 (2) :256–264. |
| [16] | PENG Q, YANG X X, DING J, et al. Thermodynamic properties of cubic KNO2 under atmospheric pressures: Density functional study[J]. Chinese J Comput Phys , 2013, 30 (2) :271–276. |
| [17] | ISHIHARA M, LI S J, YUMOTO H, et al. Characterization of cementite films prepared by electron-shower-assisted PVD method[J]. Thin Solid Films , 1998, 316 (1-2) :100–104. doi:10.1016/S0040-6090(98)00397-6 |
| [18] | SEGAL l M D, LINDAN P, PROBET M J, et al. First-principles simulation: ideas illustrations and the CASTEP code[J]. J Phys Condens Matter , 2007, 14 :2717. |
| [19] | VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Phys Rev B , 1990, 41 :7892. doi:10.1103/PhysRevB.41.7892 |
| [20] | MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations[J]. Phys Rev B , 1976, 13 :5188. doi:10.1103/PhysRevB.13.5188 |
| [21] | FISCHE T H, ALMLOF J A. General methods for geometry and wave function optimization[J]. J Phys Chem , 1992, 96 (24) :9768–9774. doi:10.1021/j100203a036 |
| [22] | ISHIHARA M, LI S J, YUMOTO H, et al. Control of preferential orientation of AlN films prepared by the reactive sputterang method[J]. Thin Solid Films , 1998, 316 (1) :152–157. |
| [23] | MIWA K, FUKUMOTO A. First-principles calculation of the structural, electronic and vibrational properties of gallium nitride and aluminum nitride[J]. Phys Rev B , 1993, 48 (11) :7897–7902. doi:10.1103/PhysRevB.48.7897 |
| [24] | VAN SCHILFGAARDE M, MYRASOV O N. Anomalous exchange interactions in III-V dilute magnetic semiconductors[J]. Phys Rev , 2001, B 63 :233205–233209. |
| [25] | KOROTKOV R Y, GREGIE J M, WESSELS B W. Optical properties of the deep Mn acceptor in GaN: Mn[J]. Appl Phys Lett , 2002, 80 :1731. doi:10.1063/1.1456544 |
| [26] | WEI J, PEIDE H, MEI C, et al. Electionic structure and ferro-magnetic properties of Cu-doped AlN from first principles[J]. J Appl Phys , 2007, 101 (11) :113918–113921. doi:10.1063/1.2745282 |
| [27] | FAN Y Q, WANG X Q, WANG L X, et al. First-principles study on electromagnetic properties of Cr doped AlN semiconductor[J]. Materials Review , 2009, 23 (z1) :082. |
| [28] | KIM J J, MAKINO H. MBE growth of GaMnN diluted magnetic semiconductors and its magnetic properties[J]. Materials Science in Semi Pro , 2003, 6 :503–506. doi:10.1016/j.mssp.2003.07.023 |
| [29] | SHEN X J. Semiconductor spectroscopy and optical properties[M].2nd ed. Beijing: Science , 2003 . |
| [30] | DUAN M Y, XU M, ZHOU H P, et al. First-principles study on the electronic structure and optical properties of ZnO doped with transition metal and N[J]. Acta Phys Sin , 2007, 56 (9) :5359–5365. |
 2016, Vol. 33
2016, Vol. 33


