| 液面冲击引起液滴飞溅问题的CIP方法数值模拟 |
2. 卫星海洋环境动力学国家重点实验室 国家海洋局第二海洋研究所 ;
3. 南京水利科学研究院水文水资源与水利工程科学国家重点实验室, 南京 210029
2. State Key Laboratory of Satellite Ocean Environment Dynamics Second Institute of Oceanography, SOA, China ;
3. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China
液滴飞溅是自然界中常见的现象,如:船舶航行砰击、水上飞机降落、空投鱼雷入水、垮塌桥梁落水等问题均涉及液滴飞溅现象.因此开展液滴飞溅的高精度数值模拟在科学研究和实际工程运用方面具有重要意义.该力学过程的难点在于自由液面破碎时的数值处理技术以及固液气交界面的相容性问题[1].而液滴冲击液面和物体入水问题是该问题的典型算例.
国内外学者通过理论分析、实验观测和数值模拟等方式对液滴飞溅问题进行了研究.Worthington[2]最早采用实验观测方法研究了液滴撞击液面的飞溅过程.Wagner[3]最早通过理论方法分析了固体冲击液面的过程.Bussmann等[4]开展了液滴冲击固壁面产生的飞溅现象的数值模拟.Duez等[5]通过实验方法研究了不同表面属性的球体入水引起的液滴飞溅特性.Minh和Gustav[6]开展了不同湿表面球体冲击水面引起的液滴飞溅现象的数值模拟.Eggers 等[7]开展了大冲击速度下的液滴冲击固壁面问题的分析研究.Shetabivashd等[8]开展了气体特性对液滴冲击薄膜问题影响的数值模拟研究.液滴冲击液面和固体冲击液面的问题蕴含着复杂多相流相互作用问题,作用时间非常短,涉及湍流和旋涡、物体的运动和变形、流固耦合作用等,并伴随着飞溅、融合等复杂自由面变形.受现有实验手段的限制,液滴飞溅过程中的一些细微问题,如液面内的速度场和压力场,难以测定.数值方法作为一种现代的研究手段,在流体运动模拟方面取得了极大成功,但对液滴飞溅过程的模拟还不够准确.
本文基于自主研发的CIP-ZJU[9-11]多相流数学模型,通过引入精度更高的自由面捕捉方法改进模型,开展不同物体冲击液面引起的液滴飞溅等问题的数值模拟.模型在直角坐标下建模,利用具有三阶精度的紧致插值曲线CIP方法作为流场的基本求解器,应用浸入边界方法处理流-固耦合作用问题,开展液滴冲击液面和柱体冲击液面问题的数值模拟,通过与文献结果的比较验证模型的精确性.
1 数学模型 1.1 控制方程不可压缩流体的固-液-气多相流控制方程:
| $\nabla \cdot u=0,$ | (1) |
| $\frac{\partial u}{\partial t}+(u\cdot \nabla )u=\frac{-1}{\rho }\nabla p+\frac{\mu }{\rho }{{\nabla }^{2}}u+F,$ | (2) |
| $\frac{\partial {{\phi }_{m}}}{\partial t}+u\cdot {{\nabla }_{m}}=0,$ | (3) |
其中,u为速度矢量,ρ为流体密度,p为压强,m为动力粘性系数,F为质量力,本文中质量力F等于重力加速度g. φm(m=1,2和3) 为流体的体积函数,表示流体在计算单元内占有体积的比值.网格内的流体特征λ(密度ρ或者动力粘性系数μ)通过下式得到:
| $\lambda =\sum\limits_{m=1}^{2}{{{\phi }_{m}}{{\lambda }_{m}}}.$ | (4) |
模型采用分步解法求解Navier-Stokes方程.首先使用CIP方法求解对流项,再采用中心差分方法求解扩散项,然后进行压力-速度耦合计算,完成速度场和压力场的求解,最后进行自由面重构[9].
1) 对流项(I)
| $\begin{align} & \frac{\partial u}{\partial t}+(u\cdot \nabla )u=0, \\ & \frac{\partial ({{\partial }_{i}}u)}{\partial t}+(u\cdot \nabla )({{\partial }_{i}}u)=0. \\ \end{align}$ | (5) |
通过CIP方程可得到方程的解
| $\begin{align} & {{u}^{*}}=X(x-u\Delta t), \\ & {{({{\partial }_{i}}u)}^{*}}\left( x \right)=\frac{\partial {{X}^{*}}}{\partial {{x}_{i}}}(x-u\Delta t). \\ \end{align}$ | (6) |
式中:X为待确定系数函数,*为对流项计算结束后的时间标志[13].
2) 非对流项(I)
下面进行扩散项的计算
| $\begin{align} & \frac{\partial u}{\partial t}=\frac{\mu }{\rho }{{\nabla }^{2}}u+F, \\ & \frac{\partial ({{\partial }_{i}}u)}{\partial t}=-{{\partial }_{i}}u\cdot \nabla u+{{\partial }_{i}}\left( \frac{\mu }{\rho }{{\nabla }^{2}}u+F \right). \\ \end{align}$ | (7) |
扩散项的时间离散采用显示格式,中间速度可表示为
| $\begin{align} & \frac{{{u}^{**}}-u}{\Delta t}=\frac{\mu }{\rho }{{\nabla }^{2}}u+F, \\ & \frac{{{({{\partial }_{i}}u)}^{**}}-{{({{\partial }_{i}}u)}^{*}}}{\Delta t}=-{{\partial }_{i}}{{u}^{*}}\cdot \nabla {{u}^{*}}+{{\partial }_{i}}\left( \frac{\mu }{\rho }{{\nabla }^{2}}{{u}^{*}}+F \right), \\ \end{align}$ | (8) |
其中方程(8) 的空间离散采用中心差分格式.
3) 非对流项(II)
然后进行压力和速度匹配的计算.
| $\begin{align} & \frac{\partial u}{\partial t}=-\frac{1}{\rho }\nabla p, \\ & \frac{\partial ({{\partial }_{i}}u)}{\partial t}=-{{\partial }_{i}}\left( \frac{1}{\rho }\nabla p \right). \\ \end{align}$ | (9) |
通过对方程(9) 取散度,并引入连续方程,可得到如下形式的泊松方程
| $\nabla \cdot \left( \frac{1}{\rho }\nabla {{p}^{n+1}} \right)=\frac{1}{\Delta t}\nabla \cdot {{u}^{**}},$ | (10) |
泊松方程的求解通过SOR迭代得到.
考虑动量方程的压力梯度项,计算速度的最终值,计算式为
| $\begin{align} & {{u}^{n+1}}={{u}^{**}}-\frac{\Delta t}{\rho }\nabla {{p}^{n+1}}, \\ & {{({{\partial }_{i}}u)}^{n+1}}={{({{\partial }_{i}}u)}^{**}}-\Delta t{{\partial }_{i}}\left( \frac{1}{\rho }\nabla {{p}^{n+1}} \right). \\ \end{align}$ | (11) |
根据式(3) 和(4) 进行自由面的更新和网格内流体信息,然后返回到步骤1) ,这样就完成了整个计算过程,一直到设定的步骤结束[9-10].
1.3 CIP方法CIP 方法是Takewaki(1985) [14]等人于20世纪80年代中期提出并发展起来,用于求解双曲型偏微分方程的计算方法.为了更好地解释CIP方法,我们考虑简单的常系数一维对流方程
| $\frac{\partial f}{\partial t}+u\frac{\partial f}{\partial x}=0,$ | (12) |
其中u为大于零的常数.此类偏微分方程可用不同差分方法求解.下面将给出CIP方法的工作原理.图 1(a)-(c)给出了一阶迎风差分方法的工作原理,对于一阶差分格式来说,它利用直线的方式联立相邻两个节点的信息来工作,而忽略了网格内部的信息,导致较大的数值耗散.为了真实再现网格内部的信息,我们有必要求助高阶差分方法,而对于常规高阶差分的建立需要更多的网格点的信息.CIP采用一种独特的方式,在一个网格内实现了高阶差分格式,通过利用空间网格点的变量值及其空间导数值,来描述该网格内的信息,可真实再现网格内的信息.
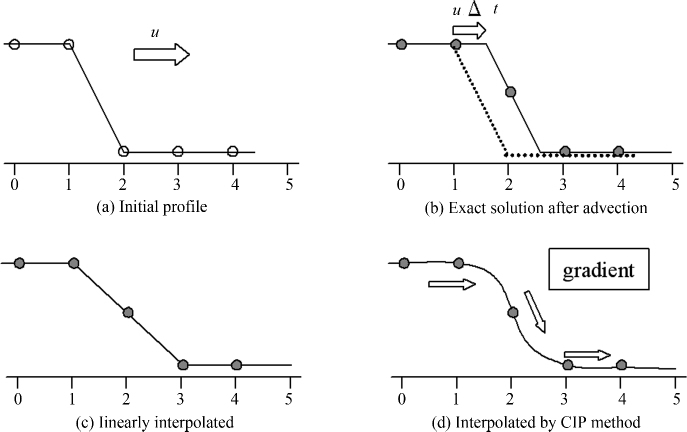 |
| 图 1 CIP方法的基本原理图 Fig.1 Principle of CIP method |
通过对方程(12) 求关于x的偏导,我们得到如下的空间导数方程
| $\frac{\partial g}{\partial t}+u\frac{\partial g}{\partial x}=-g\frac{\partial u}{\partial x}.$ | (13) |
其中g=∂f/∂x.因对流速度u为常数,方程(13) 右边项为0.这样,方程(13) 与方程(12) 有相同的形式.对于u>0的情况,在迎风向网格单元[xi-1,xi]内n时刻的剖面函数fn可以近似为
| ${{F}_{i}}^{n}\left( x \right)={{a}_{i}}{{(x-{{x}_{i}})}^{3}}+{{b}_{i}}{{(x-{{x}_{i}})}^{2}}+{{c}_{i}}(x-{{x}_{i}})+{{d}_{i}}.$ | (14) |
在n+1时刻的单元格剖面函数量fn+1可以通过将n时刻的剖面函数fn平移-uΔt得到,函数f和g的时间演变可以通过下面的拉格朗日变换得到
| ${{f}_{i}}^{n+1}={{F}_{i}}^{n}({{x}_{i}}-u\Delta t),{{g}_{i}}^{n+1}=d{{F}_{i}}^{n}({{x}_{i}}-u\Delta t)/dx.$ | (15) |
因此,从CIP对流格式采用了拉格朗日常量解法(Lagrangian invariant solution)的角度来看,CIP对流格式又称为半拉格朗日方法,如图 2所示.公式(14) 中的四个未知系数可由已知量fin,fi-1n,gin和gi-1n通过下列关系式来确定:
| $\begin{align} & {{a}_{i}}=\frac{{{g}_{i}}^{n}+{{g}_{i-1}}^{n}}{\Delta {{x}^{2}}}-\frac{2({{f}_{i}}^{n}-{{f}_{i-1}}^{n})}{\Delta {{x}^{3}}},\text{ }{{c}_{i}}={{g}_{i}}^{n}, \\ & {{b}_{i}}=\frac{2{{g}_{i}}^{n}+{{g}_{i-1}}^{n}}{\Delta x}-\frac{3({{f}_{i}}^{n}-{{f}_{i-1}}^{n})}{\Delta {{x}^{2}}},\text{ }{{d}_{i}}={{f}_{i}}^{n}. \\ \end{align}$ | (16) |
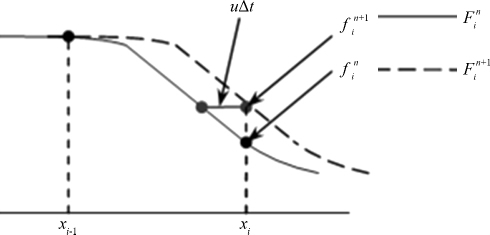 |
| 图 2 半拉格朗日方法的CIP格式 Fig.2 CIP method as a kind of semi-Lagrangian method |
CIP方法采用一种独特的方式,在一个网格内实现了高阶差分格式,使得本文的数值模型可以应用于复杂流动问题的模拟,这也是本文所采用的差分方法与其它方法的不同之处.利用上述思想两节点之间建立三次曲线方程的思想,CIP方法可进一步拓展到二维问题,利用四节点信息建立三次曲面方程[12].
对于网格节点(i,j),它迎风向周围的四个网格节点分别为(i,j),(iw,j),(i,jw),(iw,jw),其中iw=i-sign(u),jw=j-sign(v).n时刻节点(i,j)迎风方向网格单元内对应的三次曲面方程的表达式如下:
| $\begin{align} & X\left( \xi ,\eta \right)={{C}_{30}}{{\xi }^{3}}+{{C}_{21}}{{\xi }^{2}}\eta +{{C}_{12}}\xi {{\eta }^{2}}+{{C}_{03}}{{\eta }^{3}} \\ & +{{C}_{20}}{{\xi }^{2}}+{{C}_{11}}\xi \eta +{{C}_{02}}{{\eta }^{2}}+{{C}_{10}}\xi +{{C}_{01}}\eta +{{C}_{00}}, \\ \end{align}$ | (17) |
其中,
| $\begin{align} & {{C}_{30}}=\{\xi \left[ {{\chi }_{x}}^{n}\left( iw,j \right)+{{\chi }_{x}}^{n}\left( i,j \right) \right]- \\ & 2\left[ {{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,j \right) \right]\}/{{\xi }^{3}}, \\ & {{C}_{03}}=\{\eta \left[ {{\chi }_{y}}^{n}\left( i,jw \right)+{{\chi }_{y}}^{n}\left( i,j \right) \right]- \\ & 2\left[ {{\chi }^{n}}\left( i,jw \right)-{{\chi }^{n}}\left( i,j \right) \right]\}/{{\eta }^{3}}, \\ & {{C}_{20}}=\{-\xi \left[ {{\chi }_{x}}^{n}\left( iw,j \right)+2{{\chi }_{x}}^{n}\left( i,j \right) \right]+ \\ & 3\left[ {{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,j \right) \right]\}/{{\xi }^{2}}, \\ & {{C}_{21}}=\{[{{\chi }^{n}}\left( iw,jw \right)-{{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,jw \right) \\ & +{{\chi }^{n}}\left( i,j \right)\left] -\xi \right[{{\chi }_{x}}^{n}\left( i,jw \right)-{{\chi }_{x}}^{n}\left( i,j \right)]\}/({{\xi }^{2}}\eta ), \\ & {{C}_{12}}=\{[{{\chi }^{n}}\left( iw,jw \right)-{{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,jw \right) \\ & +{{\chi }^{n}}\left( i,j \right)\left] -\eta \right[{{\chi }_{y}}^{n}\left( iw,j \right)-{{\chi }_{y}}^{n}\left( i,j \right)]\}/(\xi {{\eta }^{2}}), \\ & {{C}_{11}}=-[{{\chi }^{n}}\left( iw,jw \right)-{{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,jw \right) \\ & +{{\chi }^{n}}\left( i,j \right)\left] /\left( \xi \eta \right)+\{\xi \right[{{\chi }_{x}}^{n}\left( i,jw \right)-{{\chi }_{x}}^{n}\left( i,j \right)]+ \\ & {{\eta }_{1}}\left[ {{\chi }_{y}}^{n}\left( iw,j \right)-{{\chi }_{y}}^{n}\left( i,j \right) \right]\}/\left( \xi \eta \right)= \\ & \left[ {{\chi }^{n}}\left( iw,jw \right)-{{\chi }^{n}}\left( iw,j \right)-{{\chi }^{n}}\left( i,jw \right)+{{\chi }^{n}}\left( i,j \right) \right] \\ & /\left( \xi \eta \right)-{{C}_{21}}\xi -{{C}_{12}}\eta , \\ & {{C}_{10}}={{\chi }_{x}}^{n}\left( i,j \right), \\ & {{C}_{01}}={{\chi }_{y}}^{n}\left( i,j \right), \\ & {{C}_{00}}={{\chi }^{n}}\left( i,j \right), \\ & \xi =-sign(u\Delta t), \\ & \eta =-sign(v\Delta t). \\ \end{align}$ | (18) |
根据公式(18) 确定插值多项式的系数后,即可采用类似于一维情形中的拉格朗日变换得到n+1时刻(i,j)节点迎风方向网格单元剖面函数值.
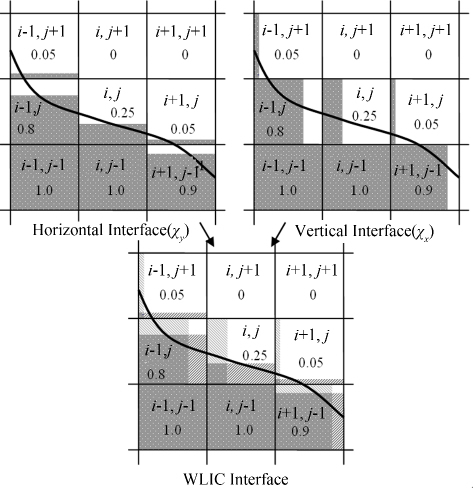
1.4 自由面捕捉CIP方法不但可求解动量方程的对流项,同时还可用来重构自由面.由于CIP方法本身没有质量守恒条件,在多相流计算中使用CIP方法进行自由面重构容易产生液面的“钝化”现象,因此需要选用具有质量守恒条件的VOF类型方法进行自由面重构.本文的自由面捕捉方式采用平衡格式的VOF方法(VOF/WLIC方法),该方法由Yokoi[15]在Hirt[16]等提出的传统VOF方法的基础上改进得到,其在每次计算中对每个方向的流量作加权平均得到修正的流量,在保证其算法易用、高效的前提下进一步提高了计算精度.该方法既保持了传统VOF质量守恒和较易实施的特点,又可得到紧致自由面.其工作原理如图 3所示,采用此方法可实现自由面的高精度重构.
1.5 流固耦合处理采用浸入边界 (Immersed Boundary Method)[17]方法处理流-固耦合作用问题.
| $~{{u}^{n+1}}={{\phi }_{3}}{{U}_{b}}^{n+1}+(1-{{\phi }_{3}}){{u}_{f}}^{n+1},$ | (19) |
其中ufn+1为在欧拉坐标体系中通过式(11) 计算得到的“局部”流场速度; Ubn+1是通过拉格朗日方法得到的固体的运动速度[12]; un+1为二者耦合作用的“整体”速度,这样就得到了流-固耦合速度场;该时刻速度场作为下一时刻的初始条件,进入下一步的流场求解.该方法也可称为固体体积流-固耦合处理方法.基于浸入边界方法的流-固耦合技术,采用固定网格,在计算过程中无需更新网格,可保证模型的高效率,使得模型在处理大位移的流-固耦合计算中具有强大优越性.本文采用的方法具有较易实施的优势,方便模型向三维拓展.
2 数值计算结果及分析下面利用上述建立的模型开展液滴飞溅问题的数值模拟.
2.1 液滴冲击液膜问题液滴冲击液膜的初始状态如图 4所示.液滴半径r=2 mm,液膜高度h=0.6 mm,初始时刻液滴与水膜相切,液滴冲击速度v=1.0 m·s-1,方向垂直向下.液滴和液膜均采用水作为液相,密度为1.0×103 kg·m-3,粘度为1.25×10-3 Pa·s;空气密度取1.25 kg·m-3,粘度取1.0×10-5 Pa·s.计算区域大小为10 mm×10 mm,采用200×200的均匀网格,计算时间步长为10-6 s.
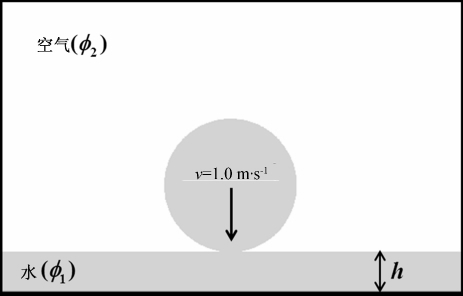 |
| 图 4 液滴冲击自由面示意图 Fig.4 Schematic of drop impact onto a surface |
图 5给出t=0.001 8秒时刻采用不同自由面捕捉方法模拟结果,分别采用CIP、VOF和VOF/WLIC三种自由面捕捉方法模拟了该问题.图中选用f=0.05、0.5和0.95三条等值线表示自由面.图 5(a)为CIP方法作为自由面捕捉方法模拟的结果,可看出自由面紧致性较差,无明显的液滴断裂、分离的现象,若采用f=0.5作为等值线,则无法观察到水体断裂信息;图 5(b)为传统的VOF方法的模拟结果,可看出水体飞溅现象较明显,但是断裂后的水体“碎屑”现象较严重,与实际情况不符;如图 5(c)所示,采用VOF/WLIC方法可得到较紧致的自由面,且可观察到明显的液滴分离现象,无“碎屑”出现.结果表明VOF/WLIC方法更适用于液滴冲击过程中的自由面重构,下面的模拟工况都将采用VOF/WLIC方法重构自由面.
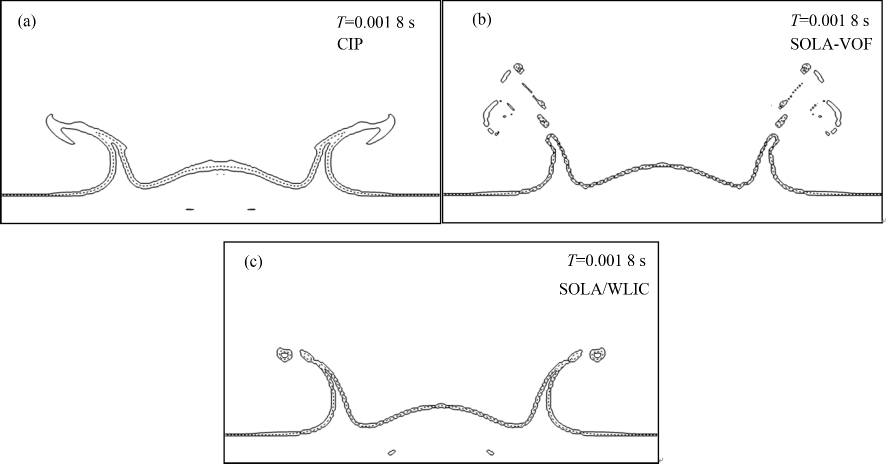 |
| 图 5 不同自由面捕捉方式比较 Fig.5 Simulated water surface using different surface capturing methods |
下面模拟圆柱对水面冲击引起的液面大变形问题.模型设置如图 6所示,圆柱半径R为0.055 m,圆柱中心距离水面的距离为0.5 m,圆柱做自由落体运动,圆柱的密度与水的密度一样.本模拟中,圆柱在液面上方0.1 m处以试验中的圆柱接触液面的入水速度冲击液面.计算中分别采用了三套网格,网格1 (120×111) 、网格2 (168×152) 和网格3 (260×265) ,最小网格大小分别为0.01 m、0.005 m和0.002 m.
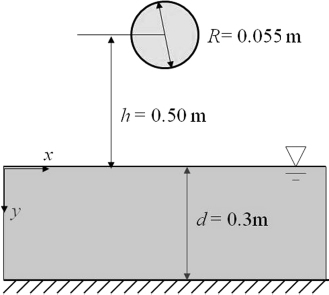 |
| 图 6 圆柱体冲击液面示意图 Fig.6 Schematic configuration of a cylinder impact onto a surface |
图 7给出了圆柱入水深度与Greenhow & Lin (1983) [18]试验结果的比较.可观察到模拟结果与实验结果相比有一定的时间滞后,而三套网格的差异性较小,细网格的结果更接近实验结果.图 8和9分别给出了三套网格条件下圆柱的运动速度和入水过程中圆柱所承受的竖向力.从图中可观察到网格1由于网格尺寸较大,入水时刻滞后;而网格2和3具有较好的一致性,说明网格2和3已完全收敛.
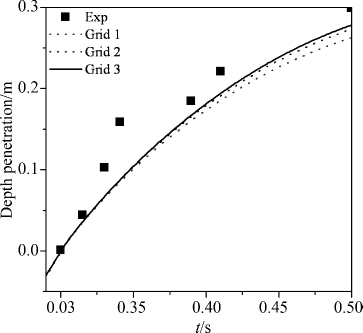 |
| 图 7 圆柱入水深度与实验结果[18]的比较 Fig.7 Comparison of penetration depth of simulation and experimental data[18] |
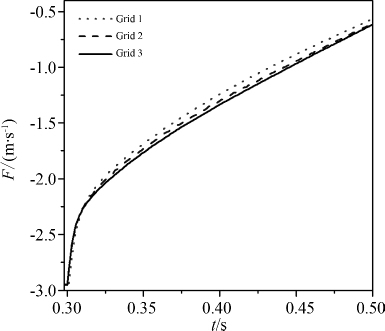 |
| 图 8 计算网格对圆柱入水速度的影响 Fig.8 Effect of grid resolution on penetration velocity |
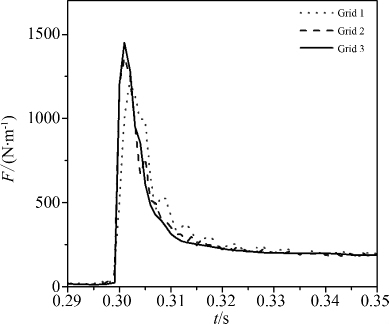 |
| 图 9 计算网格圆柱入水过程中受力的影响 Fig.9 Effect of grid resolution on cylinder impact force |
图 10给出了t=0.315s和t=0.5s时刻,三套网格模拟得到的液面形状与实验结果的比较,可看出二者具有较好的一致性,圆柱入水过程中的波浪破碎、液滴飞溅等现象可有效捕捉,同时细网格能更真实重现圆柱冲击液面过程中液面大变形问题.
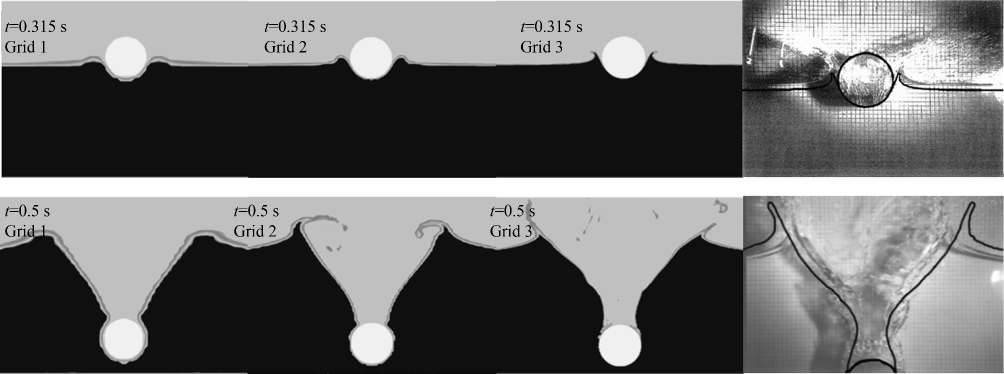 |
| 图 10 不同网格模拟得到的液面与实验结果[18]的比较 Fig.10 Comparison of surface profile between simulations and experimental data[18] |
下面开展不同密度的柱体冲击液面问题的数值模拟.初始设置和图 6一样,只是此时圆柱的密度为水体密度的一半,其它条件可参考上面的算例.图 11给出了圆柱入水深度与实验结果的比较,可发现二者具有较好的一致性.由于圆柱的密度小于水的密度,当圆柱到达一定深度后开始上升,模拟得到的圆柱下沉的最大深度发生在t=0.5 s处.图 12和13分别给出了不同网格下圆柱运动速度和圆柱入水过程中承受的竖向力,趋势和上面的算例图 8和图 9基本一致,入水速度受网格大小的影响较小,初始入水阶段圆柱的速度快速降低;砰击力的峰值出现在柱体初始入水时刻.
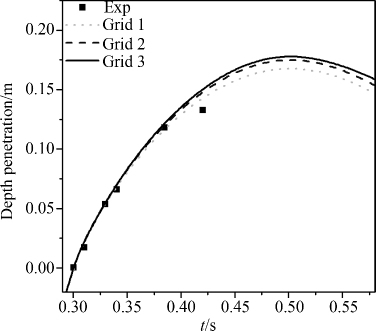 |
| 图 11 圆柱入水深度与实验结果[18]的比较 Fig.11 Comparison of penetration depth of simulation and experimental data[18] |
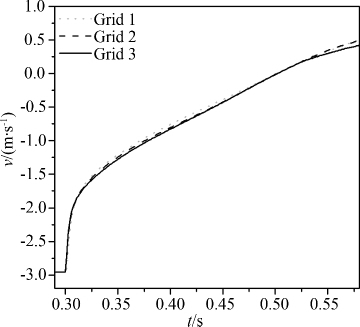 |
| 图 12 计算网格对圆柱入水速度的影响 Fig.12 Effect of grid resolution on penetration velocity |
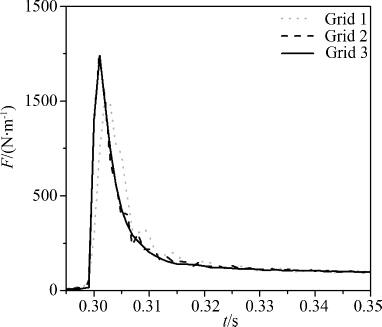 |
| 图 13 计算网格圆柱入水过程中受力的影响 Fig.13 Effect of grid resolution on cylinder impact force |
图 14给出了不同时刻圆柱位置与实验结果的比较,可知本文的模拟结果与实验结果具有高度一致性.t=0.305 s时刻,柱体初始接触水面,柱体受到剧烈的冲击力作用.柱体的初始速度会“挤”开液面(t=0.320 s),随着圆柱入水深度的增大,“挤”开的水体也在增多,会向上方和两边运动(t=0.330 s);随着圆柱入水深度的进一步增大,被圆柱“挤”开的水体由于周围水体的“压迫”的影响,有恢复“原位”的趋势(t=0.385 s).
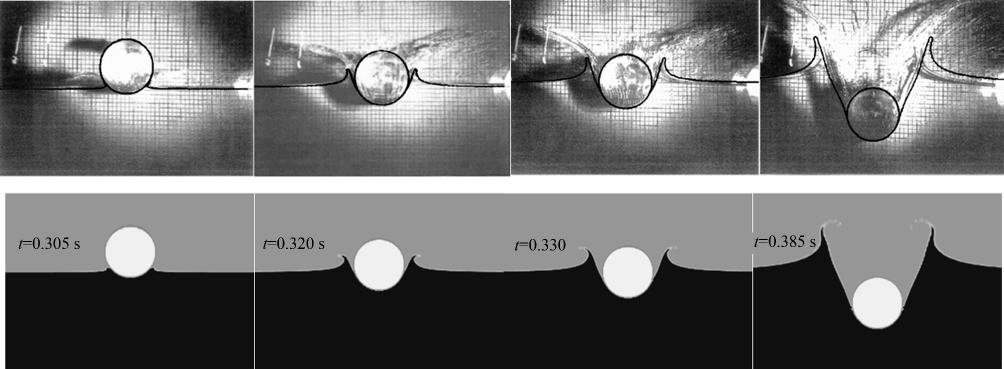 |
| 图 14 不同时刻圆柱位置与实验结果[18]的比较 Fig.14 Comparison of instant cylinder position between simulation and experimental data[18] |
下面综合分析不同质量柱体入水过程中的水动力特性.计算条件如图 6所示,采用网格2 (168×152) 开展了数值模拟.分别选用三种柱体密度: ρ柱=0.5ρ水、 0.5ρ水和1.5ρ水.图 15-17分别给出了不同质量圆柱的入水深度、入水速度和冲击压力.从图中可知同时刻,质量较小圆柱的入水深度较小、且随着时间推移入水深度变化较缓慢;而质量较大圆柱的入水深度快速增长,说明重力是圆柱运动的主要驱动力.在初始入水时刻,圆柱会受到瞬时砰击力,如图 16所示,砰击力瞬时增大到峰值,然后慢慢降低到稳定的状体;由于瞬时砰击力的作用,圆柱的运动速度快速降低,然后达到相对平衡的状态,速度稳定降低(图 15).而由于1.5ρ水的柱体主要受重力的作用,水动力的影响较小,柱体很快达到槽底,速度迅速降为零.
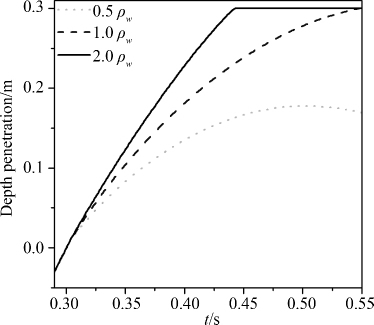 |
| 图 15 圆柱质量对入水深度的影响 Fig.15 Effect of cylinder mass on penetrationdepth |
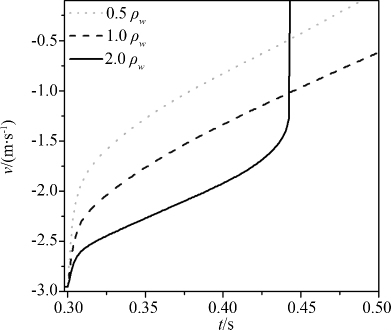 |
| 图 16 圆柱质量对入水速度的影响 Fig.16 Effect of cylinder mass on penetrationvelocity |
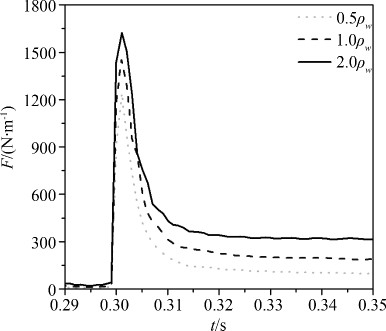 |
| 图 17 圆柱质量对冲击力的影响 Fig.17 Effect of cylinder mass on impact force |
基于自主研发的CIP-ZJU数学模型,开展了不同物体冲击液面引起的液滴飞溅等自由面大变形问题的数值模拟.采用高阶差分CIP方法离散了Navier-Stokes方程,利用VOF/WLIC方法改进了原数学模型,更加精确地重构了自由面,通过浸入边界的方法处理了流-固耦合问题.开展了液滴冲击液面、柱体冲击液面等问题的数值模拟,并通过与文献结果的比较验证了模型的有效性;首先通过开展液滴冲击液面的模拟,验证了VOF/WLIC方法重构自由面大变形问题能力;然后模拟了柱体入水问题,验证了CIP-ZJU模型模拟固-液-气多相流耦合作用问题;研究发现入水初期柱体会受到瞬时砰击力作用,运动速度迅速降低,柱体完全进入水中后,运动较稳定.结果表明本文的模型可有效处理自由面大变形流动问题,流场特性的研究将是下一步工作的重点.
| [1] | SUN S L, SUN Y L, HU J Z, HU J. Free surface effect and spike of a cylinder piercing water surface[J]. Chinese Journal of Computational Physics , 2013, 30 (2) :187–193. |
| [2] | WORTHINGTON A M. On the forms assumed by drops of liquids falling vertically on a horizontal plate[J]. Proc R Soc Lond , 1876, 25 (171-178) :261–272. doi:10.1098/rspl.1876.0048 |
| [3] | WAGNER H. Phenomena associated with impacts and sliding on liquid surfaces[J]. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschriftfür Angewandte Mathematik und Mechanik , 1932 (12) :193–215. |
| [4] | BUSSMANN M, CHANDRA S, MOSTAGHIMI J. Modeling the splash of a droplet impacting a solid surface[J]. Physics of Fluids , 2000, 12 (12) :3121–3132. doi:10.1063/1.1321258 |
| [5] | DUEZ C, YBERT C, CLANET C, BOCQUET L. Making a splash with water repellency[J]. Nature Physics , 2007 (3) :180–183. |
| [6] | MINH DO-QUANG, GUSTAV AMBERG. The splash of a solid sphere impacting on a liquid surface: Numerical simulation of the influence of wetting[J]. Physics of Fluids , 2009, 21 :022102. doi:10.1063/1.3073968 |
| [7] | EGGERS J, FONTELOS M A, JOSSERAND C, ZALESKI S. Drop dynamics after impact on a solid wall: Theory and simulations[J]. Physics of Fluids , 2010, 22 :062101. doi:10.1063/1.3432498 |
| [8] | SHETABIVASH H, OMMI F, HEIDARINEJAD G. Numerical analysis of droplet impact onto liquid film[J]. Physics of Fluids , 2014, 26 :012102. doi:10.1063/1.4861761 |
| [9] | ZHAO X Z, HU C H. Numerical and experimental study on a 2-D floating body under extreme wave conditions[J]. Applied Ocean Research , 2012, 35 (1) :1–13. |
| [10] | ZHAO X Z, YE Z T, FU Y N, CAO F F. A CIP-based numerical simulation of freak wave impact on a floating body[J]. Ocean Engineering , 2014, 87 :50–63. doi:10.1016/j.oceaneng.2014.05.009 |
| [11] | ZHAO X Z, YE Z T, FU Y N. Green water loading on a floating structure with degree of freedom effects[J]. Journal of Marine Science and Technology , 2014, 19 :302–313. doi:10.1007/s00773-013-0249-7 |
| [12] | HU C H, KASHIWAGI M. A CIP-based method for numerical simulations of violent free surface flows[J]. Journal of Marine Science and Technology , 2004, 9 :143–157. doi:10.1007/s00773-004-0180-z |
| [13] | YABE T, XIAO F, UTSUMI T. The constrained interpolation profile method for multiphase analysis[J]. Journal of Computational Physics , 2001, 169 (2) :556–593. doi:10.1006/jcph.2000.6625 |
| [14] | TAKEWAKI H, NISHIGUCHI A, YABE T. Cubic interpolated pseudo-particle method (CIP) for solving hyperbolic-type equations[J]. Journal of Computational Physics , 1985, 61 :261–268. doi:10.1016/0021-9991(85)90085-3 |
| [15] | YOKOI K. Efficient implementation of THINC scheme: A simple and practical smoothed VOF algorithm[J]. Journal of Computational Physics , 2007, 226 (2) :1985–2002. doi:10.1016/j.jcp.2007.06.020 |
| [16] | HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics , 1981, 39 (1) :201–225. doi:10.1016/0021-9991(81)90145-5 |
| [17] | PESKIN C S. Flow patterns around heart valves: a numerical study[J]. Journal of Computational Physics , 1972, 10 (2) :252–271. doi:10.1016/0021-9991(72)90065-4 |
| [18] | GRGGNHOW M, LIN W M. Nonlinear free-surface effects: experiments and theory[R]. MIT Report, Department of Ocean Engineering, Cambridge, USA, 1983: 83-119. |
 2016, Vol. 33
2016, Vol. 33