计算物理  2016, Vol. 33 Issue (1): 23-29
文章快速检索     高级检索
0
激波与火焰面相互作用数值模拟的GPU加速[PDF全文]
蒋华, 董刚, 陈霄     
南京理工大学瞬态物理重点实验室, 江苏 南京 210094
摘要: 为考察计算机图形处理器（GPU）在计算流体力学中的计算能力，采用基于CPU/GPU异构并行模式的方法对激波与火焰界面相互作用的典型可压缩反应流进行数值模拟，优化并行方案，考察不同网格精度对计算结果和计算加速性能的影响.结果表明，和传统的基于信息传递的MPI 8线程并行计算相比，GPU并行模拟结果与MPI并行模拟结果相同；两种计算方法的计算时间均随网格数量的增加呈线性增长趋势，但GPU的计算时间比MPI明显降低.当网格数量较小时（1.6×104），GPU计算得到的单个时间步长平均时间的加速比为8.6；随着网格数量的增加，GPU的加速比有所下降，但对较大规模的网格数量（4.2×106），GPU的加速比仍可达到5.9.基于GPU的异构并行加速算法为可压缩反应流的高分辨率大规模计算提供了较好的解决途径.
关键词: 激波     火焰界面     GPU     异构系统     加速比    
A Numerical Study of Interactions Between Shock Waves and Flame with GPU Acceleration
JIANG Hua, DONG Gang, CHEN Xiao     
Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Jiangsu Nanjing 210094, China
Abstract: To study performance of graphic processing unit (GPU) for computational fluid dynamics, simulation on interactions between shock waves and a flame interface, a typical compressible reactive flow, was carried out on CPU/GPU heterogeneous system. Several optimal strategies are taken to raise GPU code performance. Computational results and acceleration performance of GPU with different grid number were examined. It was found that computational results by parallel GPU are the same as those by traditional CPU based on MPI parallel of 8 threads. Computational times of two parallel methods linearly grow with increase of computational grid numbers. Compuational cost by GPU is less than cost by MPI. As grid number is small(1.6×104), speedup ratio of 8. 6 was achieved on GPU. As grid number grows, speedup ratio decreases. However, a ratio of 5.9 still can be held on GPU when grid number is more (4.2×106). Arithmetic on CPU/GPU heterogeneous system provides a good solution for large-scale computations of compressible reactive flows.
Key words: shock wave     flame interface     GPU     heterogeneous system     speedup ratio    
基金项目: 国家自然科学基金（11372140）和江苏省研究生科研创新计划（KYLX_0328）资助项目
作者简介: 蒋华(1988-),男,博士生,主要从事计算流体力学研究,E-mail:18951895841@126.com 董刚(1970-),男,博士,研究员,主要从事计算流体力学研究,E-mail:dgvehicle@yahoo.com
收稿日期: 2014-12-04; 修回日期: 2015-04-03
0 引言

GPU(Graphic Processing Unit，即“图形处理器”)在并行数据计算上具有的强大浮点运算能力，近年来吸引了越来越多的计算流体力学研究者的注意.CUDA(Compute Unified Device Architecture，2008年NVIDA公司发布)是一种基于并行编程模型和指令集的通用计算构架，支持使用C语言开发编程.基于CUDA的计算架构可以有效利用GPU强劲的运算能力和巨大的存储器带宽进行流体力学等数值计算，从而减少计算花费，提高计算效率.国外的一些研究者已经实现基于GPU的计算流体力学模拟和加速，如Elsen等[1]将GPU用在超音速飞行器流场的大规模计算中；Cohen[2]等用CUDA改写了计算流体力学代码，将其用在GPU计算中，获得了比高端CPU单线程最高8.5倍的加速比；Brandvik等[3]提出基于GPU加速的三维Navier-Stokes求解器来模拟涡轮机流场，GPU单卡获得了比CPU单线程最高19倍的加速比.近年来国内也开始了这方面的研究，如2011年董廷星等[4]将GPU应用到计算流体力学中的可压缩、不可压缩Navier-Stokes方程的计算中，相较于单核CPU，GPU平台获得了最高33.2倍的加速比；最近刘枫等[5]在CPU/GPU异构体系结构的计算集群上建立了基于MPI+CUDA的异构并行可压缩流求解器，并应用在高超声速流动的数值模拟中.

当前，主流的数值计算加速方法是CPU多线程并行计算，GPU只负责图形渲染.虽然GPU的浮点运算能力是同代的主流CPU的数十倍，但是其构架和CPU有本质的不同，因此，CPU上运行的模拟程序需要改变总体架构才能适应基于GPU的计算.目前基于GPU在分子动力学及计算流体力学等领域的算法研究主要考察的是GPU相对于CPU串行(单核)执行的加速比[2, 4, 6]，而相对于多核CPU并行执行的加速研究较少.基于消息传递的MPI并行是使用较多的CPU并行手段，分别基于MPI和GPU的并行方法到底各有什么优势，两者计算效率相较如何，目前此方面研究报道较少.本文以激波与预混火焰界面相互作用过程为算例，实现了分别基于消息传递的MPI并行加速和基于GPU并行加速的数值模拟，考察了不同计算网格分辨率下激波诱导火焰的失稳过程，分析了GPU的加速性能.

1 数理模型和算法实现 1.1 数理模型

激波与预混火焰界面的相互作用可以导致火焰界面出现Richtmyer-Meshkov(RM)不稳定现象，进而促进已燃气和未燃气的充分混合，导致燃烧加速[7-10]，这一过程涉及激波、稀疏波、接触间断(界面)以及化学反应等现象，是典型的可压缩反应流动过程，广泛出现在超燃推进[11]和工业爆炸灾害[12]等人类生产实践活动中.本文采用二维带化学反应的Navier-Stokes方程来描述该过程，控制方程

$\frac{\partial U}{\partial t}+\frac{\partial (F-{{F}_{D}})}{\partial x}+\frac{\partial (G-{{G}_{D}})}{\partial y}=S,$ (1)

其中

$U={{\left( \rho ,\rho u,\rho v,\rho E,\rho Y \right)}^{T}},$ (2)
$F={{(\rho u,\rho {{u}^{2}}+p,\rho uv,\left( \rho E+p \right)u,\rho uY)}^{T}},$ (3)
${{F}_{D}}={{(0,{{\tau }_{xx}},{{\tau }_{yy}},{{q}_{x}}+u{{\tau }_{xx}}+v{{\tau }_{xy}},D\rho \partial Y/\partial X)}^{T}},$ (4)
$G={{(\rho v,\rho vu,\rho {{v}^{2}}+p,\left( \rho E+p \right)v,\rho vY)}^{T}},$ (5)
${{G}_{D}}={{(0,{{\tau }_{y}}_{x},{{\tau }_{xx}},{{q}_{y}}+u{{\tau }_{yx}}+v{{\tau }_{yy}},D\rho \partial Y/\partial y)}^{T}},$ (6)
$S={{(0,0,0,0,\rho {{S}_{Y}})}^{T}},$ (7)

式中，ρ为密度； u和v为x和y方向的速度分量； p为压力； τij(i, j=x,y)为粘性应力张量； D为扩散系数； E为单位体积总能量，$E=p/(\gamma -1)+0.5\rho \sum\nolimits_{i=1}^{2}{{{u}_{i}}^{2}}+\rho qY$，γ为比热比； q为单位质量的总化学能； Y为反应物质量分数； qj(j=x，y)为热通量； SY为化学反应速率.控制方程采用分裂算法求解，其中，输运项FD，GD采用二阶中心差分格式计算；对流项F,G采用基于PPM(Piecewise Parabolic Method，分段抛物插值重构)的TVD格式[13]计算；化学反应源项S采用单步反应描述，其化学反应热力学和动力学参数的确定可参见文献[10]；时间推进过程采用了二阶Runge-Kutta方法.

1.2 并行模式和编程优化

基于消息传递的MPI并行是传统的CPU多线程并行模式，其基本思想是把计算区域划分为N个子区域，初始化各个子区域后，由N个CPU的线程分别对N个区域进行计算.由于此并行方法很常见，本文不再赘述.CPU适合进行判断、选择等复杂的计算任务，而GPU则对简单无分支的指令具有更强的计算能力，对于由CPU和GPU共同组成的异构系统，通常把CPU称为主机，把GPU称为设备.本文CUDA编程的CPU/GPU异构并行模式如图 1所示.此模式下，由主机完成数据初始化，然后将数据传入设备，GPU启动与网格数量等量的线程(例如需要对网格1 024×64的模型进行迭代计算，则启动1 024×64个线程来并行计算)完成密集型的大型迭代计算，每个时间步的数据仅在显存内更替，完成读取和存储.

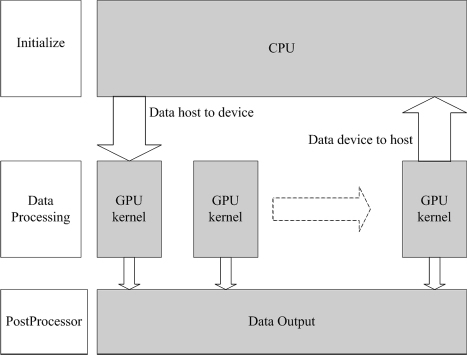图 1 CUDA并行计算模式示意图 Fig.1 Parallel computing model of CUDA

对于上节所述的数学模型，程序主要执行3项密集型计算：抛物重构(Reconstitution)，即对当前时间步网格边界两侧的解进行非线性(抛物形)构造，以提高计算精度；通量计算(Fluxes)，即对式(1) 中的F，FD，G，GD进行求解；化学反应(Reaction)，即对式(7) 中化学反应速率SY的求解.本文针对上述3项密集型计算任务的异构化编程流程如图 2所示.该流程主要包括：在主机端完成初始化、数据传输及文件写入等操作，设备端启动线程完成(虚线框中)抛物重构、通量计算和化学反应项的计算，主机端和设备端各自完成指定任务，在每个时间节点存在数据交换.

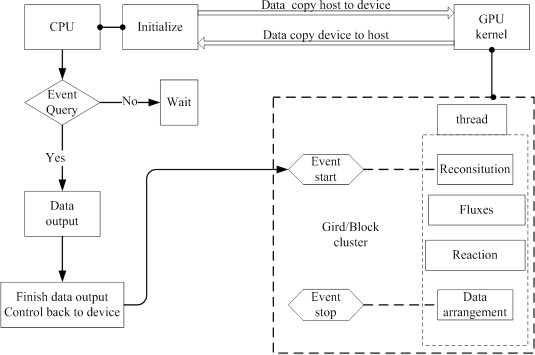图 2 CPU/GPU异构并行计算流程图 Fig.2 Flow chart of parallel computing on CPU/GPU heterogeneous system

在异构系统中，GPU线程执行的每个计算项之间需要交换的数据量很大，主设之间存在数据交换，线程与线程之间存在数据交换，如此多的数据传输和读取影响着系统性能，此外，由于主设分别执行任务，当设备处于计算和显存内部数据交换时，主机端处于闲置状态，等待空闲的时间开销很大.针对以上问题，本文采用了如下3种方法对程序进行优化：①利用CUDA的“事件”函数(Event)使主机和设备异步并发地执行任务.“事件”是CUDA提供的一种查询设备状态的函数(利用“事件”的起始和终止时间戳可以记录时间，精度0.1 ms，这也是本文测量GPU计算时间的方法).启动“事件”后，当设备处于运算状态时，会将状态反馈给主机，并将控制权返回给主机，主机就可以在设备工作的同时执行数据更新和文件写入等操作.实现主机端和设备端的异步并发，这样可以有效隐藏主机端的数据处理时间，降低主机端空闲时间.②使用GPU的常量存储器.程序在计算抛物重构、通量计算以及化学反应各项时，除了需要从主机端读入流场数据，还有很多常量数据需要读取，高频率的存取这些常量数据会占用带宽，降低GPU计算效率.将这些数据在程序初始化时就存入GPU的常量存储器中，可以节省带宽，加快访存速度.③额外开辟显存，存储每个时间步节点上需要更新的数据，减少主设数据交换次数和避免访存冲突.

2 模拟结果与计算性能分析

模拟激波与预混火焰界面相互作用的模型如图 3所示.

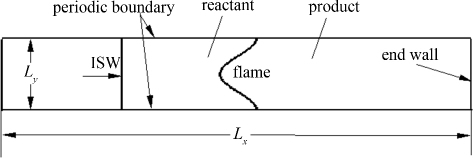图 3 二维模型流场示意图 Fig.3 Sketch of 2D numerical model

计算区域流向Lx为0.102 4 m，法向Ly为0.006 4 m；反应性预混气体(反应物)组成为C2H4+3O2+4N2，密度ρ0=0.161 5 kg·m-3，初温T0=293 K；初始火焰中心界面位于x=0.025 m，火焰区(产物)内密度ρ1=0.015 78 kg·m-3，火焰内外压力均为p0=13.3 kPa；入射激波马赫数1.3，初始时位于x=0.02 m处，激波沿x方向从左向右传播，当行至右端壁面后发生反射，左行的反射激波与火焰再次作用.初始预混火焰界面为余弦型界面，由于正交化网格带来的阶梯扰动会随着时间的发展逐渐放大，为了消除这种非物理扰动，采用扩散型界面来表示初始界面，具体方法参见文献[14]，这种扩散型火焰界面可在正交化网格中过渡光滑，更接近实际物理界面.计算区域上下边界采用周期条件，左端为速度入口条件，右端为无滑移固壁条件.采用均匀网格，由于GPU的执行模式是以线程块(block)中的32个线程为一个单位来启动执行指令的，计算核(SM)中如果这32个线程中出现分支，则这些线程将依次串行执行，这降低了指令吞吐量，影响计算速度，因此本文选用的网格数量都是32的倍数，这样分配线程时可以适当避免线程分支的出现.

在数值计算中，GPU并行采用448核Tesla C2075 GPU实现，而MPI并行则采用8核双路Intel Xeon CPU的8个线程来实现.

2.1 模拟结果分析

图 4给出了不同网格数量下，马赫数为1.3的入射激波及其反射激波分别与火焰界面作用后，流场的组分分布，其中浅色部分代表未燃气(重密度气体)，深色部分代表已燃气(轻密度气体).可以看出，入射激波和火焰界面相互作用后，由于火焰界面表面的密度梯度和激波压力梯度的方向不一致，产生斜压效应，进而在火焰界面形成涡量，使得火焰界面发生RM不稳定.此时界面左侧重气体(未燃气)会进入右侧轻气体(已燃气)中从而形成蘑菇状的“钉”(spike)结构[15]，如图 4(a)所示.当作用后的入射波(图中直线，箭头所指为激波运动方向)继续右行，到达右端界面后会发生反射.于是左行的反射激波会再次作用于火焰界面，此时火焰界面变形加剧，具体表现为“钉”结构沿流向进一步拉伸为细长形，如图 4(b)所示.需要指出的是，上述分布是采用GPU并行方案计算得到的结果，采用MPI并行计算得到的结果与图 4完全相同，这里不再给出，这也说明不同的算法对计算结果是没有影响的.

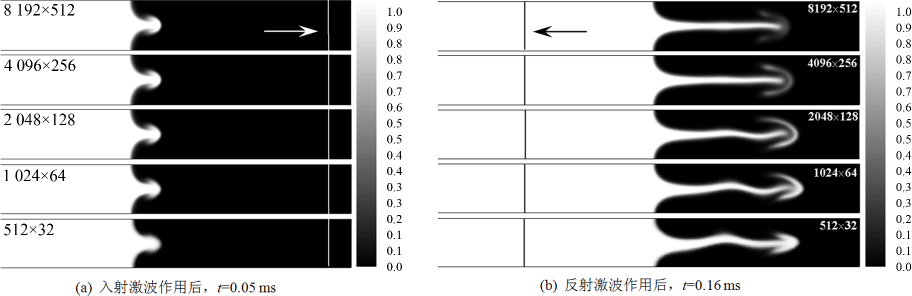图 4 不同网格精度下流场组分分布 Fig.4 Flow field constutent distribution with different grid precision

图 4的结果表明，反射激波作用前(图 4(a))，不同网格精度对界面变形影响不大；而反射激波作用后(图 4(b))，变形界面的“钉”结构随不同网格精度呈现出明显不同：当网格较粗时(如512×32) ，细长的钉结构沿流向呈现出波动.钉结构右端还出现了明显的蘑菇形状，随着网格加密，钉结构的波动形态逐渐消失，蘑菇形状也逐渐消失，钉结构出现平直的形态.图 5进一步给出了不同网格精度下激波管水平中心线上的密度分布，其结果也表明，随着网格精度的增加，计算结果逐渐趋于一致和稳定.

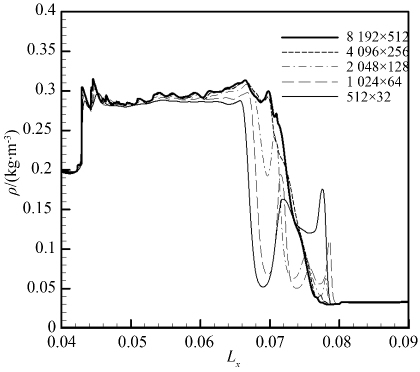图 5 不同网格精度下火焰中心位置流向密度分布图 Fig.5 Density distribution along stream on the flame middle position with different grid precision
2.2 计算效率分析

如前文所述，在激波与火焰面相互作用的数值模拟中，GPU执行的密集型计算主要是抛物重构、通量计算和化学反应计算.为了对比GPU和MPI两种并行方法的计算效率，图 6给出了两种并行方法平均单个时间步里上述各项耗费时间的对比.可以看出，对所有网格规模，MPI方法在通量计算项中耗时最多，而GPU方法在抛物重构项中耗时最多.在MPI并行模式下(图 6(a))，其并行是子区域之间的并行，每个子区域内部仍然是串行执行的，由于串行计算中通量计算总是最耗时的，因此，改变网格数量，子区域中各项计算耗费时间比例不变，总体各项时间比例也不会变.在GPU并行模式下(图 6(b))，密集型计算任务划分到每个GPU线程后，每个线程执行的计算任务很小，单个线程计算耗费时间总是固定的，此时，各项耗费时间主要受线程对显存的数据读取的影响.在本文中，抛物重构项在每个时间步里，线程对显存读取的网格参数数据量比通量计算和化学反应项都要大，读取次数也最多，因此抛物重构项耗费的时间最多.在图 6中无论是MPI并行还是GPU并行，由于化学反应项采用的是单步化学反应，其计算量总是最少的，然而对于GPU并行模式下的8 192×512网格规模，由于此时化学反应项数据读取的时间已经超过通量计算数据读取的时间，因此GPU在此项上耗费的时间反而超过通量计算耗费时间.

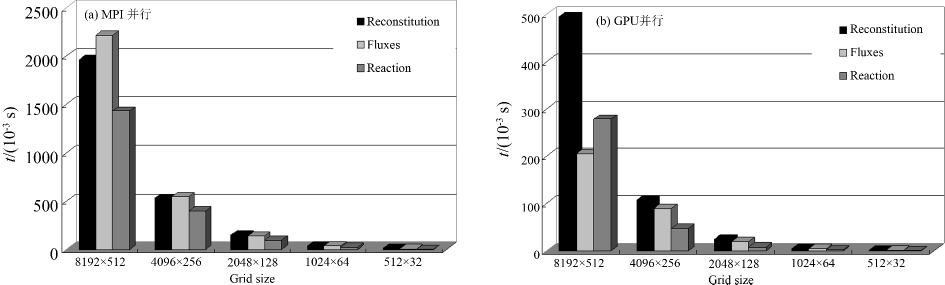图 6 单个时间步各项平均计算时间 Fig.6 Average computation time of each item on one time step

将各项的平均计算时间加和就可以得到单个时间步的平均计算时间，图 7给出了GPU和MPI并行单个时间步长计算时间和计算效率随网格规模变化的关系.可以发现，图 7中GPU和MPI方法的计算时间均随网格数量的增加呈线性增长趋势，这与文献[16]的结论是一致的.然而，GPU计算所需时间明显比8线程MPI并行要少很多.图 8给出了GPU方法相对于8线程MPI并行方法的加速比随网格规模变化的关系.可以发现，当网格数量较小时，GPU的加速比较高，最大可达8.7倍；随着网格数量的增加，加速比有所下降，但在本文网格数量最多的情况下，加速比仍可达到5.9.

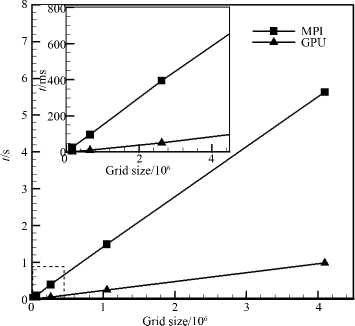图 7 不同网格规模下的单步平均时间 Fig.7 Everage step time with different grid precision

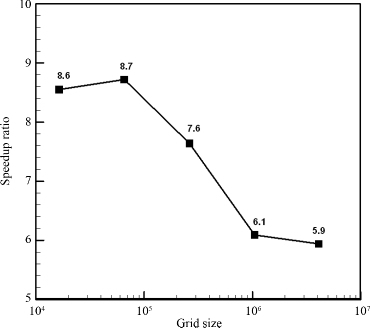图 8 不同网格规模下的加速比 Fig.8 Speedup ratio with different grid precision

图 8中随着网格规模的增加，GPU并行带来了加速比的下降，其主要原因是由于网格规模扩大，MPI并行模式的数据处理效率变高，子区域数据交换时间被有效隐藏；而GPU随着网格规模变大，线程从显存读取数据量变大，读取时间变长，而且线程块/线程数在显卡处理单元SM上对数据交换的隐藏效果不如CPU线程好，这些硬件差异使得MPI并行的效率能有所提高.尽管如此，对于更加接近真实结果的大规模网格而言(8 192×512，参见2.1节)，相对于8线程的MPI并行，5.9倍的加速比仍然体现了GPU并行的显著优势.

3 结论

使用基于GPU的异构系统模拟了不同网格规模下激波及其反射激波作用预混火焰界面的过程，通过CUDA中“事件”查询的方法实现了异步并发的执行模式，提高了并行效率，节约了时间成本，此外还使用了常量存储器等方法对程序作了进一步优化.模拟结果与传统的基于信息传递的MPI8核并行计算结果进行了对比.计算结果表明，两种方法得到的计算结果是一致的；网格规模越大，计算结果越趋于真实稳定.GPU线程计算时间稳定，当网格数量较少时，平均单个时间步获得了比8线程MPI并行最高8.7倍的加速比，当网格数量较多时，仍可达到5.9倍的加速比.测试结果显示了基于GPU的异构并行加速算法的优势和强大潜力.上述两种并行方式的比较和研究为基于计算流体力学的并行编程及优化提出了很好的解决途径，为多GPU、多主机的异构并行模式的大规模协同运算提供了一定的指导.

参考文献
[1] ELSEN E, LEGRESLY P, DARVE E. Large calculation of the flow over a hypersonic vehicle using a GPU[J]. Journal of Computational Physics , 2008, 227 (24) :10148–10161. doi:10.1016/j.jcp.2008.08.023
[2] CPHEN J M, MOLEMAKER M J. A fast double precision CFD code using CUDA[J]. Journal of the Physical Society of Japan , 2009, 1 (2) :237–341.
[3] BRANDVIK T, PULLAN G. An accelerated 3D Navier-Stokes solver for flows in turbomachines[J]. Journal of Turbomachinery , 2011, 133 (2) :021–025.
[4] DONG T X, LI X L, LI S, et al. Acceleration of computational fluid dynamics codes on GPU[J]. Computer Systems & Applications , 2011, 20 (1) :104–109.
[5] LIU Feng, LI Hua, TIAN Zhengyu, et al. Heterogeneous parallel compressible flow solver based on MPI+CUDA[J]. Journal of National University of Defense Technology , 2014, 36 (1) :6–10.
[6] HUANG Shuo, XIAO Jinyou, HU Yucai, et al. GPU-accelerated boundary element method for Burton-Miller equation in acoustics[J]. Chinese J Comput Phys , 2011, 28 (4) :481–487.
[7] KHOKHLOV A M, ORAN E S, CHTCHELKANOVA A Y, et al. Interaction of a shock with a sinusoidally perturbed flame[J]. Combustion and Flame , 1999, 117 (1-2) :99–116. doi:10.1016/S0010-2180(98)00090-X
[8] DONG G, JIN J M, YE J F, et al. A study of flame instability with wave propagation algorithm[J]. Chinese Journal of Computational Physics , 2005, 22 (4) :371–376.
[9] DONG G, FAN B C, YE J F. Numerical investigation of ethylene flame bubble instability induced by shock waves[J]. Shock Waves , 2008, 17 (6) :409–419. doi:10.1007/s00193-008-0124-3
[10] ZHU Yuejin, DONG Gang, FAN Baochun. Three-dimensional computation of the interactions between shock waves and flame in a confined space[J]. Journal of Propulsion Technology , 2012, 33 (3) :405–411.
[11] YANG J, KUBOTA T, ZUKOSKI E E. Applications of shock-induced mixing to supersonic combustion[J]. AIAA Journal , 1993, 31 (5) :854–862. doi:10.2514/3.11696
[12] ORAN E S, GAMEZO V N. Origins of the deflagration-to-detonation transition in gas-phase combustion[J]. Combustion and Flame , 2007, 148 (1) :4–47.
[13] CHAKRAVARTHY S R, OSHER S. A new class of high accuracy TVD schemes for hyperbolic conservation laws[J]. AIAA Paper , 1985, 85 :0363.
[14] JIANG Hua, DONG Gang, CHEN Xiao. Numerical study on the effects of small-amplitude initial perturbations on RM instability[J]. Chinese Journal of Theoretical and Applied Mechanics , 2014, 46 (4) :544–552.
[15] BROUILLETTE M. The Richtmyer-Meshkov instability[J]. Annual Review of Fluid Mechanics , 2002, 34 (34) :445–468.
[16] IMAN Gohari S M, ESFAHANIAN V, MOQTADERI H. Coalesced computations of the incompressible Navier-Stokes equations over an airfoil using graphics processing units[J]. Computer and Fluids , 2013, 80 (7) :102–115.
引用本文
蒋华, 董刚, 陈霄 . 激波与火焰面相互作用数值模拟的GPU加速[J]. 计算物理, 2016, 33(1): 23-29.
JIANG Hua, DONG Gang, CHEN Xiao . A Numerical Study of Interactions Between Shock Waves and Flame with GPU Acceleration[J]. CHINESE JOURNAL OF CONPUTATIONAL PHYSICS, 2016, 33(1): 23-29.