| SC混沌比例投影同步方法在保密通信中的应用 |
自1990年美国海军实验室的Pecora和Carroll第一次观察到混沌同步现象以来[1],关于混沌同步方法和混沌通信方案的研究在国际上兴起了二十多年.科研工作者相继提出了多种混沌同步的方法,主要有以下三种:一致性同步[2-3]、一般性同步[4]和相位同步[5].一般性同步和相位同步大多不应用于通信场合,因为通信领域需要保证载波信号再生的精确度.混沌一致性同步的方法主要包括驱动-响应式(主-从式)同步以及误差-反馈式同步两种.
混沌同步的研究是混沌安全保密通信的基础,混沌同步应用于保密通信的基本思路是,在发送端将传输信号隐藏在混沌载波(混沌信号)中,或者利用符号动力学以不同形状的波形表示对应的信息序列,而在接收端则通过混沌特性解调出传输的有用信息.从发送端的编码到接收端的解码,整个过程成功与否的关键在于通信收发双方的混沌同步.混沌信号具有非周期性、宽频带和类噪声的特点,外界一般会把隐藏或叠加在混沌信号中的信息信号误认为是噪声信号,所以很难被窃取.要想解调出发送的信息信号,只有掌握了通信双方的同步控制约定后方能做到,达成保密效果.
混沌掩盖、混沌调制、混沌键控和扩频通信是目前提出和发展的四种基于混沌同步的保密通信技术.混沌掩盖是以一种混沌信号作为载体,该信号具有和高斯白噪声相似的统计特性,将所要传输的信息信号进行遮掩或隐藏,在接收端通过混沌同步,恢复出有用信息[6].最近几年,利用各种混沌同步方法,国内外在混沌数字通信领域出现了很多重要的新进展和新尝试[7-15],如利用自适应控制混沌同步的保密通信方案[8]、基于SC混沌同步方法的保密通信方案[10]、基于超混沌系统[12]和长距离双向双信道光纤混沌保密通信[13]等等.
自混沌同步现象被发现以来,海内外学者做了很多深入的研究,多种不同类型的同步现象也相继被提出.Mainieri和Rehacek于1999年指出驱动和响应系统可以同步到一个尺度因子上[16],此种同步现象即为投影同步.2006年,Yu、Peng 和 Liu 根据线性系统稳定性准则,提出了一种新的实现混沌投影同步的方法(SC比例投影同步方法)[17],其不仅适用于三维耦合部分线性系统,同时也适用于高维甚至超混沌系统.只要配置于线性项中的雅克比矩阵A特征值均具有负实部,驱动系统和响应系统即可以达到投影同步.该方法中Lyapunov函数不需要构造,系统条件Lyapunov指数也不用去计算,雅克比矩阵A也可在较广范围内配置,方法灵活,所以此混沌投影同步方法简单而又有效.
本文充分利用SC比例投影同步方法的优点,构造了一种保密通信方案.在适当分离配置的混沌载波向量中的某一分量输出中,掩盖进所要传输的正弦信息,将其传输给响应系统,最后在接收端,传输的正弦信息经投影同步、解密过程被恢复出来.
在实际应用中的电路设备发射端,传统保密通信方案通常得到的是一个单项输出,而本文提出的方案不同于以往的传统方案,发射端得到的是一个向量输出,与其对应的是一组电缆传输,有用信息被掩盖进其中某一条电缆传输的混沌载波,而根据混沌系统的不同,这个包含有用信息的混沌载波分量输出可以有很多种选择,不易被第三方破解.本方案与文献[10]提出的基于SC混沌同步方法的通信方案相比,虽然二者传输的载波信号都是混沌状态变量通过线性与非线性函数的组合,其组合方式根据雅克比矩阵的配置有多种选择,不会被一个返回回路破解.但由于投影同步方法被应用到本方案中,混沌载波信号中新增加了用于比例投影同步的比例因子α,α为任意选取的非零常数,在上述构建非线性组合混沌载波基础上,增加了载波信号与解码信息表达式的不确定性和复杂度,等同于二次加密,这无疑进一步提高了保密通信的安全性和有效性.
1 基于线性系统稳定性准则的SC比例投影同步方法[17]考虑一个如下描述的混沌系统
| $\dot x = f\left( {x\left( t \right)} \right),$ | (1) |
其中x(t)∈Rn是混沌系统的n维状态向量,f:Rn→Rn定义了一个n维向量场.将函数f(x(t))分解
| $f\left( {x\left( t \right)} \right) = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} x\left( t \right) + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over h} \left( {x\left( t \right)} \right),$ | (2) |
其中函数${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }$x(t)是f(x(t))的线性部分,${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over h} }$(x(t))则是f(x(t))的非线性部分.然后将${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }$x(t)进行适当分离配置: ${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }$x(t)=Ax(t)+Ax(t).这里A是满秩的常数矩阵,且配置其所有特征值均具有负实部,Ax(t)则是线性函数${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }$x(t)的剩余部分.令函数g(x(t))=Ax(t),h(x(t))=Ax(t)+${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over h} }$(x(t)),则混沌系统(1) 作为驱动系统可被重新描述为
| $\dot x\left( t \right) = g\left( {x\left( t \right)} \right) + h\left( {x\left( t \right)} \right) = Ax\left( t \right) + h\left( {x\left( t \right)} \right),$ | (3) |
然后构造一个新的系统作为响应系统
| $\dot w\left( t \right) = g\left( {w\left( t \right)} \right) + h\left( {x\left( t \right)} \right)/\alpha = Aw\left( t \right) + h\left( {x\left( t \right)} \right)/\alpha ,$ | (4) |
其中w(t)∈Rn是所构造新系统的n维状态向量,α为比例因子.定义两个系统的同步误差为e(t)=x(t)/α-w(t),其解由如下的等式确定
| $\dot e\left( t \right) = \dot x\left( t \right)/\alpha - \dot w\left( t \right) = A\left( {x\left( t \right)/\alpha - w\left( t \right)} \right) = Ae\left( t \right),$ | (5) |
显然e(t)的零点即是系统的平衡点.由于雅克比矩阵A的所有特征值均具有负实部,根据线性系统的稳定性判定准则,同步误差系统(5) 在零点渐近稳定,即当t→∞,e(t)→0,此时驱动系统的状态向量x(t)和响应系统的状态向量w(t)按照指定比例α达到同步,即有
| $\mathop {\lim }\limits_{t \to \infty } \left\| {x/\alpha - w} \right\| \to 0,{\rm{A }}{x_i}/{w_i} = \alpha ,i = 1,2, \cdots ,n.$ | (6) |
利用SC比例投影同步方法对传输信息进行混沌掩盖.将驱动系统(3) 的非线性项输出的混沌信号h(x(t))经过信号放大器处理变为h(x(t))/α,并在其第j项hj(x(t))/α中直接加入所需传输的正弦信息im(t),得到混沌信号和有用信息叠加的混合驱动信号
| $\begin{array}{l} s\left( t \right) = h\left( {x\left( t \right)} \right)/\alpha + i\left( t \right) = \left[ \begin{array}{l} {s_1}\\ \vdots \\ {s_j}\\ \vdots \\ {s_n} \end{array} \right] = \\ \left[ \begin{array}{l} {h_1}\left( {x\left( t \right)} \right)/\alpha \\ \vdots \\ {h_j}\left( {x\left( t \right)} \right)/\alpha \\ \vdots \\ {h_n}\left( {x\left( t \right)} \right)/\alpha \end{array} \right] + \left[ \begin{array}{l} 0\\ \vdots \\ {i_m}\left( t \right)\\ \vdots \\ 0 \end{array} \right] = \left[ \begin{array}{l} {h_1}\left( {x\left( t \right)} \right)/\alpha \\ \vdots \\ {h_j}\left( {x\left( t \right)} \right)/\alpha + {i_m}\left( t \right)\\ \vdots \\ {h_n}\left( {x\left( t \right)} \right)/\alpha \end{array} \right] \end{array}$ | (7) |
其中s(t)∈Rn是经过加密的n维混沌信号向量,有用信息加密在任意一个分量sj(t)中,任何想破解信息的第三方很难得知有用信息到底被隐藏在哪一组混沌载波中,而且混沌载波经过比例放大(或缩小)的处理,比例因子是任意非零常数,常规的同步方法就更难以同步破解.
混合驱动信号s(t)通过信道传输到接收端,驱使响应系统与驱动系统达到比例投影同步.响应系统输出同步后的混沌信号h′(w(t))=h(αw(t))/α,用混合驱动信号s(t)直接减去同步后的混沌信号h′(w(t))就可以在接收端恢复出传输的有用信息${\hat i}$m(t).正弦信号的加密解密过程如图 1所示.
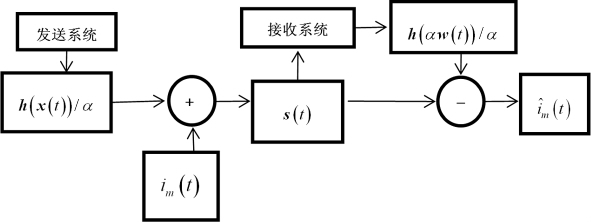 |
| 图 1 比例投影同步方法混沌掩盖加密解密过程示意图 Fig.1 Encryption and decryption process of chaotic masking |
接收端受混沌驱动信号驱使的微分方程为 ${\dot w}$(t)=Ax(t)+s(t),
| $\dot w\left( t \right) = Ax\left( t \right) + s\left( t \right),$ | (8) |
经还原后的解码信息为
| ${{\hat i}^m}(t) = s(t) - h{\rm{'}}(w(t)) = s(t) - h(\alpha w(t))/\alpha .$ | (9) |
根据上述分析,混沌驱动信号s(t)是原驱动系统非线性项经过一个任意常数的比例放大(或缩小)得到的,相较于以往传输信号是状态变量的线性组合而言,其使加密的有用信息的解密过程变得更为复杂,更难被破解,安全性得到了提高.
3 数值仿真 3.1 Lorenz吸引子Lorenz混沌系统可如下描述
| $\begin{array}{l} {{\dot x}_1} = \sigma ({x_2} - {x_1}),\\ {{\dot x}_2} = - {x_1}{x_3} + \gamma {x_1} - {x_2},\\ {{\dot x}_3} = {x_1}{x_2} - b{x_3}, \end{array}$ | (10) |
其中,σ=16,γ=45.92,b=4.将方程(10) 等号右端函数按照(3) 式进行适当分离,配制出函数g(x(t))和h(x(t)),
| $\begin{array}{l} g\left( {x\left( t \right)} \right) = A\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - \sigma } & {} & {}\\ {} & { - 1} & {}\\ {} & {} & { - b} \end{array}} \right]\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3} \end{array} \right],{\rm{ }}\\ h\left( {x\left( t \right)} \right) = \left[ \begin{array}{l} \sigma {x_2}\\ - {x_1}{x_3} + \gamma {x_1}\\ {x_1}{x_2} \end{array} \right], \end{array}$ | (11) |
雅克比矩阵A为对角阵,是最简单的一种配置,其三个特征值是(-16,-1,-4) ,均为负实数.取正弦信息im(t)=asin(ωt).首先将传输信息im(t)加入到非线性传输信号h(x(t))/α中的第一项h1(x(t))/α中去,构造发送端混合驱动信号
| $s\left( t \right) = \left[ \begin{array}{l} \sigma {x_2}/\alpha \\ \left( { - {x_1}{x_3} + \gamma {x_1}} \right)/\alpha \\ {x_1}{x_2}/\alpha \end{array} \right] + \left[ \begin{array}{l} {i_m}\left( t \right)\\ 0\\ 0 \end{array} \right].$ | (12) |
构造混沌掩盖通信系统接收端
| ${{\dot w}_1} = - \sigma {w_1} + {s_1}\left( t \right),{{\dot w}_2} = - {w_2} + {s_2}\left( t \right),{{\dot w}_3} = - b{w_3} + {s_3}\left( t \right);$ | (13) |
则接收端解码信息表达式为
| $\begin{array}{*{20}{l}} {{{\dot w}_2} = - {w_2} + {s_2}\left( t \right),}\\ {{{\hat i}^{(1)}}_m\left( t \right) = {s_1}\left( t \right) - {h_1}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) + \sigma {e_2}.} \end{array}$ | (14) |
若将传输信息分别加入到非线性传输信号h(x(t))/α中的第二项h2( x(t))/α和第三项h3(x(t))/α中,则在接收端解码信息表达式为
| $\begin{array}{l} {{\hat i}^{(2)}}_m\left( t \right) = {s_2}\left( t \right) - {h_2}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) - {x_1}{x_3}/\alpha + \alpha {w_1}{w_3} + \gamma {e_1},\\ {{\hat i}^{(3)}}_m\left( t \right) = {s_3}\left( t \right) - {h_3}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) + {x_1}{x_2}/\alpha - \alpha {w_1}{w_2}. \end{array}$ | (15) |
根据式(5) 、(12) 同步误差的微分方程是
| $\left[ \begin{array}{l} {{\dot e}_1}\\ {{\dot e}_2}\\ {{\dot e}_3} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - \sigma } & {} & {}\\ {} & { - 1} & {}\\ {} & {} & { - b} \end{array}} \right]\left[ \begin{array}{l} {e_1}\\ {e_2}\\ {e_3} \end{array} \right] = A\left[ \begin{array}{l} {e_1} + {i_m}\left( t \right)\\ {e_2}\\ {e_3} \end{array} \right].$ | (16) |
由于雅克比矩阵A的所有特征值均具有负实部,依据线性系统的稳定性准则判断,驱动系统和响应系统的同步误差具有渐近稳定性.
初始值令x0=[8.0,5.5,3.5]T,w0=[3.0,2.0,1.5]T,文中采用正弦信息im(t)=asinωt作为传输的有用信息,取a=15,ω=0.5,指定一个比例因子α=0.5,利用四阶Runge-kutta方法数值模拟,图 2是利用混沌掩盖技术对正弦信息进行加密解密的结果.图 2(a)显示了状态变量w和x/α的投影同步误差e1(t),e2(t),e3(t)随时间发展变化趋势,从图中可以看出,e2(t)和e3(t)随时间迅速收敛到0,而e1(t)在时间域中是一条三角函数曲线,并不收敛.出现上述情况的原因是正弦信号im(t)具有较大的振幅a=15,当其被掩盖进混沌载波信号s(t)的第一个分量s1(t)中,破坏了w1和x1/α的投影同步结果.但根据解码信息im(t)的表达式(14) ,式中并不包含w1和x1/α,因此信息信号的解密恢复不受影响.图 2(b)显示了传输的混合驱动信号s(t)的第一分量s1(t)随时间的发展变化,可以看出s1(t)是混沌信号,正弦信息被很好地隐藏,加密成功.图 2(c)显示的是传输的正弦信息信号im(t)与在接收端被还原出的解码信息信号${\hat i}$m(t),可以发现还原信号经过一个短暂的瞬态过程后收敛到原始信息信号,此后保持稳定.图 2(d)显示的是把正弦信号分别加到s(t)的三个分量中,在接收端解码信息与所传输正弦信息的同步误差时间历程图.可以发现当正弦信息加入到混沌载波信号第二分量s2(t)时,解码信息${\hat i}$m(t)的收敛时间最短,而加入到其它两个分量s1(t)和s3(t)中收敛时间一样,因此在不影响解码精度的情况下,将正弦信息加入到载波信号第二分量中是最优的.
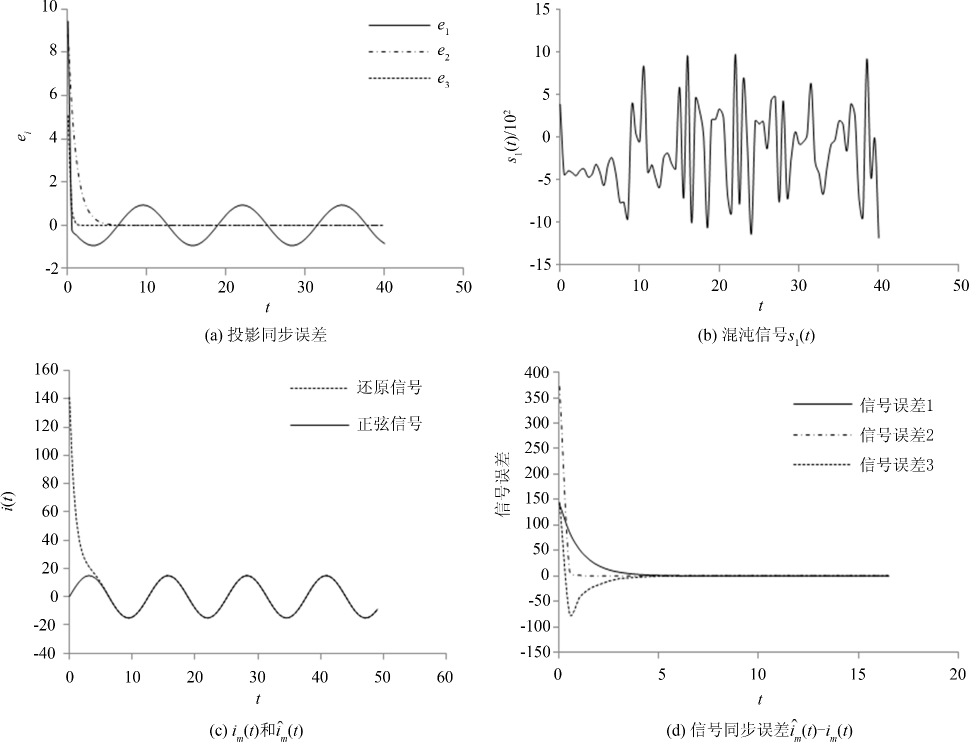 |
| 图 2 Lorenz系统的混沌掩盖 Fig.2 Chaotic masking with Lorenz system |
由式(16) 可以发现,系统3个同步误差方程相互独立,即当一组状态变量wj和xj/α因加入的正弦信息信号而投影同步失效时,其余两组状态变量的投影同步不受影响.从式(12) 可以看出,混沌载波信号s(t)的3个分量sj(t)中都不包含相应未实现比例投影同步的wj和xj/α,所以不论把所要传输的正弦信息信号加入到哪一个传输信号中,都不会影响接收端还原信息的收敛性和精度.
将正弦信号的振幅a、频率ω和比例因子α作为控制参数,取a∈[0.001,1 000],ω∈[0.01,100],α∈[-1 000,1 000],对上述加密解密过程进行数值模拟分析,发现解码的收敛性和精度不变,信号同步误差图与图 2(d)一致.说明不管是高频或低频、振幅大或小的正弦信息信号,都可以作为传输信号用上述混沌掩盖方式进行加密解密,且比例因子的选择范围也很大,使混沌载波信号更为复杂,增加了解码的困难程度.
接下来改变雅克比矩阵A的配置,使得混沌驱动信号s(t)中的第j项中含有xj,由于状态变量wj和xj/α受正弦信号振幅的影响而无法达到比例投影同步,则原始正弦信号就不会在接收端被还原出来.配置雅克比矩阵A=
| $s\left( t \right) = \left[ \begin{array}{l} (\sigma {x_2} + \beta {x_1})/\alpha \\ - {x_1}{x_3}/\alpha \\ {x_1}{x_2}/\alpha \end{array} \right] + \left[ \begin{array}{l} {i_m}\left( t \right)\\ 0\\ 0 \end{array} \right].$ | (17) |
还原信息表达式为
| ${{\hat i}_m}\left( t \right) = {s_1}\left( t \right) - \sigma \alpha {w_2} + \beta \alpha {w_1}/\alpha = {i_m}\left( t \right) + \sigma {e_2} + \beta {e_1},$ | (18) |
w1和x1/α无法实现比例投影同步,则式(18) 表示的${\hat i}$m(t)和im(t)也是不同步的,正弦信息解码失败.
考虑矩阵A的另一种配置,使其下三角元素均为0,
| $A = \left[ {\begin{array}{*{20}{c}} { - \sigma } & \sigma & {}\\ {} & { - 1} & \gamma \\ {} & {} & { - b} \end{array}} \right],{\rm{ }}h\left( {x\left( t \right)} \right)/\alpha = \left[ \begin{array}{l} 0\\ \left( { - {x_1}{x_3} + \gamma {x_1} - \gamma {x_3}} \right)/\alpha \\ {x_1}{x_2}/\alpha \end{array} \right],$ | (19) |
矩阵A的特征值为(-16,-4,-1) ,均为负实数.仍然取传输信息im(t)=asin(ωt),其中a=15,ω=0.5,加入到驱动信号的第二分量中得到混沌驱动信号
| $s\left( t \right) = \left[ \begin{array}{l} 0\\ \left( { - {x_1}{x_3} + \gamma {x_1} - \gamma {x_3}} \right)/\alpha \\ {x_1}{x_2}/\alpha \end{array} \right] + \left[ \begin{array}{l} 0\\ {i_m}\left( t \right)\\ 0 \end{array} \right],$ | (20) |
则解码信息表达式为
| $\begin{array}{l} {{\hat i}_m}\left( t \right) = {s_2}\left( t \right) - {h_2}\left( {\alpha w\left( t \right)} \right)/\alpha = \\ {i_m}\left( t \right) - {x_1}{x_3}/\alpha + \alpha {w_1}{w_3} + \gamma {e_1} - \gamma {e_3}. \end{array}$ | (21) |
图 3显示了矩阵A配置下正弦信号的加密解密结果.图 3(a)为状态变量w和x/α的投影同步误差历程图,从图中可以看出e1(t)和e2(t)在时间域中是两条完全重合在一起的三角函数曲线,没有收敛性,而e3(t)迅速收敛到0,并一直保持稳定.图 3(b)是在接收端还原出的信息信号,图像毫无规律可言,与原始正弦信息信号差别甚远.因为${\hat e}$1=-σe1+σe2,而正弦信息im(t)振幅较大破坏了w2和x2/α的投影同步,从而导致e2不收敛,所以e1也不收敛,因此变量w1和x1/α也不同步.${\hat e}$3=-be3,e3收敛为0.式(21) 中包含不同步的状态变量w1和x1/α,所以原始正弦信息无法在接收端被恢复出来.
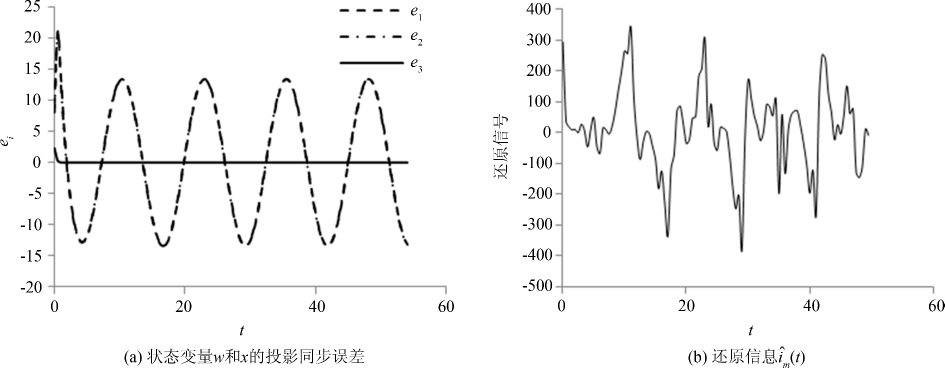 |
| 图 3 A为非对角型矩阵情况下的信息解密 Fig.3 Numerical simulation in the case of non-diagonal matrix A |
再考虑将雅克比矩阵配置为上三角元素均为0,如A=
| $s\left( t \right) = \left[ \begin{array}{l} \sigma {x_2}/\alpha \\ - {x_1}{x_3}/\alpha \\ {x_1}{x_2} \end{array} \right] + \left[ \begin{array}{l} 0\\ {i_m}\left( t \right)\\ 0 \end{array} \right];$ | (22) |
接收端恢复信息表达式为
| ${{\hat i}_m}\left( t \right) = {s_2}\left( t \right) - {h_2}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) - {x_1}{x_3}/\alpha + \alpha {w_1}{w_3}.$ | (23) |
因为恢复信息中不含有不同步的状态变量w2和x2/α,所以正弦信息信号im(t)可以在接收端被精确地还原出来.
由以上分析可知,Lorenz混沌系统最优的雅克比矩阵配置为对角型矩阵.因为当其矩阵配置为最简单的对角型时,混沌载波信号s(t)的3个分量sj(t)中不包含状态变量xj,从而接收端能够精确还原出解码信息.
3.2 超混沌Rössler吸引子超混沌Rössler吸引子的微分方程
| $\begin{array}{l} {{\dot x}_1} = - ({x_2} + {x_3}),{\rm{ }}{{\dot x}_2} = {x_1} + a{x_2} + {x_4},\\ {\rm{ }}{{\dot x}_3} = b + {x_1}{x_3},{\rm{ }}{x_4} = c{x_4} - d{x_3}, \end{array}$ | (24) |
选取参数a=0.25,b=3.0,c=0.05,d=0.5,在此参数下该方程有2个正Lyapunov指数λ1=0.16,λ2=0.03.将该系统进行适当分离配置得到
| $\begin{array}{l} g\left( {x\left( t \right)} \right) = A\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - 1} & \eta & {} & {}\\ 2 & { - 4} & {} & {}\\ {} & {} & { - 1} & {}\\ {} & {} & {} & { - c} \end{array}} \right]\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right],\\ h\left( {x\left( t \right)} \right) = \left[ \begin{array}{l} - \left( {\eta + 1} \right){x_3}\\ - {x_1} + \left( {4 + a} \right){x_2} + {x_4}\\ {x_3} + {x_1}{x_3} + b\\ 2c{x_4} - d{x_3} \end{array} \right], \end{array}$ | (25) |
其中η是一个可调参量且η可以为任意常数.不论η取何值,矩阵A的特征值都是-0.59,-3.41,-1,-0.05,均为负实数.取正弦信息im(t)=10sin(2t)加入到非线性信号h1(x(t))/α中得到混合驱动信号
| $s\left( t \right) = \left[ \begin{array}{l} - \left( {\eta + 1} \right){x_3}/\alpha \\ \left( { - {x_1} + \left( {4 + a} \right){x_2} + {x_4}} \right)/\alpha \\ \left( {{x_3} + {x_1}{x_3} + b} \right)/\alpha \\ \left( {2c{x_4} - d{x_3}} \right)/\alpha \end{array} \right] + \left[ \begin{array}{l} {i_m}\left( t \right)\\ 0\\ 0\\ 0 \end{array} \right]$ | (26) |
则接收端解码信息为
| ${{\hat i}_m}\left( t \right) = {s_1}\left( t \right) - {h_1}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) - \left( {\eta + 1} \right){e_3},$ | (27) |
因为${\hat i}$m(t)中不包含w1和x1项,所以是高精度解码信息.
取η=0,α=0.5,图 4(a)显示的是发送端系统和接收端系统各状态变量同步误差时间历程图.从图中可以看出,e1(t),e2(t)经过短暂的瞬态变化后是两条稳定的正弦曲线,而e3(t)很快收敛到0,e4(t)经过一段较长时间后也最终收敛到0.同步误差方程有${\hat e}$1=-e2+10sin2t,e·2=2e1-4e2,方程中存在正弦函数项,所以误差方程的解e1,e2与正弦函数具有相同的振荡频率,但振幅有所差别.
令η=0,α=0.5不变,将正弦信号的振幅a与频率ω作为控制参数,分别取a=20,10,5,1和ω=4,2,1,0.5对加密解密过程进行数值模拟分析,图 4(b)显示的是正弦信息取a=10,ω=0.5和a=1,ω=2时,所传输的混沌信号s1(t)时间历程图,可以发现正弦信息信号im(t)被很好地隐藏在混沌信号中,加密成功.图 4(c)显示了取不同振幅和频率时解码信息与正弦信息的误差时间历程图,由式(27) 得Δi(t)=${\hat i}$m(t)-im(t)=-(η+1) e3,Δi(t)在图中经过很短的瞬态过程后收敛为0,且Δi(t)在不同情况下的变化曲线均一致,因此解码的速度和精度不受正弦信号振幅与频率的影响.
图 4(d)显示当α=0.5,im(t)=10sin(2t),η取4组不同的数值η=-5,-0.5,0,5时,解码信息和正弦信息随时间发展图.图中可以看出解码信息曲线均经过一段相同的很短的时间过程后收敛至正弦信息曲线,说明控制矩阵A配置的可调参量η不仅增加了解码的复杂度,而且对解码的速度和精度不产生影响,因此可以用η作为控制器进行再一次加密.图 4(e)显示当η=0,im(t)=10sin(2t),比例因子α取4组不同的数值α=-1,0.5,2,10时,解码信息和正弦信息随时间发展图.从图中可得知比例因子α的选择不会对解码的收敛性和精度产生影响,因此α选取的任意性无疑增大了解码的困难程度.
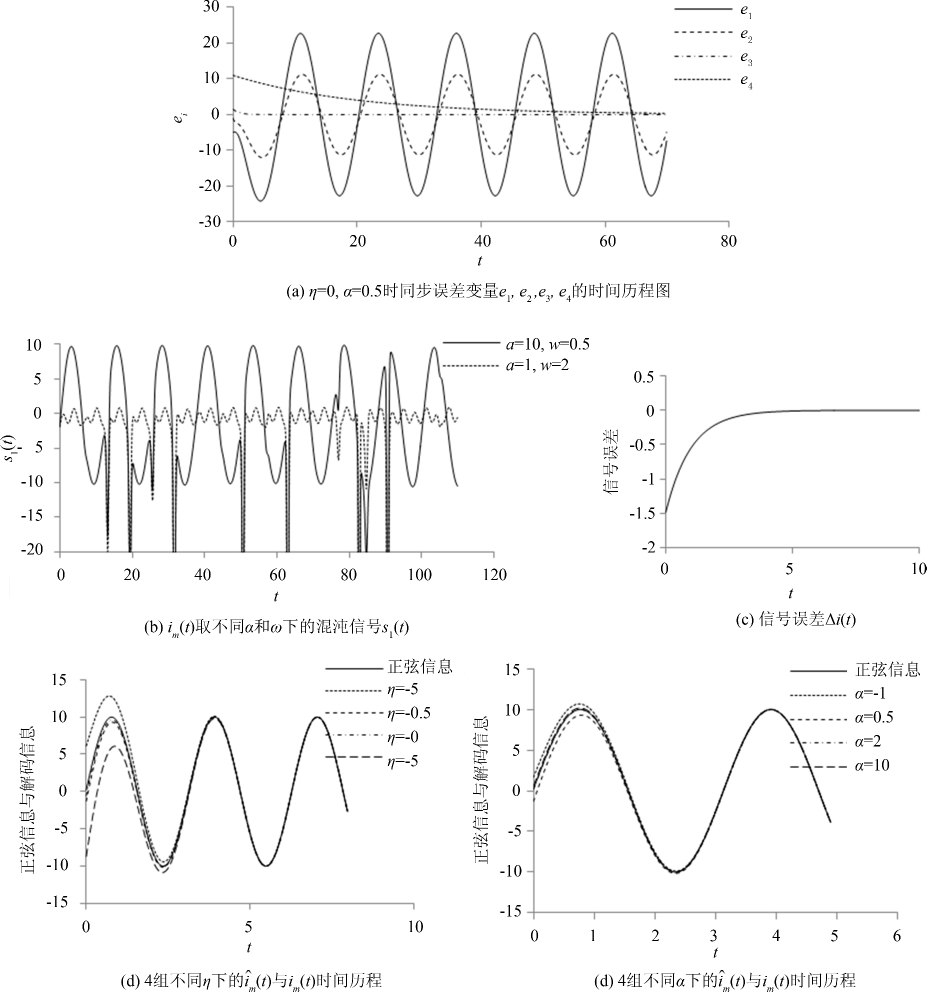 |
| 图 4 超混沌Rössler系统的混沌掩盖 Fig.4 Chaotic masking with hyper-chaoticRösslersystem |
接下来考虑超混沌Rössler系统的对角型雅克比矩阵的配置
| $\begin{array}{l} g\left( {x\left( t \right)} \right) = A\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - 1} & {} & {} & {}\\ {} & { - a} & {} & {}\\ {} & {} & { - 1} & {}\\ {} & {} & {} & { - c} \end{array}} \right]\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right],\\ {\rm{ }}h\left( {x\left( t \right)} \right) = \left[ \begin{array}{l} {x_1} - {x_2} - {x_3}\\ {x_1} + 2a{x_2} + {x_4}\\ {x_3} + {x_1}{x_3} + b\\ 2c{x_4} - d{x_3} \end{array} \right]. \end{array}$ | (28) |
雅克比矩阵A的特征值均为负实数.取所要传输的正弦信息im(t)=15sin0.5t加入到非线性信号h1(x(t))/α中得到混合驱动信号
| $s\left( t \right) = \left[ \begin{array}{l} \left( {{x_1} - {x_2} - {x_3}} \right)/\alpha \\ \left( {{x_1} + 2a{x_2} + {x_4}} \right)/\alpha \\ \left( {{x_3} + {x_1}{x_3} + b} \right)/\alpha \\ \left( {2c{x_4} - d{x_3}} \right)/\alpha \end{array} \right] + \left[ \begin{array}{l} {i_m}\left( t \right)\\ 0\\ 0\\ 0 \end{array} \right];$ | (29) |
构造接收端系统
| $\begin{array}{l} {{\dot w}_1} = - {w_1} + {s_1}\left( t \right),{\rm{ }}{{\dot w}_2} = - a{w_2} + {s_2}\left( t \right),{\rm{ }}\\ {{\dot w}_3} = - {w_3} + {s_3}\left( t \right),{\rm{ }}{{\dot w}_4} = - c{w_4} + {s_4}\left( t \right); \end{array}$ | (30) |
则接收端解码信息表达式为
| ${{\hat i}^{(1)}}_m\left( t \right) = {s_1}\left( t \right) - {h_1}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) + {e_1} - {e_2} - {e_3}.$ | (31) |
若将传输信息im(t)分别加入到非线性传输信号h(x(t))的第2项、第3项和第4项中,得接收端解码信息表达式为
| ${{\hat i}^{(2)}}_m\left( t \right) = {s_2}\left( t \right) - {h_2}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) + {e_1} + 2a{e_2} + {e_4},$ | (32) |
| $\begin{array}{l} {{\hat i}^{(3)}}_m\left( t \right) = {s_3}\left( t \right) - {h_3}\left( {\alpha w\left( t \right)} \right)/\alpha = \\ {i_m}\left( t \right) + {e_3} + {x_1}{x_3}/\alpha - \alpha {w_1}{w_3}, \end{array}$ | (33) |
| ${{\hat i}^{(4)}}_m\left( t \right) = {s_4}\left( t \right) - {h_4}\left( {\alpha w\left( t \right)} \right)/\alpha = {i_m}\left( t \right) + 2c{e_4} - d{e_3}.$ | (34) |
由于s(t)的每一分量中都包含相应的状态变量xj,所以解码信息${\hat i}$m(1) (t),i^m(2) (t),i^m(3) (t),i^m(4) (t)都不能够收敛到正弦信息im(t).取初始值x=[-5,-2,1,10.5]T,w=[-5,-3,0.5,10]T,令比例因子α=0.5,对正弦信号加密解密过程进行数值模拟.发现接收端并没有还原出原始正弦信号.当超混沌Rössler方程的雅克比矩阵A为对角阵时,混沌驱动信号s(t)中的第j项都含有xj,所以无论传输的正弦信号被掩盖进混沌载波信号的哪一分量中,接收端都会因为系统相应变量无法达到比例投影同步而不能精确还原出正弦信号im(t).
4 结论将一种基于线性系统稳定性准则的SC混沌投影同步方法应用到保密通信领域,对所要传输的正弦信息进行混沌掩盖,并精确地将其还原.以Lorenz吸引子和超混沌Rössler吸引子为例,对正弦信息信号的加密解密过程进行了数值模拟分析.在传输信息时注意选择合适的雅克比矩阵,使不同步的状态变量不包含于掩盖信息的混沌载波信号中,从而确保正弦信息在接收端能被精确还原.Lorenz系统最优的雅克比矩阵配置是对角型矩阵,而超混沌Rössler系统的矩阵采用对角型矩阵时,非线性传输信号的每个分量hi(x(t))/α都包含状态变量xi,因此在接收端总无法精确还原出解码信息.Lorenz系统和超混沌Rössler系统均可在较大范围内选取正弦信号的振幅和频率,在超混沌Rössler吸引子的雅克比矩阵A中还可使用可调参量η进行再一次加密.利用基于线性系统稳定性准则的混沌投影同步方法进行保密通信,相较于其它方案的优点,在于混沌载波信号里新加入了一个比例因子α,α为任意非零常数,这无疑使混沌载波信号更为复杂,不仅想要破解信息的第三方很难猜测出α的数值,而且加大了接收端解码信息的复杂程度,从而大大提高了保密通信的安全性.
| [1] | PECORA L M, CORROLL T L. Synchronization in chaotic systems[J]. Phys Rev Lett , 1990, 64 :821–824. doi:10.1103/PhysRevLett.64.821 |
| [2] | YU H J, Peng J H. Synchronization of nonlinear coupled hyper-chaotic Rössler systems and networks[J]. Chinese Journal of Computational Physics , 2006, 23 (05) :626–629. |
| [3] | YU H J, ZHEN N. Chaotic synchronization of networks of Chen's chaotic attractors using nonlinear coupling function[J]. Acta Phys Sin , 2008, 57 (08) :4713–4719. |
| [4] | KOCAREV L, PARLITZ U, PANOVSKI L. Generalized synchronization of chaos[J]. Circuits and Systems , 1996, 3 :116–119. |
| [5] | SHALFEEV V D, MATROSOV V V, KORZINOVA M V. Chaos synchronization in coupled phase systems[J]. Circuits and Systems , 1998, 4 :580–582. |
| [6] | LIU J J, ZHANG Y L. The application of chaotic masking and chaotic switching in secure communication[J]. IEEE , 2011, 16 :7781–7784. |
| [7] | PAN J, DING Q. The research of optimization based on Lorenz chaotic masking secure communication[J]. IEEE , 2010, 43 :1136–1139. |
| [8] | CHEN Q S, YANG L N. Chaos synchronization of secure communication based on adaptive inverse control[J]. IEEE , 2011, 32 :525–527. |
| [9] | PAN J, DING Q. The frequency truncation method research of Lorenz-based chaotic masking secure communication[J]. IEEE , 2011, 28 :174–178. |
| [10] | SONG Z P, YU H J. A technical scheme of secure communication based on SC chaotic synchronization method[J]. Science & Technology Review , 2011, 29 (23) :50–53. |
| [11] | GALINA C, ELENA D. Chaotic masking approach based on the doffing oscillator[J]. IEEE , 2012, 5 :42–45. |
| [12] | LIAO N H, HU Z H. A hybrid secure communication method based on synchronization of hyper-chaos systems[J]. IEEE , 2012, 12 :289–292. |
| [13] | ZHAO Y M, XIA G L, WU J G, WU Z M. Investigation of bidirectional dual-channel long-distance chaos secure communication based on 1550nm vertical-cavity surface-emitting lasers[J]. Acta Phys Sin , 2013, 62 (21) :1–6. |
| [14] | AROMATARIS G, ANNOVAZZI V. Enhancing privacy of chaotic communications by double masking[J]. IEEE , 2013, 18 :955–959. |
| [15] | ALPANA P, SHIKHA D. Secure communication using a modified chaotic masking scheme employing sprott94 case a chaotic attractor[J]. IEEE , 2014, 9 :1–6. |
| [16] | MANIERI R, REHACEK J. Projective synchronization in three-dimensional chaotic system[J]. Phys Rev Lett , 1999, 82 :3042–3045. doi:10.1103/PhysRevLett.82.3042 |
| [17] | YU H J, PENG J H, LIU Y Z. Projective synchronization of unidentical chaotic systems based on stability criterion[J]. Int J Bifur Chaos , 2006, 16 :1049–1052. doi:10.1142/S0218127406015301 |
 2016, Vol. 33
2016, Vol. 33

